基于超弹性本构模型的前悬架橡胶支座的静态特性研究

潘宇倩，覃朝兵

（1.柳州工学院机械工程系，柳州 545616； 2.柳州元吉兴工业技术有限公司，柳州 545616）

引言

橡胶是一种高分子材料，其高弹特性有不可取代的地位，可利用特有的粘弹性消耗能量。其广泛用于汽车隔振器，如动力总成悬置、扭转减振器、弹性联轴器、动力吸振器等[1]。典型的橡胶材料的应力—应变行为是弹性的，但又是高度非线性的。在分析橡胶材料的这种非线性时，通常使用超弹性本构模型来逼近。

目前用于橡胶隔振器的力-位移的本构模型较多：Mooney-Rivlin模型、Ogden模型、Neo-Hookean模型、Yeoh模型等。Seibert以Arruda-Boyce模型、Van Der Waals模型、Yeoh模型研究了橡胶本构模型的区别[2]。何小静等通过测试橡胶试片的应力应变关系，对比了不同橡胶超弹本构模型的差异，并在橡胶悬置上进行了验证[3]。王文涛等应用最小二乘法识别了常见的橡胶超弹本构模型的参数，比较了不同模型间的拟合精度[4]。Hartman提出了一种新的获取橡胶本构模型参数的方法，并通过试验进行了验证[5]。

汽车上的橡胶隔振器一般是橡胶与金属硫化而成，可承受较大冲击，并对高频振动有较好的吸收，从而达到隔振效果。车辆运行时，橡胶隔振器一般承受多向载荷。Wang等通过有限元研究了Mooney-Rivlin模型和Ogden模型的静态力-位移特性[6]。王伟利用有限元计算了橡胶减振器的轴向、径向、扭转力等[7]。郭孔辉等通过三项耦合的弹簧阻尼系统来简化橡胶衬套的弹性耦合，并在整车仿真中应用[8]。

本文选取集中超弹性本构模型对汽车前悬架橡胶支座的力-位移关系进行研究分析，通过不同硬度的的橡胶材料试片来提取橡胶超弹性本构模型参数，将拟合的本构模型参数赋予到支座的有限元模型中，求解其力-位移关系，并与测试结果进行对比。

1 橡胶本构模型

描述橡胶材料力学性能的基本方法：通过实验确定橡胶材料的应力应变属性，通过本构模型的拟合得到有关参数，通过有限元方法预测橡胶隔振器的静态特性。主要的实验有单轴拉伸、单轴压、平面剪切[9]。

一般采用应变势能来表达橡胶超弹性的应力—应变关系，有几种不同的应变势能：多项式模型、Ogden模型、Arruda-Boyce模型、Marlow模型和Van der Waals模型。多项式的简单模型有Mooney-Rivlin模型、Neo-Hookean模型、简单多项式模型和Yeoh模型。

应变能势函数U的一般形式为[10]：

式中：

I1，I2，J— 一阶、二阶、三阶不变量；

C1，C2，…，Cm—m个超弹性材料剪切特性的常数；

d1，d2，…，dm—m个超言行材料压缩特性的常数。

I1，I2，J与超言行材料的三个主拉伸比λ1，λ2，λ3的关系为：

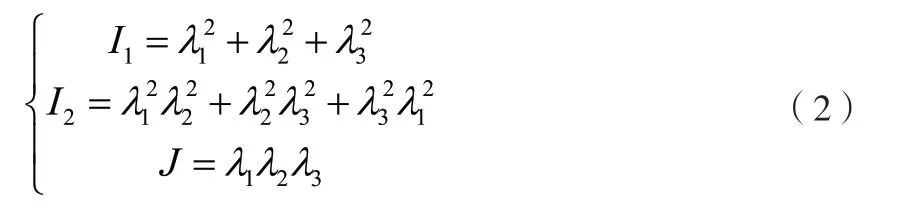
1.1 Mooney-Rivlin模型

Mooney-Rivlin模型的应变势能为[11]：

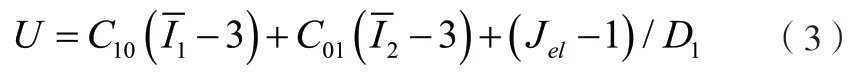
式中：

C10、C01、D1—材料模型参数；

Jel—弹性体积比；

和—第一、二阶应变不变量。

1.2 Ogden模型

Ogden模型的应变势能为[11]：

式中：

iµ和iα—均为描述温度函数的模型参数。

1.3 Van der Waals模型

Van der Waals模型的应变势能为[11]：

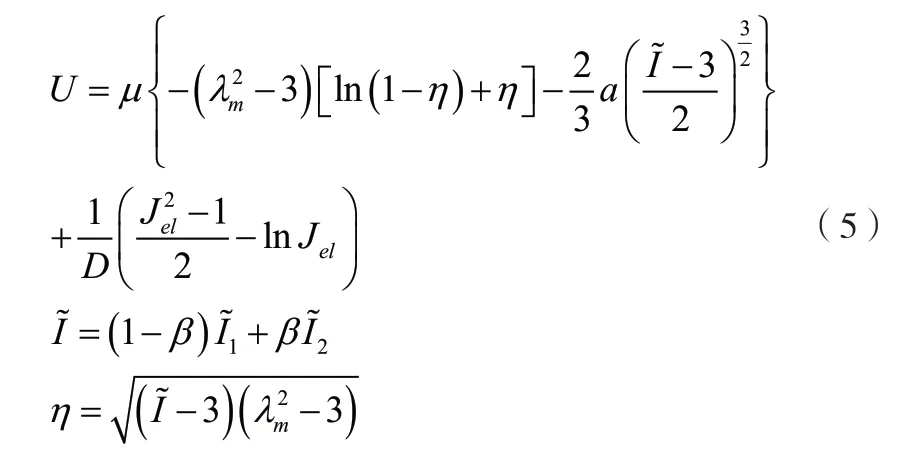
式中：

µ、mλ、a、β和D—模型参数。

1.4 Marlow模型

Marlow模型的应变势能为[11]：

式中：

Udev和Uvol—分别为偏量部分和体积部分。

2 超弹性材料模型的参数拟合

假设材料体积不可压缩，则单轴拉伸、等双轴拉伸和平面拉伸的应变势能和工程应力iσ的关系为[3]：

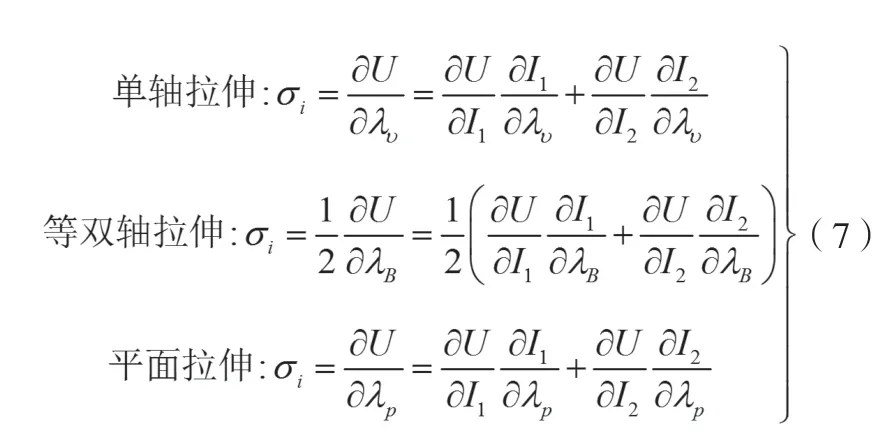
式中：

υ

λ、Bλ和pλ—分别为实验测得的单轴拉伸、等双轴拉伸和平面拉伸的拉伸比。

应变不变量为[3]：

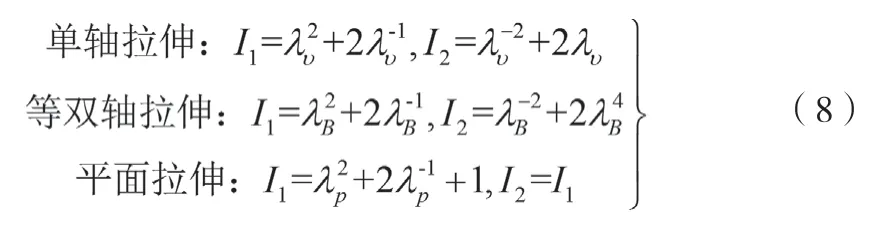
通过实验测得的橡胶试片的应力-应变曲线，可利用最小二乘法求得工程应力的相对误差[11]：

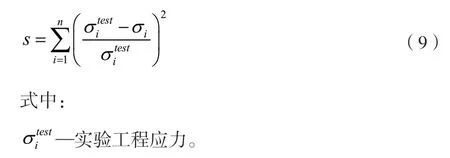
2.1橡胶材料模型参数的实验与拟合

根据上节所述的橡胶不同本构模型参数的获取方式，在对橡胶材料进行应力-应变测试时，一般需要对橡胶试件进行单轴拉伸、等双轴拉伸机平面剪切试验。鉴于实验设备的紧缺，本次仅对橡胶试件进行单轴拉伸试验。

选取横截面为4*1.9 mm，邵氏硬度为50、55、60的橡胶样件在拉伸试验机进行单轴拉伸试验（橡胶支座的设计硬度为55度，故上下浮动5度）。由于橡胶材料存在Mullins效应，取橡胶试件循环加载的最后一次应力-应变数据作为实测的工程应力-应变关系。

将不同本构模型的拟合曲线与测试所得应力-应变曲线相比，结果如图1所示。

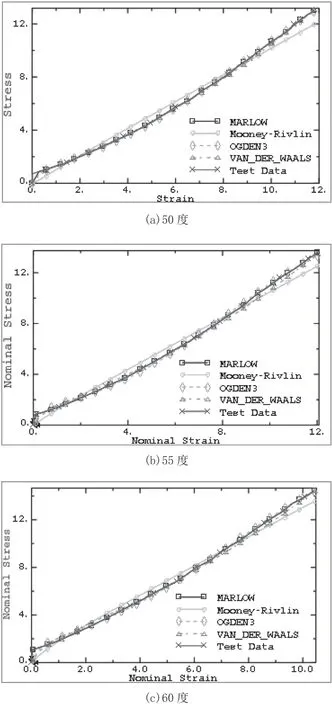
图1 不同硬度橡胶试件的工程应力-应变曲线

不同硬度的橡胶试件的不同本构模型参数及拟合的相对误差如表1~3所示。

表1 Mooney-Rivlin模型参数及误差

综合分析各图表可知，仅在橡胶材料试件单轴拉伸情况下拟合误差最小的为Ogden模型，平均误差为1.1 %左右；Van der Waals模型次之，平均误差为2.5 %左右；拟合最差的为Mooney-Rivlin模型，平均误差为5.4 %左右。由于Marlow模型为直接逼近，其拟合误差最小，基本与实测的工程应力-应变曲线重合。

表2 Ogden模型参数及误差

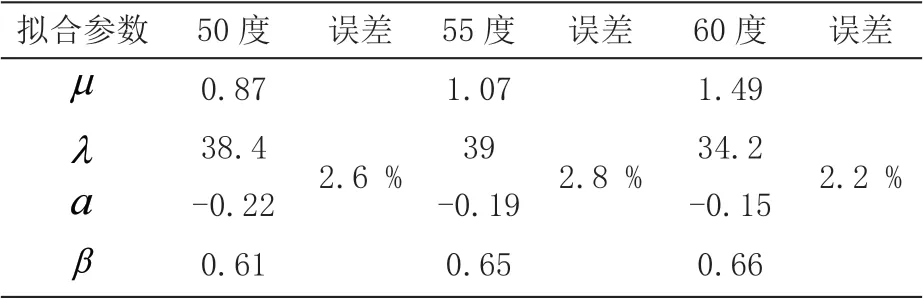
表3 Van der Waals模型参数及误差

3 前悬架橡胶支座力-位移关系的分析

对前悬架橡胶支座进行简化，建立其有限元模型，如图2所示，按支座静态测试状态施加边界条件。在模型中施加沿轴向的位移载荷，载荷大小为14 mm。分别将邵氏硬度为50、55、60度的橡胶材料试件拟合的本构模型参数带入有限元模型中，计算模型的力-位移关系。

图2 前悬架橡胶支座的有限元模型

前悬架橡胶支座的静态测试在拉力试验机上进行，通过对其循环加载，施加14 mm的位移载荷，速率为1 mm/s，提取反力来获取其力-位移曲线。

图3为不同橡胶硬度的前悬架橡胶支座的仿真与测试力-位移曲线。在0~14 mm的加载范围内，三个本构模型的仿真结果的趋势与测试结果基本一致。使用Ogden本构模型的参数进行仿真的结果最为接近测试曲线；Mooney-Rivlin模型在位移超过10 mm后，其力载荷低于测试结果。在数值上，三个模型的拟合结果与测试结果有一定偏差，其原因有多个方面：①橡胶的超弹性本构模型参数拟合仅有单轴拉伸数据，缺少等双轴拉伸和平面拉伸的数据；②在橡胶材料试件与前悬架橡胶支架的实验中存在测试误差；③对于仿真模型的简化处理使得仿真结果与测试结果存在偏差等。

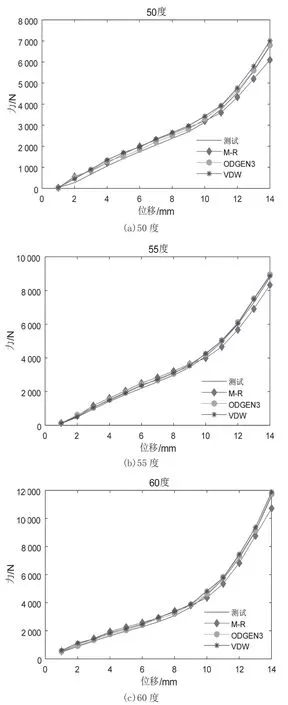
图3 不同橡胶硬度支座的力-位移曲线

4 结论

本文应用应变势能来表达橡胶超弹性材料的应力-应变关系，使用了不同本构模型来拟合橡胶的非线性，并进行了仿真与测试的对比，结论如下：

1）不同硬度的橡胶材料试件对超弹性本构模型参数的计算有较大影响。仅有材料单轴拉伸数据的情况下，在4种模型中，Ogden模型的应力-应变拟合误差较小，平均误差为1.1 %。

2）使用3种本构模型拟合的参数进行支座的力-位移仿真，总体的力-位移关系与测试结果基本一致，但数值上有一定偏差。