基于生成对抗网络的飞机燃油数据缺失值填充方法
郭毅博,牛猛,王海迪,陈艳华,薛均晓,袁玥,侯立硕,徐明亮,潘俊
(1.郑州大学信息工程学院,河南郑州450001;2.中国航空工业集团公司金城南京机电液压工程研究中心,江苏 南京211106)
0 引 言
燃油测量系统是飞机燃油系统的重要组成部分。对飞机各油箱内当前剩余燃油量的实时精确测算,是实现飞机耗油顺序优化、飞机重心控制及飞机热管理等的基础。飞机燃油测量精度对飞机续航时间、有效载重、重心等控制均有重要意义。
通过安装在飞机机身不同部位的各类传感器采集飞机燃油相关信息,例如,陀螺仪可采集飞行姿态,气压高度计可采集飞行高度,电容式测量杆可采集飞机油箱内燃油面的高度。传感器传输的数据随飞机状态的改变而变化,将传感器输出的数据组合起来便可得到一个多维时序数据,即飞机燃油数据。图1为飞机各个部位传感器数据采集示意,各时序数据反映了飞机的状态。常用的飞机燃油测量方法是通过分析飞机燃油数据,学习飞机运动姿态、飞机油箱内燃油面高度等信息与飞机燃油之间的映射关系得到的,其测量精度与燃油数据的质量息息相关。
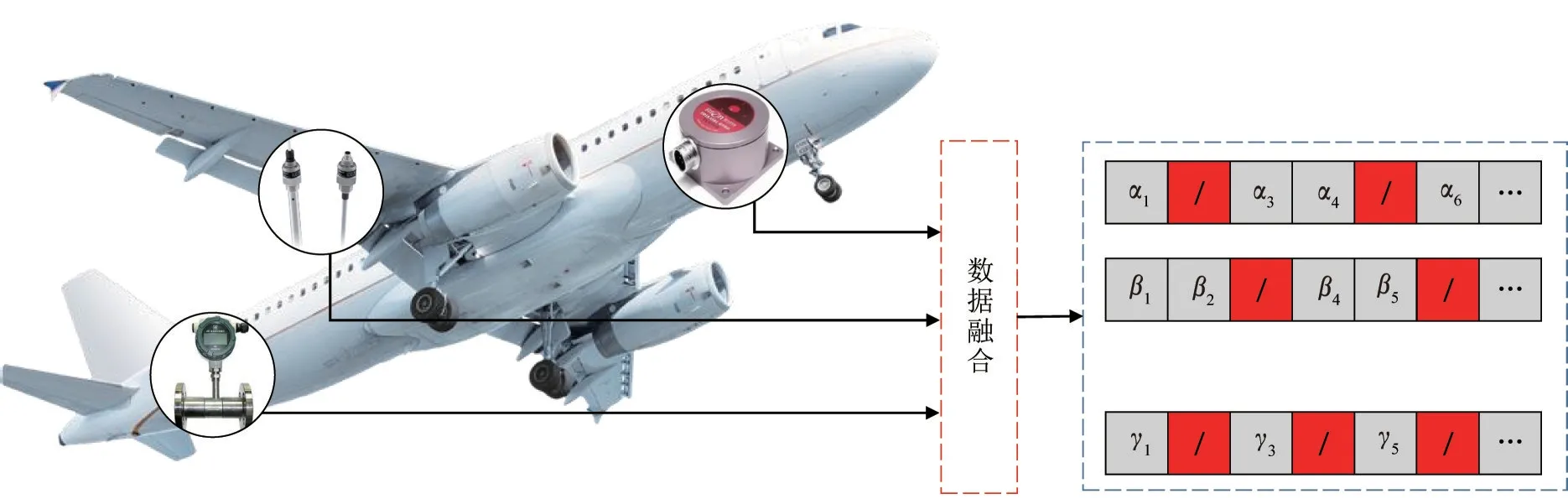
图1 飞机各个部位传感器数据采集示意Fig.1 Schematic diagram of sensor data acquisition in various parts of aircraft
然而,由于飞机高空飞行过程中受多种因素影响,燃油数据会出现相当规模的缺失或错误。例如,飞机在进行大幅度机动动作时,油箱内燃油会产生剧烈晃动,难以形成可测量的油面,测量杆难以采集准确数据。另外,传感器可能因受电磁干扰无法正常工作,或采集数据出现误差。同时,各类传感器的数据采集频率并不完全一致,在进行数据融合和时空对齐时易出现数据缺失,缺失数据常用“/”表示(如图1所示)。时序数据中部分信息缺失会导致其隐含的历史变化规律丢失,使得后续很难做出准确的分析和预测,因此,需对数据进行预处理。
对缺失值的处理方法主要有2种:直接删除法和缺失值填充法。直接删除法是直接丢弃包含缺失值样本的方法。该方法虽然可以保证数据完整,但因数据样本量减少,造成样本多样性缺失,不利于后续分析。缺失值填充法是根据特定规则填充缺失值的方法,主要分为基于统计学的填充方法、基于机器学习的填充方法和基于生成对抗网络的填充方法3种。其中,前2种填充方法没有考虑时间序列上下文关系,燃油数据缺失值填充效果较差;而基于生成对抗网络的填充方法引入了博弈论思想,使填充的完整序列数据更符合真实序列数据分布。然而,当输入数据过长时,基于生成对抗网络的填充方法会出现信息丢失,无法学习时序数据中较长时间段的历史变化规律,影响数据填充效果。
本文对基于生成对抗网络的缺失值填充方法进行了改进,在算法模型的生成器部分引入注意力机制的Seq2seq模型,这在一定程度上解决了输入数据过长时信息丢失的问题。此外,本文还将缺失数据位置信息用于填充算法,从而有效改善数据填充效果。
1 相关工作
1.1 基于统计学的缺失值填充方法
根据统计学规律进行缺失值填充。如AMIRI等[1]用 上 一 次 观 测 值(last)进 行 缺 失 值 填 充,PURWAR等[2]用众数(mode)进 行缺失值 填充,KANTARDZIC等[3]用均值(mean)进行缺失值填充,这些方法虽然能将缺失值补充完整,但因只考虑单个维度的统计信息,忽略了其他维度,导致填充效果较差。
1.2 基于机器学习的缺失值填充方法
通过机器学习相关算法构建填充模型、学习数据样本分布规律、生成相应的填充值。MAZUMDE等[4]采 用 基 于 期 望 最 大 化(expectationmaximization,EM)的填充方法,不断迭代计算最大化期望和求解期望至均衡,得到概率模型,并将由概率模型得到的估计值作为填充值。HASTIE等[5]采用基于矩阵分解(matrix factorization,MF)的填充方法,将缺失时序数据看作矩阵,先使用奇异值分解(SVD)[6]、主 成 分 分 析(PCA)[7]、非 负 矩 阵 分 解(NMF)[8]、概率矩阵分解(PMF)[9]等算法将矩阵分解为多个子矩阵的乘积,再将子矩阵相乘得到对应的相似矩阵,最后进行缺失值填充。NIKFALAZAR等[10]整合决策树与模糊聚类的优点,通过迭代学习对数值型缺失数据和分类型缺失数据进行插补。KHAN等[11]将单一和多种插补法混合,提出一种多链方程的单中心插补方法用于类别估算和数值数据的插补。冯宪凯等[12]对基于DBSCAN算法的缺失值填充方法进行了改进,通过定义由数据对象密集程度自适应调节大小的MinPts邻域,并用其代替不变的ε邻域,从而提高了处理后缺失值记录的正确率。BATISTA等[13]采用基于k近邻(k-nearest neighbor,k NN)的填充方法,先找到与时序数据中缺失值距离最近的k个数据,再将这些数据的均值作为填充值。参数k值的选择会影响该算法模型的精度,k值过小会导致模型精度下降。张楷卉等[14]用平均比率法进行基础填充,以提供完整数据条件,在模糊C均值聚类框架下进行同类数据聚集,并利用局部距离策略改进模糊C均值聚类,此方法主要用于处理大型数据集。以上方法在计算过程中均未考虑时序数据在时间维度上的上下文依赖关系,易造成填充值与时序数据的隐含规律不相符,填充效果较差,无法满足缺失值填充任务的要求。
基于此,考虑深度学习算法中循环神经网络在时间序列任务中的优秀表现,将循环神经网络应用于缺失值填充。CHE等[15]用基于循环神经网络的填充方法,先用部分完整的时序数据训练多层循环神经网络模型,再用该模型预测时序数据中每个缺失值。郝雨微[16]提出2种改进措施,一种是在深度模型中引入4种缺失模式用于预测任务,另一种是设计新的双向多任务循环结构,采用插补法进行缺失时序数据填充。FEDUS等[17]采用基于自编码器的填充方法,先用编码器将包含缺失值的时序数据映射为一个固定长度的中间向量,再将其解码为相应的完整时序数据,最后填充缺失值。
以上方法虽然能有效提取时序数据在时间维度上的上下文依赖关系,但需采用完整的数据集进行模型训练。另外,若用传统的填充算法对缺失时序数据先填充,再训练,则会导致模型精度降低。因此,基于机器学习的填充方法只适用于时序数据中缺失值占比较小且样本量较多的情况,即可从时序数据中挑选出足够的完整数据用于模型训练。
1.3 基于生成对抗网络的填充方法
通过生成对抗网络建立填充模型,学习数据集样本的分布规律,并将生成器输出作为填充值。YOON等[18]提出基于生成对抗网络的缺失值填充方法,使用生成器生成与原始数据集分布相同的新的数据样本,并根据生成样本进行缺失值填充。SHANG等[19]在此基础上对多模态数据进行了研究,该方法能够学习多模态数据各维度之间的关系,并以此填充某个模态数据中的缺失值。罗永洪等[20]根据生成对抗网络与时序数据时间间隔特性,对缺失的时序数据进行降维,以提高缺失值填充效率。以上3种方法均可直接对缺失数据进行训练,但均未考虑时序数据的上下文依赖关系,不适合时序数据。
LUO等[21]将自编码器模型引入生成对抗网络,通过运用循环神经网络取得了较好的填充效果。但当输入的时序数据较长时,由于编码器很难将所有重要信息压缩为一个低维中间向量,因此易出现信息丢失,这在一定程度上影响填充效果。为此,本文在生成器部分引入了注意力机制的Seq2seq模型,旨在有效解决信息丢失问题。
2 基于生成对抗网络的飞机燃油数据缺失值填充方法
2.1 问 题
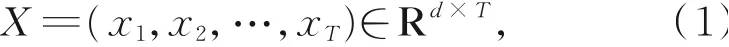
首先,定义缺失燃油数据为其中,x T可具体表示为x kt,表示该数据中时刻t数据的第k个元素值,d表示数据的维度,T表示数据的长度,R表示实数。
其次,定义缺失燃油数据相应的缺失标识矩阵Q∈Rd×T为
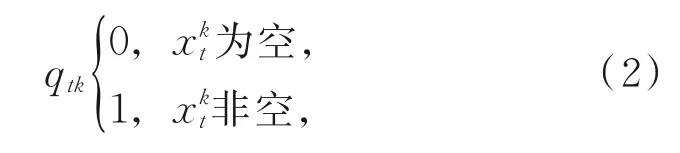
其中,qtk表示缺失标识矩阵第t行第k列的元素。
最后,填充完整的燃油数据可表示为

其中,x'T可具体表示为x k't,表示该数据时刻t数据的第k'个元素值。
真实完整的燃油数据可表示为

其中,y T可具体表示为y kt,表示该数据中时刻t数据的第k个元素值。
根据以上定义,举例说明如下。假设燃油数据为
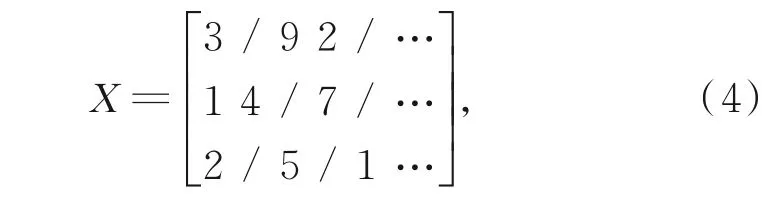
则对应的缺失标识矩阵为
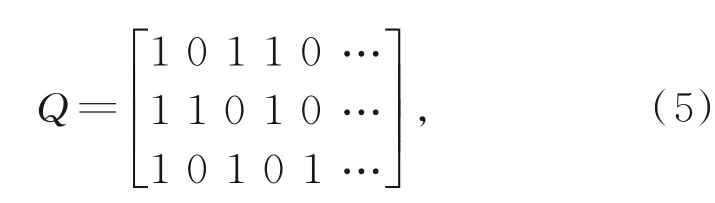
式(4)中,/表示缺失值,式(5)中,1表示数据完整,0表示数据缺失。
将缺失燃油数据填充完整,得到完整燃油数据,可表示为

2.2 方法框架
谷歌提出了可用于解决Seq2seq问题的Transformer模 型[22],该 模 型 以 全 注 意 力 层(attention)结构代替LSTM,实现了高效并行,但目前Transformer模型大多用于自然语言处理(natural language processing,NLP),较少用于时间序列,其在时序数据上的性能尚很难确定,而大量实验证明LSTM能够有效处理时序数据[23],将LSTM与生成对抗网络相结合可有效提高缺失值填充效果。将博弈论思想引入传统的生成对抗网络[21],所构建的模型主要包含生成器(G)和判别器(D)两部分。其中,生成器主要用于学习真实数据样本的分布状况,并生成完整燃油数据;判别器主要用于判断输入数据样本的真实性,即判断输入数据样本是真实的还是由生成器生成的。
为避免传统生成对抗网络训练困难、生成器生成数据缺乏多样性的问题,本文引入了Wasserstein生成对抗网络(WGAN)模型[25]的改进方法,即用W距离替代JS散度。WGAN的优化函数为
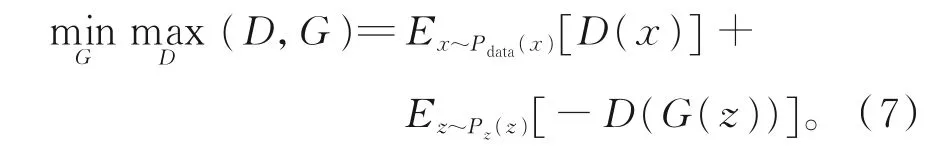
由于本文的目的是填充缺失值,而不是直接生成新的数据样本,因此需对生成器输入部分进行相应的改动。在传统的生成对抗网络中,生成器的输入是服从高斯分布的随机噪声向量,而在燃油数据缺失值填充中,其输入是一段包含缺失值的时间序列X。
本文方法的整体结构如图2所示。先通过编码器将生成器输入数据映射为一个维度固定的低维向量z,然后将向量z重构为完整的时序数据,得到完整时间序列Y'。此外,判别器的输入包含2种数据,一种为真的完整时间序列Y,另一种为假的填充后的完整时间序列Y';其输出为输入数据是真实样本的概率。生成器和判别器经交替迭代训练,最终达到均衡,此时二者的损失值不再降低,生成器的输出数据样本与真实完整序列数据样本的分布相符,之后只需将生成的数据填充至原始数据中的缺失处。
2.2.1 生成器结构
生成器内部采用Seq2seq模型[26],该模型通过自编码器实现,自编码器由一个编码器和一个解码器组成,其中编码器可将输入的缺失燃油数据压缩为多个低维中间向量z1,z2,…,zn,而解码器可通过解码这些中间向量得到完整的燃油数据。
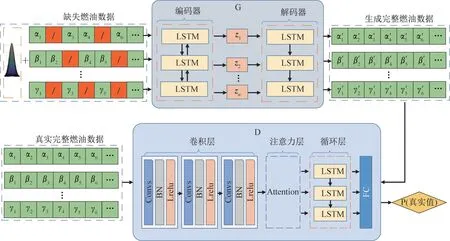
图2 本文方法整体结构Fig.2 The overall architecture of the method
本文通过向输入数据中加入噪声的方式增加数据多样性,增强Seq2seq模型的泛化能力。但直接以一定概率将输入数据置为0的方式会导致输入数据缺失率增加,不利于缺失值填充任务。为此,本文直接生成一个符合高斯分布的随机噪声向量,并将其与输入数据拼接为新的输入数据。此外,基于输入数据中缺失值的上下文依赖关系对缺失值填充任务的重要性,自编码器的2个部分均使用循环神经网络,其中,编码器使用BiLSTM模型[27],解码器使用LSTM模型[28]。
BiLSTM模型包含前向计算和后向计算两部分。在前向计算中,数据以正序输入,模型中时刻t的隐藏层状态h→t能学到时刻t之前的所有输入信息;在后向计算中,数据以逆序输入,模型中时刻t的隐藏层状态h←t能学到时刻t之后的所有输入信息。将2个隐藏层状态拼接起来,可得时刻t的隐藏层状态为[h→t,h←t]。在LSTM模型中,时刻t'的隐藏层状态为st'。
由于Seq2seq模型中引入了注意力机制[22],编码器与解码器之间保留了多个固定长度的中间向量zi。计算方法如下:
编码器中每个时刻的隐藏层状态ht与解码器中前一时刻的隐藏层状态st'-1之间的相关程度用et't表示
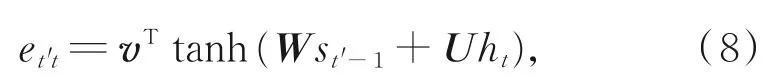
其中,v表示权重向量,W和U分别为权重矩阵。
对et't进行归一化,可得对应的注意力概率分布:
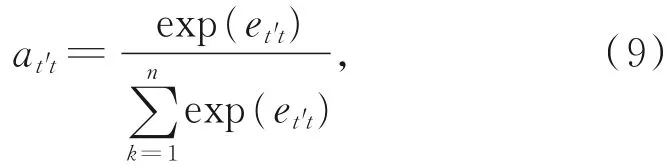
由ht和at't可得中间向量zt':
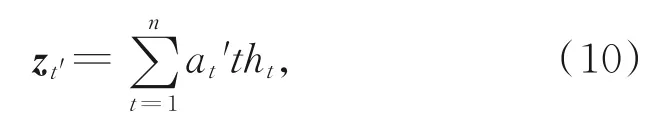
由zt'和st'-1可得解码器当前时刻的隐藏层状态:
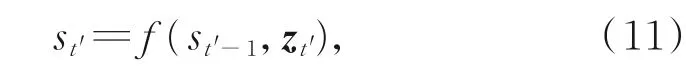
将所有时刻的解码器隐藏层状态信息用于填充数据。
为保证生成器输入数据与输出数据相关,在损失函数中引入了自编码器模型中的重建误差损失。生成器的损失函数包含对抗网络损失和重建误差两部分。其中,对抗网络损失用于评估生成器生成样本与真实样本的相似程度;重建误差用于评估时序数据缺失值填充效果。由于重建误差只针对非缺失部分的时序数据,需要先计算缺失标识矩阵。生成器的损失函数为
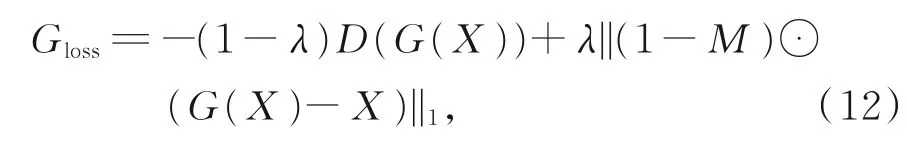
其中,λ表示降噪自编码器重构损失的系数;X表示输入的缺失部分的时序数据;M表示缺失标识矩阵。生成器的训练目标是使生成样本被识别为“真”的概率最大,并使重建误差最小。
2.2.2 判别器结构
判别器主要由卷积层、注意力层、循环层和连接层(FC)组成。卷积层主要用于学习时间维度上的短期上下文依赖关系;注意力层主要用于选择与输出相关性高的数据;循环层主要用于学习时间维度上的长期上下文依赖关系;连接层主要用于将循环层的输出映射为一维向量,用Softmax函数计算输入数据是“真”的概率。判别器的训练目标是尽可能地将真实样本识别为”真”,将生成样本识别为”假”。其注意力层结构如图3所示;损失函数为


图3 注意力层结构Fig.3 The architecture of deep attention
3 实验与分析
3.1 实验设置
实验数据来自某型号飞机油箱的多自由度地面转动试验台。该试验台能改变油箱的滚转角和俯仰角,使油箱能在一定角度范围内做旋转运动,模拟飞机的机动动作或模拟巡航飞行时油箱内燃油的变化情况。传感器的输出随时间变化,综合每时刻传感器的输出数据可得到一个多维时序数据,即飞机燃油数据,生成实验数据集。共进行了120组实验,每组实验时长为1 h,有效采样频率为5 Hz。
实验验证所用数据集有时间长度数据集和模型验证数据集2种。
3.1.1 时间长度数据集选择
首先,从燃油数据中筛选完整的子序列,根据不同的样本长度参数,将每个子序列分割为不同长度的数据样本,样本序列长度分别设为100,200,300,400,500,600,然后,随机丢弃30%的数据,根据丢弃位置生成相应的缺失标识矩阵,最后,将分割后的数据和相应的缺失标识矩阵汇总,得到不同样本序列长度的数据集。
3.1.2 参数λ选择
参数λ可影响对抗网络损失和重建损失在生成器损失函数中的比例,λ值越大,重建损失所占比例越大。用缺失比例为30%的模型验证数据集,模型中设置不同的参数λ值。
3.1.3 模型验证数据集选择
首先,从燃油数据中筛选出完整的子序列,将其分割为样本序列长度为100的数据样本,然后,随机丢弃不同比例的数据,丢弃比例分别设为10%,20%,30%,40%,50%,60%,根据丢弃位置生成相应的缺失标识矩阵,最后,将分割后的数据和相应的缺失标识矩阵汇总,得到不同缺失比例的数据集。缺失值填充任务数据集属性如表1所示。

表1 缺失值填充任务数据集属性Table 1 Missing value population task dataset attributes
3.2 评价指标
用均方误差(MSE)作为评价指标,评价填充效果。其计算公式为
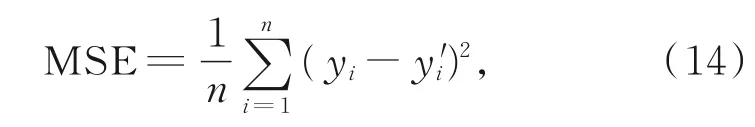
其中,n表示样本数,y i表示真实样本,y'i表示生成样本,MSE越小,说明y i与y'i之间差距越小,即准确度越高,填充效果越好。
3.3 实验结果及分析
3.3.1 不同样本序列长度对比实验
不同样本序列长度下填充方法的填充效果如图4(a)所示。随着样本序列长度的增加,填充方法的MSE逐渐提升,当样本序列长度大于400后,MSE基本趋于稳定。考虑样本序列长度对填充速度的影响,将样本序列长度设置为400。
3.3.2 参数λ选择实验
不同参数λ下的填充效果如图4(b)所示。当参数λ接近于1或0时,填充效果较差,即生成器损失函数的两部分均有助于提升填充效果。当参数λ为0.3时,MSE最低,即填充效果最佳。
3.3.3 不同缺失比例下填充算法对比实验
图4(c)为不同缺失比例下基于last、mean、MF、EM、k NN、GAIN及本文方法7种填充方法的填充效果对比。
由图4(c)可知,各填充方法的MSE随缺失比例的增加整体呈上升趋势,说明缺失比例是影响填充方法准确度的重要因素之一。此外,在缺失比例相同的情况下,本文方法的MSE均低于其他填充方法,说明7种方法中本文方法的填充效果最佳。

图4 实验结果对比Fig.4 Comparative experimental results
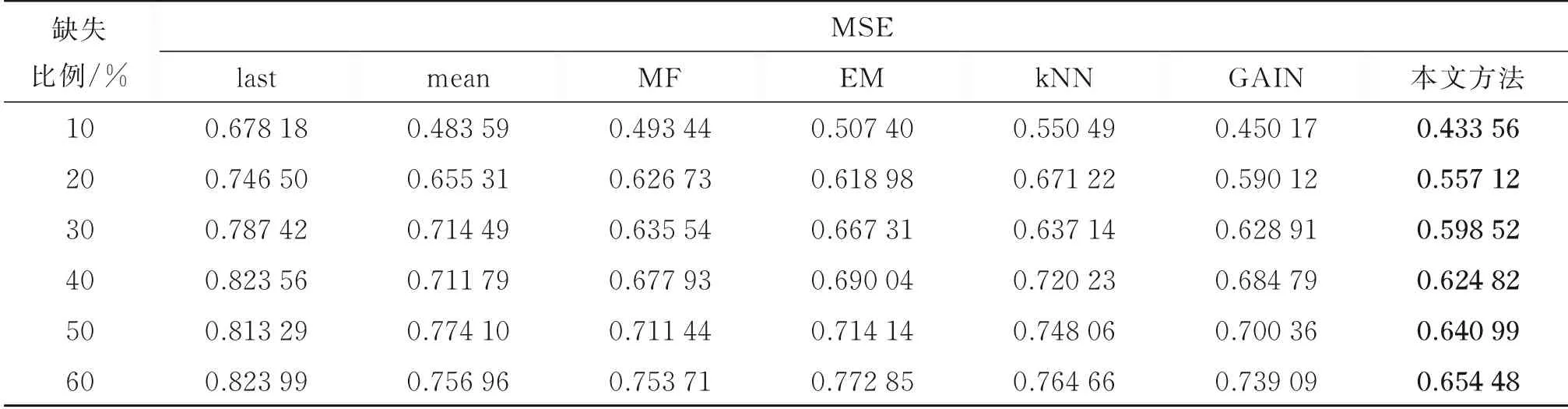
表2 不同缺失比例下各填充方法的均方误差Table 2 MSE of various filling algorithms at different missing scales
各填充方法在不同缺失比例下的MSE如表2所示,整体来看,本文方法在各缺失比例下均能达到最佳填充效果。
4 结 论
提出了一种基于生成对抗网络的飞机燃油数据缺失值填充方法,并针对地面转动试验台采集到的飞机燃油数据进行缺失值填充实验。为解决输入数据较长时存在的信息缺失问题,在生成器部分引入了注意力机制的Seq2seq模型。此外,用缺失标识矩阵优化损失函数。结果表明,与其他6种填充方法相比,本文方法填充效果更佳,学习能力更强,可应用于其他领域的时序数据缺失值填充及辅助后续数据分析,对提升飞机燃油测量等的精度有重要意义。

