黏性土剪切蠕变特性研究进展*

陈茂 张家明 龙郧铠

(昆明理工大学建筑工程学院 昆明 650500)

0 引言

滑坡灾害的启动往往经历了长期、缓慢的蠕变过程，土体结构从初始变形到完全破坏的过程中伴随着一套复杂的蠕变本构关系。诱发滑坡灾害的因素主要分为内、外两个方面，一方面是滑带土的矿物成分、颗粒级配以及微观结构等内部因素，另一方面则是自然侵蚀、降雨和地下水、库水位变化以及人类活动等[1-5]外界成因，而外界因素也主要是土体内部应力环境的改变[6]。降雨、地下水及水位变化等外界环境不断改变滑带的应力场和渗流场状态，从而影响坡体的整体稳定性。比如，三峡库区侏罗系顺层滑坡主要是由于特殊的动水效应引起的蠕变失稳[7]；白家包滑坡则是由于库区水位迅速下降改变了土体应力场状态，降低了坡体整体稳定性，在同周期降雨条件下加快了坡体变形，最终发生蠕变破坏[8]。

土体蠕变是滑坡演变的早期状态[9]，其与应力环境密切相关。三峡库区马家沟滑坡由于库水位变化导致坡体渗流场状态发生改变，影响了滑带土的应力场分布特征，从而诱发坡体发生蠕动型滑坡失稳[10]；位于湖北省巴东县信陵镇的临江坡体，由于移民搬入以及避险搬出等特殊人类活动改变了土体内部的应力路径，从而影响了渐进性滑坡的变形和稳定[11]。

随着全球基础投资建设规模的不断扩大，剪切蠕变诱发的自然或工程滑坡灾害也越发频繁，已经造成了大量的经济损失和人员伤亡，所以针对既有研究成果，开展黏性土剪切蠕变的研究具有科学的理论意义和实际的工程效益。本文主要从黏性土的剪切蠕变性质(试验方法、蠕变阶段及变形特征)、力学强度特征(分类、影响因素、演变关系)以及蠕变本构模型(理论成果、元件模型、经验模型)等几个角度进行综述，并对其中一些方面进行探讨分析。最后针对当前存在的问题提出了建议与展望，以期能为黏性土剪切蠕变的研究提供科学理论依据。

1 剪切蠕变试验研究方法

根据既有学者研究成果，由于复杂的室外条件，黏性土剪切蠕变特性的研究方法常采用室内环剪试验[12]、三轴压缩试验[7,13-14]以及直剪蠕变试验[15-16]。通过整理分析文献资料[12-18]，对黏性土剪切蠕变试验方法做出总结(见表1)。

表1 黏性土剪切蠕变试验方法

2 黏性土蠕变阶段及变形特征

针对黏性土蠕变阶段及变形特征，已有许多学者做了相关讨论。研究表明：黏性土在蠕变过程中呈现阶段性变化特点，且伴随着衰减变形与非衰减变形特征。龙建辉等[18]以应力状态和含水率为控制变量，采用三轴蠕变试验和直剪蠕变试验研究了黄土坡黏性土蠕变阶段特征，结果表明：研究区黏性土蠕变过程经历了3个阶段，即等速阶段、加速阶段以及蠕变破坏阶段；周静静等[19]采用直剪蠕变试验分析黏性土蠕变性质时，认为试样在每一级荷载作用下都经历了衰减阶段、稳态阶段，最后在破坏偏应力作用下进入加速蠕变阶段；田文[20]采集了该研究区含粗颗粒的黏性土进行三轴蠕变试验，将黏性土蠕变过程划分为瞬时蠕变阶段、衰减蠕变阶段和稳态蠕变阶段3 个部分。

根据既有研究成果，黏性土蠕变过程呈现着复杂的阶段性变形特征。总体说来，黏性土从变形开始到最终破坏的过程可依次划分为瞬时变形阶段、衰减蠕变阶段、稳态蠕变阶段以及加速蠕变破坏阶段等4个部分，且在这一过程中伴随着衰减蠕变和非衰减蠕变的变形特征(见图1)。

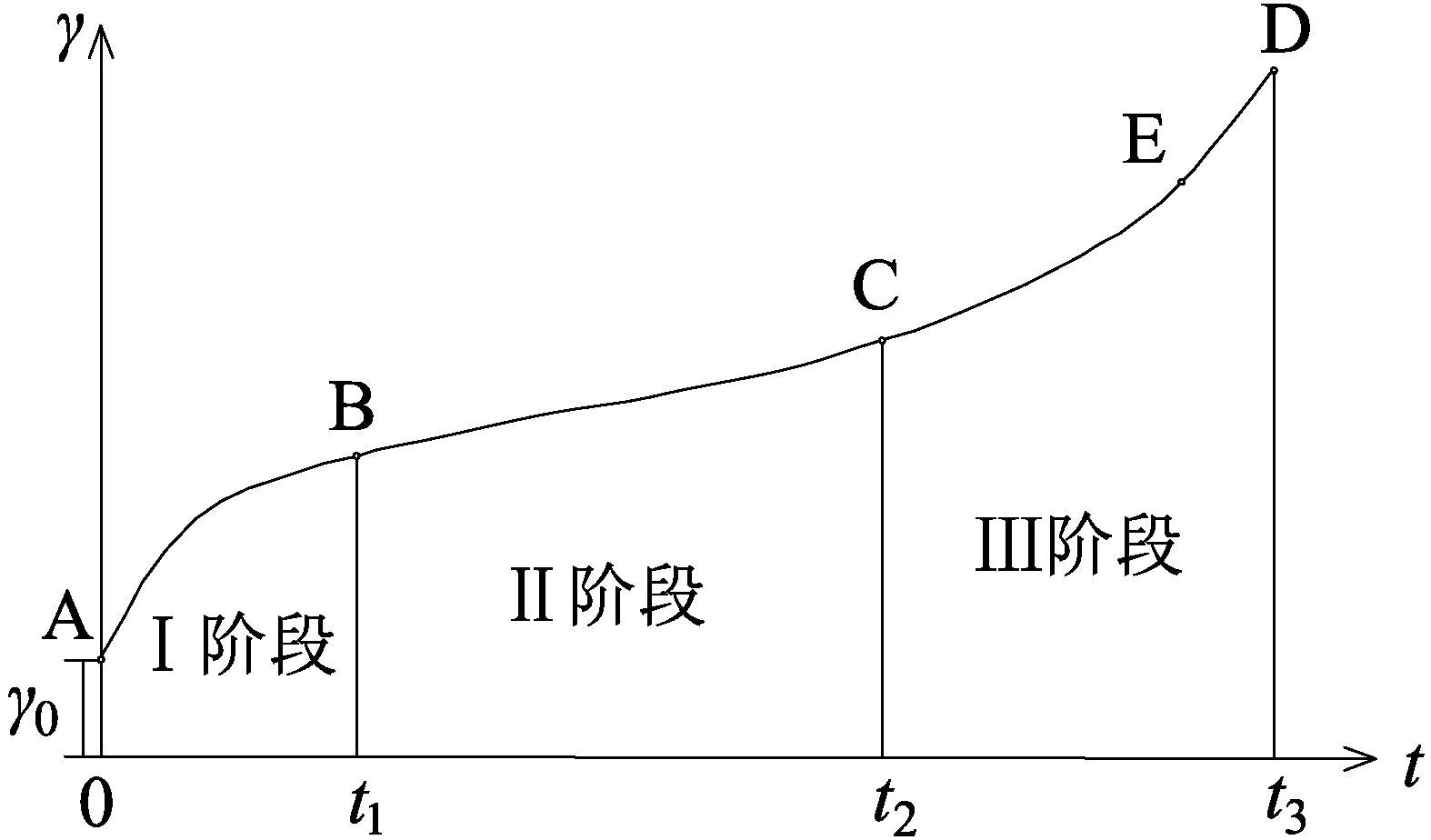
图1 变形随时间变化曲线

在荷载作用瞬间，土体中的部分水分子被排挤溢出，产生大量孔隙结构，这为土体颗粒位置变化腾出了场地空间。所以，荷载作用下的土颗粒三维空间位置不断发生调整，孔隙被不断填充，导致土体结构变形瞬间增大[14]，见图中0A段。在土体自重和外界环境的叠加效应下，土颗粒空间位置继续发生调整相互揉搓以适应土体骨架内的新应力链环境，最终趋于一个相对平衡稳定状态，即蠕变速率不断衰减[10,14]，见图中AB段。在经历瞬时蠕变和衰减蠕变阶段之后，土体结构内部应力环境处于基本稳定状态，黏性土蠕变速率趋于一个接近于零的常数，土体变形缓慢，历时周期漫长[7,10,13-14]，见图中BC段。经历长期的低速稳态变形后，土体内部应力等级累积达到破坏程度时，黏性土就会进入加速蠕变破坏阶段，土体内部结构规律发生紊乱，宏观上产生明显的破坏变形，呈似流体状态[17,21-22]，见图中CD段。而CD段严格上可细分为两个部分，一是发展着塑性变形但还未诱发破坏的CE段，二是微裂隙剧烈发展导致破坏变形的ED段[23]。

在黏性土剪切蠕变过程中，不同的变形阶段表现出不同的蠕变速率。即在黏性土蠕变过程中伴随衰减蠕变(AB段)和非衰减蠕变变形特征(BC段和CD段)。

3 黏性土力学强度特征

3.1 抗剪强度指标

黏性土抗剪强度指标控制着滑坡蠕变机理，其力学强度特征与斜坡整体形态和活动状态密切相关[24]。影响斜坡稳定性的强度指标主要包括：峰值强度、残余强度、启动强度、完全软化强度以及长期强度等5个方面[25]。

3.2 抗剪强度指标影响因素

黏性土在经历长期复杂应力作用后，土体的蠕动变形与力学强度特征具有时间效应关系[10,26]。影响黏性土力学强度特征的因素可以概括为：水化作用(水的弱化作用、含水率及水的化学成分)、土体先期变形量和时间效应、土体的矿物成分和粘粒含量、土体结构的内部连结特征、土体的粒度分布特征以及塑性指数等[27]。于是，针对黏性土5种力学强度特征值影响因素及关系进行分别讨论：

对于黏性土峰值强度的研究，龙建辉[28]认为其本质就是研究c值的特征规律。而c值的影响因素主要有有效法向应力、粘粒含量、粘土矿物和应力状态、密实度、剪切移动速率以及含水率等。研究表明：峰值强度与超固结比、有效法向应力、剪切速率、密实度等呈正相关性，而与含水率、粘粒含量呈负相关性。遇水后发生涨缩现象的亲水性粘土矿物可弱化黏性土峰值强度。不同应力状态下的土体强度指标也存在差异，一般认为轴对称应力状态和三向应力状态的峰值强度大于平面应力状态[26]。

经历大变形之后的黏性土，其内部结构出现重新组合的现象，土体颗粒间的摩擦力和咬合力通过不断调整抵抗外界应力场变化，最终趋于一个较稳定的状态，此时所达到的最小稳定状态的强度即为残余强度。而残余强度的影响因素主要为：土的矿物结构成分、颗粒体积大小、粘粒含量、塑性指数Ip、有效法向应力等[26-27]。研究表明：残余强度与粘粒含量、塑性指数呈负相关性，而与有效法向应力呈正线性关系。呈扁平或类扁平状粘土矿物的残余强度小于次角状或针状颗粒的粘土矿物。

在滑坡发育过程中，由于复杂多变的应力状态，黏性土启动强度常是一个不易确定的指标，其量值可能等于峰值强度、残余强度、软化强度以及长期抗剪强度，但也有可能介于上述强度指标之间[25]。龙建辉[28]引入“启动含水率”这一特征含水率来反算确定了土体的启动强度。结果表明：启动含水率接近于塑性含水率，可认为塑性含水率对应的强度即为启动强度。

SKEMPTON A W[29]认为经历峰值阶段后的强度下降原因可归结于两点：首先是土体含水量的增加，其次是由于粘土颗粒与剪切方向平行的重定向。对于软化强度的研究，有关学者[26]认为由于含水率与土体中吸附粘聚力和加固粘聚力的关系，导致土体结构间的联结力发生弱化。所以，土体在饱和状态下的软化强度与φ值密切相关，其影响因素主要有：粘粒粒级、粘粒形状、液塑限指标、饱和含水率、粘粒粒径级配分布以及有效正应力等。研究表明：黏性土完全软化摩擦角随粘粒粒级、液限的增大不断减小，而含水率与其相关性不大。摩擦角的变化也受粘性形状的影响，即粘粒的片状化发育使得φ值不断减小。

黏性土长期强度往往控制着滑坡的变形，其影响因素主要受土体含水量、密度、粒度成分、矿物成分、化学组分、试验条件等控制。研究表明：长期强度值随土体含水量增加而减小，但与密度呈正相关性。黏性土粒度成分影响着c、φ值，土体中细颗粒含量越多，c值越大，而φ值越小。亲水性矿物由于特殊的吸水胀缩性，会导致土体强度不断弱化[30]。

3.3 力学强度指标演变关系特征

黏性土从变形开始到加速破坏的过程中，各强度特征之间密切相关。龙建辉[28]针对泾阳南塬黏性土的峰值抗剪强度、完全软化强度以及残余强度之间的演变关系做了研究(见图2)。对于非饱和土而言，经历峰值强度后的强度指标在不断降低，可化分为两个阶段：第一阶段是土体内部含水率增加弱化了结构间的粘聚力，导致结构体强度逐渐丧失，最后达到软化点进入完全软化阶段；第二阶段是由于土体中部分颗粒与剪切方向平行排列所导致，土颗粒经过漫长的调整后强度不断降低，最终达到残余强度状态。黏性土在蠕变过程中，其力学强度指标在不断降低，经历长期动水作用和剪切破坏，土体结构稳定性逐渐减弱。

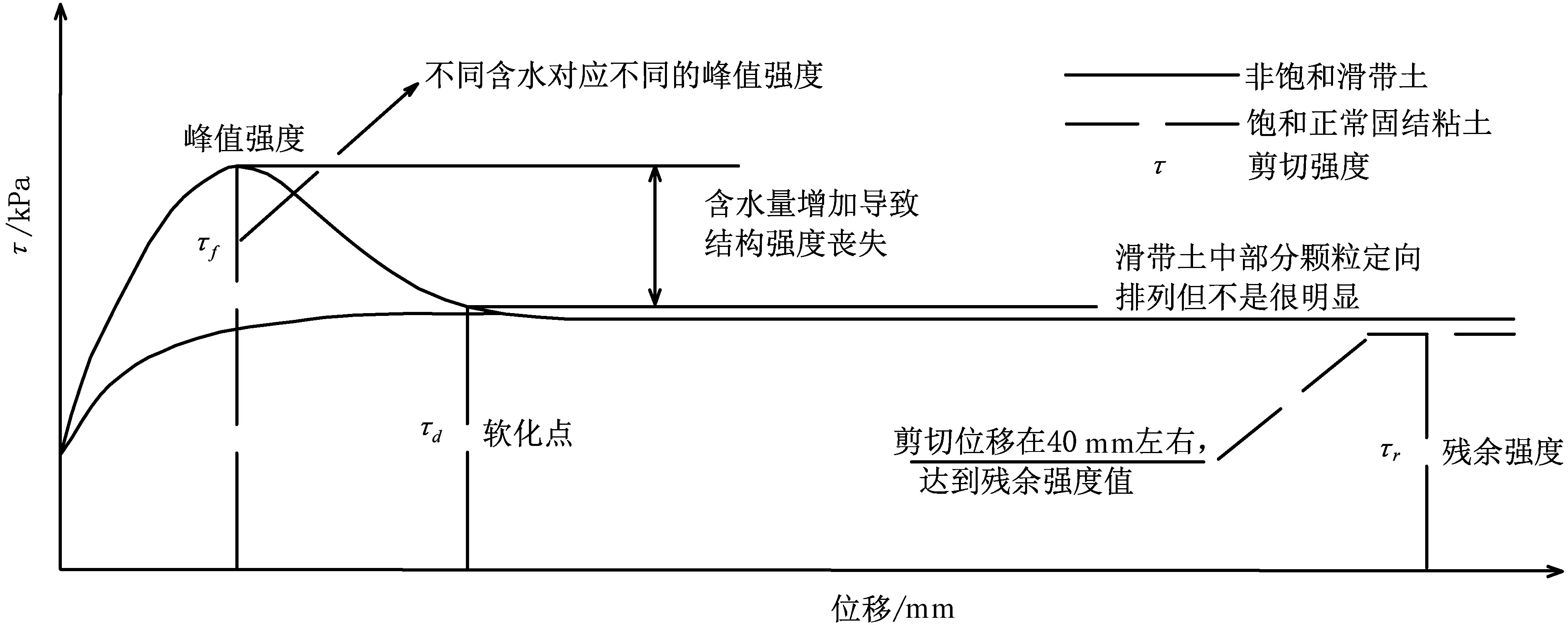
图2 黄土滑坡滑带土强度特征参数相互关系示意

4 黏性土蠕变本构模型

4.1 蠕变本构模型理论成果

土体的蠕变模型宏观上分为3类[31]，即经验-半经验模型、基于一般流变理论的元件模型以及黏弹塑性模型。经验-半经验模型常采用半对数或双对数坐标系来表达应力-应变-时间关系[32-33]。一般流变理论模型主要通过元件模型(Maxwell模型、Kelvin模型以及Burgers模型)建立数学方程表达式来表征土体蠕变特征[31,34-35]。黏弹塑性模型源于经典塑性理论，普遍认为蠕动势和塑性势具有一致性。本章基于蠕变本构模型研究成果，开展对经验模型与元件模型的讨论。

4.2 经验模型

对于经验模型的研究，国内外相关学者已开展了大量的研究，针对不同的变形特征建立对应的蠕变模型能更好的模拟和监测滑坡的位移动态。陈晶晶等[36]针对清江古树滑带土引入Mesri模型和Singh-Mitchell模型描述了土体的蠕变特性，研究表明该模型由于参数少、适应性强能很好的表达土体的应力-应变关系；王琛等[37]以三峡库区古滑坡为研究对象，建立了描述黏性土变形的Singh-Mitchell经典蠕变方程，即变形函数关系采用指数函数描述，时间函数关系采用幂函数描述。

根据文献[23]及经验模型研究成果，描述土体应变-时间关系(时间函数)常采用幂函数、指数函数、对数函数或者双曲线函数，而描述应力-应变关系(变形函数)宜采用幂函数或双曲线函数。典型的经验模型有Singh-Mitchell模型和Mesri模型，两者的变形函数分别采用指数函数和双曲线函数，而时间函数则都采用幂函数[38]。

4.2.1 Singh-Mitchell经典蠕变模型

SINGH A等[39]在单级常应力加载和排水不排水三轴压缩试验的基础上，提出了可描述20%～80%剪应力水平范围的应力-应变-时间经验关系。认为可采用指数函数描述土体应力-应变关系，应变-时间关系采用幂函数能很好的描述土体的蠕变特性，写成应变率-应力水平-时间关系，可表示为

ε=AreαDr(t1/t)m

(1)

式中，ε为任一时刻t的轴向应变速率；t为受荷时间；Dr=(σ1-σ3)/(σ1-σ3)f，为剪应力水平，(σ1-σ3)f可由常规三轴排水压缩试验获取；Ar为单位参考时间t1， (σ1-σ3)=0时的应变速率；m为lnε-lnt关系图中直线的斜率；α为应变速率对数与剪应力关系图中线性段的斜率。式(1)即经典的Singh-Mitchell蠕变模型，只需确定Ar，α和m这3个参数。

在m≠1且初始应变ε0=0时，式(1)积分可推导为

ε=BeβDr(t/t1)m

(2)

式中，B=Art1/(1-m)，β=α，λ=1-m。故Singh-Mitchell蠕变模型需要确定的是B、β及λ这3个参数。

4.2.2 Mesri经典蠕变模型

Mesri经典蠕变模型中应力-应变关系采用双曲线函数描述，而应变-时间关系则采用幂函数来描述，其蠕变方程可表示为

(3)

式中，ε为轴向应变；t为蠕变时间；Eu切线模量；Su为抗剪强度；Rf为破坏应力比；Dr=(σ1-σ3)/(σ1-σ3)f，定义为剪应力水平；t1为参考时间；λ为试验常数。

当t=t1时，式(3)可表示为

(4)

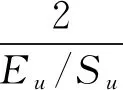
4.3 元件模型

黏性土在蠕变过程中呈现多阶段的变形特征，不同阶段土体表现出不同的蠕变规律。故在不同阶段选用合理的蠕变模型能更准确的模拟黏性土的变形特性。于是，在瞬时变形阶段黏性土产生弹性变形，此土体的蠕变特征可以用弹性元件来模拟。随着应力等级和时间效应的累积，黏性土的变形逐渐步入衰减阶段，蠕变速率不断减小。该阶段的蠕变特性适用于Kelvin体来模拟。将上述弹性元件和Kelvin体串联起来即可描述瞬时和衰减阶段的蠕变特征。随着应力条件不断改变，剪应力大于长期强度，土体蠕变进入长期稳态阶段，最后达到加速失稳破坏阶段。于是，在弹性元件和Kelvin体的基础上再串联一个黏性元件即可描述稳态变形阶段的蠕变特征。将弹性元件和黏性元件串联起来就可以建立描述瞬时变形和匀速变形阶段的Maxwell体[40]。

根据既有元件模型研究成果，本节主要讨论典型元件模型(Maxwell体、Kelvin体及Burgers模型)在蠕变变形中的应用。元件模型是由基本元件在不同组合情况下形成的，用以模拟土体的蠕变效应。常见的基本元件有弹簧、黏壶和滑片，分别用于描述土体的弹性、黏性及塑性变形。由弹簧和黏壶并联形成的元件模型，即Kelvin体，见图3(a)，主要用于模拟土衰减阶段的蠕变特征[6,24]；而由两者串联则形成Maxwell体，见图3(b)，主要描述土体瞬时和匀速变形阶段的蠕变特性。Burgers模型是由Maxwell体和Kelvin体串联形成(图4)，其可以反映土蠕变过程中的减速和稳定变形特征[41]。

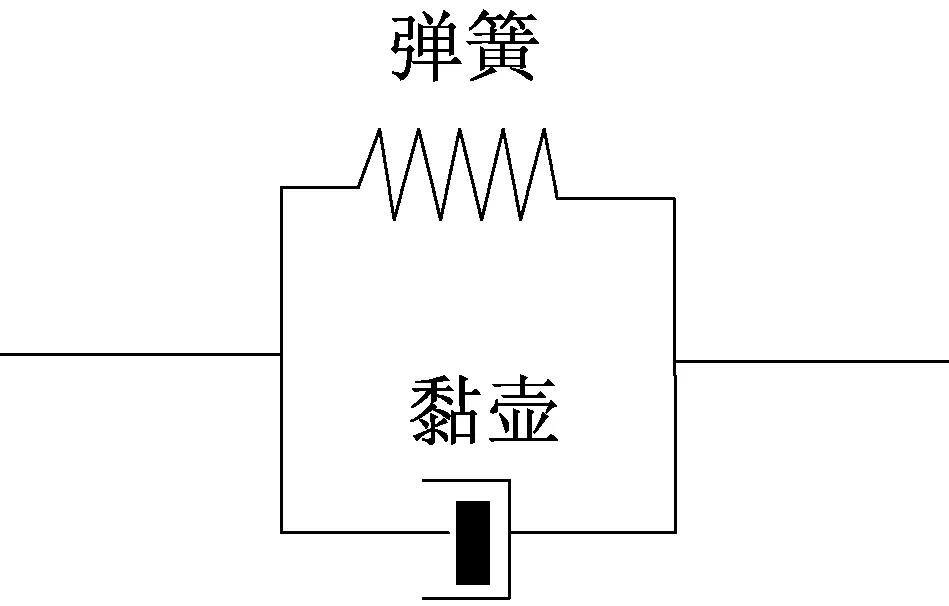
(a) Kelvin

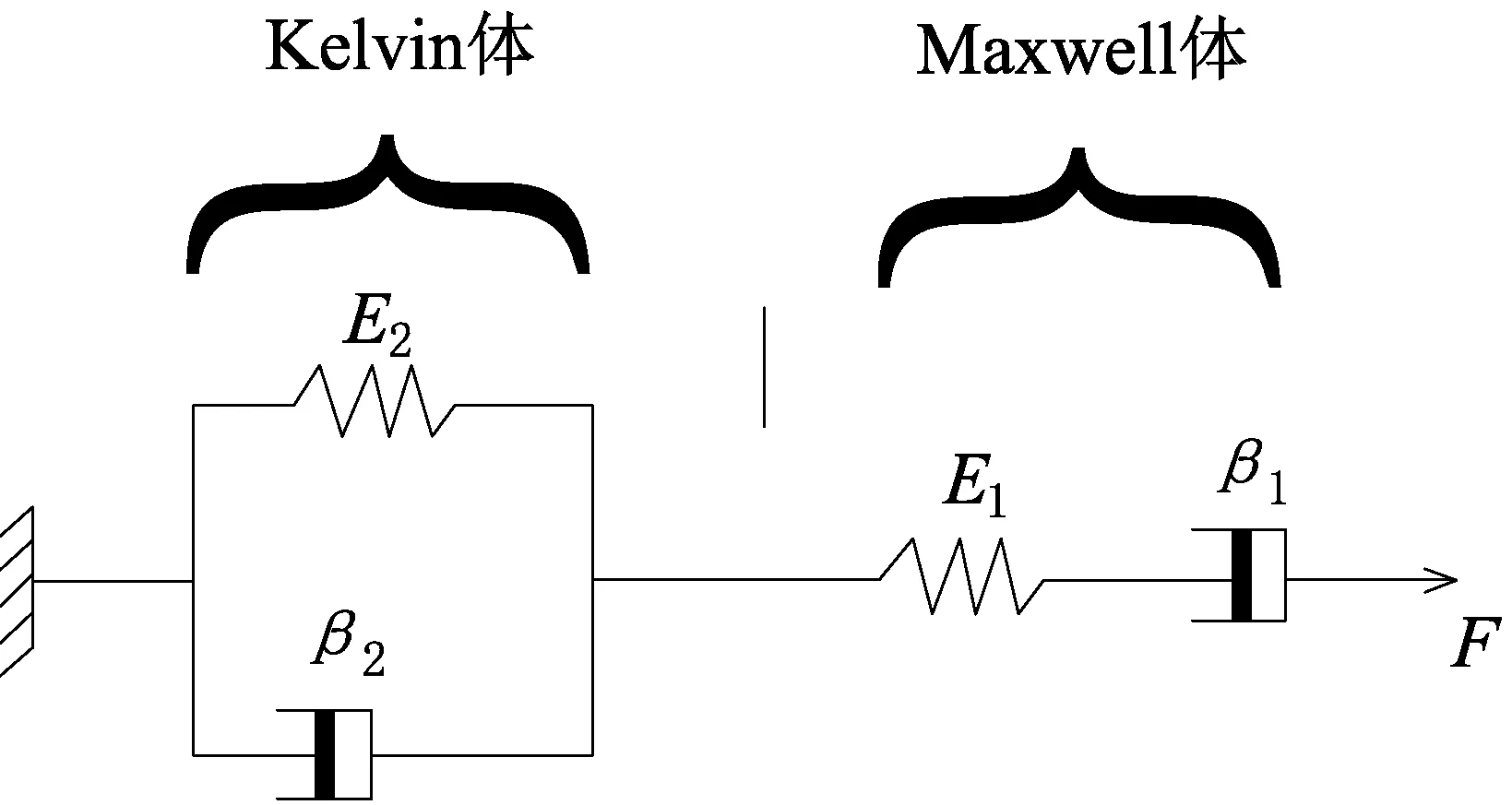
图4 Burgers 模型

4.4 元件模型与经验模型对比

根据已有研究成果，将黏性土蠕变本构模型划分为经验模型和元件模型进行对比分析(见表2)。

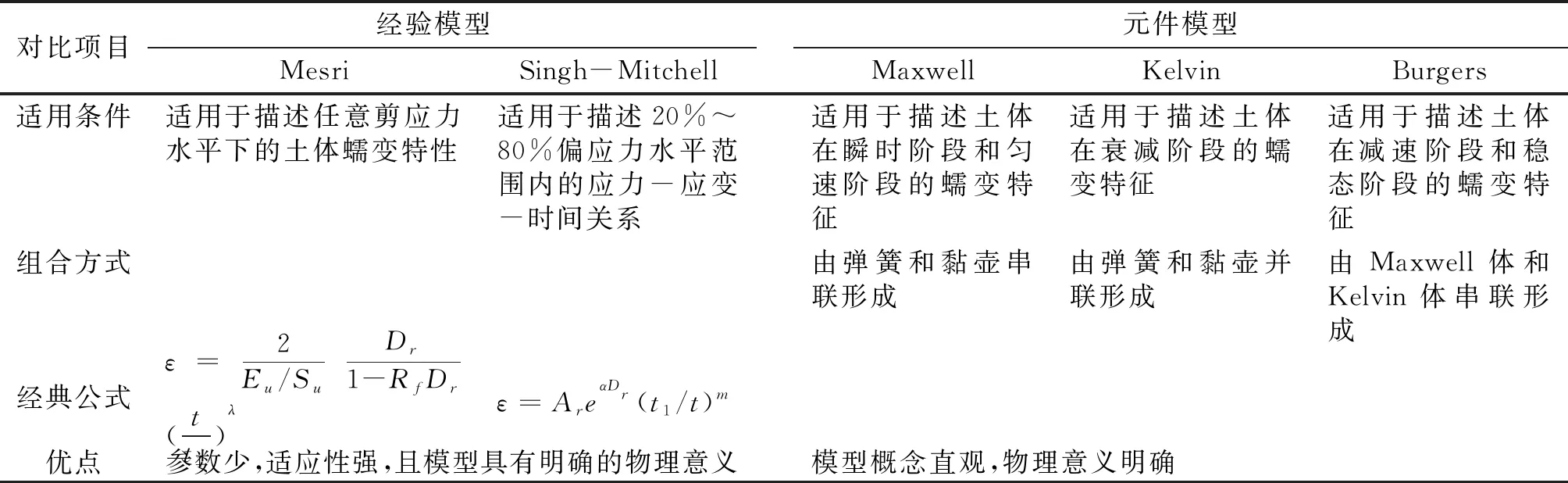
表2 黏性土蠕变本构模型对比

续表2

5 展望与建议

(1)蠕变本构模型可以很好的描述黏性土体在整个蠕变阶段的变形特征。从微观和宏观角度出发，建立全面的蠕变本构模型体系能更好的表征土体蠕变过程。研究表明：目前国内外学者对于蠕变模型的建立多集中在宏观模型，从细微观角度建立微观模型的研究理论成果较少，但微观结构常控制着土体的宏观变形。所以，今后的研究应多集中于微观模型的建立，完善蠕变模型系统以更加全面地分析土体变形特征。

(2)黏性土从初始变形到加速破坏伴随着多阶段的蠕变特性，根据不同阶段的变形特征建立对应的蠕变模型能更准确地反映土体的变形过程。研究表明：当土体进入加速蠕变阶段时，其内部结构应力场环境复杂多变，导致该阶段元件模型的建立仍是一个较大的技术空白。于是，基于既有成果，加快蠕变阶段模型的建立是未来的研究方向。

(3)新技术和研究方法的应用是今后促进剪切蠕变发展的一项重要手段。改进现有试验设备仪器在实际应用中的不足以及完善试验操作过程中的技术方法，同时引进一些比较前沿的技术手段：比如应用于微观结构方面的CT技术、数字图像测量以及红外光谱分析技术等，而应用于模型建立方面的物理、数学以及计算机技术等都是今后剪切蠕变研究发展方向。

6 结论

(1)黏性土的变形破坏是一个长期缓慢的过程，土体呈现出复杂的蠕变阶段和变形特征，即土体从初始变形到破坏的过程经历了瞬时变形、衰减蠕变、稳态蠕变以及加速蠕变破坏等4个阶段，并伴有衰减蠕变和非衰减蠕变变形特征。

(2)由于室外复杂的环境条件，黏性土剪切蠕变特性研究方法常采用室内环剪试验、三轴压缩试验以及直剪蠕变试验。

(3)黏性土整体稳定性和活动状态与土体抗剪强度指标(峰值强度、残余强度、滑坡启动强度、完全软化强度以及长期强度等5个方面)密切相关。影响黏性土力学强度特性的因素有：水化作用(水的弱化作用、含水率及水的化学成分)、滑土体先期变形量和时间效应、滑土体的矿物成分和粘粒含量、滑体结构的内部连结特征、滑土体的粒度分布特征以及塑性指数等。

(4)建立合理的蠕变模型能更好的反映土在变形过程中的蠕变特征。既有研究表明：Maxwell体能较好的反映土体在瞬时和匀速阶段变形特征，Kelvin体可以模拟滑土体在衰减过程中的蠕变特性，由Maxwell体和Kelvin体串联形成的Buergers模型可以反映滑土体在蠕变过程中的衰减和稳态变形特性。

(5)基于剪切蠕变性质的研究成果，今后的研究方向集中于以下几个方面：微观模型的研究；新技术和研究方法的应用和改进；建立可描述加速蠕变阶段的元件模型。