地铁车站二维抗震分析的中柱简化方式对比
李 伟 昝子卉 赵 密
(1.北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124; 2.广州地铁设计研究院股份有限公司,广东 广州 510000)
1 概述
1995年日本阪神地震,大开地铁车站的严重破坏[1]引起人们对于地下结构抗震的关注和重视。近年来,科研人员围绕地下结构抗震开展了大量研究工作[2-4]。为了简化计算,提高效率,地铁车站横断面抗震分析通常采用考虑土—结构相互作用的二维平面应变模型,中柱简化为沿纵向连续墙体。为了降低中柱简化处理的误差,通过折减等效墙体的几何尺寸或材料参数使其具有与中柱相同的截面抗弯刚度EI或抗压刚度EA。
目前,地铁车站的中柱等效方法有EI横向几何折减法[5](减小墙体横向宽度来保证中柱截面EI不变)、EA横向几何折减法[6](减小墙体横向宽度来保证中柱截面横向EA不变)、纵向几何折减法(将中柱平面应变单元厚度取为中柱纵向宽度,除中柱以外的土和结构平面应变单元厚度取为纵向一跨尺寸)和弹模折减法[7-9](减小墙体材料弹性模量E来保证中柱截面EA和EI不变)。李猛[10]利用EI横向几何折减法对地铁车站中柱进行简化,研究发现,地铁车站最薄弱的位置是侧墙和中柱,地震时易发生破坏。李延等[11]通过EI横向几何折减法将地铁车站中柱尺寸进行折减,发现平面模型与三维实际模型最危险的位置不一致,建议如果条件允许,还是应当采用三维实际模型。周小华[12]用等代框架法对地铁车站进行静力计算,所得结果与实际模型的结果进行对比,研究表明,采用等代框架法对地铁进行设计研究,在工程上是可以接受的,但是结果需要修正。张亚[6]采用EA横向几何折减法进行建模分析,发现利用EA横向几何折减法进行简化计算时,侧墙弯矩与实际有大约5%的误差。庄海洋利用弹模折减法进行建模,发现场地类别越差,基岩输入的地震动对层间位移角的影响越大[13]。同时,庄海洋对大开车站的破坏机理也进行了研究,利用弹模折减法进行建模,发现主体构件连接处在地震作用下容易发生损坏[14]。上述研究并未考虑中柱质量等效。本文在保证中柱质量不变前提下,讨论4种中柱折减方式的适用性。
2 数值模型
2.1 地下结构参数
结构横断面如图1所示。结构混凝土材料的强度等级为C35,密度为2 350 kg/m3、弹性模量为31.5 GPa、泊松比为0.2;中柱混凝土材料的强度等级为C50,密度为2 500 kg/m3、弹性模量为34.5 GPa、泊松比为0.2。结构埋深(结构顶面至地表的距离)为2.6 m,不考虑土体与结构间的接触非线性。四个柱子的尺寸均为700 mm×1 000 mm,柱距为9 m。侧墙厚度为700 mm,顶板、中板和底板厚度分别为900 mm,400 mm和1 000 mm。

二维模型将中柱简化为纵向连续墙体,在保证中柱质量不变前提下,通过折减墙体的几何尺寸或材料参数使其具有与中柱相同的截面抗弯刚度EI或抗压刚度EA,四种折减方式为:
1)EA横向几何折减,即减小墙体横向宽度来保证中柱截面EA不变,墙体宽度和质量密度分别变为0.078 m和2 493 kg/m3;
2)EI横向几何折减,即减小墙体横向宽度来保证中柱截面横向EI不变,墙宽度和质量密度分别变为0.336 5 m和577.84 kg/m3;
3)纵向几何折减,即将中柱平面应变单元厚度取为中柱纵向宽度1 m,除中柱以外的土和结构平面应变单元厚度取为纵向一跨尺寸9 m;
4)弹模折减,即减小墙体材料弹性模量E来保证中柱截面EA和EI不变,墙体的弹性模量和质量密度分别变为3.83 GPa和277.78 kg/m3。
2.2 土体参数
车站所处场地由素填土、粉质黏土、淤泥质黏土、砂黏土、强风化花岗岩组成,基岩主要是中风化花岗岩、弱风化大理岩。场地土层参数如表1所示。

表1 场地地层土性物理参数
为考虑土体的非线性,根据杜修力等[15]的研究确定场地等效材料参数。首先利用EERA场地分析得到每层土体的等效剪切模量及阻尼比,将滞回阻尼转化为瑞利阻尼,瑞利阻尼计算公式为:
C=αM+βK
(1)
其中,M,K分别为土体质量矩阵和刚度矩阵;α,β分别为质量系数和刚度系数。
2.3 地震动
车站所处场地地震安评报告中所提供的是E2水平的场地地表地震动,故用EERA程序将场地地表地震动反演到模型底部,得到的地震动加速度时程如图2所示,地震动总持时40.94 s,加速度峰值为0.050 6g。
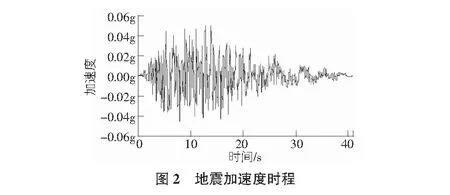
2.4 边界和初始条件
计算模型的宽度和高度分别为224 m,50 m。侧边界采用滚轴边界模拟无限域土体的自由场效应,模型底部固定。计算过程分两步,首先计算重力荷载作用下的初始应力场,作为下一个动力分析步的初始内力,动力计算时对整个土—结构模型施加水平向惯性力。
2.5 参考解
为了评价中柱简化的精度,采用三维模型计算结果作为参考解。三维有限元模型如图3所示,取中柱前后各半跨4.5 m,模型的两个截断面施加对称边界条件,其余材料和几何参数均按实际选取。

3 结果讨论
3.1 结构层间位移
结构的最大峰值位移出现在顶层,故给出结构顶层峰值位移及误差结果如表2所示,从表2可以看出与三维模型的位移结果相比,EI横向几何折减法、弹模折减法、纵向几何折减法的最大峰值位移误差较小,而EA横向几何折减法的峰值位移误差较大,故不推荐EA横向几何折减法,此后不再讨论此方法。

表2 结构顶层峰值位移及误差
3.2 构件截面的平均压应力
构件截面的平均压应力如图4所示,平均压应力误差如表3所示。

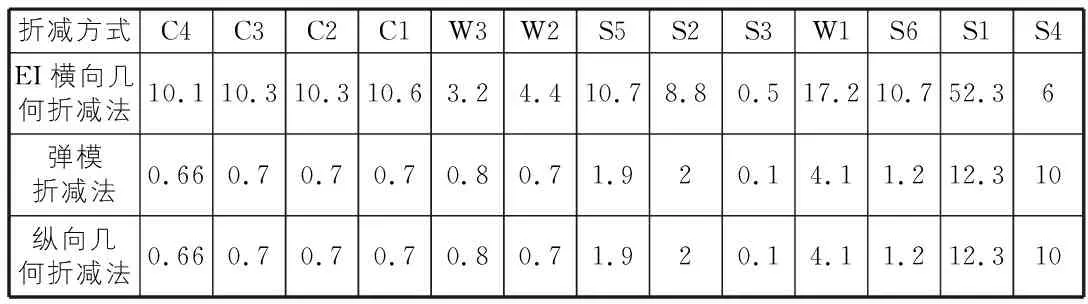
表3 平均压应力误差 %
3.3 构件截面的平均剪应力
构件截面的平均剪应力及其误差见图5,表4。


表4 平均剪应力误差 %
3.4 构件截面的最大拉应力
构件截面的最大拉应力及其误差见图6,表5。
接下来讨论二维模型建模方式的平均应力结果,讨论截面位置见图1。以三维模型为例,对所有截面的平均压应力、平均剪应力和平均最大拉应力分别按照从大到小的顺序进行排序,结果如图4~图6所示。以三维模型的平均应力为参考解,将其余二维模型的平均应力与之对比,得到所有截面的平均应力误差,如表3~表5所示。三种截面应力分别取大小排名前三的截面误差进行分析,弹摸折减法和纵向几何折减法这两种方法的误差均小于EI横向几何折减法。就平均压应力而言,前两种方法的误差范围为0.66%~0.7%,EI横向几何折减法的误差范围是10.1%~10.3%。就平均剪应力而言,前两种方法的误差范围为0.6%~11.9%,EI横向几何折减法的误差范围是2.4%~53.7%。就最大拉应力而言,前两种方法的误差范围为0.7%~12.3%,EI横向几何折减法的误差的范围是2.7%~57.7%。


表5 最大拉应力误差 %
4 结论
本文以某两层三跨地铁车站的地震响应分析为工程背景,将EI横向几何折减法、EA横向几何折减法、纵向几何折减法和弹模折减法都考虑中柱质量等效原则对二维模型中柱材料的密度进行折减,通过与三维模型的数值结果对比,分析了以上四种处理方法的精度,得出以下结论:
1)与三维模型的位移结果相比,EI横向几何折减法、弹模折减法、纵向几何折减法的最大峰值位移误差较小,而EA横向几何折减法的峰值位移误差较大,故不推荐EA横向几何折减法。2)研究发现,弹模折减法和纵向几何折减法这两种方法的平均应力误差较小,平均应力误差为0.6%~12.3%,因此推荐工程使用。综上所述,在进行地铁车站的中柱简化时,本文推荐使用弹模折减法和纵向几何折减法。

