带花纹轮胎仿真模型建立及影响因素研究

姜洪旭，王海艳，刘昌波

[1.浦林成山（青岛）工业研究设计有限公司，山东 青岛 266011；2.浦林成山（山东）轮胎有限公司，山东 荣成 264300]

自20世纪70年代有限元方法开始在轮胎设计中得到广泛应用[1]，但由于花纹结构的复杂性和计算机能力的限制，长期以来轮胎仿真没能将胎面花纹考虑进去，直到2000年才出现有关带花纹轮胎抗湿滑性能的仿真研究[2]，之后出现了涉及轮胎六分力、雪地性能和耐磨性能的仿真研究[3-5]。

国内研究人员采用子模型和组合模型技术实现了轮胎花纹静负荷接地性能仿真，其仿真结果与试验结果十分接近，并在此基础上开展了轮胎花纹对轮胎内部受力以及带花纹轮胎的稳态滚动和显示滚动的研究[6-7]。由于轮胎花纹结构复杂，使得原来就很复杂的轮胎有限元仿真更加困难，自从Meschke和Shiraishi使用组合模型技术（即将花纹与轮胎其他部分分开建模，如图1所示）以来，该技术一直沿用至今。

有限元网格质量关系到模型的收敛性和计算精度，获得较高的网格质量是轮胎花纹有限元建模的一个挑战。目前主要有两种轮胎花纹有限元建模方法。一种是基于映射和拉伸，将网格划分好的花纹展开图通过坐标变换得到轮胎花纹有限元分析模型。其优点是网格质量能得到保证，建模效率较高，缺点是花纹模型有些失真。另一种是应用CATIA和UG等三维造型软件完成轮胎花纹几何建模，然后用Hypermesh进行网格划分。其优点是可以保证花纹几何形状的真实性，缺点是过程比较繁琐。本工作采用第2种建模方法研究带花纹轮胎的仿真建模。

1 花纹模型建立

Abaqus带花纹轮胎建模有两种方法：一种是建立完整的花纹模型和完整的轮胎其他部分模型，然后将两者组合生成完整模型（如图2所示）；另一种是建立单节花纹块和对应的轮胎其他部位模型，将两者组合，再沿圆周方向拓展生成完整模型（如图3所示）。两种建模方法在几何结构上可以做到完全一样，因此对于接地印痕分析，两者不会有任何差异。本研究采用后一种方法实现带花纹轮胎的稳态滚动分析。

图2 建立完整花纹组合式轮胎模型示意

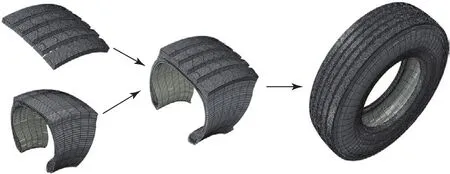
图3 建立单节花纹组合式轮胎模型示意

Abaqus稳态滚动分析采用的是拉格朗日-欧拉混合描述。拉格郎日描述是指单元节点与材料固定在一起，网格随着材料运动而变形；欧拉描述是指网格几何形状固定而材料在网格内部运动。在Abaqus中轮胎的稳态滚动是通过材料在网格内部的流动来模拟，欧拉描述的要求是材料流动的流线必须是连续的，而考虑花纹时，由于横向花纹沟的存在，流线被破坏，无法完成滚动的模拟，解决这个问题的方法是建立周期性的模型[8-9]。

轮胎花纹几何模型根据我公司T116A花纹图在CATIA中完成建模，如图4所示。

图4 轮胎花纹在CATIA中建模示意

轮胎花纹的3D模型建立基本与模具一致，但基于保证后续网格的质量，以利于计算时的收敛性和提高建模、计算效率，仍对花纹结构进行某些简化处理，如忽略了钢片、变沟深设计等。为了获得较高求解精度和网格质量较好的六面体网格，花纹网格的划分在Hypermesh中完成，见图5。

图5 轮胎花纹网格示意

2 模型验证

2.1 接地印痕

轮胎接地印痕仿真和测试结果见图6。

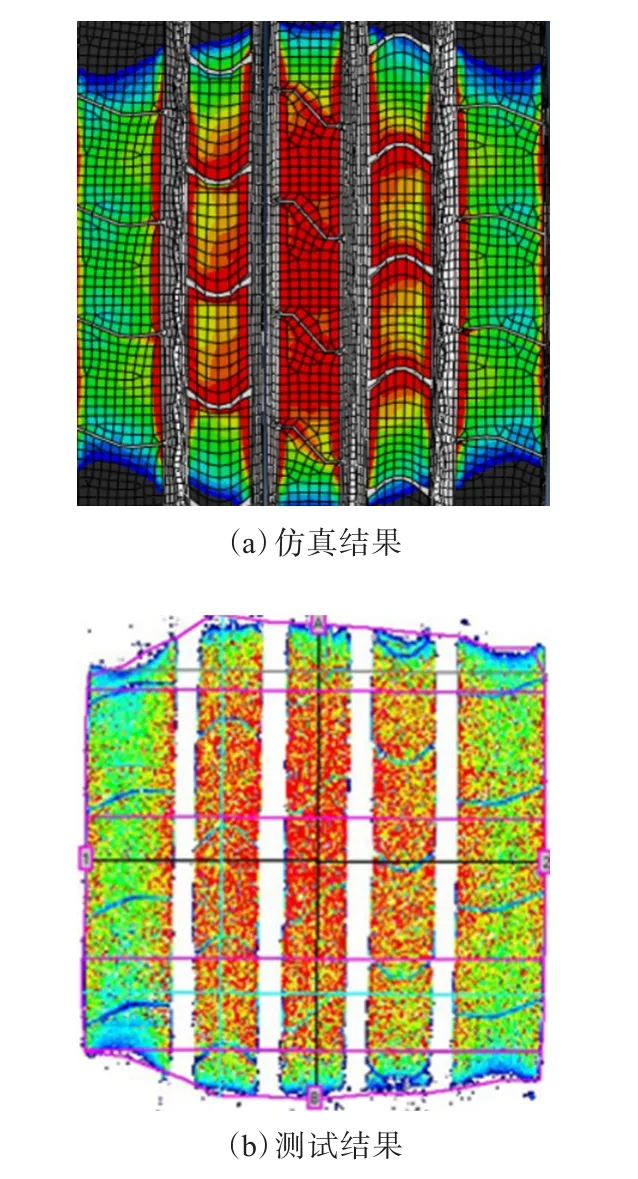
图6 轮胎接地印痕仿真和测试结果

由图6可以看出，带花纹轮胎的仿真接地印痕形状与实测形状接近，仿真准确度很高。

2.2 稳态滚动仿真的合理性验证

Abaqus-Standard求解非线性问题采用牛顿-拉普森法求解平衡方程，在分析过程中，将负荷分解成很多小的增量，每个增量的施加过程都需求解平衡方程，以达到稳定状态。因此，轮胎侧偏、侧倾的稳态仿真的过程是一个稳态过程，这样就可以运用汽车动力学中车轮稳态滚动卡姆圆公式来验证仿真结果是否合理[10]。

车轮稳态滚动卡姆圆公式如下：

式中，Fx为轮胎纵向力，Fy为轮胎侧向力，μ为轮胎附着因数，Fz为负荷。

根据上述公式可得到稳态滚动纵向力与侧向力的关系。当轮胎稳态滚动时，纵向力的增大会带来侧向力的减小，仿真结果见图7，其与理论预测趋势一致，说明仿真结果具有合理性。

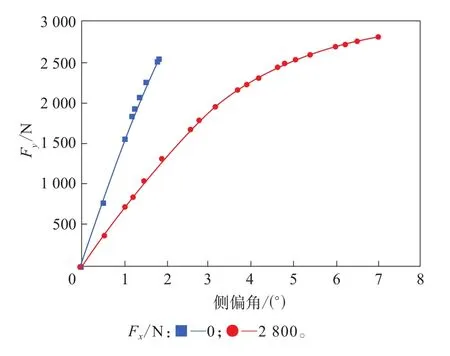
图7 轮胎稳态滚动侧向力与纵向力的关系

3 仿真结果分析

汽车动力学中，关于侧向力-侧偏角特性都是适用于稳态的，即考察特性曲线时，侧偏角是确定的，不随时间变化，否则侧偏特性关系将不再成立。轮胎侧偏测试分为稳态测试和瞬态测试，稳态测试是为了匹配车辆悬架，满足操纵性能的要求；瞬态测试是为了了解极限情况下轮胎性能的可靠性，例如通用汽车公司对轮胎力和力矩的测量就是稳态测量。

本研究通过轮胎的稳态滚动仿真，确定轮胎自由滚动状态后，对轮胎施加侧偏角和侧倾角，从而获得动态接地印痕和六分力特性曲线。

3.1 动态接地印痕

在轮胎达到自由滚动状态后，给轮胎施加侧偏角得到的动态接地印痕如图8所示。仿真与试验结果具有相同的趋势，即随着侧偏角的增大，接地印痕一侧接地压力和接地长度增大。

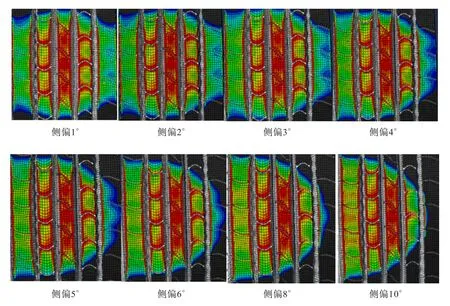
图8 轮胎不同侧偏角下的动态接地印痕

3.2 花纹对轮胎侧偏和侧倾特性曲线的影响

花纹对轮胎侧向力和回正刚度的影响分别如图9和10所示。

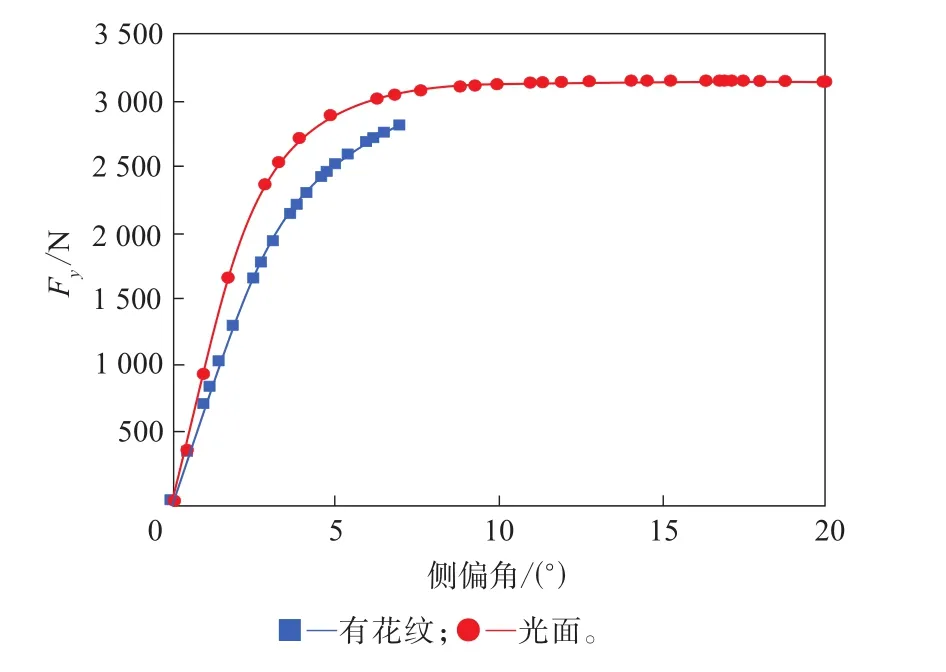
图9 花纹对轮胎侧向力的影响

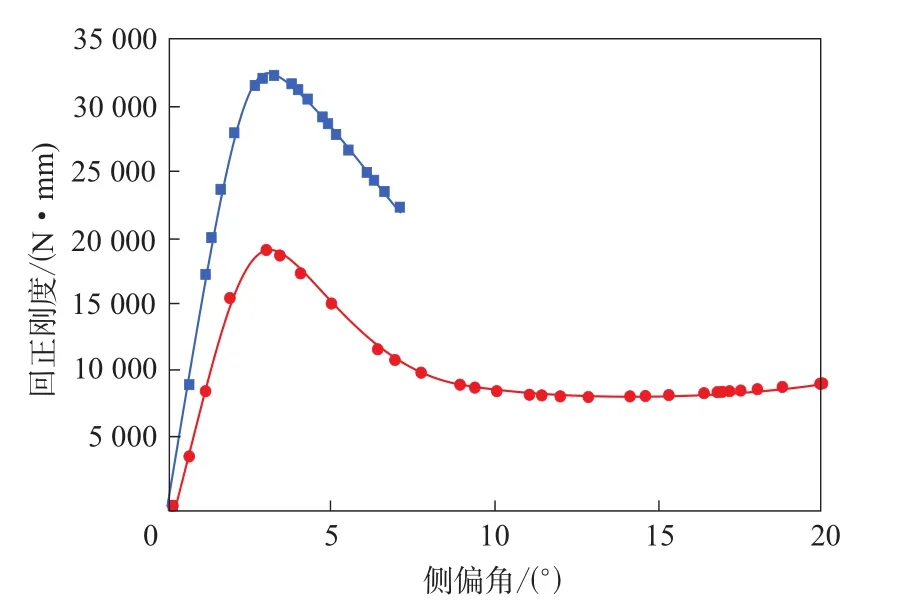
图10 花纹对轮胎回正刚度的影响

由图9和10可见，花纹对轮胎侧偏和侧倾特性影响明显，考虑花纹后，侧向力相比光面轮胎减小，回正刚度则增大。

3.3 路面对轮胎侧偏和侧倾特性曲线的影响

轮胎的六分力试验机分为转鼓式和履带式两种，见图11。本研究通过仿真分析对比两种路面对轮胎六分力的影响，在Abaqus中建立直径为1.7 m的转鼓和平直路面，将两者均设为刚体，如图12所示。路面对轮胎侧偏和侧倾特性曲线的影响如图13—16所示。

图11 六分力试验机

图12 两种仿真路面

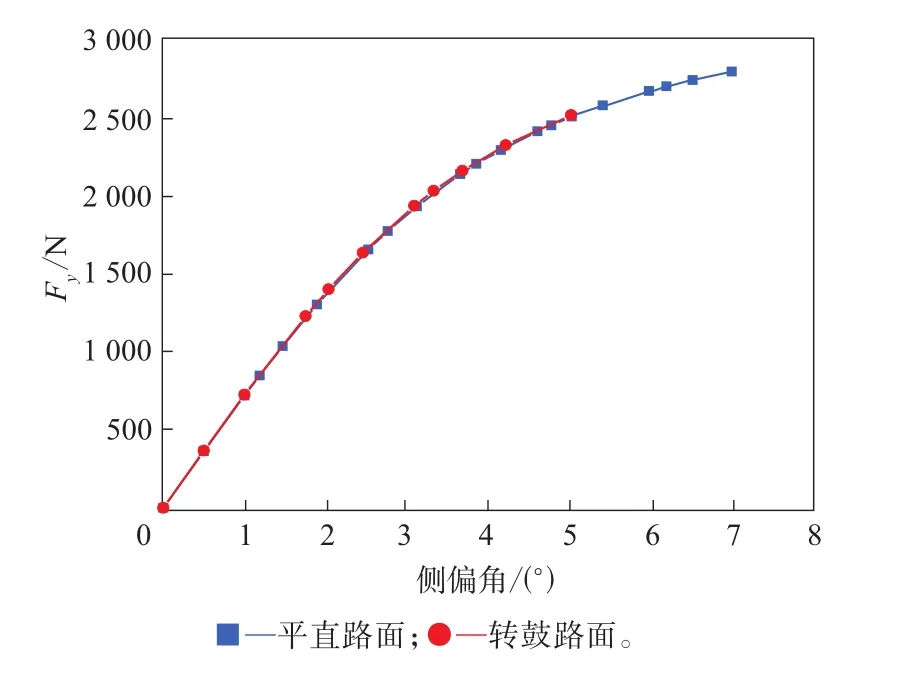
图13 路面对轮胎侧向力-侧偏角曲线的影响

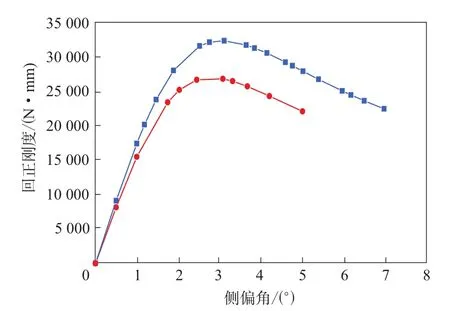
图14 路面对轮胎回正刚度-侧倾角曲线的影响

图15 路面对轮胎侧向力-侧倾角曲线的影响

图16 路面对轮胎回正刚度-侧倾角曲线的影响

由图13—16可知：转鼓和平直路面的侧偏特性曲线几乎没有差异，而回正特性曲线则明显不同，平直路面上的回正刚度和最大回正力矩大于转鼓路面；侧倾特性曲线也有相同规律，侧向力在平直路面和转鼓路面上相差不大，侧倾力矩在平直路面上要明显大于在转鼓路面上。

3.4 轮胎力和力矩稳态测试项目仿真

根据通用汽车公司轮胎力和力矩测试项目[11]，采用有限元仿真得到六分力曲线进而处理得到其要求的数据，轮胎规格为225/40R18。

转向因数（μc）计算公式如下：

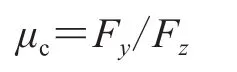
侧偏角为1°时，μc＝2 152.74/6 300＝0.34。

回正刚度因数（μA）计算公式如下：

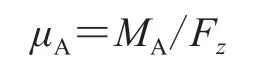
式中，MA为回正力矩。

侧偏角为1°时，μA＝61 948.1/6 300＝9.83。

负荷灵敏度函数（H）计算公式如下：

侧偏角为1°时，H＝（2 152.74－1 916.84）/1 260＝0.187。

负荷传递灵敏度函数（G）计算公式如下：

式中，P为负荷，α为侧偏角。

当侧偏角为4°时

4 结论

（1）带花纹轮胎仿真模块静负荷接地印痕精度达到90%以上，接地印痕仿真结果与实测结果十分接近。

（2）完成了带花纹轮胎静负荷接地印痕、稳态滚动、稳态侧偏和侧倾仿真功能开发，可获得带花纹轮胎六分力曲线，预测动态接地印痕。