基于相关向量机的富水砂层渣土改良试验效果预测

张 研，梁卓悦，廖逸夫

(1.桂林理工大学广西岩土力学与工程重点实验室，桂林 541004；2.桂林理工大学土木与建筑工程学院，桂林 541004)

随着中国城镇化的发展，城市人口数量逐渐增多，交通拥堵问题日益突出，许多城市通过修建地铁来缓解交通压力。盾构法由于具有施工效率高、对地面结构影响小、施工质量高等优点被广泛应用于地铁隧道施工[1]。然而盾构法在富水砂层掘进时，需采用渣土提前对土体进行改良，以提高砂土的抗渗透能力、可塑性，从而降低该种不良地质情况下盾构施工的安全风险。

富水砂层具有灵敏度高、易塌陷、受力弱的缺点，采用渣土对其进行改良时，改良效果的精准掌握可为施工方案的及时调整提供重要参考依据。因此，很多学者多采用塌落度、渗透参数和内摩擦角3个参数对改良效果进行评价，王明胜等[2]以成都地铁7号线作为研究对象，分析不同改良剂对盾构掘进参数的影响，选出最好的改良剂配方；陈先智等[3]以昆明地铁4号线土样作为研究材料，研究表明聚丙烯酰胺溶液加到泥浆中时，能提高渣土坍落度；王树英等[4]研究渣土改良中水压力的影响，发现当水压力超过一定值后，渗透性不能满足规定要求；陈中天[5]研究颗粒级配对改良效果的影响，并修正了泡沫注入率公式；孙欣欣[6]通过直剪和正交实验对不同的泥浆配制方案进行评价，得出一个最佳改良方案。

目前，渣土改良效果评价的3个参数多是通过室内土工试验获取，室内试验存在周期长、成本高等不足，寻求更加快速、经济的方法对渣土改良效果进行评价为学者所关注。随着智能科学的发展，有学者采用反向传播(back propagatio，BP)神经网络对富水砂层改良效果进行预测[7]，为富水砂层改良效果评价提供一条新思路。然而神经网络也存一些不足，如：在训练数据过少时模型精度难以保证；样本过多时，模型泛化能力明显降低。因此，更加准确、合理的机器学习模型亟待提出。

近年来兴起的相关向量机(relevant vector machine,RVM)是一种基于贝叶斯理论、马尔科夫性质、自动相关决定先验和最大似然理论方法的一种机器学习方法[8]，由于其具有准确率高、偏离度低等优点，现已被运用到许多复杂工程问题中。现将RVM应用于富水砂层渣土改良效果预测，提出基于相关向量机的富水砂层渣土改良试验效果预测模型，并将该模型与BP神经网络模型及实测值进行比较分析，为富水砂层渣土改良试验效果评价提供一条新途径。

1 RVM相关理论

相关向量机在选取核函数时不受Mercer条件的约束，能做到二值和概率输出，且运行速度快[9]，设训练数据样本为{xn,tn|n=1,2,…,N}，xn为输入值，tn为输出值，N为数据样本数量，回归模型的表达式为

(1)

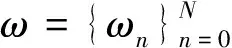
p(tn|xn)=N(tn|y(xn),σ2)

(2)

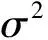
(3)

式(3)中：t=(t1,t2,…,tN)T；ω=(ω0,ω1,…,ωN)T；Φ=[φ(x1),φ(x2),…,φ(xN)]T是N×(N+1)矩阵，矩阵中的每列的表达式为φ(xn)=[1,k(xn,x1),k(xn,x2)],…,k(xn,xN)]T，引入超参数α=(α0,α1,…,αN)T对式(3)中的ω和σ2进行求解，ωn满足高斯分布，其表达式为

(4)

预测数据集的输入值x*和输出值t*具有的表达式为

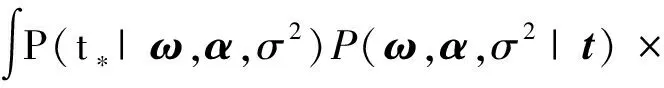
dωdαdσ2

(5)

根据贝叶斯和马科夫性质与式(5)联立简化可得

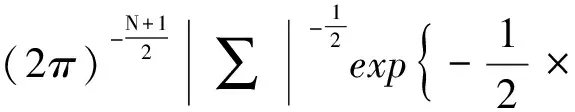
(6)

协方差的表达式为

∑=(σ2ΦTΦ+A)-1

(7)

权重均值的表达式为

μ=σ-2∑ΦTt

(8)

A=diag(a0,a1,…，aN)

(9)

最大似然函数经过整理简化后可由式(10)表达为

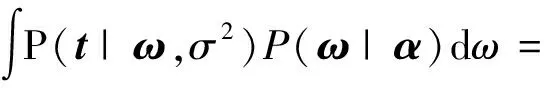
(10)

经过分别对式(10)的α和σ2求偏导数，令其值为0，建立两个方程，经简化可得

(11)

(12)

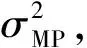
y*=μTφ(x*)

(13)

(14)

式中：x*为待预测样本；y*为输出值t*的均值。

2 实例分析

2.1 富水砂层渣土试验数据

富水砂层渣土改良效果受多种因素影响，各影响因素之间关系错综复杂[10]，为了准确高效预测渣土改良效果，输入的变量和种类对模型预测非常重要，根据中外相关研究，综合考虑数据获取的难易程度，选取了渗透系数、内摩擦角(改良前)、电阻率、泡沫剂浓度和膨润土浓度5个影响因素作为相关向量机模型的输入变量，选取坍落度、渗透系数、内摩擦角(改良后)作为输出变量[7]。根据相关向量机的原理，建立了RVM模型如图1所示。

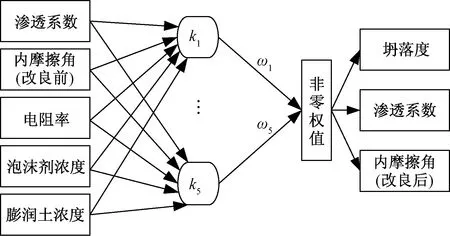
k1,k2,…,k5分别为第一到第五个核函数；ω1,ω2,…,ω5分别为第一到第五个核函数的权重值

运用MTALAB软件编制相关向量机程序，建立RVM预测模型，引用文献[7]中的数据，选择与文献[7]相同的学习样本和预测样本，40组数据如表1所示，前24组为训练集，中间8组为验证集，后8组为预测集。

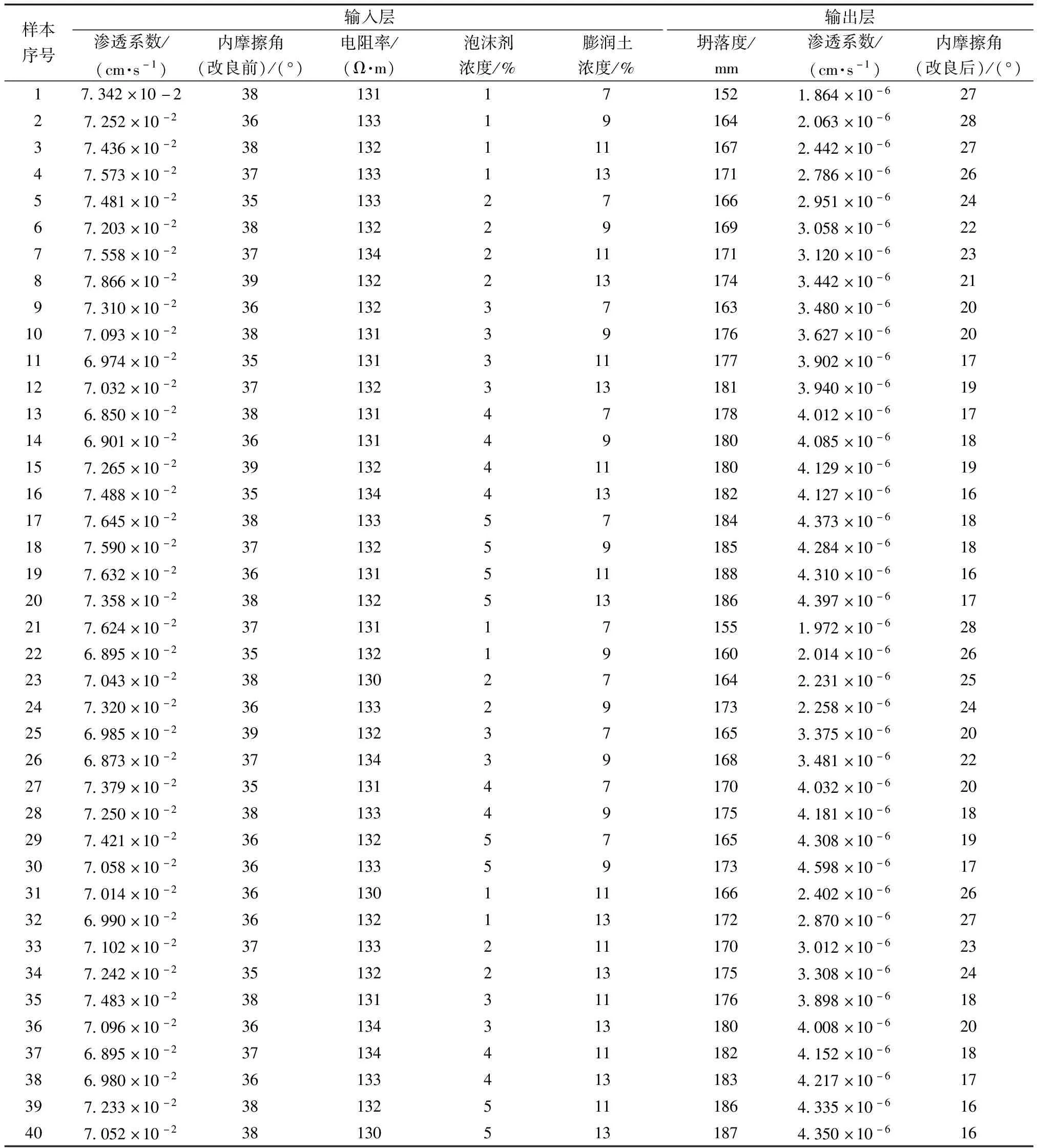
表1 数据样本集

2.2 方法与实现步骤

步骤一归一化处理。由于输入层及输出层数据的数量级差异很大，为了使数据更方便统计和提高模型预测精度，将40组数据进行归一化处理。

(15)

(16)

式中：Xk,i为第k个因子的第i个数据值，当k取1、2、3、4、5时分别代表渗透系数、内摩擦角(改良前)、电阻率、泡沫剂浓度和膨润土浓度；Xk,min和Xk,max分别为不同因素中数据的最小值和最大值；X′k,i为归一化处理过后第k个因子的第i个数值；Yk,i为第k个因子的第i个输出值；Yk,max和Yk,min分别为不同输出变量的最大值和最小值；Y′k,i为归一化处理后第k个影响因素的第i个数值。

步骤二分类。把经过归一化处理的数据，分成三部分：训练样本数据集、验证样本数据集和预测样本数据集，训练集用于模型拟合训练，验证集用于调整模型参数，预测集用于检测模型预测的效果。

步骤三选取函数。整理分析得到的结果，根据结果选取更适宜的核函数、参数，并确定最大的迭代次数。

步骤四调整。不断调整核函数和相关参数，优化拟合结果，把预测样本数据集输入模型中，分析预测的结果，检验模型的可靠性。

2.3 RVM相关向量机预测模型效果分析

将8个预测样本数据输入模型后得出预测结果，预测坍落度和渗透系数的误差均不超过1%，其中对渗透系数的第8个样本预测误差仅为0.029%。RVM与BP神经网络的预测效果对比如图2所示。

从图2(a)～图2(c)可直观看出，RVM预测精度更高，它预测出的结果几乎与实测值重合，在坍落度的第8个预测样本、渗透系数的第2个预测样本和内摩擦角的第2个预测样本可看出BP神经网络的预测值偏离实测值较大，说明BP神经网络预测不稳定，有些数据预测偏差达10%以上，但RVM的预测误差绝对值最大仅为4.06%。为了进一步验证RVM模型的优势，计算出不同预测指标的最大误差、最小误差和平均误差，结果如表2所示。

图2 不同预测方法的预测值与实际值对比

由表2可知，RVM模型在预测富水砂层渣土改良效果比BP神经网络更具有优势，预测精度更高。RVM模型在预测坍落度、渗透系数、内摩擦角时的相对误差的平均值分别为0.73%、0.38%和2.24%，而BP神经网络预测的平均误差分别为1.76%、4.53%和3.60%，从最大误差来看，RVM模型最大误差分别为0.79%、0.74%和4.07%，而BP神经网络预测的最大误差分别为2.14%、10.73%和12.50%，通过对比两种模型的最大误差和平均误差，说明RVM模型有预测精度高、预测稳定的优点[11]。

表2 不同预测模型预测结果对比

3 相关系数分析

研究两组数据的相关性时，可采用皮尔逊相关系数[12]，用皮尔逊相关系数r分析RVM模型、BP神经网络模型与实测值的相关性，通过r可直观反映出这两种模型的预测值与实测值的相关性。r>0说明两个数据成正相关，r越大，则两组数据的相关性越强。

协方差计算公式为

Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}

(17)

Pearson系数计算公式为

(18)

式中：Xi为不同预测方法的预测值；Yi为实测值；E(X)和E(Y)为平均值，也称为期望值；Cov为协方差；σ为标准差。根据式(17)和式(18)可计算出相关系数，如表3所示。

从表3可知，RVM模型与实测值的相关性分别为0.999 9、0.999 3和0.987 8，而BP神经网络模型与实测值的相关性分别为0.967 7、0.953 4和0.902 3，说明RVM模型相比于BP神经网络模型的预测结果与实测值的相关性更高，稳定性更好，由此可知，RVM模型能为富水砂层渣土改良试验效果的预测提供一种新方法。

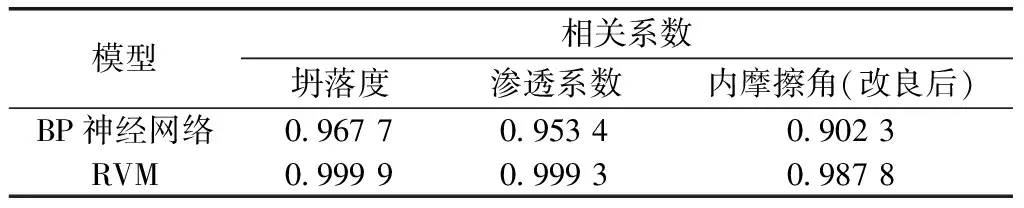
表3 不同预测模型的皮尔逊相关系数对比

4 结论

建立了基于相关向量机的富水砂层渣土改良试验效果预测模型，并通过用24组为训练集、8组验证集、8组预测集，完成选取核函数、参数和确定最佳迭代次数等模型优化工作，最后得出的预测结果令人满意，经过与BP神经网络模型的对比分析，得出结论如下。

(1)实例表明，RVM模型比BP神经网络模型在富水砂层渣土改良效果预测中更具优势，说明了RVM模型可基于小样本数据做到高精度的预测。

(2)通过皮尔逊相关系数计算，可知RVM模型的预测值与实测值有很强的线性相关性，预测值离散度小，在实际工程中能为施工方案的及时调整提供重要参考依据。

(3)可通过增加训练集、验证集和预测集的数据量使RVM模型的预测结果更具有说服力，另外可把RVM模型推广到其他实际工程中解决复杂问题。