贵州省本地化温度客观订正算法探究

孔德璇，杨春艳，朱文达，唐浩鹏

(1.贵州省黔西南布依族苗族自治州气象局，贵州 兴义 562400；2.贵州省气象台，贵州 贵阳 550002)

0 引言

十三五规划中就已经提出了“无缝接预报预警”的工作规划和要求，着力构建以信息化为基础的无缝隙、精准、智慧监测预报预警业务。目前贵州省智能网格业务已初具雏形，但离“无缝隙、精准”的精细化预报要求还有一定的差距，原因是缺少改善要素预报准确率的核心技术方法。随着数值天气预报模式水平的不断提高，数值模式天气预报已逐渐成为了全国各级气象台站预报业务重要的技术支撑，它的要素预报也成为了预报业务的重要参考依据。尽管如此，相对于形势预报来说，要素预报的性能仍旧不能满足目前“无缝隙、精准”的精细化预报业务要求。

目前，从数值预报的初始扰动方案、物理过程参数化、资料同化等方面即从数值模式预报本身直接来改善要素场预报是十分困难的，且所需要的实验周期相对于实际业务发展和应用来说是十分漫长的。由于数值模式初始设置的不确定性，使得数值模式本身一定存在系统性的误差[1-2]。采用一些后处理的订正方法(数值预报释用技术)对数值模式输出的产品进行订正是十分必要的[3]，这样做就能缩短计算实验周期，在短时间内改善数值预报的要素场预报性能。

为此，国内外的学者和专家针对要素预报的订正方法做了许多相关的研究：李佰平等[4]使用线性回归、单时效消除偏差和多时效消除偏差平均等订正方法，对模式地面气温预报订正，有效的提高了预报准确率，并证明在模式预报误差较大的情况下，多时效集成的订正方法能稳定的减小误差。滑动平均、多模式动态权重、历史偏差等方法被一些学者用来构建温度预报的订正方案，均取得了不错的效果，同时发现滑动平均和历史偏差方法的最优训练期是25～30 d[5-7]。虽然这些订正方案可以获得较好的订正效果[8-11]，但具有计算量大、训练期长和所需历史资料序列长的特点，业务化过程中具有相当的局限性。

经过许多知名专家和学者的探索发现类卡尔曼滤波、卡尔曼滤波、频率匹配以及多模式集成等方法具有计算量小，所需资料序列短的优势，且对模式要素预报有着更为显著的订正效果，对气温预报、地面温度预报、降水预报都具有应用和参考价值[12-19]。另外一方面，机器学习和深度学习方法也被用于做要素预报的订正，如王焕毅等人[20]采用BP神经网络建立本地化的温度预报客观订正算法，对3种数值模式进行了订正，系统偏差和均方根误差明显缩小，提高了气温预报准确率。Dongjin Cho等[21]采用随机森林法(RF)、向量回归(SVR)、人工神经网络(ANN)和多模式集成(MME)来订正本地模式(LDAPS韩国本地NWP模式)输出的最高和最低温度，取得了不错的订正效果。Chang-Jiang Zhang[22]使用长短期记忆网络(LSTM)构建降水订正客观算法模型，对ECMWF模式中国东部的降水进行订正，有效的减少了均方根误差。

本文旨在寻找适用于贵州省的模式温度预报客观订正算法，建立起本地化的温度客观订正算法，基于时间持续偏差和类卡尔曼滤波递减平均统计降尺度两种方法，构建贵州省模式温度预报客观订正算法模型，对欧洲中期天气预报中心(ECMWF)2m温度预报进行试验性预报和检验对比分析，以期能够建立起具有一定参考价值的温度预报客观订正算法模型。

1 资料和方法

1.1 资料

模式资料：中国气象局通过卫星广播下发的Micaps资料，其中的欧洲中期天气预报中心(ECMWF)20时起报的2 m温度预报。所选时段为2019年4月1日—7月31日，区域为10～60°N，70～140°E，资料的水平空间分辨率为0.125°×0.125°，预报时效为0～240 h，0～72 h间隔时间为3 h，72～240 h间隔时间为6 h。

观测资料：贵州省364个气象自动观测骨干站点对温度的小时观测值，所选时段为2019年4月1日00时—7月31日23时。

1.2 方法

预报性能评估方法，为综合衡量原始模式和订正预报的预报能力，下面综合应用平均绝对误差MAE和平均误差ME对订正预报和原始数值预报进行评估。MAE和ME计算见式(1)和式(2)：

(1)

(2)

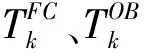
时间持续偏差订正(滑动平均)：统计模式预报的持续系统性偏差，计算出模式预报在过去n天的误差(ME)，据此来订正最新模式预报，单站订正结果计算见式(3)，Tt即为单站某预报时效下对模式的订正预报。

(3)

使用类卡尔曼滤波递减平均统计降尺度方法对观测数据进行滤波，寻找出观测资料和预报资料的系统偏差，具有自适应和计算量小的特征，适合实际应用[12]。具体构建的递减平均降尺度统计函数见(4)式和(5)式。

MEt0=MEt-1(1-w)+MEt×w

(4)

(5)

2 时间持续偏差订正方案及效果评估

时间持续偏差的时效滑动平均订正方案：取前n次相同预报时效下的平均误差即滑动平均误差，滑动训练期分别取n=3、n=5和n=7。用模式预报减去滑动平均误差，可得到订正预报的值。

时间持续偏差的滚动订正方案：以模式预报时刻为时间起点，按照预报产品既定的时间间隔向前n个时刻(本时次的预报产品不足则采用上一时次的来补足)滑动训练预报的平均误差，训练期分别取n=3、n=5和n=7。用该模式预报减去训练出来的滑动平均误差，可得到订正预报的值。

分别使用上述两种订正方案对ECMWF模式2019年7月1日—15日20时起报的2 m温度进行订正，使用区域和时间平均绝对误差(MAE)对不同的订正预报和原始预报进行对比分析，由于考虑业务应用的资料周期和计算量问题，滑动训练期只取了3 d、5 d和7 d，除了极少数站点，大多数站点的订正效果不好，不同滑动训练期下两种订正预报的平均MAE均比原始预报的要大，但可以看出除了一些特殊的预报时效外，其余大多数预报时效下的时效滑动平均订正方案要比滚动订正方案效果好(见图1)。

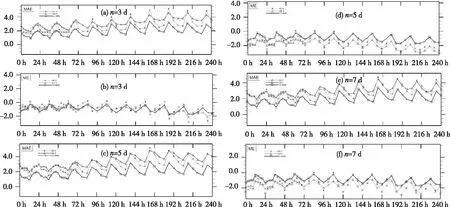
图1 不同滑动训练期下两种时间持续偏差订正预报与原始ECMWF模式2 m温度预报的绝对平均误差(MAE)和平均误差(ME)分析图(a、b滑动训练期为3 d，c、d滑动训练期为5 d，e、f滑动训练期为7 d)

3 类卡尔曼滤波的递减平均统计降尺度订正方案及效果评估

递减平均统计降尺度方法是通过统计历史预报和实况值之间的误差，订正模式预报产生的误差，使得预报更加接近观测值。

递减平均统计降尺度法的初始化偏差MEt-1有偏差“热启动”和偏差“冷启动”两种方式：偏差“热启动”是用过去一定天数的偏差值的时间平均值作为初始化偏差MEt-1的值；偏差“冷启动”即将初始值直接设为0，在资料序列不足的情况下可采用这种方法，起到便于计算的作用。

为了取得较好的预报效果，考虑到资料序列短，计算量小的业务化需求，本文采用“热启动”的方式来计算初始化偏差值MEt-1，递减平均统计降尺度的偏差训练期为30 d。

在真正对模式预报进行订正之前需要做w参数的敏感性试验，即找出订正效果较好的w参数。按照区域位置选取全省10个代表站进行w参数的敏感性试验，w分别取0.2～0.9之间的15个参数(间隔0.05)来进行敏感性实验。

经计算，w在取0.40和0.85附近时，平均绝对误差(MAE)很小，故取0.40、0.45、0.85来分别构建订正方案对2019年7月1—15日ECMWF模式的2m温度预报进行订正。计算出订正预报后，筛选出订正效果较好的站点利用MAE和ME对订正预报和原始预报的预报能力进行评估。无论是哪种参数方案，均取得了不错的订正效果，MAE在大多数时效下均比原始预报要小。3种参数方案下平均绝对误差MAE缩小了0.36、0.37和0.43，其中72 h内订正效果十分显著，MAE分别缩小了0.62、0.63和0.72。但无论是原始预报还是订正预报，随着预报时效的增加，MAE大体呈现出波动式的增长趋势(见图2)。

图2 不同w参数方案下的递减平均统计降尺度订正预报与原始ECMWF模式2m温度预报的绝对平均误差(MAE)和平均误差(ME)分析图a、b w参数为0.40，c、d w参数为0.45，e、f w参数为0.85)

为了更加真实准确地反映出每一种参数方案下的订正预报和原始ECMWF模式2 m温度预报的整体情况，针对不同参数方案下的预报效果较好的站点，对其订正预报和原始预报分别与观测值做散点图来分析订正预报和原始数值预报的预报能力(见图3)。

图3 不同参数方案下(所筛选出预报效果较好的站点不同)订正预报与原始ECMWF模式2 m温度预报分别与观测值的散点图，图中不同颜色代表不同范围段的预报及相应观测值的联合概率密度函数(PDF，单位为:%)；a、b为w=0.40时订正预报a与原始ECMWF模式2 m温度预报b散点图；c、d为w=0.45时订正预报c与原始ECMWF模式2 m温度预报d散点图；e、f为w=0.85时订正预报e与原始ECMWF模式2 m温度预报f散点图

无论是哪种参数方案下的订正预报整体上均更加接近于实况观测值，订正预报的整体准确程度是优于原始预报的，联合概率密度大值区域的中心更加接近于对角线，即订正预报更加接近观测值的次数要比原始数值预报多，尤其是w=0.45参数方案下的订正预报更为明显。但所有方案下相应站点中原始数值预报的联合密度区域更加集中，也就是说订正算法使得预报的离散程度更大了。可以看作是将原始预报同时向更好和更差的两个方向订正了，有一部分预报仍然是做了负订正，说明了订正预报的算法方案上仍然是有改进的空间的。

4 单站最优w订正方案及效果评估

为了获得更好的预报效果，在原本递减平均统计降尺度的方案上增加对参数w的训练方案：按照原本方案同时计算得出15种w参数下近期单站订正预报，按照MAE来筛选出该站点的最优w。这样的话每个站点都有属于自己最优的w参数方案，订正方案的针对性变得就更强了。

同样地，首先需要对用于评估单站w最优参数的订正预报产品数量做敏感性实验，经计算，发现3 d附近左右是最合适的，虽然预报产品的日数越长，评估出来的最优w越稳定，但由于获得的效果差距很小，且计算量明显增大了。所以这里采用3 d作为评估单站最优w参数的订正预报产品日数。

采用单站最优w方案对2019年7月1—15日ECMWF模式的2 m温度预报进行订正。同样地对计算结果筛选出订正效果较好的站点利用MAE和ME对订正预报和原始预报的预报能力进行评估(见图4)。

图4 单站最优w订正预报与原始ECMWF模式2m温度预报的绝对平均误差(MAE)和平均误差(ME)分析图：(a)MAE对比分析图；(b)ME对比分析图

单站最优w方案的订正预报取得了更为优异的订正效果，MAE比原始预报缩小了0.47，比之前3种参数方案的MAE都要小，较之前最优的方案w=0.85时的MAE再次缩小了0.04。虽然72 h内的MAE比起之前w=0.85的方案效果略微差了一点，但仍旧是比原始预报缩小了0.66。且单站最优方案在ME上面的表现是比其它方案要好的。

使用散点图分析单站最优w方案订正预报和原始数值预报的预报性能(见图5)。比起之前的订正方案，联合概率密度(PDF)大值区域的中心不仅接近于对角线，而且变得更加集中，大值中心的最大值也增大了。这意味着新的单站最优w方案将预报向更准确的方向订正了，且整体离散程度更小了，简单说来也就是预报更接近观测值的次数变多了。

图5 单站最优w参数方案订正预报与原始ECMWF模式2 m温度预报分别与观测值的散点图，图中不同颜色代表不同范围段的预报及相应观测值的联合概率密度函数(PDF，单位为:%)：(a)单站最优w参数方案订正预报；(b)相应站点的 ECMWF模式2 m温度预报

5 结论与探讨

①在较短资料序列和简单的滑动训练方案下，订正预报的表现较差，不具有参考价值。

②基于类卡尔曼滤波递减平均统计降尺度方法构建的订正方案效果是明显的，参数分别取w=0.40、w=0.45、w=0.85时部分站点的订正效果具有较高的参考价值，较原始预报(2019年7月1—15日ECMWF模式的2m温度预报)的MAE分别缩小了0.36、0.37和0.43，其中72 h内订正效果十分显著，MAE分别缩小了0.62、0.63和0.72。但无论是原始预报还是订正预报，随着预报时效的增加，MAE大体呈现出波动式的增长趋势。

③改进后的单站最优w订正方案在取得了更加优异的预报效果的同时(MAE缩小了0.47)，有效地改善了预报整体的离散程度，提高了整体的订正效果和性能，针对部分站点来说，在预报业务上具有很好的参考价值。

④基于类卡尔曼滤波递减平均统计降尺度方法建立起了贵州省本地化的单模式数值预报温度客观订正模型，且具有一定参考价值，可进一步改进并尝试业务化运行。

总体上来说，基于类卡尔曼滤波递减平均统计降尺度方法建立起来的订正算法模型，具有较好的订正效果，且具有计算量小，需要资料序列较短的特点，便于业务化。同时，在w参数训练上仍然有很大的提升空间，有望进一步提升订正质量高的站点数量和参考价值，在业务中发挥作用。但仍存在以下几个问题：

①目前对于滑动训练的算法方案设计的过于简单，导致订正效果不好，但是如果设计方案过于复杂，难以回避训练期较长或者需要的历史资料周期较长等问题，在业务化过程中就会伴随计算量大和资料难以保障的问题。下一步的难点在于如何能在较短资料序列和较小计算量的情况下滑动训练出比较好的订正预报。

②基于类卡尔曼滤波递减平均统计降尺度方法建立起来的方案订正效果是明显的，但是具有较好参考价值的站点比例并不高，原因在于w训练方案仍有很多不足之处，下一步可以尝试引进卡尔曼滤波的增益函数对w进行训练。从卡尔曼滤波原理出发，有望进一步改善订正效果，为日常温度预报业务提供参考，建立起更好的贵州省本地化的温度客观订正预报模型。

③目前的客观订正算法只是停留在单模式的计算，订正的效果始终是有限的，待下一步引进卡尔曼滤波增益函数后，可以尝试建立多模式集成的温度预报客观算法订正模型。