基于云模型-LSTM的光伏功率中期预测

张晋华 ，2，黄远为 *，冯 源

（1.华北水利水电大学电力学院，河南 郑州 450045；2.新能源电力系统国家重点实验室（华北电力大学），可再生能源学院，华北电力大学，北京 102206）

0 引言

近年来，全球范围大力发展太阳能、风能等清洁能源。截至2020年底我国光伏发电累计装机达2.53亿千瓦，如何最大程度保证光伏发电能够安全、高效地消纳成为一大难题［1-3］。光伏发电具有随机性、不确定性的特点，精准的功率预测能够指导电网调度部门合理安排，减少光伏电站接入对电网的冲击和弃光现象的发生［4-5］。光伏功率预测按时间尺度可分为超短期预测，短期预测以及中长期预测［6］。当前我国新能源功率预测3 d的时间尺度不能与火电的启停5-7 d的周期相匹配，调度部门不能将新能源纳入开机计划进行有效指导［7］。因此，对光伏功率进行周期为7 d的中期预测具有现实积极意义。

传统的光伏功率预测方法有物理方法和统计方法［8］。物理方法是参照光伏电池的发电原理，利用数值天气预报（Numerical Weather Prediction，NWP），卫星、地面场站实时数据，结合光伏电池安装角度、光伏阵列转换效率等参数，建立物理模型直接计算得到光伏功率数据［9］。物理方法对数据精度要求高，且模型参数多，构建难度大。统计学方法是输入太阳辐照度、光伏功率等历史数据，通过曲线拟合、参数估计等方法，建立输入与输出的映射模型从而实现预测。相比物理方法，统计方法因其模型搭建简单，所需数据容易获取而被广泛应用于光伏功率预测中。常用的统计学方法有：灰色模型［10-11］、人工神经网络［12-13］、支持向量机［14-15］等。然而传统算法面临着泛化能力不足和易陷入局部最优问题，预测精度难以提高［16］。

LSTM神经网络作为一种深度学习算法，能够准确描述此类复杂非线性映射关系，近来不少学者将其应用于光伏［17-18］、风电［19-20］及负荷预测［21］等领域。文献［22］基于多维气象因素间的加权互信息熵从历史日中筛选出预测日的相似日样本，利用LSTM预测模型建立起气象因素与光伏输出功率之间的映射关系，在多种气象条件下进行了预测分析，得到了良好的预测精度。文献［23］在选取周边电站考虑其空间相关性的基础上，利用相关性强的参考光伏序列同目标电站历史光伏数据一起构建LSTM预测日模型，相较于未考虑空间相似性分析的预测模型，精度得到了提升。选择文献［24］引入了Davies-Bouldin指数得到自适应Kmeans算法，利用该算法分别对晴天、多云以及雨天这三类气象条件下的总辐照度、湿度、温度以及光伏功率进行聚类分析，最后将每一类的训练集代入LSTM预测模型，得到预测结果。以上LSTM神经网络在光伏功率预测中的研究集中在短期预测，尚未应用于时间尺度更长的中期预测中。

基于以上分析，本文提出了一种基于云模型-LSTM的光伏功率中期预测方法。方法首先以辐照度为样本建立每日辐照度云模型，通过云变换得到云的数字特征，将数字特征代入云模型的相似度计算模型，选取相似日。最后将相似日数据作为训练集代入LSTM预测模型进行预测，得到光伏功率。

1 基于辐照度云模型的相似日选择

1.1 云模型的概念

云模型是由李德毅院士在上世纪90年代中期提出的用来描述定性概念与其定量表示之间的不确定性转换模型［25］，设U是一个定量的论域，U上对应的定性概念为C，对于该论域的任意元素x，都由一个具备固定倾向的随机数y=μC（x），该随机数称作x对概念C的确定度，x在该论域上的分布称为云模型。云模型用期望、熵、超熵三个数值特征来描述一个概念［26］。

1）期望Ex

Ex是云滴在空间分布中的数学期望，即最能够代表定性概念的点。在辐照度云模型中，期望值代表当日所选时段平均辐照度的大小。

2）熵En

熵值是定性概念的不确定性度量，由概念的随机性、模糊性一同决定。熵值描述了辐照度的随机概率分布情况，熵越大，说明当天辐照度波动越不具备规律性。

3）超熵He

超熵是熵的熵，是熵的不确定性度量。

云模型由正向云变换和逆向云变换实现定性概念与其定量表示之间的不确定性相互转换，它把模糊性与随机性集成到一起，构成定性与定量之间的映射［27］。根据文献［26］提出的方法构建辐照度云模型。

1.1.1 正向云变换

输入：当天辐照度的三个数字特征Ex，En，He；辐照度云滴数n；

输出：n个辐照度云滴xi以及每个云滴的确定度yi，i=1，2…，n。

步骤1：生成以En为期望，He2为方差的一个随机辐照度Eni；

步骤2：生成以Ex为期望，Eni为方差的一个辐照度云滴xi；

步骤3：计算yi=exp（-（xi-Ex）2/（Eni）2），为辐照度xi出现的概率；

步骤4：重复步骤1到3，直至产生n个辐照度云滴为止。

1.1.2 逆向云变换

输入：辐照度x1，x2，…，xn，xi为单点时刻辐照度值，n为辐照度点数量。

输出：辐照度的数字特征（Ex，En，He）。

步骤1：计算当日辐照度的均值，得到期望Ex的估值；

步骤2：将每日辐照度样本x1，x2，…，xn进行随机可重复抽样，共抽取m组样本，每组r个样本点。计算每组样本方差：

步骤3：从样本y12，y22，…ym2中计算En2，He2的估值。

图1、图2分别为正向云发生器和逆向云发生器的示意图。

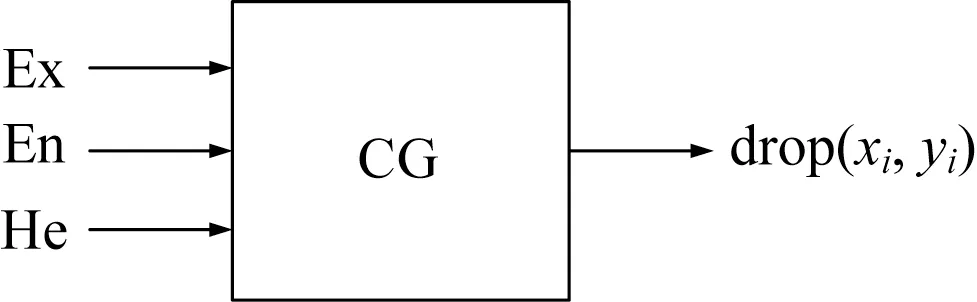
图1 正向云发生器Fig.1 Positive cloud generator

图2 逆向云发生器Fig.2 Reverse cloud generator

1.2 云模型3En规则

模型的3En规则即在［Ex-3En，Ex+3En］区间内分布着99.74%的云滴，由于区间外的云滴数不影响整体特性，故可忽略区间外定量值对定性概念的贡献［28］。

1.3 辐照度云模型的相似性度量

由文献［27］指出的方法计算云C1（Ex1，En1，He1）和云C2（Ex2，En2，He2）的交点f1和f2。

根据交点f1和f2位置关系的不同，在计算辐照度云模型相似度时，可分为以下3类情形。

情形1：交点f1和f2全位于3En区间外。这类情况下的云模型相似度为：

情形2：交点f1和f2有一个位于3En区间内。先求出此时C1与C2的重叠度ol［27］，这种情况下云模型的相似度为：

式（3）中，μ为两条期望曲线交点对应的纵坐标，即确定度值。

情形3：交点f1和f2均位于3En区间内。此时云模型的相似度为：

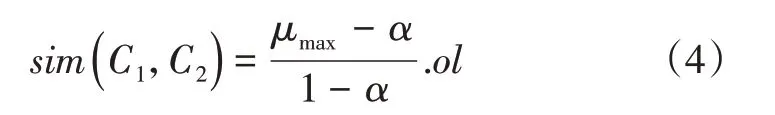
式（4）中，μmax为交点f1和f2对应的两个确定度中，数值更大的一个。

云模型相似性度量具体算法如下：

输入：两个云C1（Ex1，En1，He1）、C2（Ex2，En2，He2）。

输出：云模型相似度值Sim（C1，C2）。

步骤1：先求出两个云的交点f1和f2；

步骤2：计算辐照度云模型的相似度Sim（C1，C2）；

步骤3：重复步骤1、2直至计算完所有天数同预测日辐照度云模型的相似度；

步骤4：对相似度进行排列选取相似度最高的3天作为预测模型的训练样本。

2 LSTM神经网络

LSTM神经网络由Hochreiter与Schmidhuber在1997年提出，旨在改进RNN的缺陷［29］。LSTM神经网络在RNN的基础上引入了细胞状态，并使用输入门、遗忘门、输出门3种门来保持和控制信息，可对较长时序信息选择性地通过和剔除。LSTM改善了传统RNN网络在长时间序列学习过程中易出现的梯度消失和梯度爆炸现象［30］。图3为LSTM神经网络的结构图。

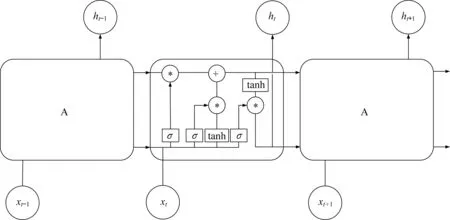
图3 LSTM神经网络结构图Fig.3 Structure of LSTM neural network

LSTM模块当前输入时刻为t，存储单元由以下构成。

输入门：记忆一部分遗忘门输出的信息和当前的信息；

遗忘门：读取上一层输出ht-1以及当前输出xt，输出ft并将其赋值到当前的细胞状态Ct-1中；

更新门：将过去的细胞状态Ct-1和当前的细胞状态C˜合并，输出得到当前的信息Ct；

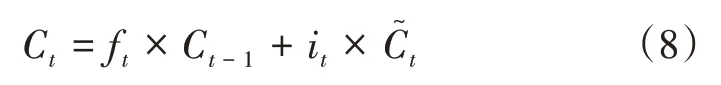
输出门：选择部分细胞状态C˜，输出。

3 预测步骤

3.1 辐照度云模型的相似性度量

将每天原始辐照度样本进行随机可重复抽样，抽取m组样本，且每组抽r个样本点，抽样结果代表当天辐照度的情况。将这m组辐照度样本代入逆向云模型进行计算，得到m组（Ex，En，He）数字特征，最后对m组数字特征取平均值作为当日辐照度逆向云计算结果。经多次验证，m和r分别设置为20和25进行随机抽样较为合理。

3.2 LSTM预测模型设置与预测

3.2.1 输入层与输出层节点数目

选取辐照度、温度和湿度数据作为LSTM预测模型的输入，光伏功率作为神经网络的输出。在构建LSTM光伏功率预测模型时，将历史日的以上气象因素与光伏输出功率一一对应，作为训练集。将预测日的辐照度、温度、湿度作为测试集输入，得到预测日的光伏输出功率。由此确定光伏功率中期预测模型的输入层和输出层节点个数分别为693和231。

3.2.2 隐含层节点选择

隐含层单元数目为用于记忆和储存过去状态的节点个数。若设定数目过少，则LSTM网络无法全面学习，误差较大。若隐含层单元数目过多，则LSTM网络学习速度慢，且易发生过拟合现象。根据经验公式取得估值，反复多次实验，确定LSTM隐含层节点j。经验公式如下：

式（11）中：j为隐含层个数；k为输入层个数；l为输出层个数；a为1到10中任一常数。

由表1可以看出，当隐含层数目为30时模型的均方根误差最小，由此将模型的隐含层节点数设置为30。

表1 隐含层节点个数确定Table 1 Determination of number of hidden layer nodes

3.2.3 数据标准化与标准化还原

由于激活函数的特性，使得神经网络对区间［-1，1］内的数据敏感。若输入数据在此区间，则会大大提升训练速度，获得较好的拟合曲线，避免训练发散。因此，首先将训练数据标准化，使其具有零均值和单位方差。最后将输出的数据进行标准化还原，得到预测的光伏输出功率。

3.3 评价指标

本文衡量预测效果的指标采用平均绝对误差百分数（MAPE）以及均方根误差（RMSE）。计算公式如下：

式（12）、式（13）中，Pi为第i个预测功率数据的真实值；Pi'预测值；Pcap为该光伏电站的装机容量；n是样本个数。

4 算例分析

采用国内某光伏电站现场实测数据进行预测。该电站装机容量为50 MW，实测数据包含辐照度、湿度、温度、风速、风向及光伏发电功率。为了验证所提预测方法的有效性，考虑季节差异，选取每日时段为9：00到17：00，采样间隔15 min，一天采样33个点。本文考虑了电站春夏秋冬4个季节，在实验中引入长短期记忆网络（LSTM）、灰色模型（GM）、支持向量机（SVM）等预测模型进行光伏功率预测，最后与本文提出的云模型-LSTM模型预测结果对比，如图4所示。

由图4（a）可以看出，除了前两日的功率曲线有些许波动外，七日内整体功率曲线的随机波动频率较低，且波动幅度较小。各模型的预测曲线与真实值拟合程度都比较高。相比于图4（a）冬季，图4的（b）、（c）、（d）春夏秋3个季节的功率曲线波动频率更高，波动幅度也相对更大。预测效果不及冬季7日预测，原因是电站所处地区冬季空气中水汽含量低，云层少。云层作为主要的天气突变因素，直接影响地表辐照度水平。当光伏功率曲线波动频率高，波动幅度大时各模型的预测精度也随之下降。但对比其他模型的预测曲线可以看出，本文所提云模型-LSTM的预测曲线更接近真实值，反映了云模型-LSTM具有较强的学习能力。

图4 预测结果Fig.4 Forecast

表2为在春夏秋冬四个季节的不同预测模型进行光伏功率预测的误差对比。由表2可以看出，在冬季时各模型的预测效果均比其他季节的要好，且本文提出的云模型-LSTM预测光伏功率中期模型预测误差更小。上述结果表明，云模型-LSTM具有更好的预测精度，在不同季节均可以更好地对光伏功率进行预测。相比于LSTM预测模型，云模型-LSTM在冬春夏秋四个季节下的MAPE分别降低了40.10%、8.40%、5.75%和19.56%，RMSE分别降低了46.43%、2.20%、2.24%以及3.42%。这表明结合了云模型的LSTM模型在预测精度上有进一步的提升。特别地，冬季光伏功率预误差明显降低，这反应在冬季季节气候时云模型能够筛选出与待预测日高度一致的历史日，而对于其他季节，在天气相对复杂时，云模型的这一表现有所降低；LSTM预测模型相较于SVM和GM，在冬季MAPE分别降低了10.66%、9.74%，RMSE分别降低了9.98%、9.37%；在春季MAPE分别降低了10.08%、11.50%，RMSE分别降低了3.93%、4.50%；在夏季MAPE分别降低了3.74%、4.16%，RMSE分别降低了1.73%、16.33%、；在秋季MAPE分别降低了7.13%、18.89%，RMSE分别降低了5.25%、2.54%。这也表明了相对于传统统计学算法，LSTM具备泛化能力强，预测精度高的特点。

表2 预测误差统计表Table 2 Statistical table of forecast error

5 结语

本文提出了一种基于辐照度云模型与LSTM的光伏功率中期预测方法，首先提取每日辐照度形成训练集，然后利用云模型的相似性度量计算选取相似日，最后利用LSTM神经网络对光伏功率进行预测。为了验证预测的性能，本文以国内某光伏电站实测数据为研究对象与传统LSTM、SVM以及GM模型进行对比实验，结果表明，本模型在不同季节、不同气象条件下均能够提升光伏功率中期预测的精度，具有一定的研究价值和应用前景。

本模型的主要不足之处在于对复杂气象条件下的预测精度未有明显提升。此外，当前建立的云模型在进行相似日选取时仅考虑了辐照度，在未来的研究中可以考虑纳入更多诸如温度、湿度等其它影响因素，筛选出与待预测日气象条件更加相近的历史日。