NACA埋入式进气口气动特性试验设计优化

朱德轩，杨 旸，余志健，李志鹏，张 冬

(1.中国商飞上海飞机设计研究院，上海 201210；2.中国科学院工程热物理研究所南京未来能源系统研究院，南京 210000；3.中国科学院工程热物理研究所先进燃气轮机实验室，北京 100190)

民航飞机飞行时燃油箱需要与外界大气连通以保证油箱结构的安全。同时，飞机惰化系统和环控系统也需引入外部冷却空气以满足系统运行需求。对于民航飞机来说，目前主要有两种进气口设计，分别为戽斗式进气口和埋入式进气口。与戽斗式进气口相比，埋入式进气口没有外部突出物，降低了对飞机气动阻力的影响。同时无需支撑加固结构，重量较轻。埋入式进气口主要为(美国)国家航空咨询委员会(National Advisory Committee for Aeronautics，NACA)埋入式进气口，该种进气口已在波音、空客及中国商飞等若干机型上得到广泛应用。

NACA埋入式进气口，通过侧边产生一对轴向涡，将壁面气流卷吸入进气通道[1]。但由于进气口通常位于较厚的边界层内，吸入的为边界层中低能气流，导致进气流量减少及出口气流不均匀度高[2]。同时由于飞机在高马赫数(Ma)下飞行，在NACA进气口前部喉道位置容易产生激波，增加气动阻力，恶化气动性能。

因而，需对NACA进气口进行气动优化设计。徐尚成等[3]将一体化设计方法应用于进气道设计, 采用特征线法设计了5种不同型面的前体。乔文友等[4]提出一种基于前体激波形状的一体化设计方法，以使进气道捕获截面和唇口型线与飞行器前体激波匹配。李怡庆等[5]对圆锥流场在不同攻角条件下的气动特征进行分析, 以流线追踪技术为基础，发展了一种曲锥前体/三维内转进气道一体化设计方法, 获得了3个几何参数对一体化方案外形和性能的影响规律。为设计低噪声进气道，邱昇[6]提出了一套基于声学伴随方法和梯度增强代理模型的高效优化设计框架。李静等[7]提出了一种三维进气道沿程结冰参数分析方法，并考察了进气道参数对结冰的影响。在实际进气道工程设计上，上海飞机设计研究院薛勇等[8]基于试验数据获得的进气口总压恢复系数和截面捕获流量比关系，确定飞机极热天巡航状态设计工况点，而后根据NACA推荐尺寸比，确定最终尺寸。王赟等[9]提出在满流量基础上以燃油代偿损失为综合评价指标进行设计。

国外Soltani等[2]对超音速混合压缩进气道进行了实验研究。以总压恢复系数、质量流率和流畸变为进气性能指标。结果表明，应用边界层抽吸上游的摄入量喉咙可以大大提高进气性能的设计和非设计工况条件而不影响进气质量流量。Javed等[10]采用计算流体力学方法计算了超燃冲压发动机引擎进气系统的质量捕获率。

现有进气道设计研究主要针对超声速或发动机进气道，考虑减小发动机前进气畸变。设计中兼顾进气道进气噪声及结冰等特性。对于民用客机公用系统进气道研究较少。各结构参数对客机公用系统进气道性能参数影响特性研究较少。工程设计上直接采用基于边界层的理论公式计算进气口参数，各关键几何尺寸采用NACA早期推荐值，各几何参数的具体影响机制和作用机理无法解析。且对于非平行面组成的进气口，斜坡底部的流动发散，且外流不平行于斜壁，有涡形成，理论模型精度不足。

为解决上述问题，现采用计算流体力学(computational fluid dynamics,CFD)方法建立民机公用系统NACA埋入式进气口数值模型，对其气动特性进行分析，并以阻力、总压恢复系数、出口质量流量和出口马赫数为性能指标进行几何参数优化设计。首先，理论分析确定几个关键的进气口几何控制参数，通过试验设计(design of experiments，DoE)方法进行参数优化，通过统计回归找出最优的几何参数组合结构。并对试验设计结果进行方差分析(analysis of variance, ANOVA)[11]，分析出各控制参数各自及相互影响规律。同时基于CFD计算结果详细研究各几何控制参数对进气口速度、压力分布、涡强度及流线等气动特性影响机理，最终获得具有最佳气动特性的进气口几何结构参数。

1 数值方法

1.1 几何及边界条件

所用的NACA进气道几何结构如图1(a)所示，由进气口、斜坡、转角及尾通道组成。基准工况：出口尺寸68 mm×24 mm，斜坡高30 mm，转角外半径30 mm，内半径10 mm, 出口高度232 mm。整体计算域如图1(b)所示，坐标原点位于进气口前缘尖角位置，计算域进口距离前缘尖角1 m，通气口后1 m结束，侧面各留0.5 m长，向下扩展0.7 m。气流经过NACA通气口后拐角转90°向上连接火焰抑制器，计算采用直通口，并预留一定长度直通道。进气口附近表面为壁面，主流计算域四周及底面采用压力远场边界，进气口出口为压力出口边界条件。主流参数如表1所示。

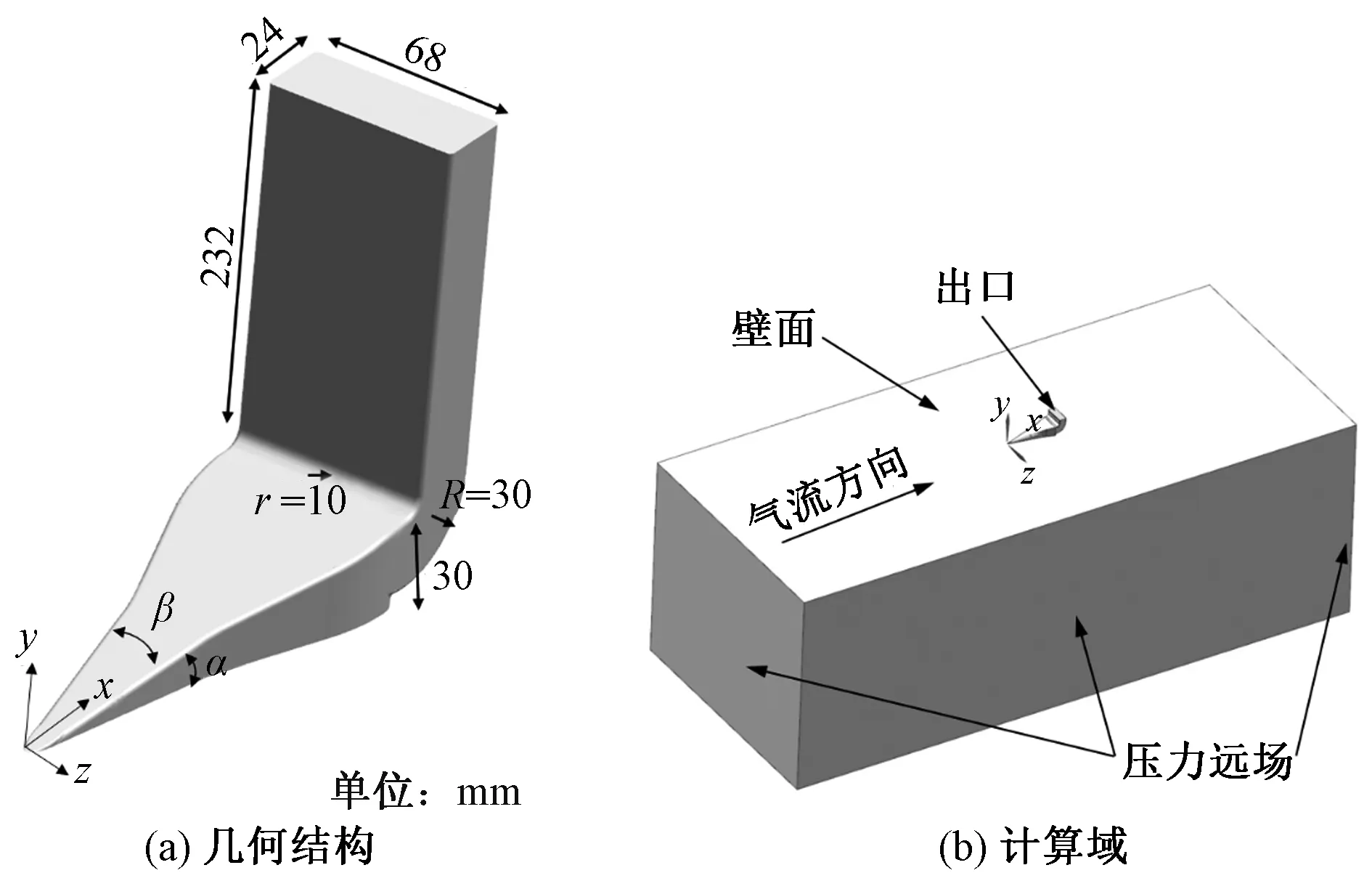
α为斜坡角度；β为斜坡锥角；r为内折转半径；R为折转角半径

表1 主流参数

1.2 网格与网格无关性

主流壁面和NACA进气口壁面采用3层棱柱层网格，网格第一层高度分别为0.025 mm和0.02 mm，保证无量纲壁面距离y+≈1[12]，由于选用k-omega SST(shear stress transfer)湍流模型，仅研究型面的影响，选择巡航设计点作为单一边界条件，因此对于不同计算工况采用同一套网格分辨率划分。对整个计算域进行分区划分混合网格。对于NACA进气口及进口向下10 mm单独分区采用空间分辨率1.25 mm的结构化多面体网格；进气口四周一定范围单独分区采用分辨率4 mm的结构化多面体网格；其他区域采用分辨率15 mm结构化多面体网格。结构化网格以及边界层网格的交界面处，采用了非结构网格进行填充。由于NACA通气口为边界层进气，非结构填充将极大减小求解过程的数值耗散问题。整体网格划分和局部网格细节如图2所示。

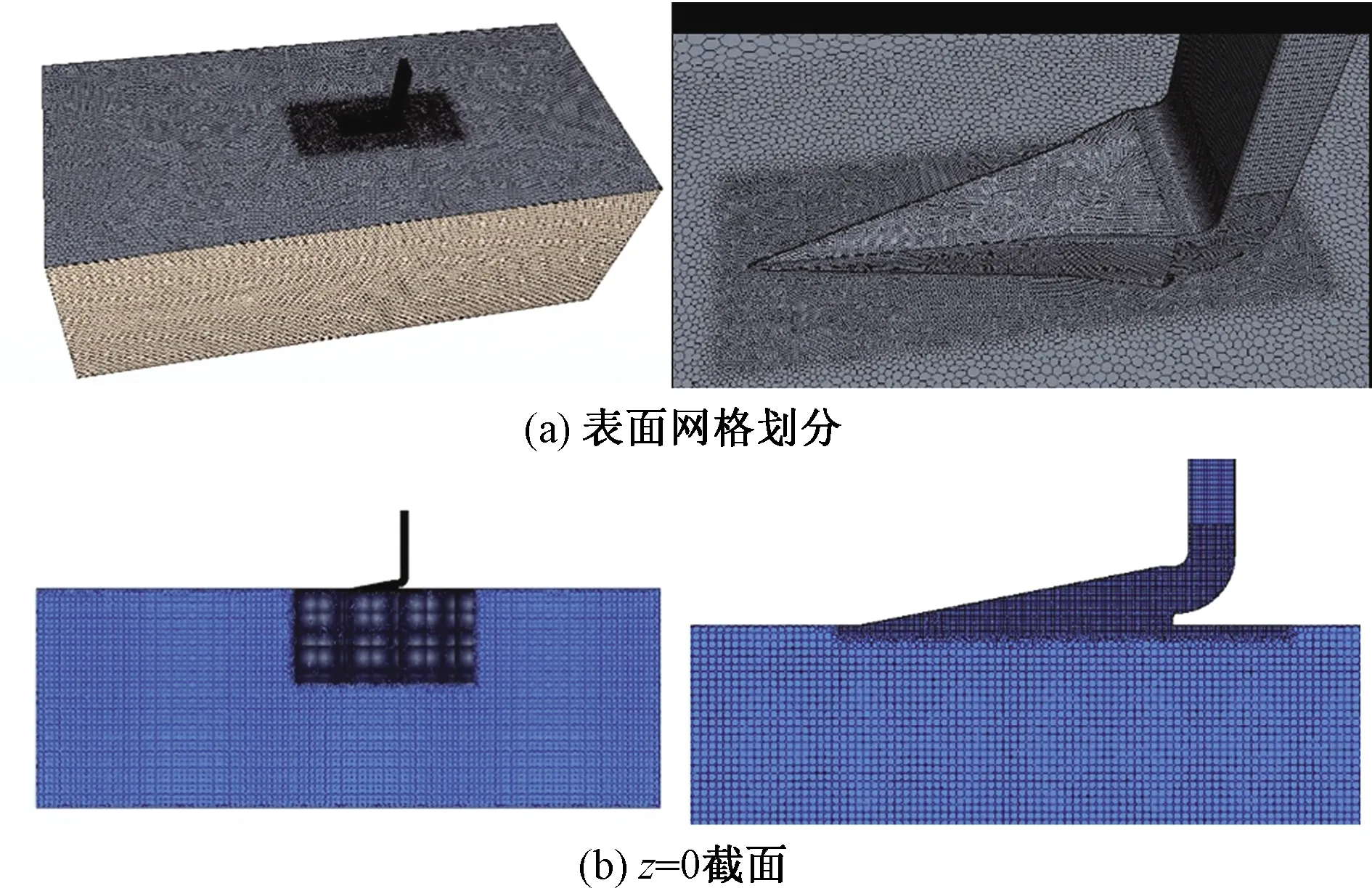
图2 整体和局部网格划分

对网格进行无关性验证。在不改变壁面棱柱层网格高度的情况下，对划分的3个区域分别进行加密，使得主流、靠近通气口区域及通气口内部包含折转部分增加和减少20%的节点，分别划分出110万、197万和297万三套网格。

图3、图4和图5为不同网格数量下进气口轴向涡发展截面(x=0.08 m)x方向、y方向及z方向速度分布。x=0.08 m处，边界层开始有向进气口内部发展趋势，两个轴向涡已经发展完成。将197万的网格进一步加密到297万，并不能明显改变速度分量沿展向的数值，但加密后计算的速度分布还是有轻微的变化，由于297网格不算太多，因此后续将采用297万网格策略。

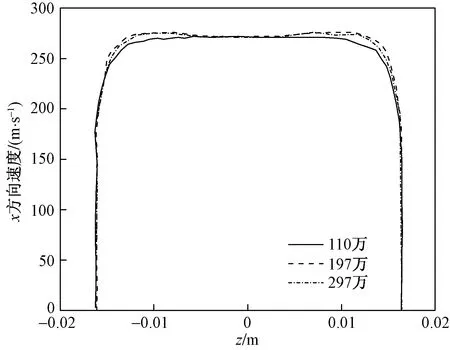
图3 不同网格数量下截面(x=0.08 m)x方向速度分布对比

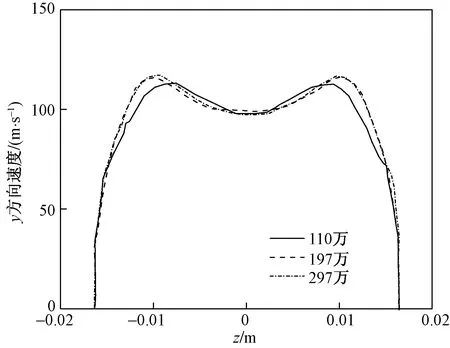
图4 不同网格数量下截面(x=0.08 m)y方向速度分布对比

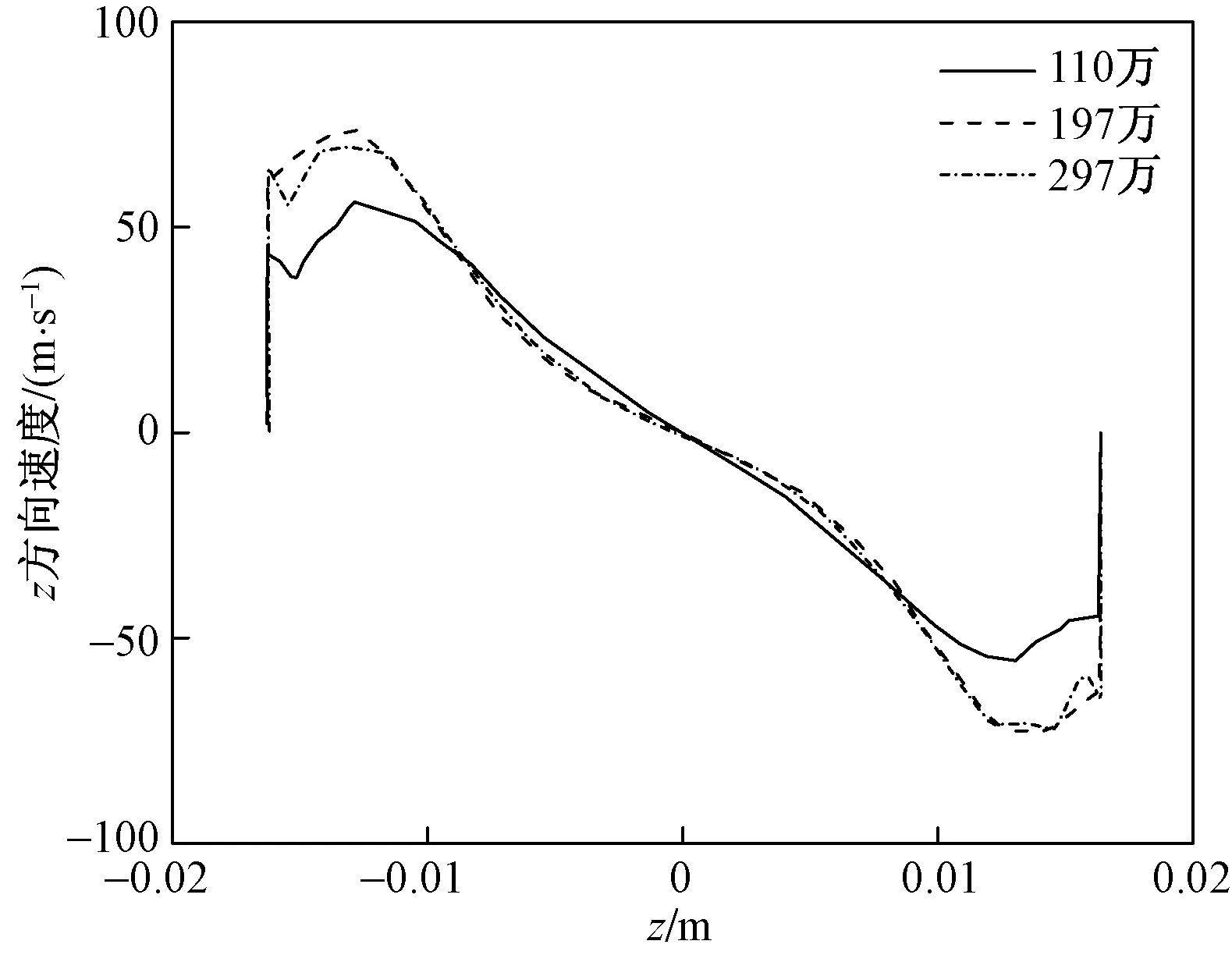
图5 不同网格数量下截面(x=0.08 m)z方向速度分布对比

1.3 数值方法

稳态RANS(Reynolds-averaged Navier-Stokes)计算采用k-omega SST湍流模型，并采用密度基求解器求解。密度采用理想气体定律，比热容采用分段多项式，动力黏度采用Sutherland模型。湍流动能和湍流耗散率采用二阶迎风格式离散，操作压力选为零值。壁面均为绝热条件。

1.4 DoE设计

根据三角翼[13]与四面涡发生器[14]理论，进口坡度对轴向涡产生有重要作用，而对于NACA进气口需加强轴向涡还是减弱轴向涡，文献暂未给出结论。现有NACA通气口侧边根据文献[15]设计，而NACA原始文献中，该形状是从三角形出发，依据减少进口展向角度修型获得。对于型面设计是否影响进气口气动性能未有详细分析。

如图6所示，NACA进气口斜坡形状可以简化成两个三角形，并用光滑曲线进行连接[16]。根据型面曲线结果，β可保持不变以减少参数个数，且民航飞机巡航马赫数低于1。

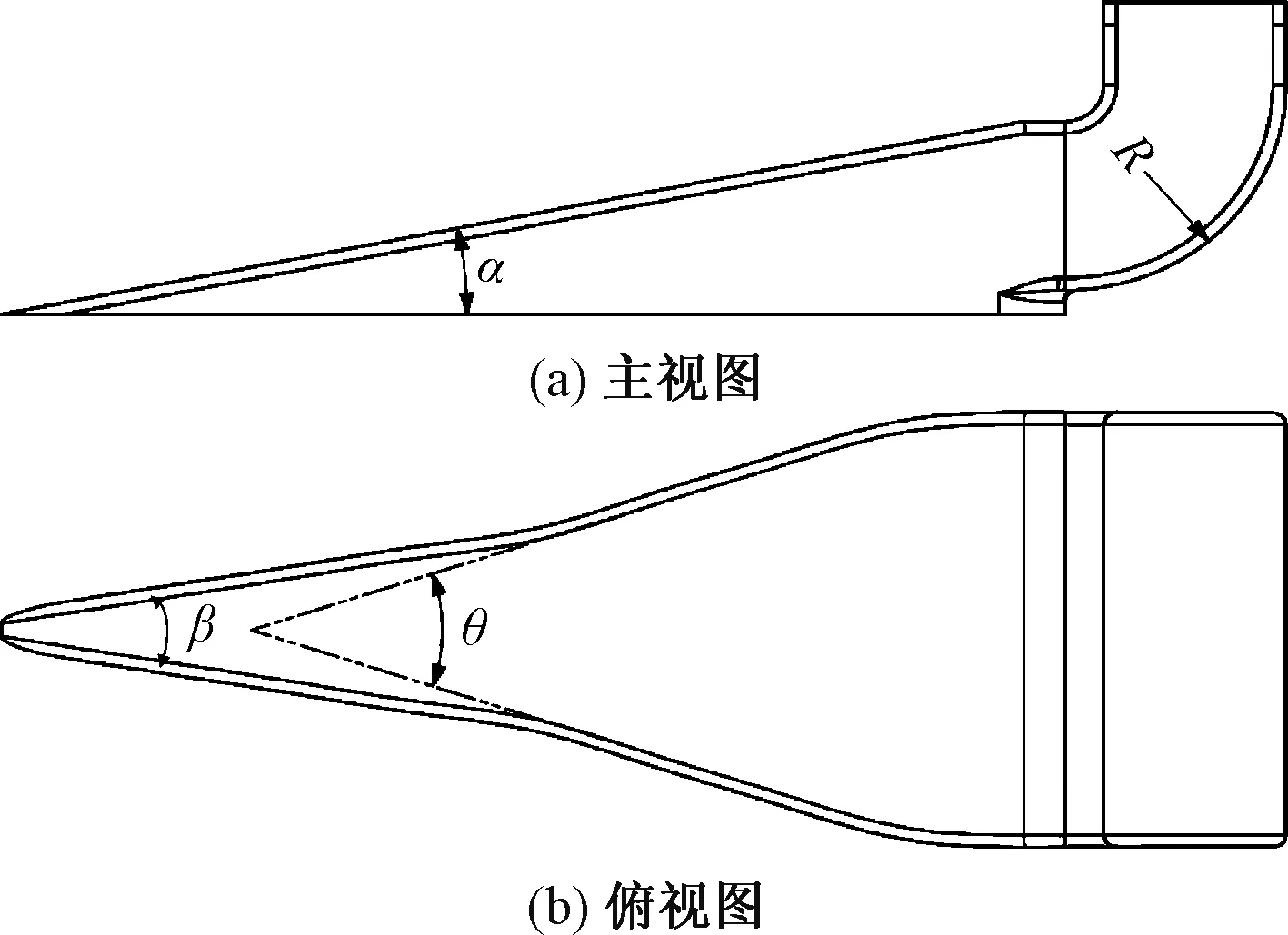
图6 关键几何控制参数

因此主要研究进气口3个关键几何参数，如图6所示分别为α、θ和折转半径R。在主流体域及网格策略不变的情况下，固定折转角出口几何尺寸及其下游几何域进行试验设计。对3个因素进行三水平设计，确定3个因素对性能的影响是否有非线性；再从中筛选出8个算例，对三因素-两水平结果进行方差分析，获得主要影响参数。三因素-三水平取值分析如下。

(1)α。该角度为斜坡角度。在保证折转角不变的情况下，增大该角引起进气口整体缩短。根据三角翼以及四面体涡发生器理论，该角度直接影响轴向涡的形态。主流进气有3°的攻角，而一般平板边界层分离扩散角为11°，因此选取11°、13°、和15°共3个几何变量水平，相应的，主流对斜坡的气动攻角为8°、10°和12°。

(2)θ。该角度为斜坡扩张角，决定斜坡型面拐点位置。θ小则拐点靠近前缘。在NACA报告中没有对此的描述，而是用光滑样条曲线连接了出口与前部三角形。为了量化该型面，采用θ来控制拐点位置，取值范围为36°、40°和44°。

(3)折转角半径R。在保证出口位置一定时，该弧度会影响进气口的阻力以及转向时因面积变化导致的流道内马赫数变化。R的取值为32、40和44 mm。

三因素-三水平的试验设计表如表2所示。

表2 水平试验设计表

1.5 性能参数指标

选取如下4个性能参数指标作为试验设计的因变量。

(1)阻力D。该阻力为作用在NACA进气口斜坡、斜坡侧面以及所有转角面的总摩擦力与压力之和，采用绝对值。

(2)总压恢复系数。定义[15]为

(1)

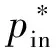
(3)进入进气口的质量流量m，为斜坡出口拐角前截面数据。

(4)斜坡出口拐角前截面平均马赫数。

2 结果与分析

2.1 基准工况

图7为基准工况下进气口表面极限流线和静压分布图。可以看出，在1/2轴向位置的侧面上有低压区，而靠近进气口折转角位置处静压恢复。

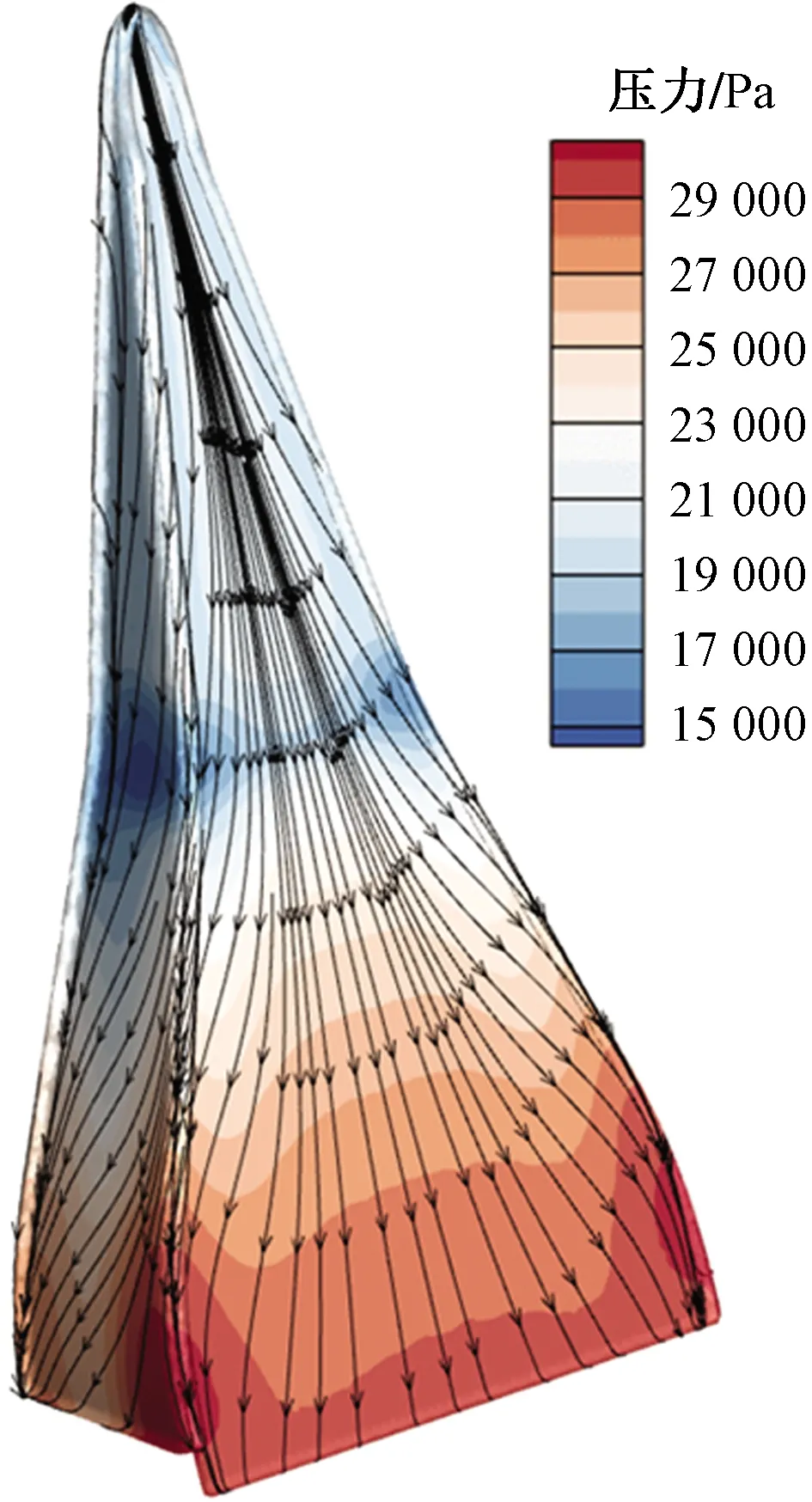
图7 基准工况进气口表面极限流线和静压分布图

表面极限流线表明斜坡底部沿流向流线呈现分散趋势，因此在底部无分离。在侧面靠近通气口底部的侧边，通气口底部流线在此聚集；在侧面靠近主流的一面，侧面流线在此聚集，因此可以推断，主流在侧边卷起轴向涡，并向下游发展。但是这个轴向涡并不贴靠在斜坡底面，否则斜坡底部将会有流线汇聚的现象。

为更形象地分析轴向涡，选取涡量为1.03×108s-1的等值面并用静压染色进行分析，如图8所示。轴向涡从NACA进气口前缘形成，并且始终靠近斜坡侧面与主流相交的侧边，而不靠近斜坡的底部，因此推测侧边的主流与进气口内部压差，以及侧边带来的速度间断面是产生轴向涡的关键，如果希望增强轴向涡，就需要增大压差与间断面，即增大斜坡角并尽量减少侧边的倒角。侧边倒角受制造工艺影响，而斜坡角α是可以设计的。观察两支轴向涡，发现在靠近进气口处静压较低，而在斜坡侧边拐点处，涡管上静压陡升。在侧边形成的轴向涡继续向下游发展，通过90°转角延伸至出口，而且越向下游，两支涡管越有相互靠拢的趋势。在转角附近，速度方向发生变化，该处可被Q涡识别方法捕获，并具有较低静压。

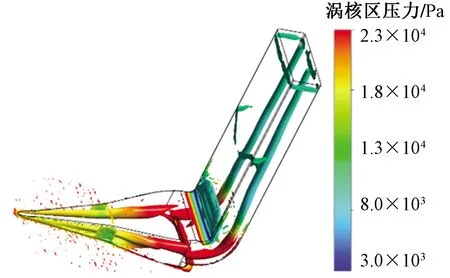
图8 涡核区静压染色图

2.2 DoE结果

DoE 27个算例求解的性能参数如表3所示。可以看出，在斜坡角α为15°的所有组合中，进气口出口马赫数均超过1，而在α为11°的所有组合中，出口马赫数均小于1，当α为13°时，则两种情况均有。当马赫数超过1时，跨过激波面总压损失增大，速度降低，静压升高。单就气动损失而言，是不利的，然而这也是一种短距离内快速降低流入进气口速度的方法。以表3中第2(α=15°)与第27(α=11°)工况为例，在其他参数不变时，尽管高α角(第2个工况)总压恢复系数较低α角的工况缩小了11.12%，阻力降低了9.62%，但低α角流入通气口的气体流量增加了14.57%。

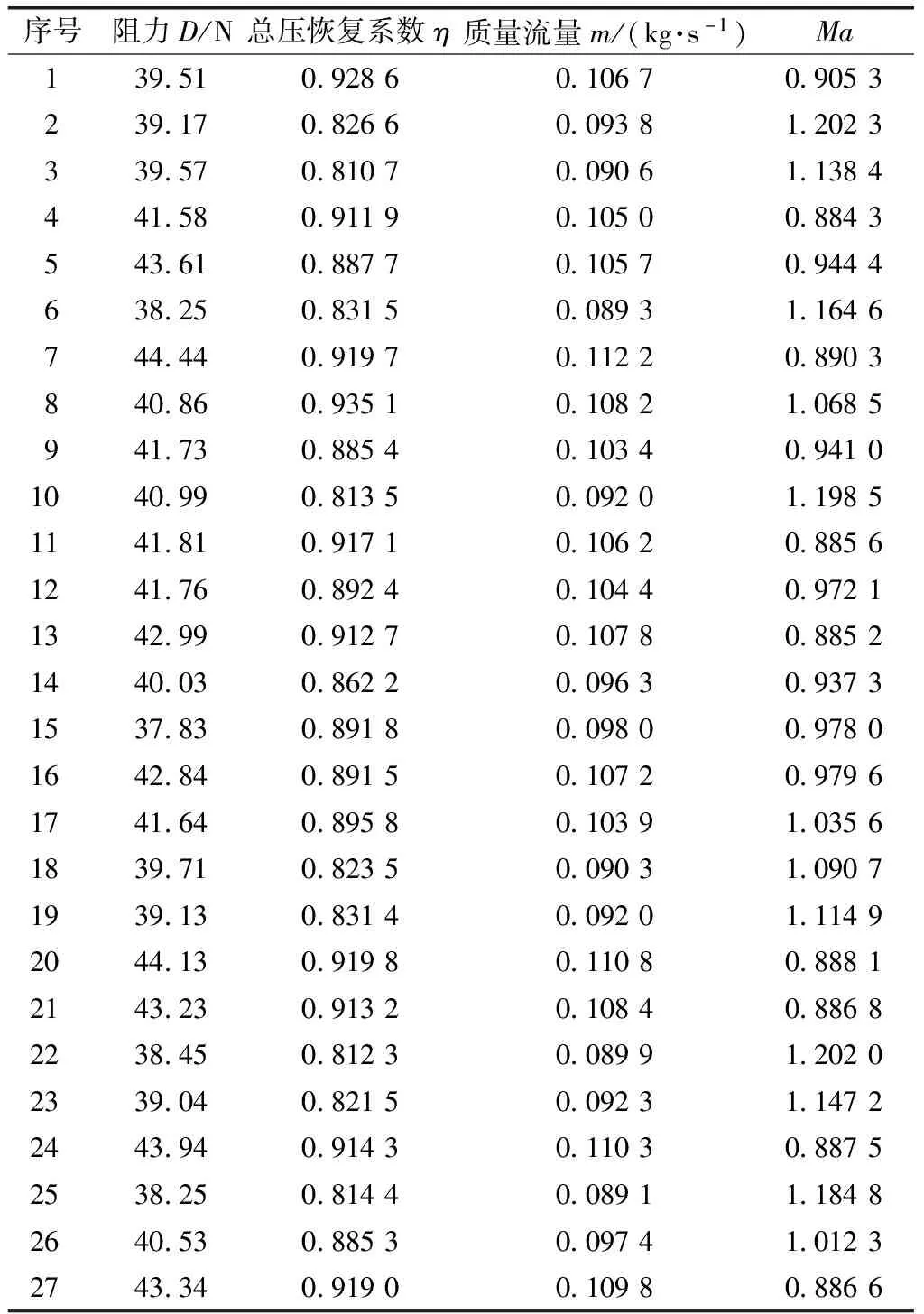
表3 DoE算例计算结果

对表3数据进行三因素-三水平的方差分析，各因素对各性能参数的主效应和交互效应如图9和图10所示。由图9可以看出，θ对阻力有非线性的影响，由于整体影响偏小，且上下限相对平均值小于2%，该非线性影响基本可忽略。α对4个因变量影响较其他两个参数影响大，随着α增大，除了出口截面马赫数外，其他参数值均减小。因此减小α对进气口气动性能提升有利。θ对4种因变量的影响在3个几何参数中最小。除了阻力特性外，其他参数均随θ增大而减小。出口转折半径R对阻力和流量影响大，且均随着折转半径R增大而减小。

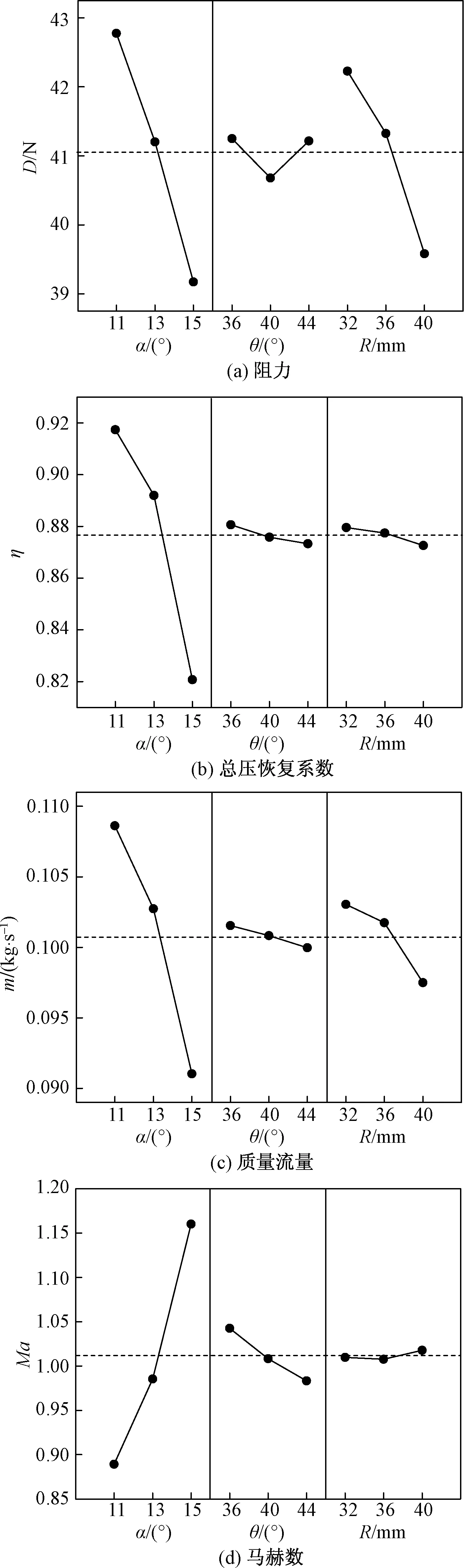
图9 各因素对性能参数主效应影响

从图10交互效应可以看出，阻力和质量流量上α和θ与折转半径R相互影响效应强；总压恢复系数上，各因素之间相互影响弱；出口马赫数上，α和θ之间有相互影响。由主效应分析可知，α越小，总压恢复系数和流量越大，进气口性能越好；而后根据交互效应，在α一定时较小的折转半径和θ对这两个参数有利。表3中工况7和工况27为两个极端参数工况，可见工况27性能较佳。

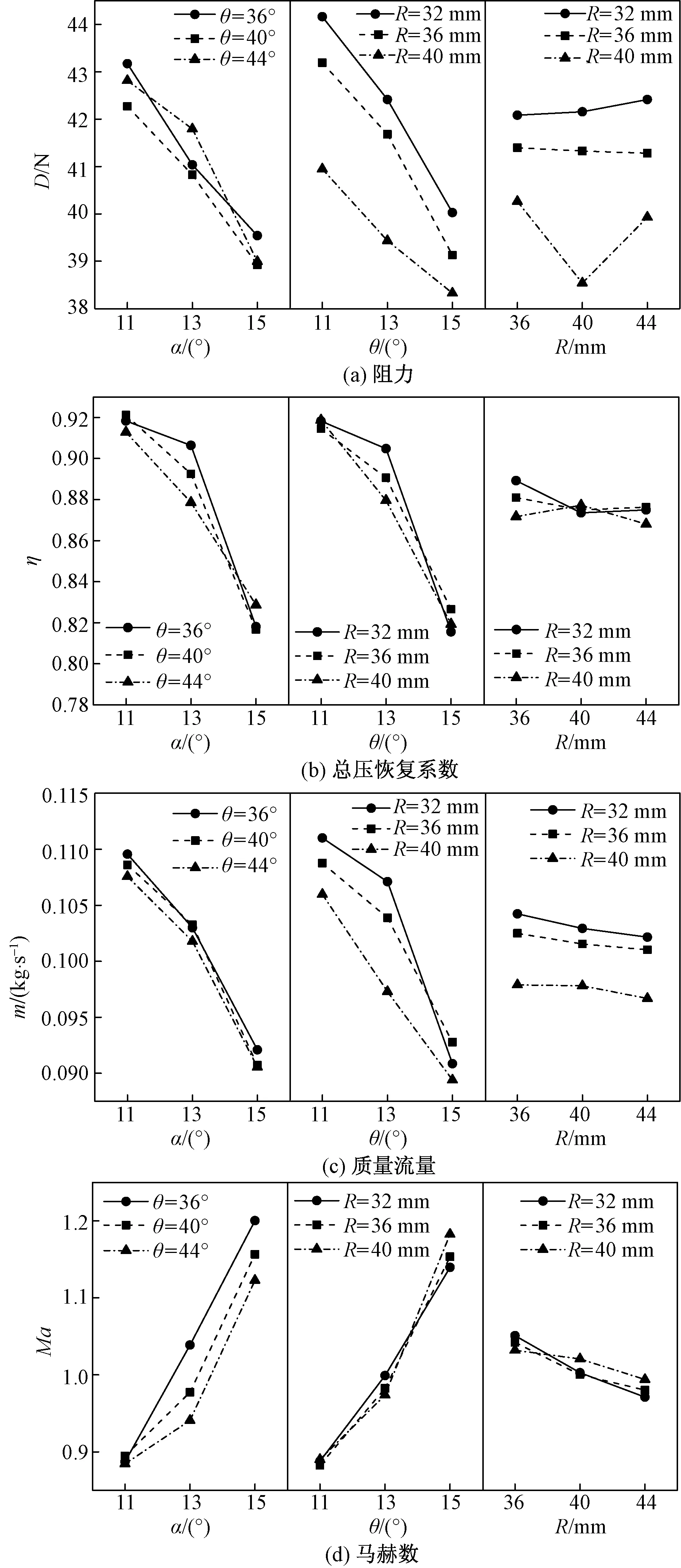
图10 各因素对性能参数交互效应影响

2.3 工况2 和工况27结果对比

由图9可知，α对进气口气动特性影响大，且较小α、θ和折转半径R性能较佳，并进一步比较工况2和工况27性能指标，可得α=11°、θ=11°和折转半径R=36 mm的工况27进气口综合性能最好。因而基于工况27(α=11°)和工况2(α=15°)，其他两参数保持一致，进一步分析α角的影响机制。

图11为进气口涡核区马赫数分布，α越小，进口越大，进气口前缘气流挤压效果越弱，前缘位置马赫数越小。

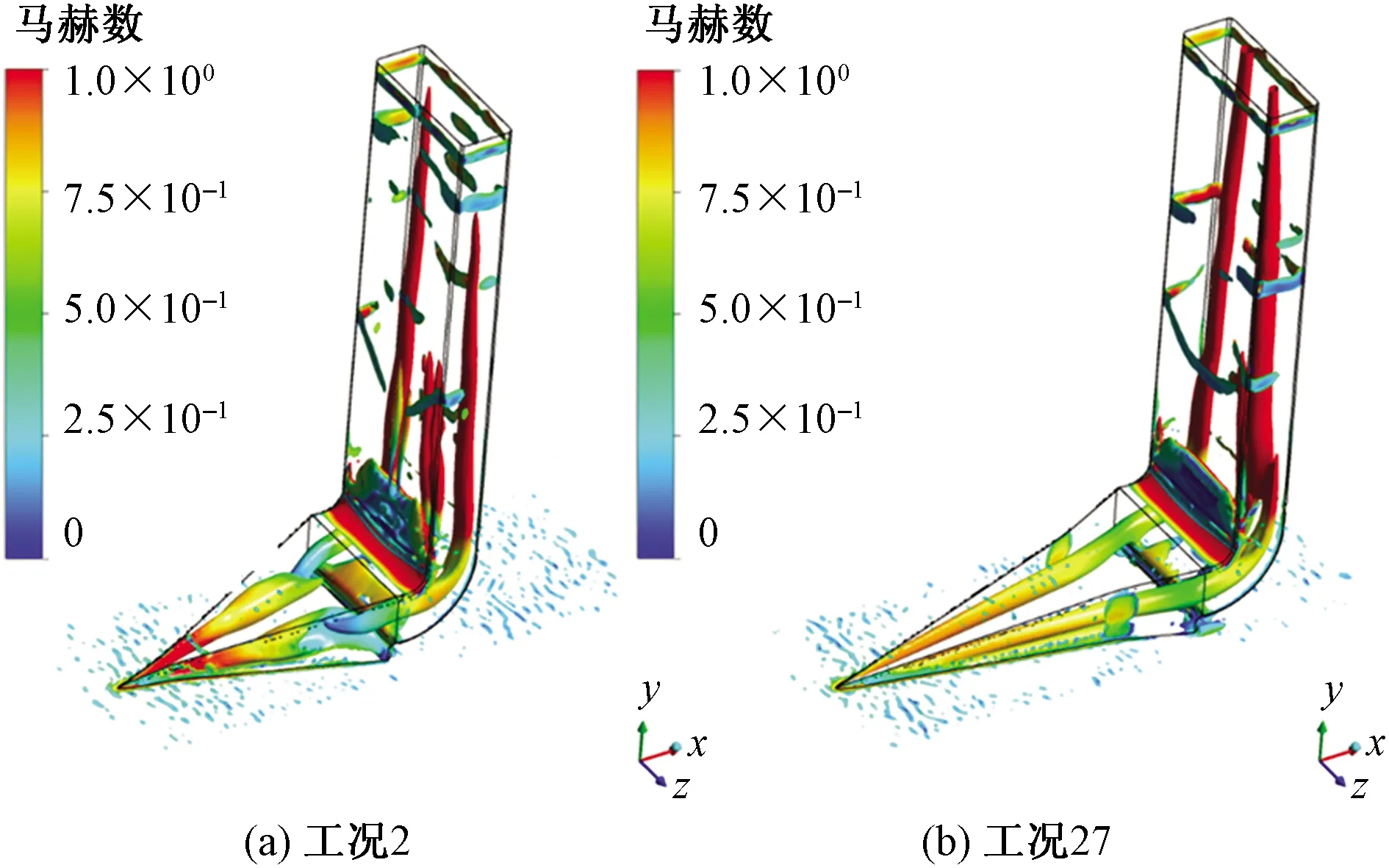
图11 涡核区马赫数分布

图12为涡核区静压分布，α越小，进气口前缘静压越大，对减弱压损有力，斜坡处涡管越长，越有利于卷吸气流，同时涡管向折转通道下游延伸越长，有利于加强下游气流掺混，进而利于出口气流均匀度提升。

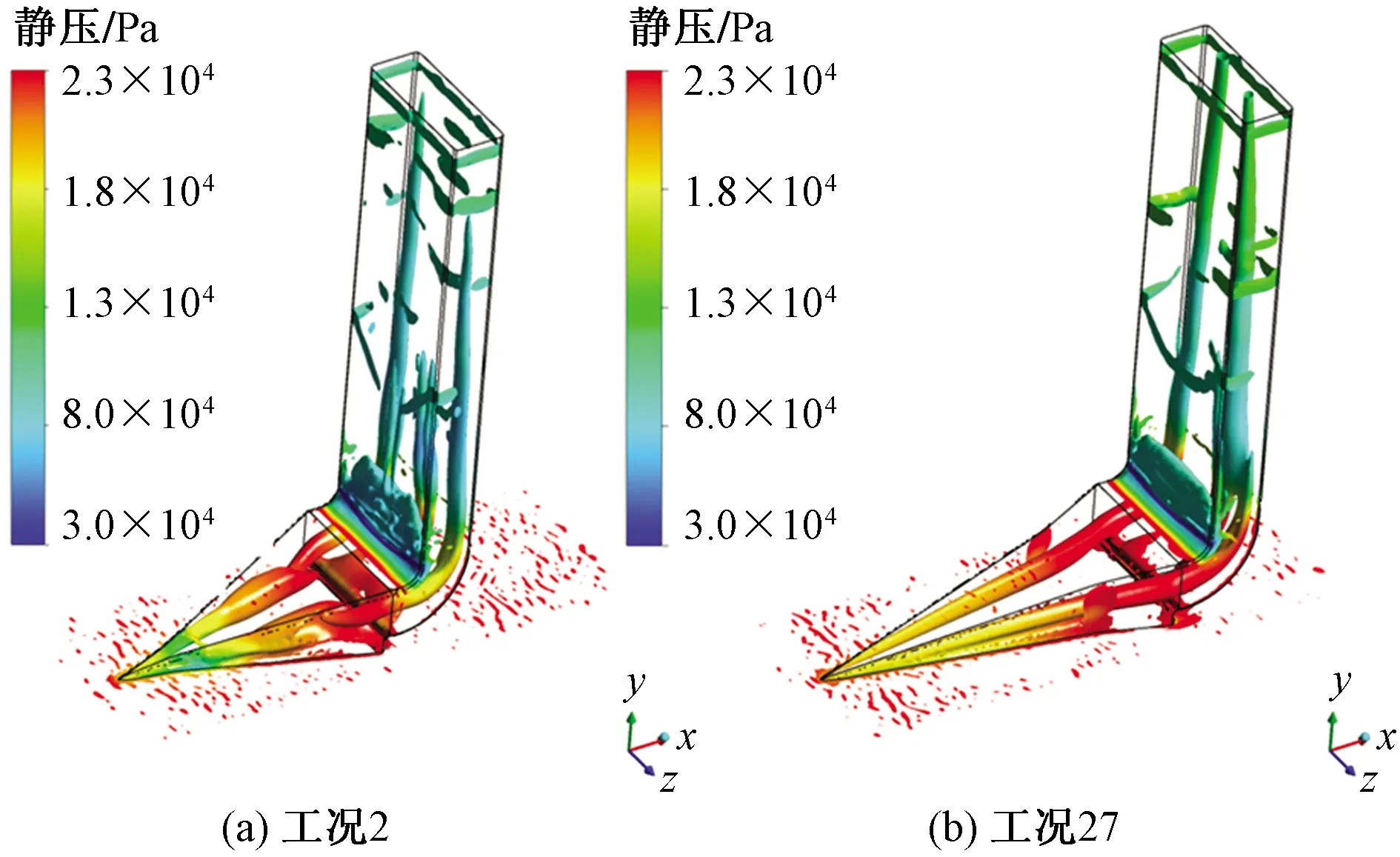
图12 涡核区静压分布

图13为斜坡各截面马赫数分布，可以看出α越小，截面马赫数分布越均匀，且数值越小。图14 为流入进气口流线及斜坡各截面速度分布云图，可以看出α越小，相同位置截面速度分布越均匀。更加均匀的速度分布有利于减小出口畸变，提升进气口进气质量。从流线上看，α越小，壁面分离效果越弱，有利于减弱压损和增加出口气流均匀性。

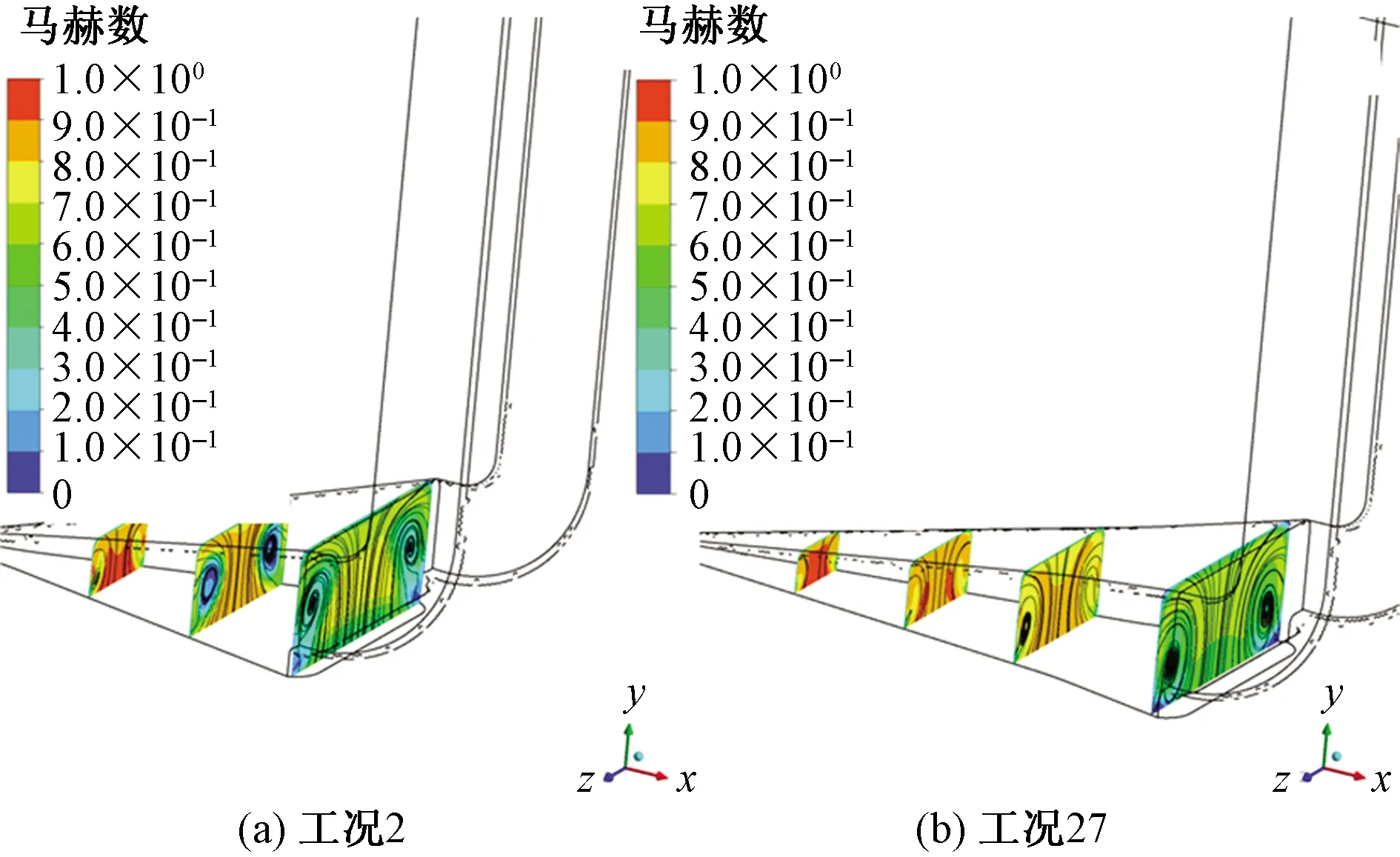
图13 斜坡各截面马赫数分布

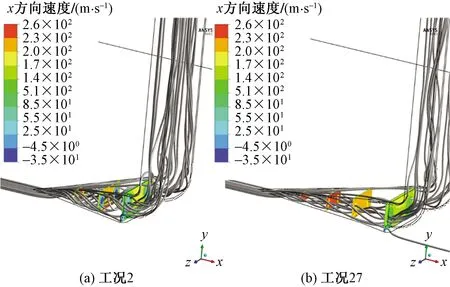
图14 流入进气口流线及斜坡各截面速度分布

3 结论

(1)进气口轴向侧面上有低压区，在斜坡侧边靠近主流处有一对轴向涡，且越向下游，两支涡管越靠拢。

(2)α对4个性能参数影响大，α增大，除出口截面平均马赫数外，其他参数值均减小。θ对性能参数影响小。出口折转半径R对平均阻力和平均流量影响大，且均随着R增大而减小。

(3)交互效应可得，阻力和质量流量上，α和θ与折转半径R相互影响效应强。α越小，总压恢复系数和流量越大。而后根据交互效应，可确定较小的折转半径R和θ性能指标越好。

(4)α越小，前缘位置马赫数越小，静压越大，同时涡管向下游延伸越长，同截面马赫数和速度分布越均匀，壁面分离越弱，有利于减小压损，增加卷吸气流，减小出口畸变，提升进气质量。

综上分析，较小α、θ和折转半径R的性能较佳，并进一步比较工况2和工况27性能指标，可得α=11°、θ=36°和折转半径R=36 mm的工况27进气口综合性能最好。