分散式双馈风电机组接入配电网的不对称短路电流实用计算
付鹏武,杨 波,段振锋,杨东文,邹学谦,贺 智,王登梅,闻宇豪,周念成*
(1.国网湖南省电力公司娄底供电公司,娄底 417000;2.重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
风能作为重要的可再生能源之一,因其清洁环保、储量丰富、分布广泛等优点受到广泛关注[1],随着中国风电发展重心逐渐向负荷密集的中部和东南部地区转移,原本集中式的开发模式不适用于这些地区密集的城镇、人口分布等条件,分布式电源因具有多方面的优越性逐渐被大量应用[2],中国风电行业正由集中式开发向集中开发与分散利用并举转变[3]。可预见分散式双馈风电机组(double fed induction generator,DFIG)在配电网中的渗透率将进一步提高[4]。DFIG同时含变流器(30%机组容量)接口和异步电机(与机组容量相当)接口,电网故障时会注入较大的短路电流。含DFIG配电网发生短路故障瞬间,分散式DFIG将产生一定的冲击电流影响配电网保护正常动作。因此,研究DFIG接入配电网的故障特性及短路电流计算方法,对电网运行控制及保护有重要的理论和实际意义[5]。
针对转子励磁和保护状态对DFIG机组短路电流特性的影响,文献[6]分别分析了考虑变流器持续励磁控制和Crowbar电阻投入控制两种策略DFIG短路电流暂态计算模型;文献[7-8]分别分析了含撬棒保护和直流卸荷保护的DFIG三相短路电流暂态计算模型,但未能考虑撬棒切除时刻对短路电流的影响;文献[9]推导了对称故障下计及网侧变流器的短路电流估算公式,但未考虑转子侧变流器无功补偿阶段对短路电流的影响。上述研究仅适用于电网发生对称故障情况,而电网中不对称故障发生频次远高于对称故障[10-11]。在此基础上,文献[12]分析了不对称情况下DFIG短路电流特性,但未能计及励磁变换器控制影响;文献[11]进一步考虑了DFIG低电压穿越(low voltage ride through,LVRT)运行控制策略,分析DFIG注入电流对风电场集电线路短路电流的影响,并给出集电线路相间和接地短路的电流保护整定方案。
在前述针对DFIG短路电流特性研究中,通常采用高阶DFIG模型和戴维南等效电路求解短路电流结果[13-15],该方式需要参数众多,参量间耦合关系复杂且计算量大,难以适应工程计算要求。从工程实用计算出发,文献[16]提出了考虑网侧和电机侧变流器控制的DFIG三相短路电流实用计算方法,但不适用于其不对称短路电流的计算;文献[17]提出在LVRT控制策略下的故障电流特性分析,但该方法仅考虑电源区别于传统同步发电机的特点,未重点考虑其DFIG的短路电流特性。
现将传统不对称短路电流计算的正序等效定则拓展至含DFIG配电网,推导计及不对称故障下DFIG负序电流注入的改进正序增广网络,归纳不同短路故障下DFIG接入点的短路阻抗、等值开路电压的正序和负序分量。同时,考虑撬棒保护电阻投切和DFIG低电压穿越控制,给出计及撬棒保护动作区域的DFIG不对称短路电流负序分量的计算曲面。在上述基础上,提出利用短路阻抗、等值开路电压的正序和负序分量等参数,通过对应的短路电流运算曲面得到DFIG不对称短路电流的计算方法。最后,在MATLAB/Simulink中进行仿真测试,验证所提方法的准确性。
1 含多台DFIG配电网不对称短路电流实用计算方法基本原理
在含多个风电场的大电网短路电流分析中,认为单个风电场内不同机组遭受的电压跌落幅度相近且暂态行为相似,忽略机组之间相互作用对短路电流结果的影响[17]。而在配电网中分散式DFIG常为单台接入,发生故障时,不同DFIG的端电压会呈现较为明显的差别,因此建模中需对每台DFIG进行单独考虑。从工程实用角度出发,同时类比对同步发电机的处理方式,对与某一时刻DFIG的短路电流模型,采用等值电流源的形式进行处理,即针对某一时刻的短路电流计算,将含DFIG配电网进行线性时不变的近似处理。
设辐射型配电网中节点1接入常规发电机,节点2~m1接入DFIG,如图1(a)所示,图中节点f为故障点。将故障点和不同类型发电机接入点保留,将第k台DFIG接入配电网的辐射形模型转换为三角形网络,并对k(k=2,3,…,m1)台DFIG的三角形网络进行叠加,得到如图1(b)所示的转移阻抗网络。由于考虑DFIG之间的交互影响将提高计算的复杂性,配电网主要电压支撑来源为上级主电源,其他DFIG注入电流对电压支撑作用小[18]。因此为简化计算,忽略机组之间相互作用对不对称短路电流的影响。利用图1(b)故障分量网络的节点阻抗矩阵Z,可得发电机节点1与故障点或DFIG接入点j的转移阻抗z′1j=z1Zjj/Z1j,其中Zjj和Z1j为矩阵Z的自阻抗和互阻抗,z1为发电机至节点1的等值阻抗。以第k台DFIG为例,形成短路电流计算等值网络[图1(c)]。

Zkf=z′kf;Z1f、Z1k为常规发电机至故障点、DFIG接入点转移阻抗并联后的等值阻抗

为常规发电机等值电压;为DFIG注入电网的正序、负序短路电流分量;和为故障点处序电流;ZΣ0为与DFIG升压变接线相关的零序阻抗

表1 附加电压与序电流系数δ表

(1)

(2)

(3)


图3 DFIG不对称短路电流等值电路

(4)
2 不对称故障DFIG短路电流负序分量计算方法
2.1 撬棒未投入时DFIG短路电流负序分量


(5)
式(5)中:
(6)



(7)

图4 4种控制方案下短路电流负序周期分量

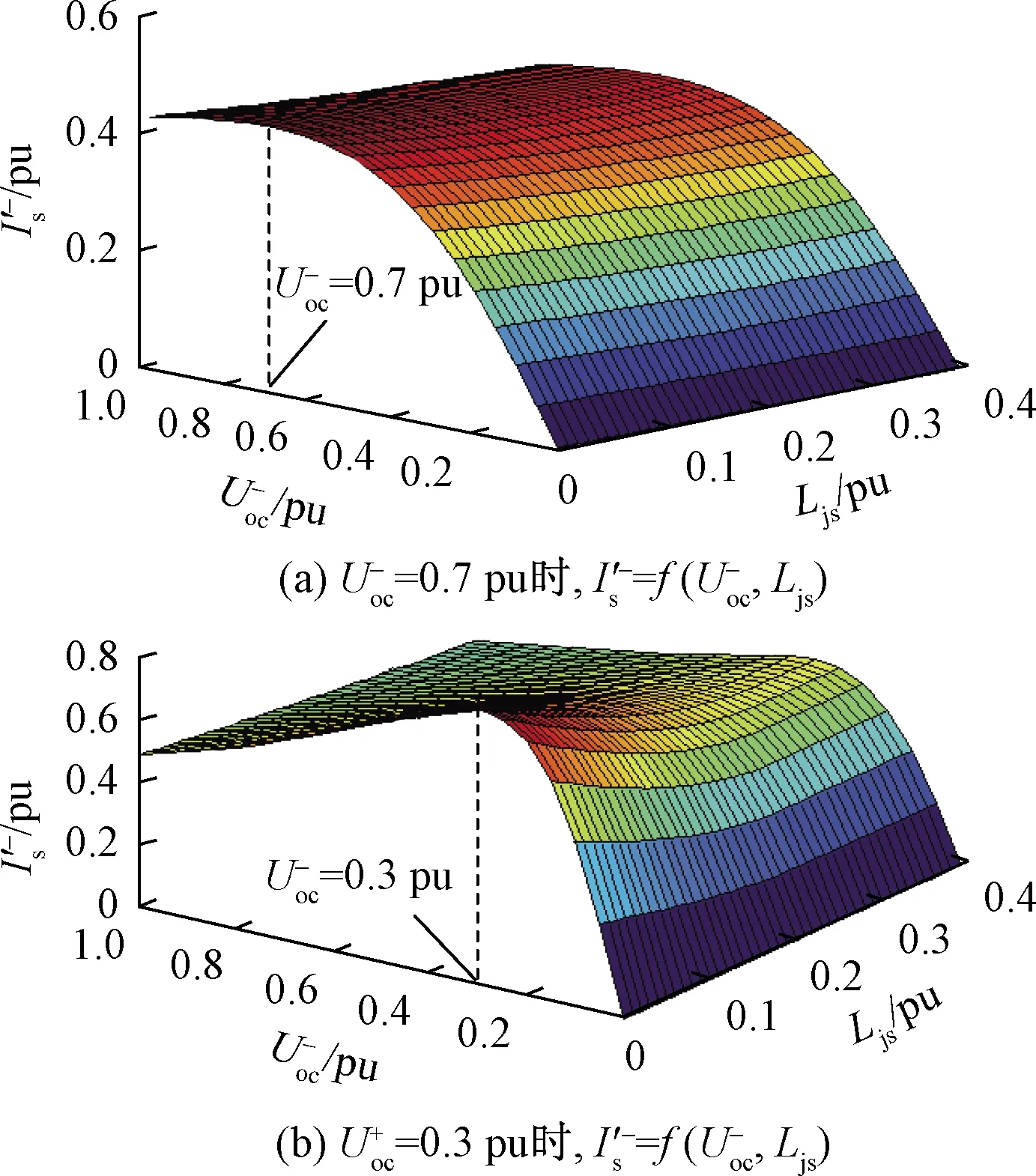
图5 撬棒保护未动作时短路电流负序周期分量
2.2 撬棒投入时DFIG短路电流负序分量
当撬棒投入后,相应戴维南等效过程与正序等效定则假设同撬棒未投入时一致,DFIG不对称短路电流负序分量的计算过程如下:由前述分析,不对称故障后DFIG定子磁链中存在对应强制分量,即正、负序定子磁链ψ′+s(t)、ψ′-s(t),以及直流衰减暂态分量ψsdc(t)[25]。同时,对定子磁链和转子磁链有ψs(t)=Lsis(t)+Lmir(t)和ψr(t)=Lrir(t)+Lmis(t),通过ψ′+s(t)、ψ′-s(t)可以得到对应的转子磁链正、负序分量ψ′+r(t)、ψ′-r(t)为
(8)
式(8)中:η′+和η′-分别为转子、定子磁链相关系数。撬棒投入后,由ψsdc(t)感应的定子磁链直流暂态分量ψrdc(t)为
(9)
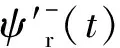
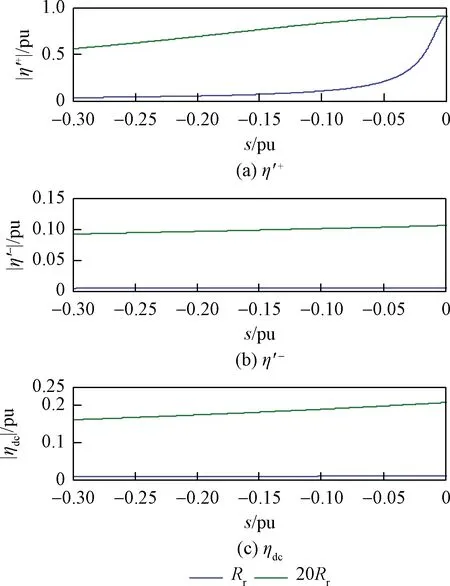
图6 转子和定子磁链相关系数
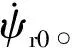

(10)

(11)


(12)
将计算电感Ljs加入定子绕组后,可得DFIG短路电流负序周期分量为
(13)
式(13)中:L′-s为DFIG负序等值电感。以1.5 MW的DFIG机组在计及撬棒投入情况为例,撬棒保护未投入(转子电阻为Rr)时,负序定子磁链相关系数η′-约为0,此时Ljs=σ(Ls+Ljs);当撬棒保护投入(等值电阻为20Rr)后,Ljs变化较大,两者负序等值电感如图7所示。由式(13)可知,撬棒投入后,DFIG不对称短路电流负序分量受发电机机端电压负序分量U′-s和负序等值电感Ljs影响。

图7 计及撬棒投入情况的负序等值电感


图8 撬棒动作后短路电流负序周期分量
3 DFIG撬棒动作区域及不对称短路电流计算步骤


图9 撬棒保护动作区域

图10 考虑撬棒动作情况的短路电流负序周期分量
DFIG接入配电网的不对称短路电流实用计算步骤如下。

步骤2 通过第2、3节画出第k台DFIG不对称短路电流负序周期分量的计算曲面(如图10所示),根据正负序等值电压及计算阻抗参数得到第k台DFIG的不对称短路电流负序分量I′-s。
步骤3 利用式(4)计算第k台DFIG在正序增广网络中的等值电压Uoc。
步骤4 利用等效阻抗Zjs等值电压Uoc和故障时刻t等参数,查找第k台DFIG三相短路电流运算曲面[15],得到第k台DFIG的不对称短路电流正序分量I′+s。

步骤6 将各DFIG短路电流的序分量代入图2的正序增广网络中,计算故障点短路电流正序分量的大小,利用正序等效定则得到故障相短路电流If。
修正系数推导如下。
针对第k台DFIG的不对称短路电流,设Ir为不对称短路电流仿真值,I′s为本文方法的计算值,γ为修正系数,Er为计算误差。由此可得
(14)
根据不同负序电压、正序电压和等效阻抗下的短路电流仿真与计算结果,可形成如下的修正系数矩阵Γ,表达式为
(15)
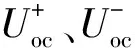
(16)
γ具体表达式由不同案例下归纳取平均值得到,再利用不同工况下的修正系数对计算结果进行修正,修正值为
(17)
则利用修正系数弥补计算误差的过程如下:通过计算,得到不同负序电压、正序电压和等效阻抗下第k台DFIG的不对称短路电流的仿真值与计算值,形成系数修正矩阵Γ,并确定相应正、负序修正参数表达式,利用上述修正系数对DFIG在不同工况下的短路电流计算结果进行修正,即可得到修正后的不对称短路电流。
4 仿真分析
以图11的含多DFIG配电网为例,通过本文方法计算不对称故障下各台DFIG故障后短路电流的周期分量,并与MATLAB/Simulink中DFIG电磁暂态过程仿真结果进行了比较。图11中,DFIG1、DFIG2的额定容量为1.5 MW,DFIG3、DFIG4的额定容量为2 MW,额定电压均为0.69 kV,设各DFIG出力为Pg0+jQg0=(1.0+j0)pu,转子转速为ωr=1.211 pu,其中撬棒电阻为20倍转子电阻、撬棒动作延时Tc为5 ms,转子电流控制参数kp=0.6、ki=8和Irlim=2 pu。各DFIG经风电升压变接入电网,其他机组参数见文献[20]。

图11 含多台DFIG配电网结构图


表2 节点6单相短路时短路电流未修正计算结果

图12 节点6单相短路机组正、负序短路电流


表3 节点6单相短路时DFIG3误差来源计算结果
通过仿真测试表明,DFIG短路电流采用运算曲面近似对误差贡献最大,然后是初始计算时假设DFIG未接入引入的计算误差,戴维南等值对误差贡献最小。为提高计算精度,确定图11的修正系数γ,图11所示系统中节点6发生a相单相短路时(故障持续时间0.06 s),在故障时间为0.01 s和0.02 s时,未经修正的短路电流计算结果如表4所示。

表4 节点5两相短路时未修正短路电流计算结果

由于上述修正参数系数表是针对本文所示算例及有限样本归纳得到,更为普适的修正参数系数表需要通过大量配电网算例仿真得出。

表时撬棒保护投入动作时部分修正系数
表6为节点5发生bc两相短路时(故障持续时间0.06 s),各DFIG短路电流正序与负序分量的修正计算值、仿真值结果。不对称故障发生后,除DFIG4撬棒保护动作外,其余3台DFIG均保持不脱网运行、撬棒保护不动作,且每台DFIG转子侧变流器采用以消除电磁功率波动为目标的控制方式。节点5发生bc相不对称故障后,撬棒未投入机组的负序电流由变流器励磁控制产生,表6中DFIG1至DFIG3的短路电流负序分量均小于0.2 pu,而撬棒投入的DFIG4短路电流负序分量较其余3台明显增加。不论撬棒投切情况,根据表6,经过修正系数后正、负短路电流计算值与仿真值误差在(-7%,5%),其误差值均小于原未经修正系数修正时的误差。但同时需要注意的是,实际风电机组参数与仿真模型参数之间也存在一定差别,该部分误差具体为各种不确定因素导致的系统参数误差,其绝对值和符号均不可预测,该部分误差消除困难。对此可以采用继电保护整定中的可靠系数,通过引入可靠系数确保短路电流计算结果相对保守。

表6 节点5两相短路时修正后短路电流计算结果
5 结论
将正序等效定则拓展至含DFIG配电网的不对称短路电流计算,提出了计及负序电流注入的分散式DFIG接入配电网的不对称短路电流实用计算方法。利用MATLAB/Simulink对本文方法进行仿真测试,结果表明,本文方法利用等效阻抗和正、负序等效电压参数,通过对应的短路电流运算曲面得到DFIG不对称短路电流结果,降低了含DFIG配电网不对称短路电流的计算难度,适用于工程中DFIG不对称短路电流计算;本文方法主要误差来源于DFIG短路电流的运算曲面近似和初始计算时设DFIG未接入计算等值开路电压的正序和负序分量,但通过引入修正系数可将短路电流计算结果误差控制在可接受范围内。下一步将针对工程实践验证本文方法的可用性、确定可靠系数合理取值等方面继续开展研究。

