Maximum-Profit Advertising Strategy Using Crowdsensing Trajectory Data

LOU Kaihao, YANG Yongjian, YANG Funing, ZHANG Xingliang

(1.Jilin University, Changchun 130012, China；2.China Mobile Group Jilin Co.,Ltd.,Changchun 130021,China)

Abstract: Out-door billboard advertising plays an important role in attracting potential customers.However, whether a customer can be attracted is influenced by many factors, such as the probability that he/she sees the billboard,the degree of his/her interest,and the detour distance for buying the product.Taking the above factors into account, we propose advertising strategies for selecting an effective set of billboards under the advertising budget to maximize commercial profit.By using the data collected by Mobile Crowdsensing (MCS), we extract potential customers’implicit information, such as their trajectories and preferences.We then study the billboard selection problem under two situations,where the advertiser may have only one or multiple products.When only one kind of product needs advertising, the billboard selection problem is formulated as the probabilistic set coverage problem.We propose two heuristic advertising strategies to greedily select advertising billboards,which achieves the expected maximum commercial profit with the lowest cost.When the advertiser has multiple products, we formulate the problem as searching for an optimal solution and adopt the simulated annealing algorithm to search for global optimum instead of local optimum.Extensive experiments based on three real-world data sets verify that our proposed advertising strategies can achieve the superior commercial profit compared with the state-of-the-art strategies.

Keywords:billboard advertising;mobile Crowdsensing;probabilistic set coverage problem;simulated annealing;optimization problem

1 Introduction

Out-door billboards are one of the most effective tools for advertising.According to PQ Media[1],global digital roadside billboard advertising industry grew by a large margin in 2017; specifically, digital roadside billboard advertising sales have increased by 10% to a total amount of 3.2 billion dollars in the US.Compared with other advertising methods, the out-door billboard can easily make a deeper impression on potential customers, since it provides the strong visual impact, long placement duration and rich information content.

By advertising on out-door billboards, an advertiser can attract potential customers for his/her products.For some products or activities such as temporary promotion, potential customers may immediately decide whether to go to the shop to purchase products after seeing the advertisement.In this situation, once a potential customer is attracted by the advertisement on the billboard, he/she will purchase the relative product and the advertiser will obtain the commercial profit.However, due to the advertising budget constraint, an advertiser cannot advertise on all the available billboards.Hence, an advertiser should decide which billboards to do advertising to attract as many potential customers as possible,in order to maximize the commercial profit.Note that whether a billboard can attract a customer is determined by many factors, such as customers’mobility (whether they can see the billboard),customers’preferences (whether they are interested in the product),and the location to buy the product (the detour distance).More importantly, all the above information is privacy-sensitive, especially for the customers’trajectories and preferences,which greatly limits the billboard advertising research.

Most of the existing advertising strategies focus on what advertising content should be delivered and how to select locations for the static roadside billboards, but they do not jointly take potential customers’mobility, preferences and detour distance into consideration.In Ref.[3], NIGAM et al.decide the locations of billboards by using the data collected by radio frequency identification (RFID).In Refs.[4] and [5], the advertisers can select the billboard locations by using GPS and phone data.Besides, in Refs.[6] and [7], the advertising content on the billboard is determined by the potential customers’preferences or their detour distance.All these existing works do not jointly take potential customers’mobility,preferences and detour distance into consideration, which results in the advertiser failing to accurately quantify the commercial profit of the available billboards and thus prevents the corresponding strategies from achieving the maximal commercial profit.

▲Figure 1.Problem description of billboard advertising,where the advertiser has only one kind of product

In this paper, we focus on a billboard advertising scenario,which is shown in Fig.1.There are four available billboards placed at different locations.Two potential customers unconsciously move among the billboard locations.An advertiser wants to do advertising for a product with a limited budget(400 in Fig.1)and that is not enough to place advertisements on all billboards.Each billboard has an advertising cost (e.g.,b1=150, etc.)and also a potential profit.The profit is measured quantitatively by the expected number of attracted customers.Obviously, whether a potential customer is attracted by the billboard is influenced by many factors, such as the probability that the customer can see the billboard, the degree of his/her interest in billboard advertising, and the detour distance that he/she goes to buy the product.We use the detour distance as an example to describe our problem (Fig.1).Under a total budget of 400, the advertiser can at most cover the costs of two billboards.Two example plans show the different advertising strategies: Plan 1 advertises at billboards b1 and b3,while plan 2 advertises at billboards b2 and b4.If the purpose is to minimize the detour distance, obviously plan 1 is better than plan 2.But actually, only using detour distance is not comprehensive, as described above, and many factors should be taken into consideration when we measure a billboard’s potential profit.For example, if customers A and B cannot pass by the billboards b1 and b3, but they can pass by the billboards b2 and b4, plan 2 is better for this situation.Hence, in order to maximize the commercial profit under the limited budget, this paper focuses on the problem of selecting billboards with the consideration of multiple factors, which can affect the probabilities of customers being attracted.

To solve the above billboard selection problem, we need to collect the potential customers’preferences, mobility patterns and their detour distance, which are privacy-sensitive.Hence,how to collect the potential customers’preferences, mobility patterns and their detour distance is the first challenge.Moreover, the advertiser needs to accurately quantify the expected commercial profit of each billboard to decide which billboards to do advertising,which is the second challenge.When the advertiser has multiple products to advertise, it is essential to make rational use of the budget and a reasonable distribution of advertisements,which is the third challenge.

In this paper, we normalize the influences of the above three factors, formulate the billboard selection problem as a probabilistic set coverage problem, and propose some effective advertising strategies to address this problem.First, we adopt Mobile Crowdsensing (MCS)[8-10]to collect the privacy-sensitive customer profiles[6,11]including their vehicular trajectories and preferences.For example, if a user has performed some sensing tasks for an MCS application, the application may record his/her GPS trajectories during his/her working time.Also, the user’s historical information can be used to infer his/her preferences for the advertising[11].For example, if a user has completed many tasks near the food market, the food market may be considered as a preference of this user.Based on their vehicular trajectories and the location of the advertiser’s shop, we can estimate the potential customers’detour distance for purchasing the product.With the information, we then study the advertising problem under two situations, where the advertiser may have only one or multiple products.For the first situation where the advertiser has only one kind of product to advertise, we propose two heuristic advertising strategies to greedily choose advertising billboards,which can maximize the total expected commercial profit for the advertiser.For the second situation where the advertiser has multiple products, we adopt the simulated annealing algorithm to search the global optimum instead of local optimum.

The main contributions of this paper are summarized as follows:

·We formulate this billboard advertising problem as a non-deterministic polynomial (NP)-hard problem to select appropriate billboards for the advertiser to achieve the maximum commercial profit with the constraint of budget.We design our advertising strategies with consideration of customers’mobility,preferences and detour distance.

· For the situation where the advertiser has only one kind of product to advertise, we propose two bounded heuristic advertising strategies,whose approximation ratios are

· For the other situation where the advertiser has multiple products to advertise, we propose an advertising strategy by using the simulated annealing algorithm to search the global optimum.

· We conduct extensive simulations based on three real-world trajectories: roma/taxi[12], epfl[13], and geolife[14].The results show that compared with other strategies,our advertising strategies can achieve superior commercial profit for the advertiser.

The remainder of this paper is organized as follows.We review the related work in Section 2.We describe the system models and formulate this billboard selection problem in Section 3.We describe the general technologies we used in Section 4.The detailed advertising strategies are proposed in Section 5.In Section 6, we conduct the simulations to determine the performances of our advertising strategies.We conclude this paper in Section 7.

2 Related Work

2.1 Advertising Strategy

There have been many works on advertising strategy.In Ref.[6], WANG et al.propose a utility-evaluation-based optimal searching approach to empower audience targeted billboard advertising by using vehicle trajectory data with consideration of audiences’interests.In Ref.[7], ZHENG et al.study a promising application in Vehicular Cyber-Physical Systems (VCPS)to attract potential customers for the shopkeeper by using Roadside Access Points (RAPs).In Ref.[3],NIGAM et al.present the design and implementation of an intelligent advertising system which is integrated in a network and can be used in many retail stores, shopping malls and shopping centers.In Ref.[4], LIU et al.propose a system which uses taxi trajectories to help select the locations of billboards.In Ref.[5], HUANG et al.propose a strategy to maximize the coverage of advertisements with consideration of individuals’interests and mobility patterns.In Ref.[15], KRISHNA et al.develop a new application for detecting significant billboards for adults and older people in street-laying areas.In Ref.[16], AN et al.propose an advertisement system for enhancing the efficiency of advertisement by using the Wi-Fi union mechanism.In Ref.[17], ZHANG et al.optimize the influence of outdoor advertising with the consideration of impression counts.They propose a tangent line based algorithm to select roadside billboards for maximizing the influence of outdoor advertising.

Different from the research works mentioned above where the authors do not jointly take potential customers’mobility,preferences and detour distance into consideration, in this paper, we focus on the problem of selecting billboards with the consideration of the above factors, in order to maximize the commercial profit for an advertiser.

2.2 Mobile Crowdsensing

There have also been some works focusing on mobile crowdsensing.In Ref.[11], KARALIOPOULOS et al.draw on logistic-regression techniques from machine learning to learn users’individual preferences from past data in Mobile Crowdsensing.In Ref.[18], ARIYA SANJAYA et al.present an application program, which provides data for SOROT (Citizen Reporting MCS Application)platform by analyzing citizen participation, and speeds up the solution of urban problems.In Ref.[19],CHEUNG et al.propose an algorithm for calculating the optimal user decision-making under general conditions by using the dynamic programming method.Based on the gametheory approach, CAO et al.in Ref.[20] propose an incentive mechanism in order to encourage mobile devices to share their own resource to perform sensing tasks cooperatively.In Ref.[21], GONG et al.focus on the path planning and task assignment problem in Mobile Crowdsensing, so that the total task quality can be maximized with the constraints of user travel distance and budget.In Ref.[22], MARJANOVIĆ et al.propose an edge computing architecture, which is suitable for large-scale MCS services by putting the main MCS functions in the reference of MEC architecture.For truth discovery in mobile crowdsensing, ZHENG et al.in Ref.[23] propose two novel privacy-aware crowdsensing designs with truth discovery so that the bandwidth and computation performance on individual users can be significantly improved.In Ref.[24],WANG et al.propose a two-stage solution to the heterogeneous multi-task assignment (HMTA)problem, which utilizes the implicit spatiotemporal correlation between heterogeneous tasks to effectively handle multiple concurrent tasks in shared resource pools.In Ref.[25], WANG et al.propose a new framework of participatory perceptual multi-task allocation,which coordinates the allocation of multiple tasks on the multitask PS platform to maximize the overall effectiveness of the system.

These works we mention above focus on different areas of mobile crowdsensing, while we attempt to extract potential customers’implicit information, such as their trajectories and preferences, by using the MCS data, in order to select appropriate billboards for the advertiser.

3 System Model and Problem Formulation

3.1 System Model

Consider that there is an advertising system which is composed of a crowd of potential customers, denoted by the setU={u1,u2,...,un} and a set of available billboardsV={v1,v2,...,vm}.The costs of available billboards are denoted byC={c1,c2,...,cm}.The different areas in the map can be represented asL={l1,l2,...,lh}.All billboards are located at different areas and each area has only one billboard.Moreover, the preference types are denoted by the setA={a1,a2,...,aj}.Hence,without the loss of generality,we denote the preferences of potential customeruiasAui⊆A.We suppose that each kind of products has an advertisement which can be denoted byT={t1,t2,...,tr}, and the attributes of producttxcan be denoted byAtx⊆A.Meanwhile, each billboard is available for only one advertisement.

In our scenario,at the beginning,each potential customeruistarts moving from his/her initial location, and goes to his/her destination.Every time a potential customer sees an advertisement for a product,he/she will decide whether to buy the product.The detour distance is an important factor affecting the customer’s decision, and then we used(ui)to denote the detour distance forui,which represents how much more distanceuineeds to go than his/her original route for buying the product.If a potential customer has been attracted to buy the product, this customer cannot be attracted by the same advertisement again.In other words,each potential customer can be attracted by a product at most once.The attracted customers are denoted byUattr.

3.2 Problem Description

With the limit of budget, which is denoted byB, we attempt to choose a set of billboards denoted byS={s1,s2,...,sk}fromVfor advertising.When the advertiser has multiple products,we also need to choose the advertisements for the selected billboards to maximize the commercial profit.In this paper, we suppose that if a billboardviis selected inS,then it will deliver advertisement content to those potential customers whose locations are in its area until the deadline.The deadline is how long the advertiser can use a billboard, and we suppose that all billboards have the same deadline.Our purpose is to find the best advertising strategy for the following billboard selection problem:

whereFis the total commercial profit for the advertiser from billboard advertising.The problem is that an advertiser should attract potential customers as many as possible with limited budgetB.In this paper, we assume that if a customer is attracted after he/she sees the advertisement,then the advertiser will obtain a profit from the customer.If a potential customer is attracted by an advertisementtx, the profit that the advertiser can get is denoted byandφ=1.If the customer is not attracted,φ=0.In order to reduce the complexity of the calculation,we suppose that the customers attracted by the same advertisements can create the same profit for the advertiser, and the customers attracted by the different advertisements may create different profits for the advertiser.In other words,it can be denoted by∀tx∈T, ∀ty∈T.Our advertising strategies aim at finding the best set of billboards to deliver the advertisements, so that the commercial profit for the advertiser is maximized, with the constraint that the total costs of selected billboards should be less or equal to the budget.

3.3 NP-Hard Proof

Before solving the above optimization problem, we first attempt to prove that the billboard selection problem is NPhard,which is shown as follows:

First of all,we formulate this problem in Eq.(1)as the probabilistic set coverage problem, which includes a collection of element setsX={X1,X2,...,Xm} with the corresponding costsc={c1,c2,...,cm}.Xiconsists of a lot of elements, which is denoted byO={O1,O2,...,On}.The associated possibilities that the elements can be covered are denoted byp={p1,p2,...,pn}and the associated weights of elements are denoted byW={w1,w2,...,wn}.The objective is to select a subcollection ofXunder the budget constraintBto maximize the weights of covered elements.

Then, we reconsider the billboard selection problem in this paper.First of all, we consider the situation where the advertiser has only one type of product.Since the commercial profit depends on the number of attracted customers, we can regard the potential customers as the element setO.The probabilities that the potential customers decide to buy the product when they see the advertisement can be regarded asp.The profit that the advertiser gets from each customer can be considered asW.We can regard the billboard set we need to choose asX,and the total costs of selected billboards can be regarded asc.We need to select the billboards to attract as many potential customers as possible, hence the billboard selection problem can be regarded as the probabilistic set coverage problem.Since the probabilistic set coverage problem is NP-hard, the billboard selection problem when the advertiser has only one type of product is NP-hard.Moreover, when the advertiser has multiple products to do advertising, the selection problem becomes more complicated, since we should not only consider how to select billboards but also the advertisement placed on the billboard.Hence, under this situation where the advertiser has multiple products, the billboard selection problem is also NP-hard.

4 General Technologies

4.1 Single-Product

In this section,we consider the situation where the advertiser needs to advertise for only one kind of product and potential customers need to decide whether to go to buy the product every time they see the advertisement.We useTto denote the advertisement of the product for ease of calculation and each attracted customer can create the same profitffor the advertiser in this section.We first discuss how to predict the potential customers’mobility patterns.Then, we quantify the influences of customers’preferences and detour distance on customers’attraction probabilities, respectively.Finally, we quantify the utilities of different billboards.

4.1.1 Mobility Prediction

First of all, we attempt to predict each potential customer’s location so that we can select the appropriate billboards to improve the effectiveness of advertising.It is not difficult to map each customer’s trajectories into a square area in a plane region, especially when the area is small[26].Thus, we can grid the area in the map like Fig.1 and convert each customer’s trace into a sequence of grids, in order to reduce the difficulty of calculation.After we grid the map,the billboards’locations can be converted into fixed grids.We assume that, if a potential customer enters a grid which has a selected billboard, he/she will see the advertisement and decide whether to buy the product.In this paper, we adopt the semi-markov model[27-29]to predict the customers’mobility.One of the most important equations of semi-markov,Z(·)is defined by Eq.(2).

whereZu(li,lj,X)is the probability that the customeruwill move from his/her current gridlito the gridljat or before timeXwhen he/she moves next time.represents the customeru’sk-th location during his/her moving and its corresponding arrival time is denoted asThe grid that the customer will enter in the next time unit is related to his/her current grid, which can be obtained from the customer’s historical trace records.Then, we can define another key equationQ(·),denoted by Eq.(3).

Q(·)denotes the probability of a potential customerumoving acrossljfromlibefore time slotX.It is easy to find that the potential customers cannot move from one grid to another whenX=0, which is reasonable, so we can getQu(li,li,0)= 1 andQu(li,lj,0)= 0,(i≠j).Next, we calculate the probability of a customer passing any gridljbefore deadlineXas follows:

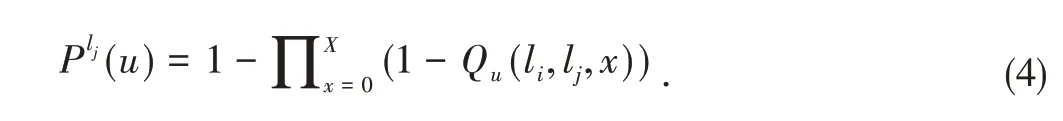
4.1.2 Customer Preference Level

After considering customers’mobility, in order to determine the expected commercial profit of each billboard, we need to measure a potential customerui’s preference level for the productT, which is denoted asPprefer(ui).First, we collect the customerui’s preferencesAuiand the productT’s attributesATwhere⊆AandAT⊆A.Then the preference levelPprefercan be calculated by the following equation:

Obviously, if the product’s attributesATcan match all the customer’s preferences, thenPprefer=1, which means the potential customeruiwould be likely to buy the product by the factor of preferences.

4.1.3 Detour Distance

In the single-product scenario, the potential customer may change his/her trajectory if he/she is attracted by the advertisement.Hence, as mentioned above, another factor that the customeruiwill consider when he/she decides whether to buy a product is the detour distance, which is denoted byd(ui).We first use Euclidean distance to measure potential customer’s path length.As we can see from the Fig.1, the original path for the customer A isd1+d2 +d3.When the customer A sees the advertisement from the billboard b1, which is selected for advertising,he/she will decide whether to go to the shop for buying the product.If he/she is attracted to buy the product, the path to the shop isd4, and the path from the shop to his/her original destination isd5.The detour distance can be calculated as follows:

During the path, the customer may see a lot of billboards that have been chosen for advertising, so he/she will decide whether to buy the product after he/she sees a selected billboard.Hence, the detour distance should be calculated as the distance from the current billboard to the customer’s destination.Then we need to measure how the detour distance affects the probability that the customer would go to the shop.The equation is shown as follows:

whereDmaxis a predefined threshold andPdetour(ui)represents the detour distance level which affects the probability that the customer will be attracted to buy the product.In this paper,we setDmaxas the maximum diagonal length in the selected area.It is not difficult to find that the less the detour distance is,the higher chance that the customer will go to the shop for buying the product,which is reasonable.

4.1.4 Billboard Utility

In this part, we use utility to represent the expected commercial profit of a billboardvj, which is denoted byF(vj).F(vj)is the expected commercial profit that the billboardvjcan bring to the advertiser.First of all, we need to calculate the probability that the customer will be attracted to buy the product after he/she sees the advertisement, the equation of which is shown as follows:

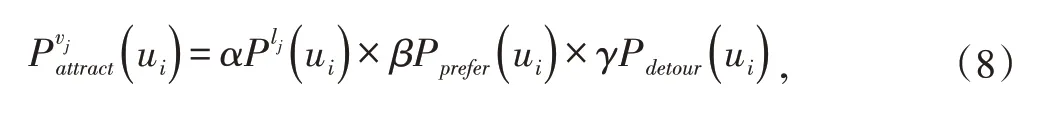
whereljis the grid that the billboardvjis located.α,βandγare relative weights whereα+β+γ=1.By now, the probability that the customer will be attracted to buy the product after he/she sees the advertisement is obtained.Besides, the probability that the customer will be attracted to buy the product can be affected by the different billboards that the customer sees.Therefore, it is necessary to determine the influences of different billboards on the same potential customer, which can be denoted as follows:

wherePattract(ui)is the probability that the customeruiwill be attracted to the shop after he/she sees the current billboard with consideration of different billboards’impacts.In other words,Pattract(ui)is the probability that the potential customer will decide to buy the product at least once when he/she sees the same advertisement many times.Then the utility of a billboard for a specific advertisement can be calculated as follows:

Then we can get the total utility of the billboard set, which in shown in Eq.(11):

4.2 Multi-Product

In this subsection, we consider the situation where the advertiser may have multiple products and potential customers do not need to go to the shop immediately to buy products.In other words,the potential customer will not change his/her trajectory if he/she is attracted by the advertisement.We suppose that each product has a corresponding advertisementT={t1,t2,...,tr}and each advertisement of a product attracts a customer with different commercial profit which can be denoted asη={f1,f2,...,fr}.Each billboard can only be selected for one advertisement.For example, as shown in Fig.2, there are four available billboards (b1-b4)placed at different locations.Two potential customers are unconsciously moving among the billboard locations.The advertiser wants to do advertising for three different products (Type 1-3)while he/she has a limited budget (500 in Fig.2), and that is not enough to place the advertisements on all billboards.Each billboard has an advertising cost (e.g., b1=150, etc.)and also an expected commercial profit.Two example plans show the different advertising strategies under the budget constraint.Plan 1 advertises at billboards b1,b2 and b4 for products 1,2 and 3,while plan 2 advertises at billboards b1, b2 and b3 for products 3, 1 and 2.In order to maximize the profit within the limited budget, the advertiser needs to determine which plan is better.Next,we will discuss how to address this problem.

4.2.1 Mobility Prediction

First of all, we still consider how to predict customers’mobility patterns.Due to the reason that potential customers’mobility patterns wouldn’t be affected by the number of products, the mobility prediction method we proposed earlier can be applied for this situation.

4.2.2 Customer Preference Level

Next,we will discuss how to determine the customers’preference level in this part.Since the advertiser has multiple products which have different attributes, it is not difficult for us to find that we can reformulate Eq.(5)as follows:

whereAuidenotes the preferences of a customeruiandAtxdenotes the attributes of producttx.It is obvious that the more the product’s attributes match the customer’s preferences,the more likely that the customer will decide to buy the corresponding product.

4.2.3 Billboard Utility

In this situation, potential customers do not need to go to the shop immediately to buy products, hence, we can ignore the influence of detour distance on customers’decisions.As a result, the probability that the customer will be attracted can be reformulated as follows:

whereljis the grid where the billboardvjis located.αandβare relative weights whereα+β=1.Since different products have different attributes, we consider there is no competition among different products and the probabilities of a potential customer buying different products are independent.In other words, a customer’s purchase of one product does not affect the possibility of buying another different product.Hence,each customer can be attracted by different products and bring more commercial profit to the advertiser.

The utility of a billboard for a specific advertisementtxcan be calculated as follows:

Then we can get the total utility of the billboard set, which is shown as follows:

5 Advertising Strategies

5.1 Single-Product

In this section, we propose two heuristic advertising strategies to address the billboard selection problem for the situation where the advertiser has only one kind of product to advertise.

5.1.1 Same Cost for Each Billboard

First of all, we consider the situation where all billboards have the same cost.In this situation, we can convert the budget restriction into the billboard’s quantity restriction where we need to select a billboard set to maximize the profit for the advertiser with the constraint of billboard numberk.The detailed greedy algorithm Advertising Strategy for Constant Cost(ASFCC)is shown in Algorithm 1.

▲Figure 2.Problem description of billboard advertising,when the advertiser has multiple products

In Algorithm 1, we select the billboard which has the largest utility at the beginning of the algorithm.Then,we continue selecting the billboard, which can maximize the value of the total utilityFto be the second billboard among the other billboards and add it intoS.This process will be executed forktimes until the number of billboards which have been selected meets the requirements or all the billboards have been selected.The reason why we do not select the billboard with the current largest utility is that the local optimal solution is not necessarily the global optimal solution.For example, consider that there are three billboardsa,b,cand two customersu1,u2.Billboardsaandbmay attract customeru1with probabilities 1 and 0.8.Billboardcmay attract customeru2with probability 0.5.Since each attracted customer can create the same profit for the advertiser, it is obvious that we should select the billboardsaandcto achieve the maximum commercial profit.

By now, we have proposed a greedy advertising strategy to address the above NP-hard problem.According to Ref.[30],we can confirm thatFis a submodular function, which can be summarized as follows: consider that there are two arbitrary node setsS1andS2,S1⊂S2,and ∀vk∈V∖S,the submodular property holds, i.e.,The bound can also be derived from Ref.[30],which is

5.1.2 Different Costs for Each Billboard

Now, we attempt to propose another heuristic advertising strategy Advertising Strategy for Different Costs (ASFDC)for the situation where all billboards have different costs.As we can see from Algorithm 2,the exhaustive method is used to determine the billboard setS1which has the largest expected commercial profit wherekis the quantity restriction.Then we execute the greedy process until the budget is lower than the lowest cost of available billboards or all the billboards have been selected to theS2.At last, we compare the utility of billboard setS1with the utility of billboard setS2to determine which is larger to be the final result.

By now, we have proposed another advertising strategy to address the billboard selection problem when all billboards have different costs.According to Ref.[31],we can getF(Sj)≥which represents that whenk≥3, the approximation ratio for this algorithm is

5.2 Multi-Product

We have described the scenario of the situation where the advertiser has multiple products to advertise, which is more difficult than the situation in Section 4.In order to address this problem, we attempt to adopt the simulated annealing algorithm.In this situation, we consider that all billboards have different costs and the same billboard would cost the same for different products.

First of all, we modify the algorithm ASFDC so that it can be applied in this situation, which is shown in Algorithm 3.The difference is that we need to calculate the utilities of each billboard for different products in each iteration, and then we select the billboard with the advertisement which can maximize the total expected commercial profit.This process will be repeated until we run out of the budget.Then we take the result obtained in the previous step as the initial solution of the simulated annealing algorithm Advertising Strategy for Multiadvertisement with Different Costs (ASFMDC), which is shown in Algorithm 4.

In Algorithm 4, we first select a billboard to delete from the selected billboard setSand then select a billboard from the available billboards inVto generate a new solutionS′(lines 3-5).Next,we compare the expected commercial profit ofS′with that ofSto determine which solution should be accepted in the next iteration (lines 6-9).Then,we compare the expected commercial profit of the current solution with the current best solution to update the current best solution (lines 10-11).The temperatureTempis updated at each iteration (lines 11-15).Next, we will discuss the method of removal and insertion we used in Algorithm 4,as well as the stopping conditions.

5.2.1 Billboard Removal Method

We adopt two methods to decide which billboards to delete,which are described as follows:

· Random removal: we randomly select a billboard from the selected billboard setS,and remove it.

· Probability removal: we calculate the expected commercial profit of each selected billboard and remove one of them with probability.The higher the expected profit is, the lower the probability of removal would be.

5.2.2 Billboard Insertion Method

We also design two methods to determine which billboards to insert and the advertisements on the billboards.The detailed description is as follows:

· Probability Insertion: we calculate the expected commercial profit of each available billboard, and select one of them with probability to add to the selected billboard setS.The higher the expected profit is, the higher the probability of insertion would be.

·Expectation Maximization Insertion:we calculate the expected commercial profit of each available billboard, and select one of them with the max expected profit to insert to the billboard setS.

For a better understanding, we provide an example: as shown in Table.1,there are two available billboards and three different advertisements.The expected profit has been calculated and shown in the table.First of all, we consider the advertisement that brings the maximum expected profit for each billboard as the final advertisement for that corresponding billboard.Obviously, the final advertisement for billboardAshould be advertisement 3,and the final advertisement for billboardBshould be advertisement 1.If Probability Insertion is adopted, then we should normalize the expected profit.Thus,the probability for selecting billboardAis 47,and the probability for selecting billboardBis 37.On the other hand, if Expectation Maximization Insertion is adopted, then we will select the billboard with the maximum expected profit, i.e.,the billboardAin this example.The process of removal is similar to that of insertion.

We use a multi-thread approach to improve the experimental performance which combines the above removal and insertion methods.As a result, we can create four threads with different combinations of removal and insertion.

5.2.3 Stopping Conditions

We determine two stopping conditions in our simulations,which are listed as follows:

· The maximum number of iterations is set to 1 000 000, and when the iteration number exceeds the limited number,the algorithm would stop.

· The maximum number of iterations without improving is set to 100 000, which means after 100 000 iterations, if the result is not improved,the algorithm would stop.

6 Performance Evaluation

6.1 Simulation Traces and Settings

In this paper, three real-world datasets, the roma/taxi trace set[12], epfl trace set[13]and geolife trace set[14], are adopted to verify the performances of our proposed strategies.In the roma/taxi trace set, 320 taxi drivers that work in the center of Rome are included.The traces in this dataset represent the positions of those taxi drivers, which are collected every 7 seconds and sent to a central server.In the epfl trace set, about 500 taxis’GPS coordinates are included which are collected over 30 days in the San Francisco Bay Area.Each taxi is equipped with a GPS receiver and sends a location-update toa central server.The records are fine-grained so that we can accurately interpolate user positions between location-updates.In the geolife trace set, there are 17 621 trajectories whose total distance is about 1.2×106km.The total duration of this dataset is about 48 000 h which are collected by different GPS loggers and phones.

▼Table 1.An example for removing and inserting billboards

First of all, we process the dataset by filtering out some abnormal users including those with discontinuous traces or remote locations.Next,we match these traces into a map area and convert it into a gridded map, which are processed by Baidu Map application programming interface (API).We randomly select a supermarket or a mall in the city as the advertiser’s shop and we also select 35 billboards located in different areas to be the candidate billboards.

For the first situation where the advertiser has only one kind of product, we set theα,βandγin Eq.(8)to 13.The preferences of each customer are randomly generated to reduce the difficulty, but they can also be inferred from each customer’s historical information, which is not the focus of this paper.The total number of preference types |A|= 20.The deadline is set from 500 to 600.The costs of billboards are set to 10 when the costs are constant and the costs of billboards are set from 10 to 20 when the costs are different.The budget is set from 50 to 170 when the costs are constant and it is set from 100 to 200 when the costs are different.The number of each customer’s preferences is set from 5 to 15 in our simulations.Each attracted customer can bring a profit of 10 to the advertiser.We repeat our simulation 10 000 times, taking the average result as the final result.

For the situation where the advertiser has multiple products, we set the deadline in the simulation from 150 to 250.We set theαandβin Eq.(13)to 12.The budget in this situation is set from 100 to 200 and the profit per attracted customer for each product is set from 10 to 30.We setθ=0.999,Temp=10 000 andTempmax=10 000.The other experimental parameters are the same as those when the costs are different for the single-product scene.In this paper, we take the total commercial profit as the evaluation metric to measure the performances of different strategies.

6.2 Strategies for Comparison and Metric

For the first situation where the advertiser has only one kind of product, in order to determine the performances of our advertising strategies, we compare the ASFCC with ASFCCBasic,Random and Capped Greedy (CG)[7]when all billboards have the same cost.ASFCC-Basic would select the billboards which have the largest commercial profit, and Random would randomly select the billboards for advertising.The CG would select the billboards, which can maximize the total commercial profit of selected billboards without consideration of customers’preferences.

When all billboards have different costs, we compare ASFDC with ASFDC-Basic and Random, where ASFDC-Basic would choose the billboards which have the largest commercial profit for advertising.Random would randomly select the billboards with the limit of budget.

For the other situation where the advertiser has multiple products,we compare the ASFMDC and ASFDADC with ASFDADC-Basic and Random, where ASFDADC-Basic would choose the billboards with the largest commercial profit.The other strategy Random would randomly select the billboards and their advertisements.

We use the commercial profit as the metric to measure the performances of different advertising strategies.When an advertising strategy performs better, it would have higher commercial profit, which is reasonable.In order to calculate the commercial profit, we need to judge whether a customer is attracted to purchase a product.When a potential customer sees an advertisement on a billboard, he/she has a chance to buy the product in the advertisement.After the deadline of the whole experiment, each potential customer has different purchase probabilities for each product.Through these probabilities, we can use a random number generator to repeatedly test whether a potential customer has bought products, and finally we can get the commercial profit by averaging the payment of potential customers.

6.3 Simulation Results for Single-Product with Constant Billboard Cost

In this section, we aim to test the performance of the proposed strategy ASFCC, when all available billboards have the same cost.In this situation, the advertiser only needs to determine whichkbillboards to select for advertising.Hence, we compare our advertising strategy ASFCC with ASFCC-Basic,Random and CG on three datasets.The results of the simulation are shown in Figs.3,4 and 5.

First of all, we evaluate the performances of the above four strategies on the roma/taxi trace set.As illustrated in Fig.3,we investigate the influence of the four variables on the total commercial profit of different strategies.Obviously, ASFCC can achieve the maximum commercial profit for the advertiser,while the performance of Random is the worst.We can find that the total commercial profit increases with the growth of deadline, which represents the duration of billboard advertising.It is reasonable for this phenomenon, because when the deadline increases, the selected billboards may have more chances to attract the potential customers so that the commercial profit may increase.We can also find that the total commercial profit shows an upward trend with the increase of budget.The reason is that with the budget increasing,the advertiser can select more billboards for advertising so that more potential customers may be attracted.By changing the number of customers’preferences, we can see that the performances of ASFCC and CG are very close but far better than those of ASFCC-Basic and Random.

▲Figure 3.Performances on the roma/taxi trace set,when all billboards have the same cost

▲Figure 4.Performances on the epfl trace set,when all billboards have the same cost

▲Figure 5.Performances on the geolife trace set,when all billboards have the same cost

Next, we compare the performances of different advertising strategies on the epfl trace set, which are shown in Fig.4.As we can see from Fig.4a, the performance of ASFCC is far better than that of other strategies.In particular,the strategy Random outperforms the strategy ASFCC-Basic when the deadline is set to 550-600, which can prove the limitation of the local optimum of ASFCC-Basic.The similar phenomenon can also be seen in Fig.4b,where the performance of Random is better than that of ASFCC-Basic.We also test the influence of budget and the number of customers’preferences on ASFCC’s performance at the same time and the results are shown in Fig.4d.It is obvious that the performance of ASFCC shows an upward trend when two variables increase, which is also consistent with the performances in Figs.4b and 4c.

In Fig.5, we show the performances of different strategies on geolife traces.We rank the performances of different strategies as follows: ASFCC ＞CG ＞ASFCC-Basic ＞Random.It is reasonable because the instability of the Random leads to poor performance.At the same time, CG and ASFCC-Basic have their limitations, resulting in the final results not as good as ASFCC.Based on the experimental results of the three datasets, we can find that our strategy ASFCC can always achieve the optimal results under different conditions.

Finally,we conduct the simulations to verify the correctness of the approximation ratio for ASFCC.As shown in Table 2,the results of ASFCC when the deadline is from 500 to 550 are obviously larger thanOptimal, which are consistent with our theoretical analysis.

6.4 Simulation Results for Single-Product with Different Billboard Costs

In this part,we conduct the simulations to compare the performance of ASFDC with other two strategies when all billboards have different costs.The results are shown in Figs.6,7 and 8.

First of all, we compare the performances of different advertising strategies on the roma/taxi trace set, and the results are shown in Fig.6.By changing the deadline,we can find that the strategy ASFDC outperforms the other two strategies.Because ASFDC selects the billboards with the consideration of potential customers’preferences, detour distance and the probabilities of seeing the billboards, thus the billboards selected by ASFDC can achieve better commercial profit.Note that it is reasonable that the commercial profit may increase when the budget grows,because the advertiser may select more billboards for advertising so that more potential customers can be attracted.The results in Fig.6b can match our analysis.

Next, we conduct the simulations on the epfl trace set and the results are shown in Fig.7.Obviously,we can find that the ASFDC performs much better than ASFDC-Basic and Random.Because ASFDC-Basic selects the billboards with maximum commercial profit which is a local optimum, the billboards selected by ASFDC-Basic may be seen by a small group of potential customers so that the commercial profit cannot be maximized.We also test the performance difference be-tween ASFDC and Random when the costs of billboards are under different distributions(uniform distribution,poisson distribution and normal distribution),which are shown in Fig.7d.The difference values in Fig.7d are calculated by subtracting the profit of strategy Random from that of strategy ASFDC.The larger the difference value is, the greater the performance gap between these two strategies would be.As we can see from Fig.7d, it is clear that the difference value decreases as the budget increases.When the costs of billboards are under uniform distribution, the difference between ASFDC and Random is the greatest,and when the costs of billboards are under normal distribution, the difference is the smallest.However,this difference is small among the three distributions when the budget is same.Hence, our proposed strategy ASFDC can be adopted when the costs of billboards are under these three distributions.

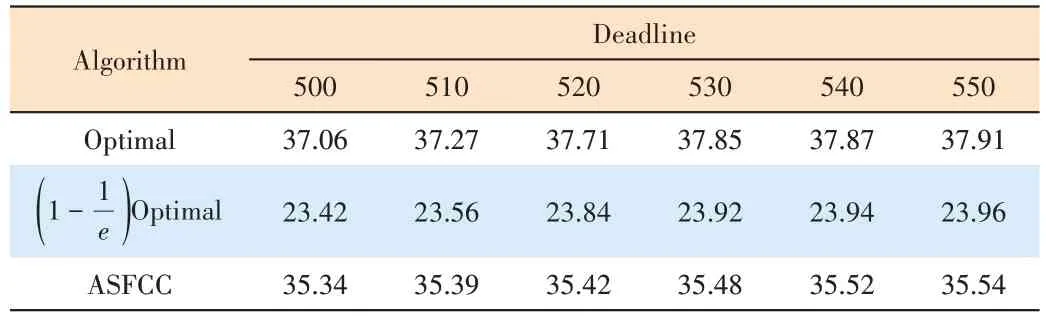
▼Table 2.Simulation results on epfl, when all billboards have the same cost

We then evaluate the performances of three strategies:ASFDC, ASFDC-Basic and Random on the geolife traces,which are shown in Fig.8.We can find that similar phenomenon as that in Figs.6 and 7 also appears in Fig.8, where the performance of ASFDC is much better than other two strategies.The reason for this phenomenon is similar to that in Figs.6 and 7,so it is omitted here.

Finally, we conduct simulations to verify the correctness of the approximation ratio for ASFDC on epfl trace set where the deadline is set from 500 to 550, and the results are shown in Table 3.Compared with the results ofoptimal, we can easily see that the results of ASFDC are larger,which matches the theoretical analysis.

▲Figure 6.Performances on the roma/taxi trace set,when all billboards have different costs

▲Figure 7.Performances on the epfl trace set,when all billboards have different costs

▲Figure 8.Performances on the geolife trace set,when all billboards have different costs

▼Table 3.Simulation results on epfl,when all billboards have different costs

6.5 Simulation Results for Multi-Product

In this part,we conduct the simulations to compare the performance of ASFMDC with other three advertising strategies:ASFDADC, ASFDADC-Basic and Random.The detailed results are shown in Figs.9,10 and 11.

Firstly, as shown in Fig.9, we conduct the simulations on the roma/taxi trace set to compare the performances of different strategies.We can rank the performances of different strategies as follows: ASFMDC ＞ASFDADC ＞ASFDADC-Basic ＞Random, which can prove the effectiveness of our proposed strategy ASFMDC.We can also find that the result of ASFMDC is improved by about 5%-10% compared with ASFDADC,where ASFMDC is based on ASFDADC.The reason is that ASFDADC selects the billboards which can maximize the total expected commercial profit, while ASFMDC conducts a search in different directions based on ASFDADC, selecting the optimal neighbor solution as the final result.Thus, our strategy can improve 5% to 10% compared with ASFDADC,which is reasonable.The performance of Random is much worse than that of the previous two experiments.Because the advertiser needs to select billboards and determines their corresponding advertisements, Random introduces a lot of uncertainties, which makes the result much worse than the other strategies.

▲Figure 9.Performances on the roma/taxi trace set,when the advertiser has multiple products

▲Figure 10.Performances on the epfl trace set,when the advertiser has multiple products

▲Figure 11.Performances on the geolife trace set,when the advertiser has multiple products

Then, we show the results of the simulations on the epfl trace set in Fig.10.ASFMDC can achieve the best commercial profit for the advertiser and the performance of ASFDADC is close to ASFMDC.However,the performances of the above two strategies are far better than ASFDADC-Basic,which is different from the phenomenon in Fig.9.Because the billboards selected by ASFDADC-Basic may achieve a local optimum, when the global optimal solution is very different from the local optimal solution, the result of ASFDADC-Basic would be very bad.In addition, we can find that changing the number of advertisements has a greater impact on the results.This is because a potential customer can be attracted by different products, when the number of advertisements increases,potential customers can be attracted to buy new products and the commercial profit is improved significantly.

Finally, Fig.11 shows the performances of different strategies on the geolife traces.We can find that the phenomenon in Fig.11 is similar to that in Fig.9, where ASFMDC performs better than other three strategies.The performances of ASFDADC and ASFDADC-Basic are close to ASFMDC and much better than that of Random.It is not difficult to find that the results of different strategies increase with the growth of the four variables in Fig.11, which is reasonable.Because the growth of budget and deadline would increase the number of the selected billboards and the probabilities that selected billboards would be seen by the customers.When the number of products and customers’preferences grow,the potential customers who see the advertisements would be more likely to be attracted.From the above figures, we can prove that our advertising strategy ASFMDC can bring more commercial profit to the advertiser,compared with other common strategies.

7 Conclusions

In this paper, a billboard selection problem is formulated in order to maximize the commercial profit for the advertiser under the limited budget.In order to address this problem, first of all, we adopt MCS to collect potential customers’traces and preferences.Then, we use the semi-markov model to predict the customers’mobility patterns.Next, we quantify the utility of each billboard with the consideration of customers’preferences, detour distance and the probabilities of seeing the billboards.Two heuristic advertising strategies are proposed in this paper to determine which billboards to select for the situation where the advertiser has only one type of product.Then, we adopt the simulated annealing algorithm to address this problem when the advertiser has multiple products.We conduct the extensive simulations based on the widelyused real-world trajectories: roma/taxi, epfl, and geolife.The results show that our advertising strategies can bring the best commercial profit for the advertiser compared with other advertising strategies.