数学学习不良中师生的表征特点研究

武晓梅

摘  要：本研究以中师学生为研究对象，以排列组合为内容设计表征测试工具。通过与学习优秀学生对比，揭示学习不良学生的表征特点。结果表明：与学习优秀学生相比，学习不良学生表征方式单一，缺乏多种表征的习惯和能力;在表征方式上更倾向于由抽象向具体的表征;对问题深层表征能力低。

关键词：表征方式;表征顺序;表征深度;数学学习不良中师生

中图分类号：G715          文献标识码：A            文章编号：1672-4437（2021）02-0047-04

学习不良学生是指学习效率低下，智力正常，不能达到学校教学规定的基本要求的学生[1]。近年来中师学生中学习不良学生的比例明显增多，提高其学习能力成为亟待解决的问题。

表征是指信息的记载或表达方式[2]。表征又称心理表征或内在表征，它是外在事物在心理活动中内在的呈现。以往研究发现，学习不良学生与学习优秀学生相比，表征存在差异。那么中师生中数学学习不良者与优秀者存在哪些差异，他们在数学问题解决的表征中表现出哪些特点？这正是本研究要探讨的问题。

一、研究方法

（一）被试

研究的取样来自阜阳市某专科学校中师小教专业二年级的1-6个班的学生。按照标准选出学习优秀的学生69人，学习不良的学生69人。分为6个小组，每组23人。

（二）实验材料

本研究所用的测验是数学问题表征和数学问题解决测试。本问卷选用的是开放式的数学问题，共有3道题目组成，测验的内容主要涉及排列组合（这部分知识学生在测验前一学期学完）。

试题1：甲、乙、丙、丁四名同学和一名老师站成一排合影留念，不同的站法有多少种？

试题2：甲、乙、丙、丁四名同学和一名老师站成一排合影留念，要求老师必须站中间，不同的站法有多少种？

试题3：甲、乙、丙、丁四名同学和一名老师站成一排合影留念，要求老师必须站中间，甲同学不与老师相邻，不同的站法有多少种？

（三）实验设计与程序

本测验主要从三方面研究数学学习不良学生的表征特点：第一，学习不良学生表征方式是单一还是多样;第二，在多种表征方式中是由具体到抽象，还是由抽象到具体;第三，和学习优秀学生相比，其表征深度有无差异。

测验在2018年3月进行，由6名数学教师做主试（他们不知道测验的具体目的），同时在6个班进行测试。测试时间分别为60分钟。要求被试完成试题，并写出具思考过程，标注思考时间。

二、结果与分析

（一）两类学生使用多种表征频数的差异比较

在测验题作答中，被试成功使用图形和公式表征两种方式解答即为多种表征，如只成功使用一种表征方式为单一表征。纪桂萍等把数学问题解决中的心理表征分为形象表征和抽象表征两种[3]。形象表征是以图片、图形的形式进行呈现。形象表征比较生动、形象，而且它与视觉的关联性也比较强，因此也将它叫做图形表征。抽象表征是以语言、文字和符號、命题、图式等形式存在的表征。表1中，学习不良学生使用多种表征的频数为0.89±0.69，学习优秀学生使用多种表征频数为2.09±0.85，对两者多种表征使用频数的差异比较，t=-7.94（P=0.000<0.001）。结果显示，被试在测验题中选择多种表征频次存在差异。学习不良学生和学习优秀学生在问题解决过程中使用多种表征的频数存在显著差异，优秀学生更多使用多种表征方式。

学习不良学生更多使用单一的表征方式，对问题的理解往往不够全面、深刻。事实上，具体的数学问题往往包含有多种信息，一种表征方式，往往只能获得部分信息而非全部，信息遗漏会影响对问题的准确理解，甚至是造成对问题的错误判断，使问题解决失败，这一观点已被诸多研究证实。学习优秀的学生，更倾向于选择多种表征结合的方式。多种表征可以理解为将语言、文字、符号、图片、具体物、活动或实际情景等多种形式相结合的综合表征形式。借助不同的表征形式，形成对问题的不同属性和特征的认识，获得多方面的信息。Keller认为，数学的多种表征形式能够形象具体的凸显数学学习对象的两个方面：一是数学学习对象的多元属性可以强化其复杂性，能够便于学生对不同表征进行转换;二是它的多元属性也可以淡化其复杂性，能够便于学生对不同表征的认识联结[4]。因此，缺乏多种表征结合习惯和能力，是导致学习不良的原因之一。

（二）两类学生表征的顺序比较

分析学生的思考过程和解题过程发现，两类被试选择表征顺序和解题思路存在差异。无论学习优秀的学生还是学习不良的学生都试图通过多种表征方式去寻找不同的解决思路。从表2可以看出，两类学生在两种表征方式使用的先后顺序上存在差异：第1题，学习优秀学生中52人成功解题，，其中41人使用具体到抽象表征，11人使用抽象到具体图形表征;学习不良学生中29人成功解题，其中10人使用具体到抽象表征，19人使用抽象到具体图形表征。第2题，学习优秀学生中47人成功解题，其中38人使用具体到抽象表征，9人使用抽象到具体图形表征;学习不良学生中17人成功解题，其中6人使用具体到抽象表征，11人使用抽象到具体图形表征。第3题，学习优秀学生中47人成功解题，其中37人使用具体到抽象表征，10人使用抽象到具体图形表征;学习不良学生中16人成功解题，其中4人使用具体到抽象表征，12人使用抽象到具体图形表征。卡方分析结果分别为15.71、10.90、17.84，P分别为0.000<0.01、0.002<0.01、P=0.000<0.01。结果表明，学习优秀的学生更倾向于具体图形—抽象表征，而学习不良者更愿意从抽象到具体图形表征。

长期以来的争论专注于使用具体表征还是抽象表征，特别是，数学和科学。尽管具体到抽象应该是一个连续体，人们通常很极端，把具体和抽象对立起来。Bruner于1966年最先提出CRA技术，允许学习者开始有益于具体情境，鼓励他们超越具体情境，逐渐去除无关的细节，抽象概括它们[5]。Fyfe[6]、Ching B.H.-H.， Wu X研究发现，具体到抽象的表征顺序是成功学习的关键[7]。思维的发展是从具体到抽象的，知识的学习也是由感性上升到理性的。因此，学生在认识事物或问题解决中，也应遵循从具体图形到抽象表征的过程。具体表征形式具有外显性、展开性和直观具体性。首先进行直接观察，容易理解具体物体、实际情境，激活现实世界的知识。其次具体表征既具有具体性，又具有形象性，更有利于学生从感性上升到抽象概念，形成知识之间本质、内在联系，它可以帮助学习者理解模糊且复杂的抽象概念。因此，如果具体材料先于抽象材料，学习者可以用已经理解的具体材料或情境来解释意义模糊的抽象材料。而学习不良者更多选择从抽象到具体的表征，抽象材料会使得学习者在没有被理解的情况下，操纵无意义的符号[8]。研究发现以抽象的形式解决问题经常导致无效的解答策略[9]，习得程序的不灵活的运用[10]，或出现非逻辑错误[11]。

因此，问题解决中由抽象到具体的顺序，导致学生没能充分理解问题。直接使用抽象表征形式，是学习不良者解题失败的重要原因之一

（三）两类学生表征深度比较

辛自强教授提出了“表征复杂性模型”，以此来考察或区分儿童的表征能力。他认为数学问题，特别是数学应用题最本质的属性往往是题目所涉及数量或集合关系的复杂性。以最基本的算术应用题为例，一般只涉及三个集合，其中两个集合已知，求第三个。在这些问题中，三个集合存在一定的关系（比如部分-整体关系），我们称之为集合之间的初级关系。如果集合的集合又与别的集合发生了关系，那就是建立在初级关系基础上的二级关系，依次类推，可以有三级关系、四级关系等。这种由关系的层级数决定的问题的复杂性，可以称为关系的等级复杂性，而对问题表征的质量主要取决于能理解的关系的最高层次，即表征深度。

本实验材料为排列组合题，试题1，只涉及排列问题，其解决过程为五人排，即P（5，5），列式正确得6分，其表征深度为初级关系;试题2中，要先将老师选出站中间，在將其他四人排列，即C（1，1）P（4，4），每个关系正确得3分，共6分，其表征深度为二级关系;试题3在选出老师站中间后，再将甲同学排在两边，最后排列其他三人，每个关系正确的2分，共6分，即C（1，1）C（2，1）P（3，3），其表征深度为三级关系。

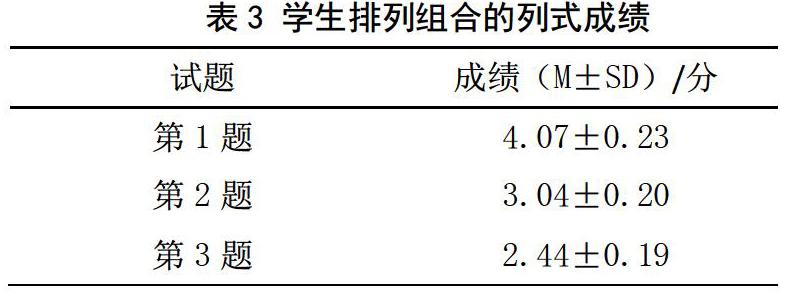
分析所有被试对三类题目的重复测量的方差表明（见表3），在排列组合计算测验上三道试题之间存在极为显著的主效应，F=488.80， p=0.000<0. 001。前后两个试题结果配对T检验表明，两个试题之间的正确率均有极其显著的差异t1-2= 4.12， p=0.000<0.001;t2-3=2.70，p=0.000<0.001。这说明，在三道试题的计算方面，存在明确的难度等级。

在表4中，对学习优秀（69人）和学习不良（69人）两类学生的成绩做了比较，结果表明，无论就各个试题而言，还是就整个测验而言，两类学生的成绩都存在显著差异。事后比较表明，学习不良学生的排列组合计算成绩通常落后于优秀生。第1题，学习优秀学生成绩为4.87±0.32分，学习不良学生成绩为3.26±0.32分;第2题，学习优秀学生成绩为4.30±0.28分，学习不良学生成绩为1.78±0.28分;第3题，学习优秀学生成绩为3.93±0.27分，学习不良学生成绩为0.96±0.28分。方差分析结果显示，两类学生在三道试题存在显著差异。由此可以看出，优秀生通常有较高的图式水平，表征深度通常较大，理解表征问题中复杂关系的能力较好;而学习不良学生的图式水平相对较低，不善于理解表征问题中复杂的关系。从表4可以看出，两类学生三题的得分差值分别为1.61、2.52、2.97，随着试题层次的升高，两类学生得分的差距也越来越大。

三、结论与建议

本研究对数学学习不良的中师学生进行表征特点分析。通过测试了解学生对数学问题表征的选择倾向及其对问题解决的效果的影响。研究发现，学习不良学生问题表征具有以下三方面特点：一是表征方式单一，缺乏多种表征的习惯和能力。因此，教师在日常教学中要改变传统教学只关注抽象表征的方式。根据教学内容和学生的特点，适时将形象表征、抽象表征等多种表征结合。同时注意把握每个层面的知识点及知识点的整合。使得各种表征方式所提供的信息不是孤立的、分散的存在，而是能看到不同表征所提供信息的统一性。

二是在表征问题时，多倾向具体到抽象的方式。以往表征研究中往往只考察是否使用多种表征，很少研究不同表征顺序对学习者的影响。研究发现，对学习不良学生来说，不经具体表征过程直接使用抽象表征，容易让学生死背公式，或生搬硬套某类熟悉的题目。布鲁纳在1966年提出，外在刺激程度深刻影响着学生思维活动的水平。他用动作的、形象的和符号的三种表征来代表不同的外在刺激程度。并且认为，学生的思维水平是以“线性”或“单向性”的方式从动作表征到图形表征，最后再到符号表征。实物表征能够更直观地感受数学对象，形象表征能够直观地传达大量数学图形信息，在具体表征基础上再进行深度表征，更有利于提高学生解决问题的能力。三是深层表征问题的能力低。以辛自强的关系-表征复杂性模型（RRCM）为基础确定问题的难度序列，该模型能够有效解释问题（解决）难度的本质，实验结果也证明了两类学生在表征的深度上存在显著性差异。因此，针对学习不良学生，对教学材料的确定，对考试问题难度的排列无疑都应考虑表征深度的问题。教学中教师可以把某个领域的各种问题按照由易到难的顺序组织起来，使教学或练习真正做到“循序渐进”。对于学习不良学生，学习表征低级关系是重点，应该帮助他们建立基本的图式并学会使用基本公式，促进其表征深度，提高其图式水平与知识基础。

參考文献：

[1]吴增强，段蕙芬，沈之菲，等.学业不良学生类型与特点的聚类分析[J].心理学报，1994（01）：92-100.

[2]荆其诚.简明心理学百科全书[M].长沙：湖南教育出版社，1991.

[3]纪桂萍，焦书兰，何海东.小学生数学问题解决与心理表征[J].心理发展与教育，1996（01）：29-32.

[4]Keller&Hirsch.Students preferences for representations of functions. International Journal of mathematics[J].

Education in Science and Techonology，1998（29）：1-17.

[5]Bruner，J.S..Toward a theory of instruction[M]. Cambridge： Harvard University Press，1966.

[6]Emily R. Fyfe，Nicole M. McNeil，Ji Y. Son，Robert L. Goldstone. Concreteness Fading in Mathematics and Science Instruction： a Systematic Review[J]. Educational Psychology ，2014（26）：9-25.

[7]Ching B.H.-H.， Wu X. Concreteness fading fosters children's understanding of the inversion concept in addition and subtraction[J].Learning and Instruction， 2019（61）：148-159.

[8]Nathan， M. J. Rethinking formalisms in formal education[J].？Educational Psychologist， 2012，47（2）：

125-148.

[9]Koedinger， K. R.， & Nathan， M. J. The real story behind story problems： effects of representations on quantitative reasoning[J].？Journal of the Learning Sciences， 2004（13）：129–164.

[10]McNeil， N. M.， & Alibali， M. W. Why wont you change your mind？ Knowledge of operational patterns hinders learning and performance on equations[J].Child Development，2005，76（4）：883–899.

[11]Carraher， T. N.， & Schliemann， A.D. Computation routines prescribed by schools： help or hindrance[J].？Journal for Research in Mathematics Education， 1985（16）： 37-44.