生成对抗网络在风电功率预测中的应用
陈 刚,王 印,单锦宁,李天奇,郑雯泽,王 雷,苏梦梦,黄博南
(1.国网辽宁省电力有限公司 阜新供电公司,辽宁 阜新 123000;2.国网辽宁省电力有限公司 电力调度控制中心,辽宁 沈阳 110006;3.东北大学 信息科学与工程学院,辽宁 沈阳 110819)
0 引言
随着环境污染、资源减少和全球变暖等问题的日益恶化,作为优化能源结构的重要手段之一的清洁能源的不仅提高能源安全,而且是中国能源发展战略目标[1-3].风能是许多国家用来替代传统发电、减少温室气体排放的重要清洁能源.随着风能的快速发展,由于风电的波动性、不确定性,风电机组渗透率不断增加对电力系统的运行产生了影响.风电预测是应对大规模风电一体化给电力系统带来挑战的重要手段之一,风电功率预测的精度直接影响风力发电并网运行的可靠性.因此,近些年来众多研究学者针对风电预测提出很多研究成果,并且在实际应用中卓有成效.
现有的风电功率预测方法主要分为:物理学方法和统计学方法.物理预测方法是将天气实时状态和典型风机中的可变参数作为变量建立数学模型并预测风电功率.统计方法是基于统计学手段采用实测数据得出风电功率典型曲线.物理学预测方法主要有持续预测方法[4]、卡尔曼滤波法[5-6]、随机时间序列法[7]和人工神经网络法[8-9]等单一算法以及一些组合预测方法.现阶段许多风电功率预测方法只是针对正常情况下数据进行建模,没有考虑异常情况下的风电数据.由于异常情况很少发生,且在数据预处理时对异常数据进行修正,使得预测模型只能预测正常情况下风电数据,忽略异常数据.许多国内外学者在风电功率预数据预处理时对异常数据进行识别和清洗从而修正为正常情况下的数据.许多风电预测研究对数据处理采用查表的方式[10-11],这些研究通过判断预测数据是否超出一定的临界值从而实现对异常数据的识别,而不考虑数据序列的序列特征.文献[12]由于采用四分位法剔除离群散点,结合聚类算法识别堆积型的数据,识别异常数据时造成误识别大量正常数据,识别精读较低.文献[13]由于通过分段求取组内最优方差,识别异常数据,造成上部异常数据无法识别,其方法不具有普遍性.文献[14]对异常数据进行识别时采用参数化公式条件准则,由于每次使用需重新设置参数,造成此方法实用性不强.以上方法通过概率统计分析异常数据,同样使得正常数据被误识别.另外,由于现场情况的复杂性,有时很难确定正确的边界,容易导致判断错误.其他一些研究考虑用统计方法处理异常情况下风电数据,尤其是由负荷预测的数据验证技术扩展而来的小波奇异性检测方法.但小波奇异检测法受日负荷曲线的周期性特征和类似负荷日的影响较为严重.因此,小波奇异检测的数据处理方法不太合适风力发电的情况.况且,风电功率曲线中的一些异常数据可以用负荷曲线与不规则因素之间的因果关系来解释.
基于以上的分析,本文提出一种基于生成对抗式网络的风电功率预测算法.该算法首先利用联合分布KL散度代替传统的条件分布KL散度,进而确定正常数据与异常数据间的联系与边界;然后,通过微调更好地学习历史和未来数据之间的精确条件分布;最后,利用生成器网络对抗训练方式实现风电功率预测.通过辽宁省某风电场的风电功率数据对本文所提算法进行了仿真验证,结果表明本文所提算法不仅可以减少数据清洗,而且实现风电功率的快速准确预测.
1 传统的预测方法
1.1 传统风力发电预测方法
传统风力发电预测方法的核心是适当地建立一种特殊的可学习的映射关系,该关系将历史记录(包括风力发电数据和天气状况)和未来风力发电数据联系起来.本文使用符号S来表示时间步长t处的风力发电功率,因此:N代表N+1个历史记录的序列(s0,s1,… ,sN).此外,为简单起见,使用S0:t−1表示St前有固定长度的历史记录.
预测问题通过从概率的角度来看.视时间步长t的风力发电功率为随机变量,取决于历史数据,其条件概率p(st|s0:t−1)服从一定的分布.通过概率推理方法用来找到这种未知的分布.传统的方法是建立一个可学习的模型q(st|s0:t−1)由一个或一些参数θ控制,然后最小化可学习模型q(st|s0:t−1;θ)和真实条件分布p(st|s0:t−1).
两个分布之间的差异通常由库尔巴克-莱布勒(KL)散度测量为
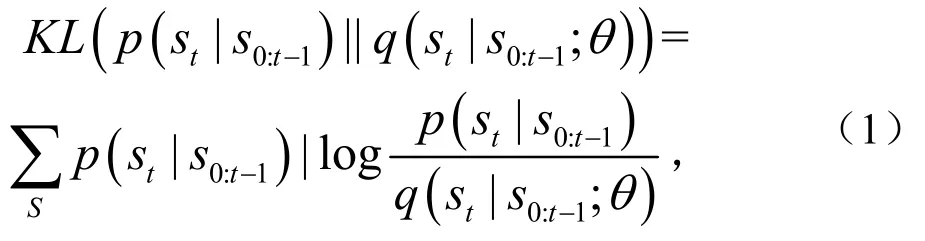
式中,S为sr的所有可能值的集合.
使用库尔巴克-莱布勒散度,最佳参数应满足
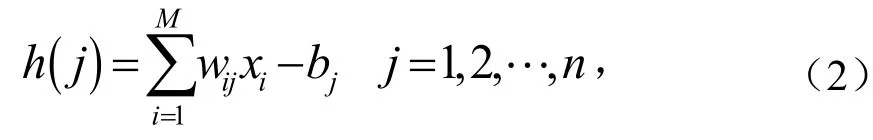
然后基于梯度的优化方法来计算θ*.
本文用S来表示由条件参数模型给出的预测风力发电功率.若模型已经被拟合到训练数据,预测S就可以以随机确定的方式从条件分布中得出
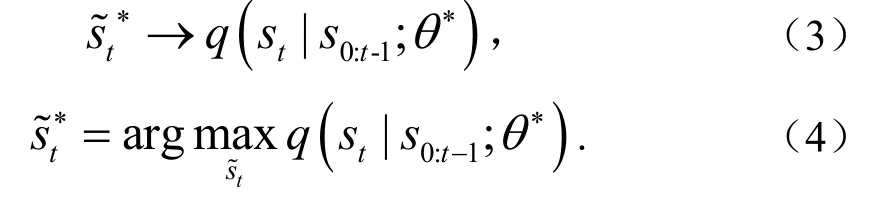
采用复杂模型,例如深度神经网络作为参数模型q(st|s0:t−1),传统预测方法一般可以达到较高的精度.
1.2 风力发电系统中的突发事件
常见数据和异常数据之间的关系为
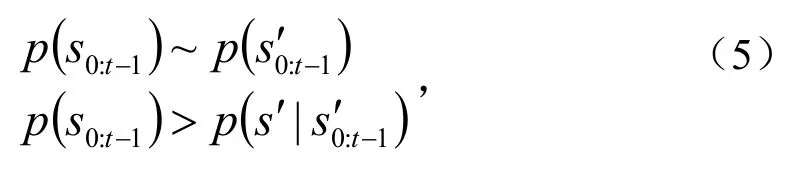
传统的风力发电的方法忽略异常值,以防止过度拟合.传统方法根据正态分布理论,当控制图中存在数据点超出控制界限时,就可判断风力发电机处于异常状态.为了提高数据异常检测的准确率,传统方法将异常模式分为3类,即越界模式、屡临界模式、渐变模式.
越界模式的公式为
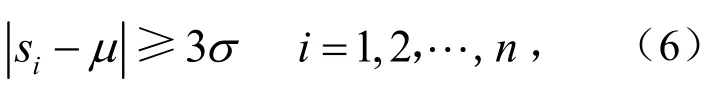
式中,Si为第i个样本的均值,可以在系统数据库中直接读取;μ和σ分别为功率分布中心和标准差,由样本计算求出.
屡临界模式(接连3个点中有至少2个点临近控制限)
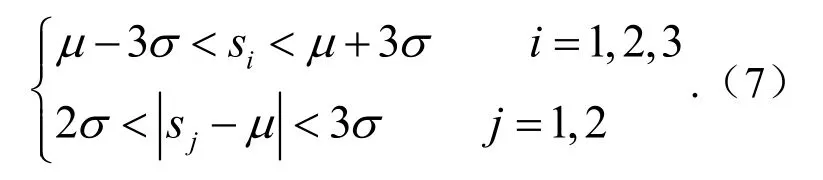
集结中心模式(接连 15个点在中心线附近呈现集中状态)
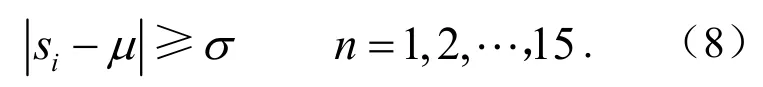
链状模式(接连7个点处于中心线一侧)为
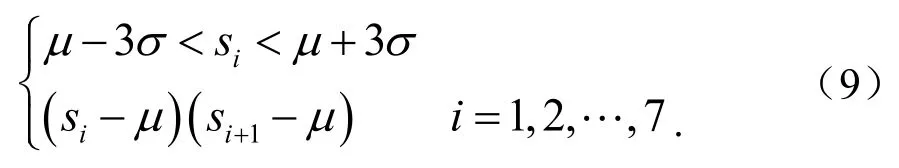
根据上述异常模式规定,本文所采集的数据只有2%满足异常数据.上述方法仅从概率统计角度分析异常数据的特征,会造成大量正常数据被误识别.另外,由于现场情况的复杂性,有时很难确定正确的边界,容易导致判断错误.判断错误会导致预测失误,而预测失误可能会导致风力发电不稳定或经济收益降低,这意味着风力功率的错误模型.此外,功率曲线中的异常数据可以用功率曲线与不规则因素之间的因果关系来解释.因此,风力发电预测迫切需要对极端情况进行准确预测.
本文定义的异常情况是在异常天气状况下仍然满足功率曲线与不规则因素之间的因果关系.
2 模式敏感网络
2.1 模式敏感预测
传统数据驱动的方法被设计成忽略异常的模式.为让模型更加关注异常模式,采用的解决方案是使用联合分布的 KL散度代替条件分布.两个分布之间的差异通常由库尔巴克-莱布勒(KL)散度表示为
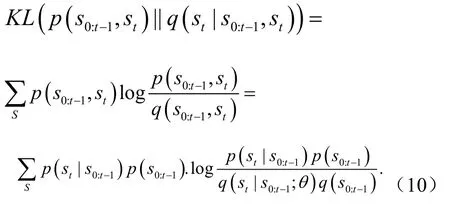
注意,p(s0:t-1)不依赖于p(st)和p(s0:t-1,st).

由于p(s0:t-1)∈[0,1],当接近于0,且q接近p时,可以得到
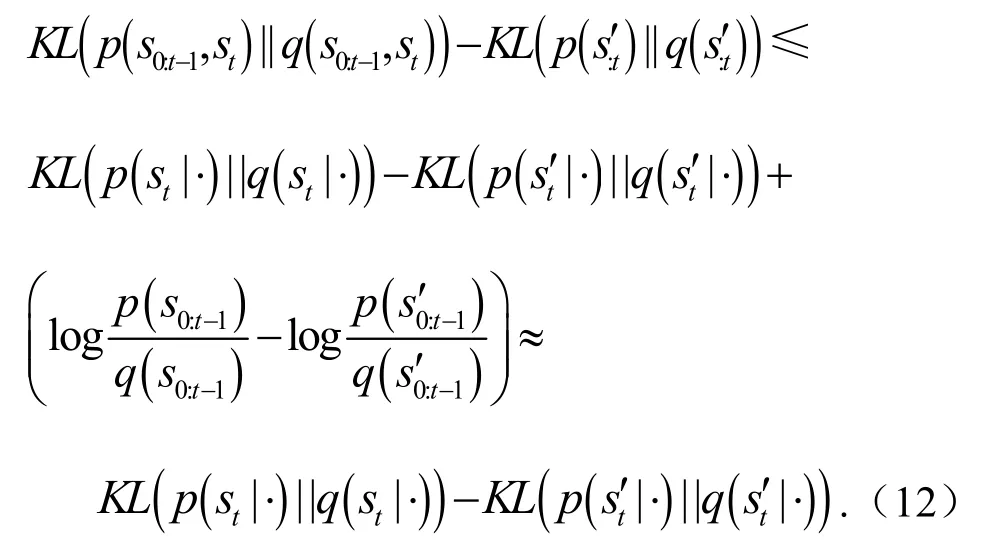
式(12)表明,通过学习联合分布而不是条件分布,可以缩小不同情况下KL散度之间的差距,使模型更加关注异常模式.由于这种预测方法对不同的模式更加敏感,称之为模式敏感预测(Pattern-Sensitive Prediction,PSP).
2.2 模式敏感网络
对于风力发电预测问题,深度神经网络具有比传统的模型更高的拟合的能力.此外,其灵活性允许进行多模态数据融合,进一步提高了其性能.
传统的神经网络通常被建模为条件分布,不是联合分布.由于传统的神经网络执行确定性映射过程,因此必须有输入才能获得相应的输出.最近发展起来的一种称为生成对抗网络的方法就是一个例外.GAN属于隐式密度模型,可以在通过从数据分布中采样来间接与数据分布交互的同时进行训练.
生成对抗网络(Generating Adversarial Networks,GAN)的基本思想是在两个神经网络(发生器和判别器)之间建立一个对手博弈.发生器将噪声源z~p(z)映射到输入空间.判别器接收生成的样本或真实的数据样本,并试图区分它们.使得这种竞争会收敛到一个平衡,同时生成器样本与鉴别器无法区分.这表明生成器是真实样本分布的近似值.通过生成对抗网络引入预测模型,能够使用神经网络进行模式敏感预测.通过将生成对抗网络的对抗结构和辅助损耗相结合,提出了一种新的结构(模式敏感网络).这个模型可以首先推断历史记录,因此,未来状态会自动发现异常模式,并通过提供不同的表示将数据分类到不同类别中.根据从上一阶段学到的表示可以用于更好的预测.这个网络的结构见图1.
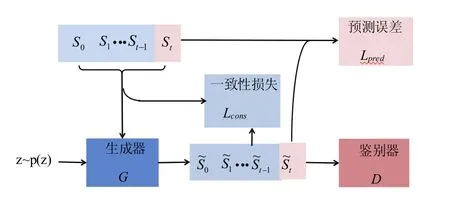
图1 PSN的原理Fig.1 schematic of PSN
图2为PSN网络结构.由如图2可知,PSN的主要组成部分是两个对手网络,其中一个发生器接收随机噪声和历史记录,生成器输出一系列值并根据3个标准进行优化.
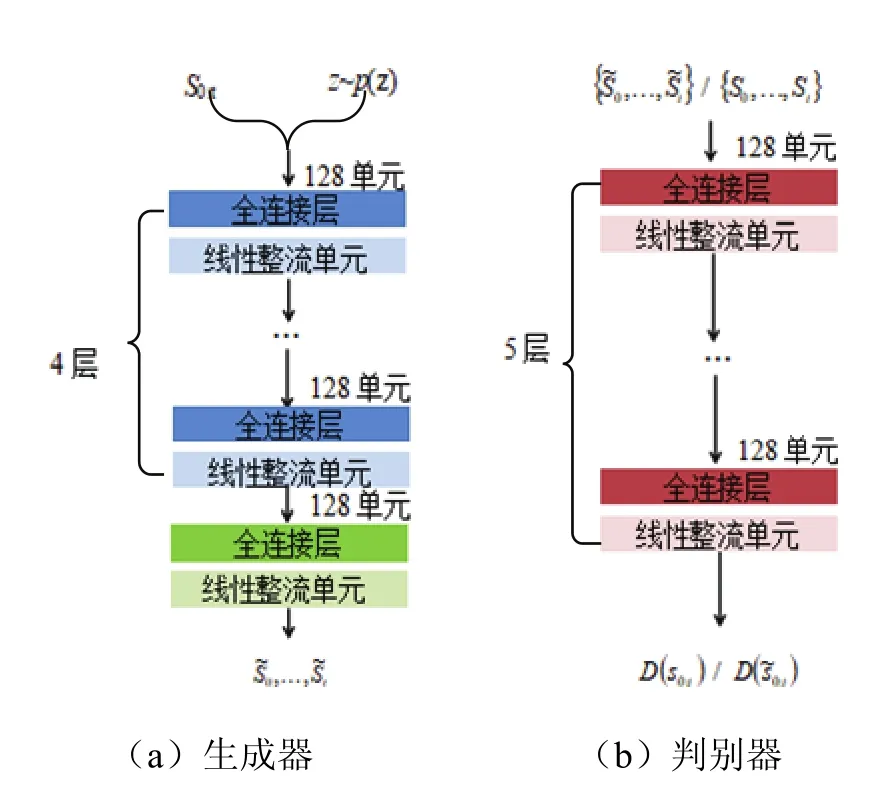
图2 PSN网络结构Fig.2 PSN network structure
首先是鉴别标准D(G(z ,s0:t−1)),它由鉴别器提供以指示生成序列是否可以从真实序列中分辨出来.一致性损失系数用于减少历史记录的重建误差,即最后一个标准是预测误差Lpred,用于衡量预测精度.生成器的总目标函数可以形成为
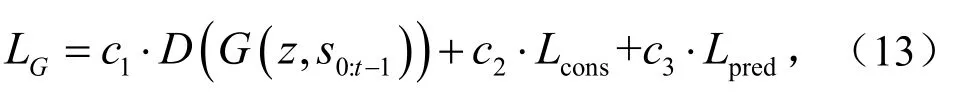
式中,ci为不同损耗的系数.
2.3 PSN的应用
本文实现了一个模式敏感网络来预测沈阳主要风力发电功率预测.仿真采用一种具有梯度惩罚的生成对抗网络(WGAN-GP),其中包含具有权重θ的生成器G和具有权重ω的鉴别器D.与原始生成对抗网络相比,这种代替詹森-香农发散.
由图2(b)可知,鉴别器接收或一般采样,然后输出鉴别结果.鉴别器的目标是最大化D(s0:r)和D()之间的预测误差.为保证鉴别器是最佳的,梯度惩罚也适用于随机混合真实的生成样本ˆ为
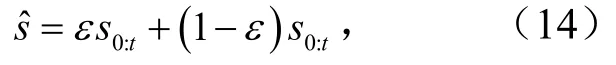
式中,ε为随机变量,从0到1均匀采样.
鉴别器的目标函数定义为
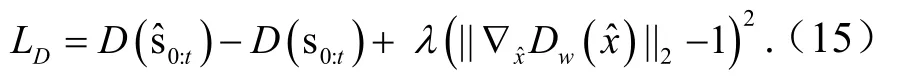
生成器的目标函数有3个部分,如前一节中的式(13).本文将预测误差和一致性损失定义为均方误差.因此,生成器的目标函数定义为
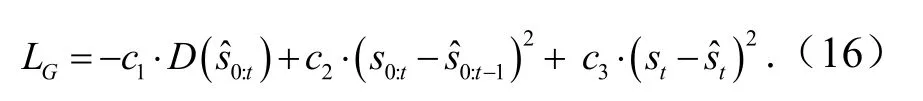
PSN的第一个训练阶段是一个无监督的预处理过程,对从不同站点收集的混合数据集执行.因此S0,S1,… ,SN序列号.学习过程遵循文献[12]中介绍的方法,其中鉴别器将针对N时期进行训练,而生成器仅针对一个时期.通过不同风力发电机组上获得的数据集进行对抗训练,生成器可以拟合风电功率生成器的联合分布.
然后,从无监督阶段获得的数据可用于执行监督任务,因此生成器不会看到训练数据,过拟合的风险更低.最直接的方法是根据预测误差优化生成器.该过程对给定记录的条件分布进行了更好地估计,并提高了模型对特定区域的预测精度.发生器和鉴别器都是通过堆叠5个完全连接的层和128个单元来构建的,每个层都遵循整流线性单元(Rectified Linear Unit,ReLU).生成器中的最后一层在整个训练过程中始终被训练,而其他层只能在无监督学习阶段进行训练.这个实行过程见图2.
3 算例
本文在 TensorFlow 深度学习框架下采用深度GAN网络进行训练, 采用NVDIA GTX 1080 Ti GPU和 IntelCore i7-7700 CPU 作为硬件平台.
3.1 数据描述
(1)输入量的选取
由于过多的预测因素不仅导致模型计算量增大,而且模型导致泛化能力的降低,但是过少的预测因素可能会导致预测信息缺失,从而使得模型无法对所收集数据进行全面分析;所以在风电功率预测前采用合适的输入量非常必要.
由于风电功率和空气密度的关系式为

式中,Cp为风能利用系数;Pw为风电功率,kW;ρ为空气密度,kg/m3;M为风机卷叶的面积,m2;v为当时风速值,m/s.
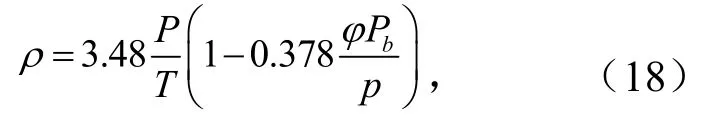
式中,P为正常大气压,取值为 101.325 kPa;Pb为饱和蒸汽压,kPa;T为热力学温度,℃;K为相对空气湿度值.
由上式可知,风电功率与现场风速、温度、湿度、压力密切相关,由于存在一定的相关关系,因此选用这4个影响因素为预测因素.
本文采用的样本数据来自实际辽宁省实际某一风电场风电机组采集的数据的作为实验样本数据集,其中采样开始时间为2015年4月6日13时25分,数据共1 200 000组,每15 min记录1次.预测因素选用现场温度、湿度、风机转速、风速、风向、大气压力等.
(2)数据归一化
由于本文采用多种预测因素的量纲不同,数值差别大,根据本模型采用的激活函数的输入输出范围,将预测因素进行归一化处理,归一化范围为[0,1].
采用最小最大值标准化(Min Max Scaler)进行归一化,计算公式为

由于风电功率实际数据值在 MAPE 指标中作为评价指标的分母,当待预测功率值即为最小功率或与最小功率接近时,使用式(19)预处理导致归一化后的值在0值附近,可能会造成MAPE于无穷大.所以为保证MAPE稳定,本文采用
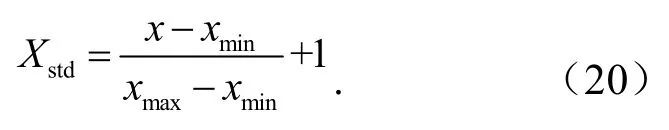
对预测得到的风电功率进行反归一化处理使其具有物理意义,反归一化的计算公式为
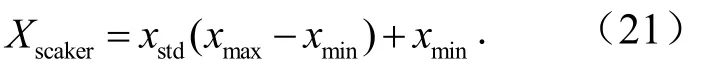
3.2 仿真评价指标
选取平均绝对百分误差 (Mean Absolute Percentage Error,MAPE)以及均方根误差(Root Mean Squared Error,RMSE)作为评判方法优劣的依据,其中平均绝对误差为
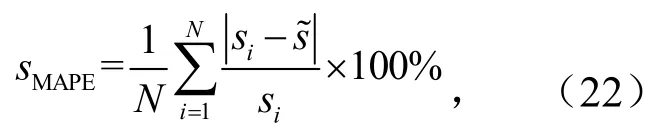
式中,Si为第i个采样点的实际风电功率;为预测功率值;N为样本个数.
均方根误差为
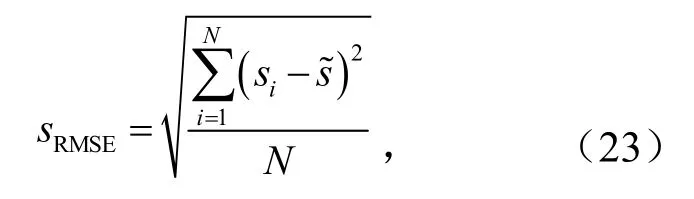
风电功率预测中,实验评判指标越小,则风电功率预测越精确.
3.3 仿真结果分析
(1)激活函数的选择
本模型设置损失函数为均方误差(MSE),通过采用稀疏激活函数 ReLU函数作为模型激活函数和传统的 sigmoid激活函数作为神经网络激活函数进行对比训练.图3为训练集和测试集精度在训练过程中的变化,验证误差、训练误差如图3虚线所示.由图3可得采用ReLU激活函数作为激活函数的神经网络训练性能得到了优化,其评价指标均方根误差从 14.1%降低到了 13.7%.由图3可知采用 ReLU激活函数作为模型的激活函数具有较好的收敛特性.
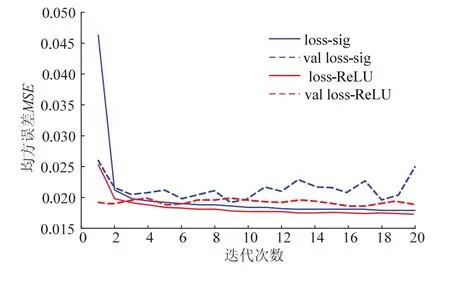
图3 激活函数比较Fig.3 activation function comparison
(2)模型对比
为检验基于生成对抗网络的风电功率预测模型性能,本文采用本文提出的PSP模型与传统的LSTM神经网络模型进行对比.采用风电功率作为模型比较对象,风电功率预测曲线见图4,PSP模型预测的风电功率明显比 LSTM 模型预测的功率更接近实际风电功率.PSP模型和LSTM模型的平均绝对误差MAPE和均方根误差RMSE见表1.RMSE和MAPE比 LSTM模型分别降低了0.64%和0.33%.
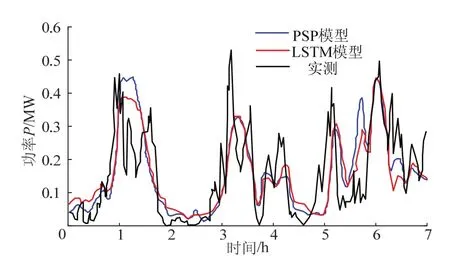
图4 PSP与LSTM 模型预测结果比较Fig.4 comparison of prediction results between PSP and LSTM model

表1 只考虑正常情况下风电功率预测误差评价指标Tab.1 only consider evaluation index of wind power prediction error under normal conditions
同时都考虑异常情况的风电功率情况下,PSP模型和LSTM模型的平均绝对误差MAPE和均方根误差RMSE见表2.RMSE和MAPE比 LSTM模型分别降低了1.05%和0.71%,与只考虑正常情况下的风电功率预测相比,PSP考虑异常情况的风电功率预测均方误差和平均绝对误差均有所降低,而LSTM考虑异常情况的风电功率预测的均方误差和平均绝对误差升高.仿真结果证明基于生成对抗网络的风电功率预测模型的有效性.

表2 考虑异常情况下风电功率预测误差评价指标Tab.2 evaluation index of wind power prediction error under abnormal conditions
4 结论
(1)提出一种基于机器学习理论的风电功率短期预测方法.其中模式敏感网络能够更好地适应风力发电的不同天气条件下的变化模式,从而在极端天气条件下进行更好的预测.测试结果表明,通过让神经网络明确地学习未来数据和历史记录的联合分布,不仅可以更强有力地处理风力发电系统的剧烈变化,而且影响其预测精度.此方法还通过减少对复杂结构的需求减少时间成本.
(2)如果数据比较复杂,可以通过使用更复杂的网络结构来进一步改善PSN.此外,实验证明,采用生成对抗网络的最新发展可以扩展风力发电预测模型的研究.希望通过进一步的应用,能够针对各种条件下风电功率进行更精确的预测,提升预测结果,以及提高的风力发电系统数据恢复准确率.

