基于ANSYS Workbench的电机轴系模态分析

高丰，王福忠，韩素敏

基于ANSYS Workbench的电机轴系模态分析

高丰，王福忠，韩素敏

（河南理工大学 电气工程与自动化学院，河南 焦作 454000）

提升机电机轴的主要作用是将电机的输出动力通过链传动传递至滚筒，为滚筒作业提供动力。不仅要符合强度、刚度等力学条件, 还需要满足一定的动态性能要求。本文针对7800 kW同步电机主轴，通过软件SolidWorks进行建模，并利用ANSYS对其进行有限元模态分析和谐响应分析，得到了该轴前8阶模态的固有频率、振型及扭转角度分布，分析结果可以作为电机轴优化设计的参考, 通过合理的优化也避免在运行过程中与激励频率发生共振，有利于提高电机轴的可靠性与寿命。

电机轴系；有限元建模；模态分析；谐响应分析

提升机在作业过程中的载荷增加数倍，加上频繁的启停使得同步电机轴系振动的危害程度日益加剧，轴系振动问题已成为大型同步电机运行研究的重中之重的[1-2]。其中轴系振动特性研究的基础就是轴系自身的固有特性计算，包括固有频率和振动振型，否则，当电机运行时与其固有频率会产生共振导致轴系发生各种故障，严重的甚至会发生断裂，不仅会使电机无法工作造成经济损失，甚至会影响提升机的安全性造成人身安全问题[3-5]。

轴系扭振动力学分析理论发展较为成熟，多采用集中模型和连续质量模型法[6-8]，周生通等[9]为有效地模拟传动轴系的扭转振动特性建立了集总参数模型，陈星等[10]对同步电机转子系统建立双质量模型，证明了转子系统扭振的稳定性并确定了它的稳态解。付强等[11]在考虑阻尼作用下用整体传递矩阵法计算转子的固有特性。Zhu Z Q等[12]在对同步电机轴系的扭振特性分析时采用连续质量法和相应的传递矩阵。但集中质量和连续质量模型简化了轴系关键部件的柔性，忽略了关键部件对轴系扭振特性的影响。针对这种情况，有限元建模可以精确地反映同步电机系统轴系的复杂时变扭转振动特性，而不受参数设置的限制。黄晓刚等[13]对轴系的扭转振动固有频率进行使用有限元法为用有限元方法分析轴系的扭振提供了依据。任正义、王超等[14-15]采用有限元法精确的计算出了轴系的每阶固有频率并对其模态进行分析。

通过以上分析，本文提出对同步电机系统轴系进行牛振特性分析是采用有限元。首先根据同步电机实际参数建立电机轴系有限元模型，其次对通过有限元模态分析得出各阶模态并对其进行振动特性分析，最后对其进行谐响应分析，通过加载外界载荷查看轴系振动的幅值。通过得到的结果可以使同步电机在工作的是时候更好地避开固有频率减少故障发生，同时也为将来电机的更好的设计提供了准确的理论参考。

1 有限元法的基本理论

有限元法的就是把连续变换状态的整体结构进行离散划分成多个细小的单元，然后通过求解每个单元的应变场和应力场的计算得出整个结构的变量。有限元法具体计算的步骤如下：

（1）整体机构的离散化

结构离散化的目的是将连续变化状态的整体结构分离为多个通过节点相接的单元。为了求出整体结构的解，可以先求解每个单元的解，然后再把其组合起来就可以了。

（2）求解单元位移函数

单元内部移动分布规则的函数用单元的节点值在单元内部定义的位移函数进行模拟，各单元可以再利用相同的共同的位移函数，即：

（3）求出单元应力和应变列向量

由节点的位移分布函数和单元的应变可以求出单元应变列向量：

由上面求出每个单元的应变列向量，通过物理方程可以求出每个单元的应力列向量：

为单元的弹性矩阵，Pa。

通过式（1）可以计算出每个单元的节点力矩阵，同时把每个单元的刚度矩阵导出如下：

（4）总体方程的计算

整体结构的总体方程就是将每个单元刚度矩阵和节点列向量组合起来，将每个节点列向量组合成整体的列向量，最终形成总体平衡方程为：

（5）求解单元的应变和应力

将设置好的边界条件和载荷代入式（5）中即可以求得每个节点位移。根据式（2）和式（3）可以分别求得每个单元的应变和应力。

2 有限元建模分析

2.1 电机轴系有限元建模

提升机电机轴系由主轴、轴承和转电机子等部分组成。由于ANSYS建模功能不方便，软件之间的联系非常重要。因此，本文采用了在SolidWorks中建模并导入到ANSYS中的方法来计算曲轴作为一个整体在转动方向上的自由振动特性。本文以某矿井7800 kW同步电机为例，根据实际尺寸在SolidWorks建立同步电机轴系模型并导入Workbench中，建模流程如图2所示。该轴系的一些参数为：材料为40Cr，密度为7800，材料的弹性模量为2.2×10 Pa，泊松比为0.3，忽略载荷对轴承的轴承刚度影响，使用单元Solid45模拟主轴。对左右两端的电机尾端的轴承支点进行固定，对左右两电机的尾端轴承面、、方向的自由度进行约束。该模型采用高精度三维20节点四面体单元（Solid95）对轴系进行自由网格划分该轴系的一些参数为：材料为40Cr，密度为7800，材料的弹性模量为2.2×10 Pa，泊松比为0.3。所建立的有限元模型如2所示。

2.2 同步电机系统轴系模型模态分析

2.2.1 有限元模态分析理论

有限元模态分析的实际上是求解在没有阻尼和外界载荷情况中多个自由度运动方程的模态矢量，通过分析可以了解某个频率范围内轴系的主要振动特性，并对种种振动源影响下的实际振动响应进行预测[16]。线弹性结构系统是轴系振动特性计算的基础，它的运动方程是一个具有有限自由度的一般线性弹性系统：

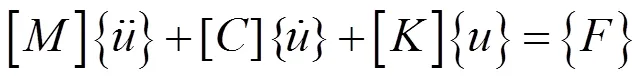
式中：[M]为系统质量矩阵，kg；[C]为系统阻尼矩阵；[K]为轴系的刚度矩阵，N/m；为轴系的节点位移，mm；为节点速度mm/s；为节点加速度，mm/s2；为外界载荷向量，N。

图2 同步电机系统轴系有限元模型

因在模态分析中，检查的是结构特定的动态属性，不依赖于外部载荷。因此，在结构的模态分析时，{}＝0。此外，由于轴系各结构的阻尼也比较小，可忽略阻尼对振动的影响。由此可得主轴的振动方程：

设式（3）的解为：

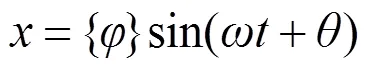
将（5）代入式（4）得：

为求得式（6）的非零解条件是其系数行列式的值为0，即：

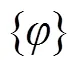
对该方程进行求解即可得出主振型{φ}（1,2,3...）。

2.2.2 同步电机轴系的模态分析

模态分析可以掌握机械轴系扭振在一定频率范围内的主要振动特性，研究双同步电机系统轴系扭振特性首先要分析其固有频率及振型。低阶固有频率比较低，低阶的模态刚度也比较低，在同样量级的激励作用下，前几阶低阶响应所占用的权值较大。所以，在对研究对象进行模态分析时，对其运动响应起主导作用的是前几阶。因此，本文对同步电机轴系进行模态分析时只提取了其前八阶的固有频率（表1）和相应的轴系振型云图（图3）。

表1 同步电机轴系固有频率

由图3给出的振型图可以看出前8阶固有频率范围分布在89～327 Hz之间，随着模态阶数的增加，模态固有频率逐渐增加，从图中可以看出弯曲振动是低阶次模态的主要振动形式，并且伴有扭转振动和轴向和轴向的伸缩振动。其中第1阶和第8阶模态振型为扭振，最大振幅分别为0.6278 mm和0.5194 mm，第2、3阶振型使电机轴系在面上进行弯曲变形，且在轴系的最后端有轻微的扭转振动现象，最大位移分别为0.87 mm和1.54 mm，第5、6阶振型使点其轴系在面上进行弯曲变形，最大位移分别为0.99 mm和1.11 mm，第4阶和第7阶是平行于面的平移振动，最大位移为0.99 mm和0.94 mm。这些扭转振动位移和弯曲位移变形将导致发生部位容易出现故障。

2.3 谐响应分析

2.3.1 谐响应分析原理

根据动力学基本方程[17]，得：

式中：()为轴系随时间变化的外界载荷函数。

因此轴系解的形式为：

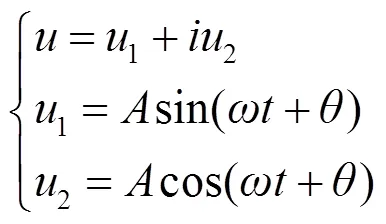
式中：为幅值，mm。

将解代入式（12），可得：

由式（14）可求解出系统谐响应的位移变化量。

2.3.2 同步电机轴系有限元分析

根据同步电机运行时的实际情况，当同步电机额定转速为750 r/min，工作状态时激励频率在50 Hz左右，在转子部位模拟加入运行时的扭矩激励，由于电机在实际运行中，轴系受振动影响最大的都是低阶频率，因此为了使响应曲线更加直观，激励频率设置为0～350 Hz，步长设置为25。同时针对精确谐波响应分析耗时大的问题，首先分析了振动频率的整个范围，通过减少子步骤和分析时间，得到了振动频率范围内主轴径向响应位移曲线如图4所示。

通过运行仿真可得轴系在工作状态下的扭振响应可以看出第一阶固有频率振型对其影响最大，即当频率为86.56 Hz时，最大振幅可达0.06 mm。随着频率的增加，每阶的固有频率对其形象会越来越小，但都会发生振动且振幅逐渐减小。因其工作频率为50 Hz，故不会发生共振危险。扭振角位移时域响应曲线及频谱曲线如图5所示。由图5可知，电机轴系的扭振角位移幅值较大的频率范围基本在50 Hz以内，且低于其1阶扭转固有频率，也说明不会发生扭转共振危险。

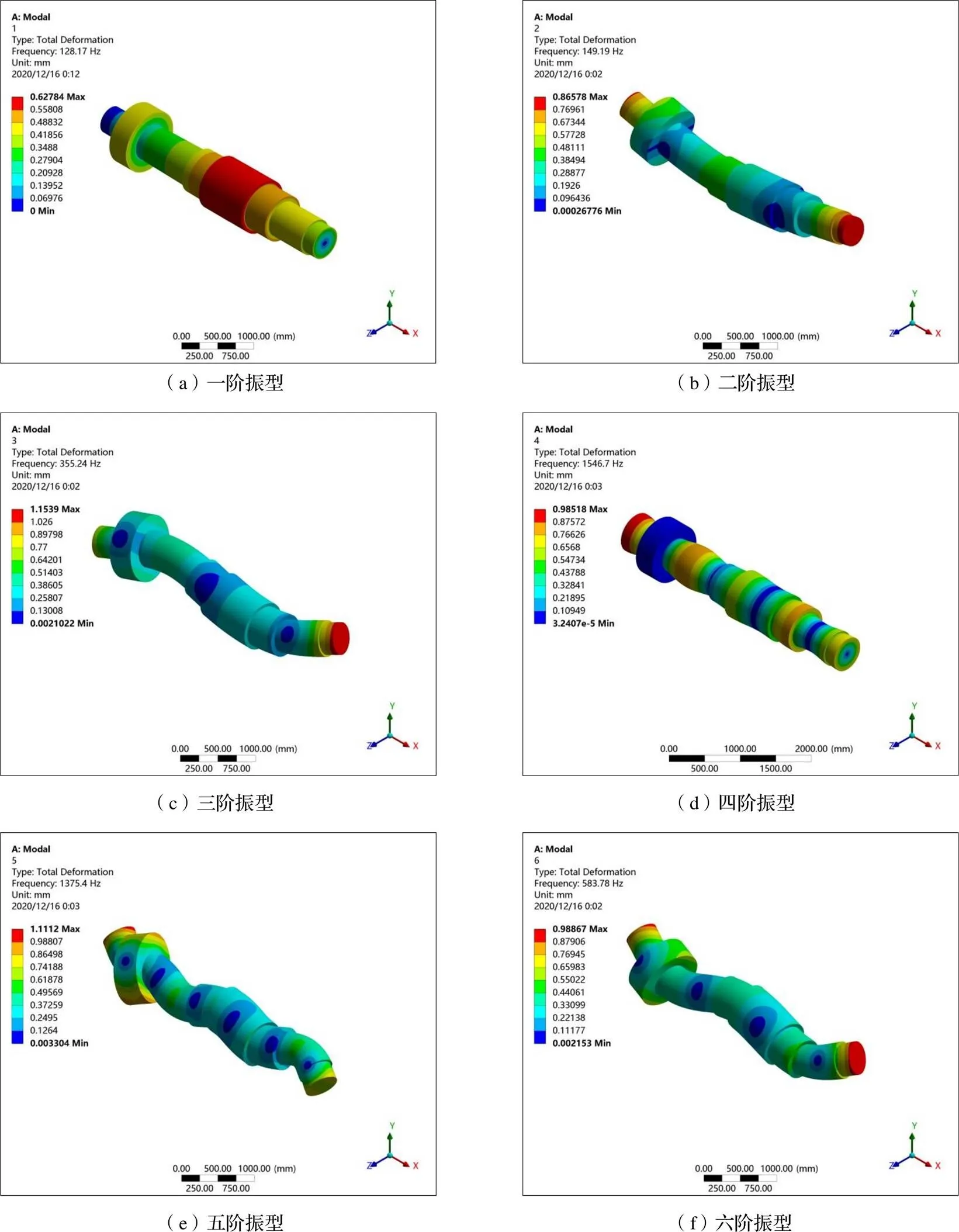
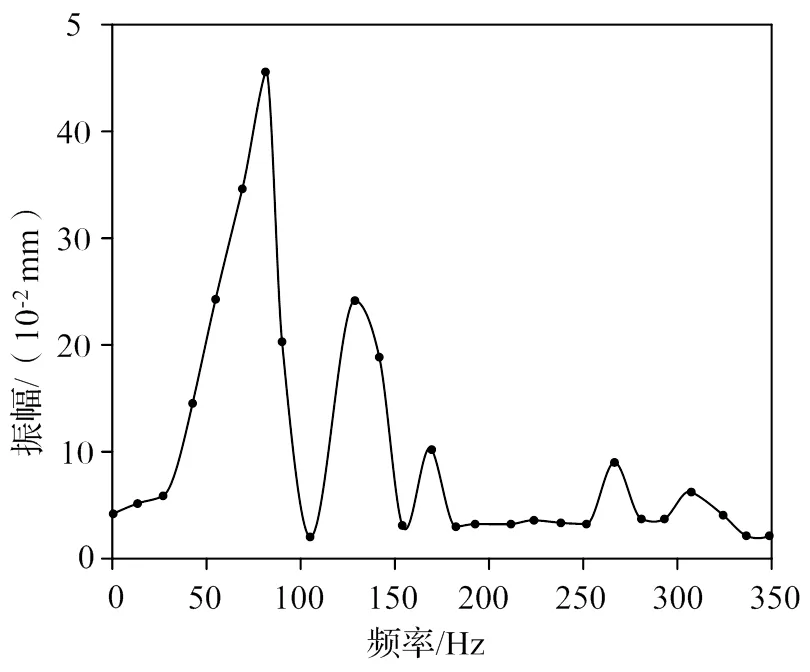
图4 谐响应分析

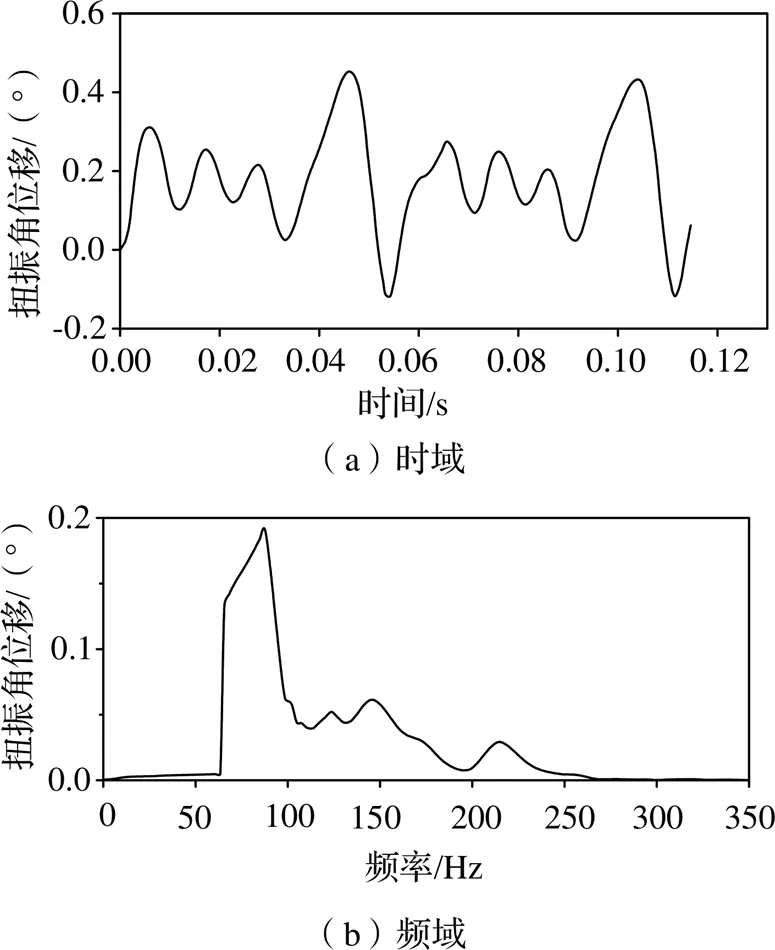
图5 扭振角位移时域响应曲线及频谱曲线

3 结论

根据对同步电机轴系进行有限元分析可得：

（1）该电机轴系前八阶固有频率均高于电机工作时50 Hz的励磁频率，因此该电机在稳定工作时轴系不会产生共振危险。

（2）通过响应分析再次验证了电机在工作时振角位移幅值较大的频率范围大于工作频率，不会发生共振现象。当频率在第一阶固有频率附近时轴系的扭转角度最大，说明发生了扭转振动现象。

（3）由模态分析的振型云图可以看出电机的振动形式以弯曲振动和扭转振动为主，最容易发成故障振动的部位是转子面附近。此外，轴的端面变形较大，容易产生较大的应力，导致电机轴系疲劳裂纹甚至断裂。因此，可考虑增加一个固定装置来限制其位移以改变结构，或通过改用刚度较大的材料来提高轴的刚度。

[1]马小亮. 利用电气阻尼抑制双环调速系统轴扭振机理[J]. 电气传动，2018，48（2）：3-13.

[2]娄东祥. 矿井提升机同步机直接转矩控制系统的研究[D]. 淮南：安徽理工大学，2008.

[3]唐艳同. 矿井提升机远程状态监测与智能故障诊断系统[D]. 太原：太原理工大学，2013.

[4]高奇峰. 矿井提升机制动系统远程监测与诊断试验研究[D]. 太原：太原理工大学，2005.

[5]Watanabe M，Iki H，Sakamoto K，et al. Analysis of Turbine Generator Shaft Torsional Vibration Caused by Self-Commutated Converters[J]. Electrical Engineering in Japan，2015，193（4）：9-17.

[6]何成兵，顾煜炯. 汽轮发电机组扭振模型和算法综述[J]. 华北电力大学学报，2003，30（2）：56-60.

[7]李晓波. 汽轮发电机组轴系建模与寿命损耗分析[D]. 北京：华北电力大学，2006.

[8]任福春，韩中合. 汽轮发电机组轴系扭振固有特性计算方法分析[J]. 电力情报，1994（3）：55-60

[9]周生通，朱经纬，周新建，等. 动车牵引驱动轴系的扭转振动特性分析[J]. 机械传动，2017，41（7）：12-17，28.

[10]陈星，苑士华，陈凯，等. 考虑电磁激励的车用永磁同步电机转子扭振特性[J]. 东北大学学报（自然科学版），2016，37（7）：1008-1012，1021.

[11]付强，袁寿其，朱荣生，等. 1000MW级核电站离心式上充泵转子轴系的扭振特性[J]. 排灌机械工程学报，2013，31（5）：394-400.

[12]Zhu Z Q，Leong J H. Analysis and Mitigation of Torsional Vibration of PM Brushless AC/DC Drives With Direct Torque Controller [J]. IEEE Transactions on Industry Applications，2012，48（4）：1296-1306.

[13]黄晓刚，蹇开林. 轧机主传动轴系扭振固有频率计算的有限元法[J]. 机械传动，2007（6）：63-66，116.

[14]任正义，周元伟，黄同，等. 电磁轴承支承下轴系转子模态及振动响应分析[J]. 机械，2018，45（9）：20-27，69.

[15]王超. 基于有限元法的某大型船用柴油发电机组轴系扭转振动分析[D]. 济南：山东大学，2018.

[16]郑传统，周杜. 基于柔性销结构的风电齿轮箱有限元仿真分析[J]. 机械，2020，47（7）：69-75.

[17]季文美，方同，陈松祺. 机械传动[M]. 北京：科学出版社，1985.

Model Analysis of Hoist Motor Shafting Based on ANSYS Workbench

GAO Feng，WANG Fuzhong，HAN Sumin

( School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China)

The main function of the hoist motor shaft is to transmit the output power of the motor to the drum through the chain drive to provide power for roller operation. It is supposed to not only meet the mechanical conditions such as strength and stiffness, but also some certain dynamic performance requirements. In this paper, the 7800 kW synchronous motor spindle is modeled by SolidWorks, and the modal analysis and the harmonic response analysis are carried out by ANSYS, and the natural frequency, mode shape and torsion angle distribution of the first eight modes of the spindle are obtained. The analysis results provide a reference for the optimal design of the motor shaft, and the resonance with excitation frequency during the operation can be avoided through reasonable optimization, which helps to improve the reliability and extend the life of the motor shaft.

motor shafting；finite element modeling；modal analysis；harmonic response analysis

TP391

A

10.3969/j.issn.1006-0316.2021.06.010

1006-0316 (2021) 06-0064-06

2020-12-17

国家重点研发计划专项（2016YFC0600906）；河南省重点研发与推广专项（科技攻关）（202102210094）

高丰（1996－），男，河北衡水人，硕士研究生，主要研究方向为双同步电机系统轴系的故障诊断，E-mail：gao15130873583@163.com。