基于BP神经网络的电场指纹点蚀信号补偿系数

吴承昊, 姚万鹏, 唐 晓, 李 焰

(中国石油大学(华东)材料科学与工程学院,山东青岛 266580)

当前石油化工领域内对腐蚀检测的需求逐渐从传统的均匀腐蚀检测转向局部腐蚀检测,其中对点蚀检测的需求尤为强烈。Jimenez等[1]认为点蚀是局部腐蚀中危害极大的情况之一,即使是不锈钢也容易产生点蚀,而普通钢材中点蚀则极为常见。点蚀的腐蚀面积很小,但其贯穿深度却很大,如果不能及时发现并准确识别其腐蚀深度,将会给在役的压力容器和管道造成很大的安全隐患。电场指纹技术(field signature method,以下简称FSM)是20世纪末发明并推出应用的一种腐蚀检测技术[2],主要根据被检测结构表面因腐蚀而造成的电压变化,对被测结构的腐蚀情况进行判定,对多种腐蚀类型都有着极高的灵敏度。20多年来,随着FSM不断在国内外获得应用及推广[3-6],对其认识也不断深化,但是该方法对点蚀信号的识别及高精度检测一直是一个难题。国外现有型号设备的精确度也只能达到±10%WT(WT为管道壁厚)[7-8],文献中相关报道只是通过对电场指纹系数(fingerprint coefficient,简称FC)的计算后乘以取值为3～5的经验系数,对点蚀坑的腐蚀深度进行计算、补偿[5],但是并未说明其技术细节。点蚀信号的参数辨识需要将相关检测数据发回生产厂商进行具体分析和计算后再告知用户结果,对腐蚀检测结果的时效性产生很大的消极影响,补偿方法的普适性较差。笔者通过对点蚀的FSM信号进行数值模拟和仿真,根据点蚀信号的分布特征提出一种基于BP神经网络的点蚀补偿系数计算方法,并利用神经元网络的非线性映射能力,建立不同腐蚀形貌的补偿系数模型,能有效逼近当前腐蚀位置的修正系数,进而准确辨识腐蚀深度。

1 FSM原理及点蚀误差分析

1.1 FSM原理

电场指纹技术原理是在被测对象的两端设置电极并通以直流电,在被测对象上布置采集电极,通过采集到的电压变化来判断是否发生腐蚀。当腐蚀发生时电场线随之发生变化,因此将采集电极中采集到的电压与最初没有发生腐蚀时的电压相比较,可以获得每个检测网格内的电压变化,这种电压变化称为电极对的电场指纹系数。电场指纹系数用以判断腐蚀速度和腐蚀积累。每一个电极对电场指纹系数的计算表达式[2]为

FCAi=1 000(UBUAi/(UAUBi)-1).

(1)

式中，FCAi为i时刻电极对A的指纹指数；UA为启动时电极对A的电压,V；UB为启动时参考电极对B的电压,V；UAi为i时刻电极对A的电压,V；UBi为i时刻电极对B的电压,V。

(2)

式中,I为恒定直流电,A；ρ为电阻率,Ω·m;W、L和T分别为宽度、长度和厚度，mm。

长度L、宽度W是根据采集电极布置时检测网格大小所确定的每个检测网格的固定值，在温度不发生改变情况下电阻率ρ为常数，则采集电压仅与被测对象的壁厚T成反比。这说明当被测对象发生腐蚀时，即被测对象厚度变化，可以测量相对应的电压变化，然后将其与被测对象最初的采集电压进行比较，可以推导出电压变化与被测对象壁厚变化之间的关系。

常见的点蚀一般为圆柱形或圆锥形，其腐蚀形貌对计算的影响包括深度和半径两部分，从式(2)中可以看出电场指纹系数只对应深度一个变化量，电场指纹系数反映的是整个检测网络内的平均腐蚀厚度；而点腐蚀的半径一般很小，所以现有报道中表示需要乘以经验系数做补偿。

1.2 点蚀误差分析

在点蚀测定和计算方面传统的计算方法中未考虑腐蚀面积和腐蚀位置的影响，而是先根据式(1)和(2)计算一个腐蚀深度，然后再乘以经验系数(取值为3～5)进行补偿[3],表示为

(3)

式中，Ht为t时刻的实际腐蚀深度,mm；H0为初始壁厚,mm；Hc为根据电场指纹系数计算得到的腐蚀损失,mm;FC为电场指纹系数。

即使是相同形态和尺寸的点蚀，因其萌生的位置与检测网络中布设采集电极的相对位置不同，得到的电场指纹系数也有很大出入，所以点蚀计算中还有相对位置这一变量，即

FC=f(S,D,P).

(4)

式中，S为腐蚀面积；D为腐蚀深度；P为腐蚀位置。

显然传统的计算方法中,通过乘以经验系数的计算方法很可能会引入较大的系统误差,本文中将通过数值仿真方法定量分析经验公式的误差问题。

采用COMSOL Multiphysics软件对Q235钢进行仿真模拟,电场的初始条件和边界条件为

J=σE+Je,

(5)

E=-U,

(6)

(7)

n·J=0,

(8)

U=0.

(9)

式中,E为电场强度,V/m;U为电压,V;J为电流密度,A/m2;Je为外加电流密度,A/m2;σ为电导率,S/m;QJ,V为电流源,A/m3。

式(5)～(7)是麦克斯韦方程在低频时的表现形式,式(8)是模型中表面的边界条件,式(9)为电流电极中接地端的边界条件。

根据点蚀在检测网络中与检测区内采集电极对的相对位置不同,建立不同的有限元模型。如图1所示,每一个由点划线确立的大正方形网格为一个电极对的有效检测区域(即一个单独的测量区域),电极间距为20 mm,而每个红点代表一个采集电极。实线确立的小正方形则是某个点蚀萌芽和成长的区域。

图1 腐蚀位置示意图

根据图1中每个不同的腐蚀萌生位置进行建模,数据样本号是根据腐蚀萌生位置的不同从第一行开始从左至右、从上至下分别为1#～9#。图2为模拟建模示意图,图中红点代表采集电极,试板(600 mm×200 mm×10 mm)中腐蚀位置处于检测网格中心位置(样本5#),模拟的腐蚀为圆柱形腐蚀小孔,半径为5.00 mm,深度为2～4 mm,其中两侧圆柱为电源馈入馈出电极。数据处理后,得到的点蚀坑所在检测网格的电场指纹系数如表1所示。当点蚀坑深度为2、3和4 mm时,电场指纹系数分别在32.1～104.8、52.3～137.8和75.31～174.9变化。

图2 模拟建模示意图

表1 点蚀坑与采集电极网络相对位置不同时的电场指纹系数

由表2可以看出,当点蚀坑处于检测网格的不同位置时,同一个采集电极区域会有不同的电场指纹系数;如果在对腐蚀检测信号进行参数辨识时不考虑点蚀坑与采集电极网络的相对位置因素,将会造成极大的误差,而这种误差会随着腐蚀深度的变大而变大。表1中最小的电场指纹系数出现在样本4#(6#)而最大的电场指纹系数为样本2#(8#)。以这两个腐蚀位置为例,按照传统的电场指纹计算公式(1)计算出电场指纹系数后,再乘以经验系数计算腐蚀深度,如表2所示。

表2 不同位置下相同腐蚀的腐蚀深度计算

由表2可以看出,相同尺寸的腐蚀,因为所在位置不同计算所得到的电场指纹系数也不同,进而计算出的腐蚀深度是不同的;相同尺寸的腐蚀因为位置不同所需要的经验系数也是不同的,如果没有选择准确、可靠的经验系数,将会产生很大的系统误差;而相同位置的腐蚀因为其尺寸不同所需要的经验系数也有所区别,如果不能可靠地确定系数,也将产生较大的系统误差。

式(4)中影响电场指纹系数的还有腐蚀面积的因素,而腐蚀面积主要受点蚀坑半径的变化影响,通过数值模拟和仿真得到的数据,绘制了电场指纹系数与点蚀深度h之间的关系,如图3所示。由图3可以看出,当点蚀深度h一定时,通过函数分析得到,电场指纹系数与点蚀半径r呈现一种幂函的关系,不同深度下的曲线其底和指数不同。可见这种非线性关系,只是简单的用经验系数对点腐蚀情况进行分析依然存在较大系统误差。

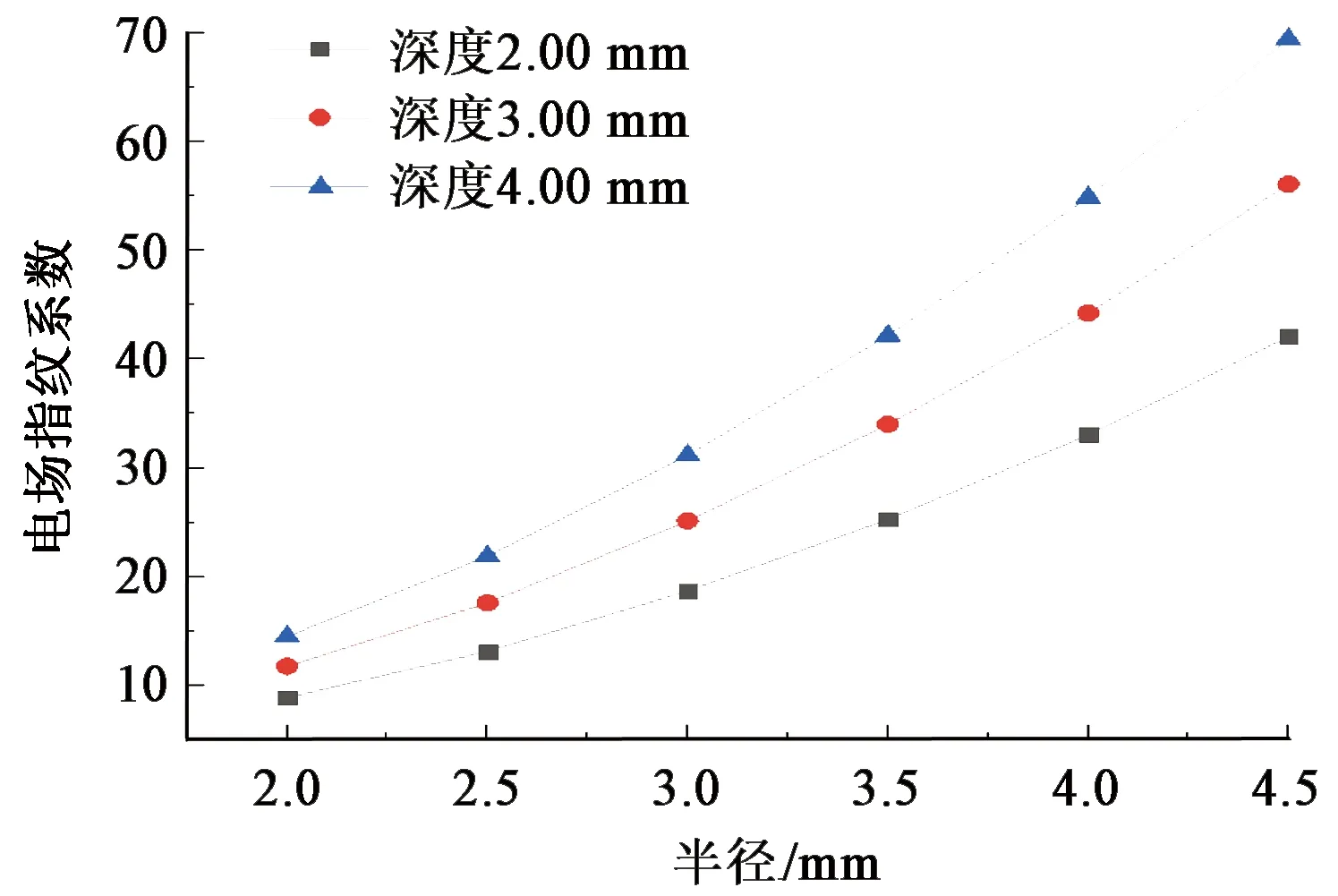
图3 FC值与腐蚀半径关系

综上所述,现有报道中采用经验系数来修正是不能准确地修正因为腐蚀尺寸和腐蚀位置造成的电场指纹系数变化,从而无法逼近实际腐蚀情况,造成较大的系统误差。

2 点蚀深度求解

如表1、2所示,较为笼统地使用经验系数取值为3～5的方法计算点蚀深度,除算法原理不明外,计算结果误差较大。因此建立了补偿系数计算方法替代经验系数方法。本文中所定义的补偿系数就是实际腐蚀深度所对应的电场指纹系数与采集数据计算出的电场指纹系数的比值。将实际腐蚀测量得到的电场指纹系数乘以补偿系数,即可求得较为准确的腐蚀深度。通过数值仿真计算得到不同腐蚀情况下的电场指纹系数,并采用BP神经网络的方法建立数学模型,基于BP神经网络强大的非线性映射来计算不同点蚀位置及形貌参数相对应的补偿系数[9]。

2.1 样本空间建立

图4为对数值仿真模型进行数据提取和分析的局部检测网格示意图。通过数值仿真发现,局部腐蚀位置或深度变化对腐蚀发生区域及其上下左右4个检测网格的电场指纹系数影响最大,因此将发生腐蚀区域的电场指纹系数定义为FCC,腐蚀区域上下左右4个检测网格的电场指纹系数定义为FCU、FCD、FCL、FCR。通过模拟不同位置、直径、深度的点蚀缺陷,将提取并计算获得的5个电场指纹系数作为输入参量,将与真实腐蚀深度对应的补偿系数作为输出参量,建立样本空间。其中点蚀位置为图1所示的9种情况,点蚀直径分别为2、3和4 mm三种情况,点蚀深度为3、4和5 mm三种情况,共81组数据为训练样本,样本号为1#～81#,如表3所示。再随机选取不同腐蚀位置为例做检测样本,点蚀深度分别为2、3、4和5 mm,共4组数据检测样本,样本号为82#～85#。在进行算法分析时,对样本数据进行随机化处理,确保算法分析结果的独立性。

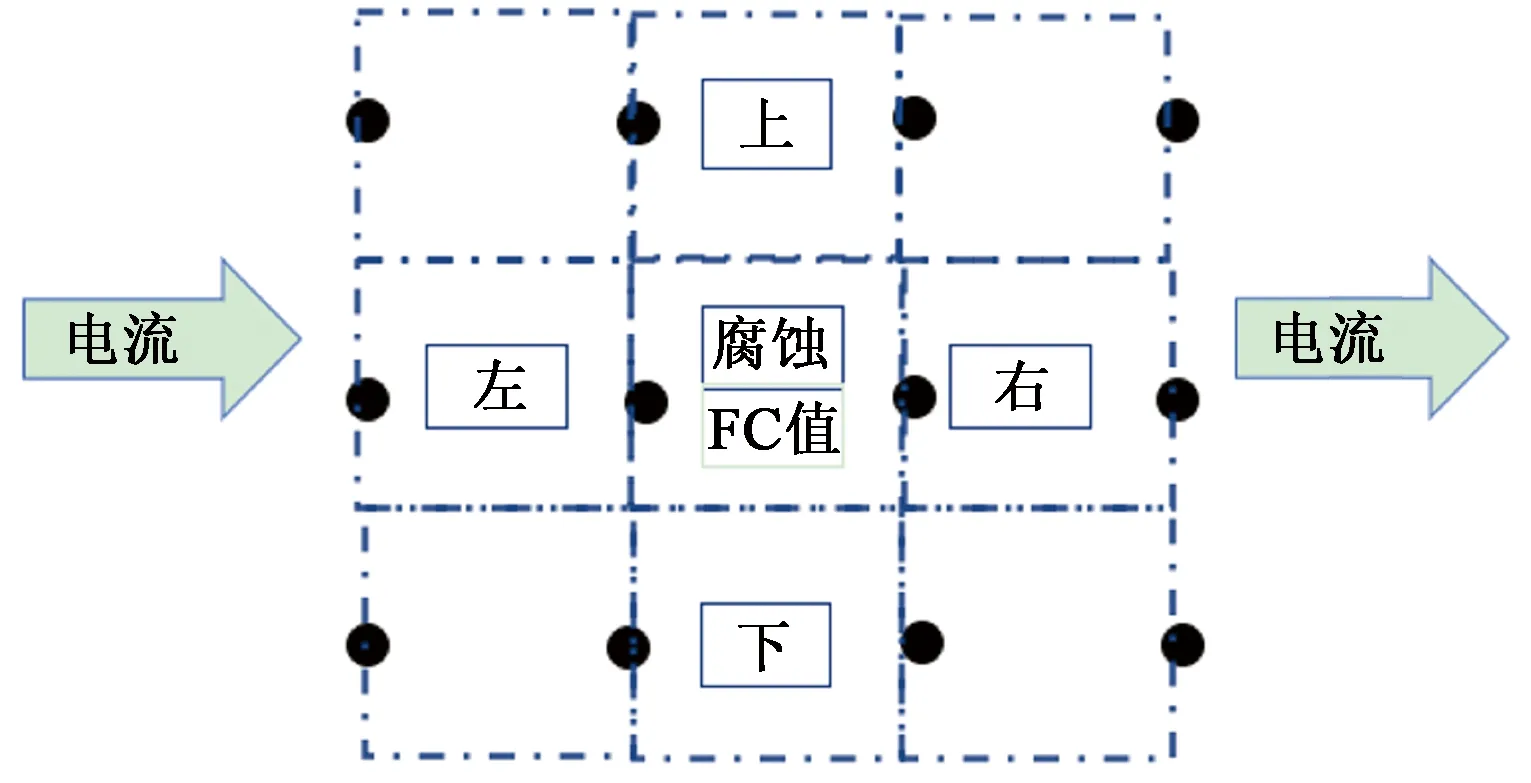
图4 腐蚀检测网格示意图

表3 不同尺寸腐蚀的特征信号FC及补偿系数

2.2 BP神经网络结构设计

网络隐含层的神经元传递函数采用S型对数函数logsig,输出层的神经元传递函数采用线性函数purelin。采用Trainlm函数对网络进行训练,并确定学习速率为0.05,目标误差为1×10-10,最大训练次数为1 000。动量系数取0.9,可避免算法陷入局部极小,加快学习速度[12-13]。

2.3 神经网络计算结果

根据样本数据进行了BP神经网络训练,网络训练第6次可达到目标误差。根据样本数据进行BP神经网络训练后,检测结果如表4所示。可以看出,训练后得到的测试结果与通过仿真数据计算所得到的真实值接近,相对误差小于±5%,得到较好的训练结果。利用预测所得补偿系数计算点蚀的腐蚀深度,并与经验系数的计算方法(图中是经验系数为5的计算结果)及真实腐蚀深度进行比较,结果如图5所示。由图5可以看出,采用神经网络模型计算出的补偿系数的方法优于传统补偿系数的方法,误差小,能够较准确地反映实际腐蚀情况。这表明基于BP神经网络的补偿系数模型有较高的预测精度,可以用于计算实际FSM腐蚀检测时点蚀坑的深度。

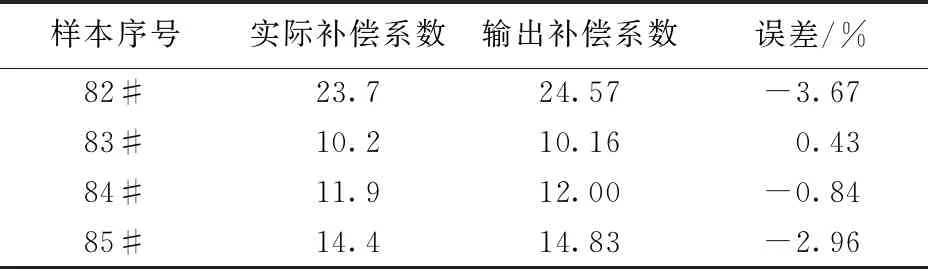
表4 BP神经网络测试的输出结果

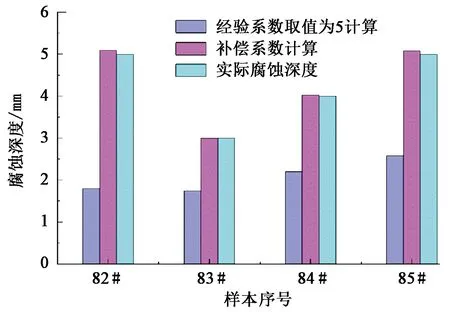
图5 计算腐蚀深度对比

3 试验验证

为了验证基于BP神经网络计算补偿系数方法的准确性,制作不同位置、不同尺寸的腐蚀试样,如图6所示。图6(a)中点蚀坑半径为2.70 mm、深度为2.30 mm,图6(b)中点蚀坑半径为3.20 mm、深度为2.70 mm。焊接螺柱是电压采集点,每个采集点之间间隔为20 mm。

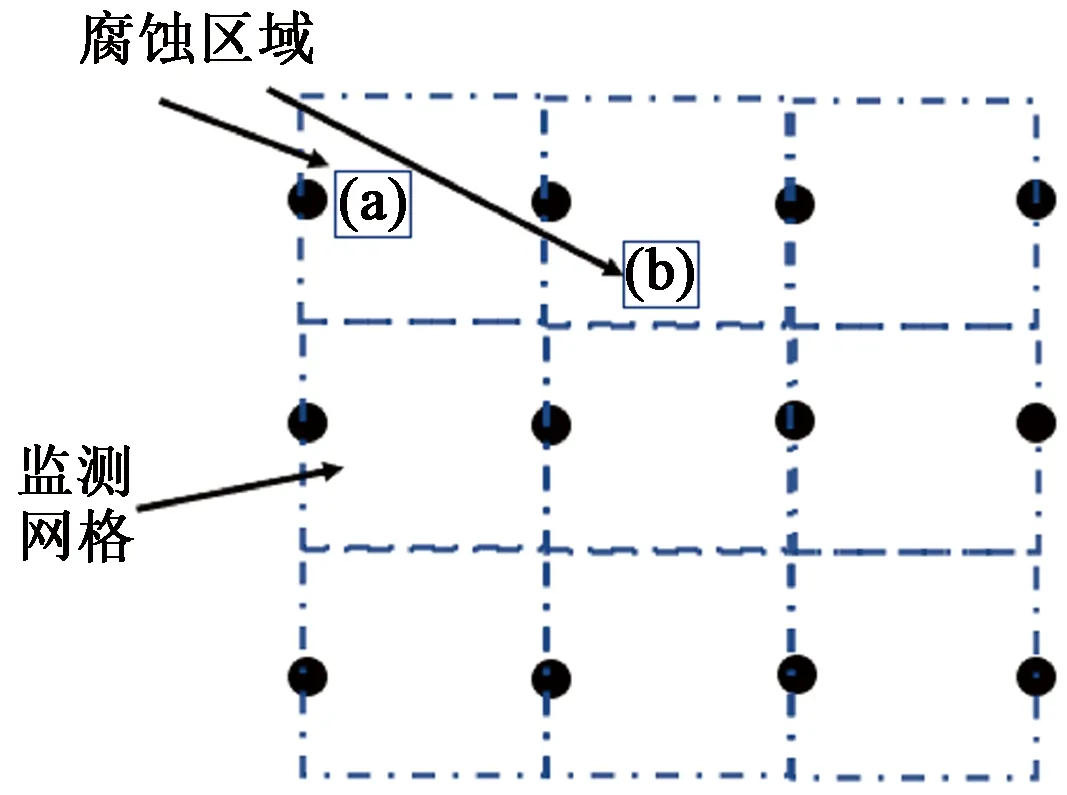
图6 腐蚀试样示意图

试验设备是本试验室自主研发的电场指纹系统[14-15],由PXIe的硬件平台和LabVIEW软件平台组成。利用LabVIEW中可调用并可编写MATLAB脚本的功能,将脚本直接写入LabVIEW程序中。

首先根据采集电压信号计算腐蚀信号的特征值,然后基于模拟建立的BP神经网络模型进行补偿系数计算,最后根据得到的补偿系数计算腐蚀深度。试验结果如表5所示。

表5 试验验证结果

从表5中可以看出,应用神经网络模型计算出的补偿系数计算得到的腐蚀深度与真实值极为接近,不会因位置和腐蚀尺寸的不同而影响检测精度,误差满足检测精度要求,能够为局部腐蚀检测提供准确信息。

4 结束语

通过对点蚀的FSM信号进行数值模拟和仿真,分析了点蚀信号分析计算中误差存在的主要原因,根据点蚀信号的分布特征提出一种基于BP神经网络的点蚀补偿系数计算方法,并利用神经元网络的非线性映射能力,构建的3层BP神经网络对不同位置和尺寸的点蚀数据样本进行建模、训练和测试,能有效逼近当前腐蚀位置的修正系数,进而准确辨识腐蚀深度。与传统点蚀深度计算方法中只是简单的使用经验系数取值为3～5的方法,本方法得到的结果检测精度高,解决了经验系数补偿方法中普适性差、精准度不高的问题。