斜井各向异性地层阵列侧向测井资料快速分级反演方法

范宜仁, 吴易智, 李潮流, 巫振观, 袁 超, 邢 涛

(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580; 2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071；3.中国石油勘探开发研究院,北京 100083)

随着油气勘探的日益深入,为克服复杂多变的井周环境,具有优良聚焦能力的阵列侧向测井技术被广泛使用。其中斯伦贝谢公司、阿特拉斯公司以及中油测井公司相继研发的高分辨率阵列侧向测井仪器HRLA、HDLL和HAL均取得商业化应用。该类仪器具有较高的纵向分辨率,能够提供5～6条不同探测深度的测井曲线,极大丰富了井下地层信息,为油气层的识别提供了更可靠的资料[1-6]。虽然阵列侧向仪器纵向分辨率高,但其受围岩、侵入和各向异性等因素影响严重,测量得到的原始视电阻率曲线难以反映地层真实电阻率,采用反演手段则可以充分考虑各种因素影响,从而有效提取地层真实电阻率[7]。目前,阵列侧向测井资料1D和2D反演技术已经趋于成熟[8-11]; 3D反演的问题主要在于三维正演难度大,反演速度较慢[12-16]。目前来看,当前反演技术主要存在以下几个问题:①阵列侧向响应复杂,主控因素难以界定;②反演参数众多,初值选取困难;③各向异性导致代价函数收敛速度慢,反演耗时长。笔者从曲线分离特性出发,首先基于3D有限元算法确定曲线分离因子对不同地层参数的敏感性强弱;然后,采用初值分级选取策略并结合Levenberg-Marquradt算法,实现倾斜各向异性地层的快速反演;进一步利用数值模拟验证反演算法的稳定性和准确性,并将研究结果用于实际井资料分析。

1 各向异性地层阵列侧向测井响应特征

1.1 阵列侧向测井原理

以斯伦贝谢公司的HRLA为例,其电极系结构如图1所示。该仪器由主电极A0、6对屏蔽电极A1～A6(A1′～A6′)以及两对监督电极M1、M2(M1′和M2′)组成,通过改变不同电极间的收发组合方式,可以形成6种具有不同探测深度的电阻率曲线,依据探测深度由浅及深原则,电阻率曲线分别命名为RLA0、RLA1、RLA2、RLA3、RLA4、RLA5,其视电阻率计算公式为

图1 HRLA电极系结构示意图

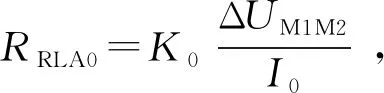
(1)

(2)

式中,UM1M2和K0分别为第一种探测模式下监督电极M1和M2之间的电势差以及电极系数;i=1,…,5代表上述5种探测模式;Ki为第i种探测模式的电极系数;RRLAi为第i种探测模式的视电阻率;UM1为监督电极M1处电位;I0为主电极电流。

另外,为研究地层参数对阵列探测曲线分离程度的影响,定义分离因子F如下:

(3)

式中,i=2,…,5代表阵列侧向第2～5种探测模式。

1.2 层厚和围岩的影响

建立含井眼三层地层模型:井眼直径为0.203 2 m,钻井液电阻率为0.05 Ω·m,目的层电阻率为20 Ω·m,围岩电阻率为2 Ω·m。图2为仪器位于目的层中点时阵列侧向测井视电阻率随目的层层厚变化。从图2中可以看出，随着目的层层厚的增大,阵列侧向5种探测模式测量值逐渐增大,并逐渐分离。当层厚在0.6～1.0 m时,由于在仪器分辨率范围内,浅探测模式的电流受围岩分流影响,而深探测模式聚焦能力较强,导致曲线呈正差异,此时5条曲线分离因子接近1.12;当层厚大于1.0 m时,围岩对深探测模式的影响变大,曲线出现翻转,呈负差异现象,当层厚大于40 m时,阵列侧向5种探测模式均反映目的层电阻率,5条曲线重合,此时阵列侧向响应不受围岩影响。

图2 视电阻率随层厚变化曲线

1.3 各向异性和地层倾角的影响

为分析各向异性和倾角对曲线分离程度的影响,建立无侵入地层模型:钻井液电阻率为0.05 Ω·m,井眼直径为0.203 2 m,各向异性系数λ变化范围为1.0～3.0,地层倾角θ(井眼与地层界面法线方向夹角)变化范围为0°～90°,地层水平电阻率Rth为30 Ω·m。结果如图3所示,其中图3(a)为λ和θ对浅探测模式分离度的影响,即F2;图3(b)为λ和θ对深探测模式分离度的影响,即F5。

图3 低侵条件下各向异性系数对曲线分离度的影响

可以看出,在λ和θ的联合作用下,阵列侧向探测曲线的分离因子最大接近1.2;低角度条件下,曲线呈负差异,角度越低,分离越大;高角度条件下,曲线呈正差异,且角度越高,分离越大。

图4为θ为0°条件下各向异性系数对阵列侧向曲线的影响。可以看出,各向异性系数导致5种探测模式测量值抬升,各向异性系数越大,抬升幅度越大。当各向异性系数为3时,抬升幅度最大约50%。通过分析不同地层条件下的响应规律,明确了各向异性和地层倾角对阵列侧向测井5种探测模式分离度的影响,为阵列侧向反演方法的研究提供了理论基础。

图4 视电阻率随各向异性变化

1.4 钻井液侵入的影响

考虑直井有侵各向同性地层,研究钻井液低侵对阵列侧向曲线分离程度的影响。建立钻井液侵入地层模型一:钻井液电阻率为0.05 Ω·m,井眼直径为0.203 2 m,地层倾角为0°,侵入带电阻率Rxo为5 Ω·m,图5为钻井液侵入对曲线的影响,可以看出,钻井液侵入导致5种探测模式测量值下降,侵入深度越大,下降幅度越大,当侵入深度为1.5 m时,下降幅度最大约90%。

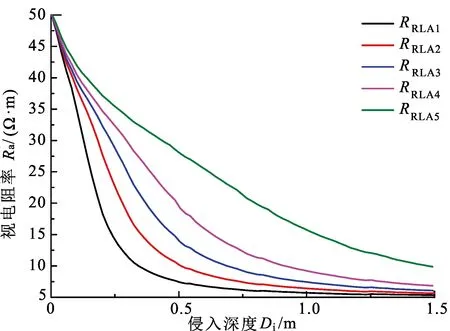
图5 视电阻率随侵入深度变化

建立侵入地层模型二:钻井液电阻率为0.05 Ω·m,井眼直径为0.203 2 m,地层倾角为0°,Rxo为0.5 Ω·m,原状地层与侵入带电阻率比值Rt/Rxo变化范围为1～20,侵入深度Di变化范围为0～2 m。结果如图6所示,其中图6(a)为Di对浅探测模式分离度的影响,即F2;图6(b)为Di对深探测模式分离度的影响,即F5。可以看出,Di使得阵列侧向探测曲线的分离因子最大接近于10,且Di在0.4～0.6 m之间最大。

图6 低侵条件下侵入深度对曲线分离度的影响

由上述分析可知,较之各向异性和地层倾角,钻井液侵入对地层的阵列侧向曲线的影响最大,即在有侵各向异性倾斜地层中,阵列侧向响应对侵入较为敏感,各向异性和地层倾角次之。该结论为阵列侧向分级快速反演方法的建立奠定了理论基础。

2 阵列侧向测井分级快速反演

2.1 反演流程

由于阵列侧向测井响应影响因素复杂多样,其视电阻率曲线较难反映地层真实电阻率,所以对其进行反演处理是获取地层真实电阻率的有效途径。为此,首先明确了阵列侧向测井响应中包含的地层参数信息,依据分离因子对其敏感性进行分级;构建阵列侧向响应数据库,将数据库可视化,即建立初值选取图版;然后采用初值分级选取策略实现阵列侧向反演的初值优化选取,从而减少反演迭代次数,为反演速度的提升提供了保障;最后,为解决一般梯度类反演算法全局寻优能力弱(梯度下降法)、收敛速度慢(高斯-牛顿法)的难题,采用Levenberg-Marquardt算法,进而提升了反演精度。图7为反演流程。

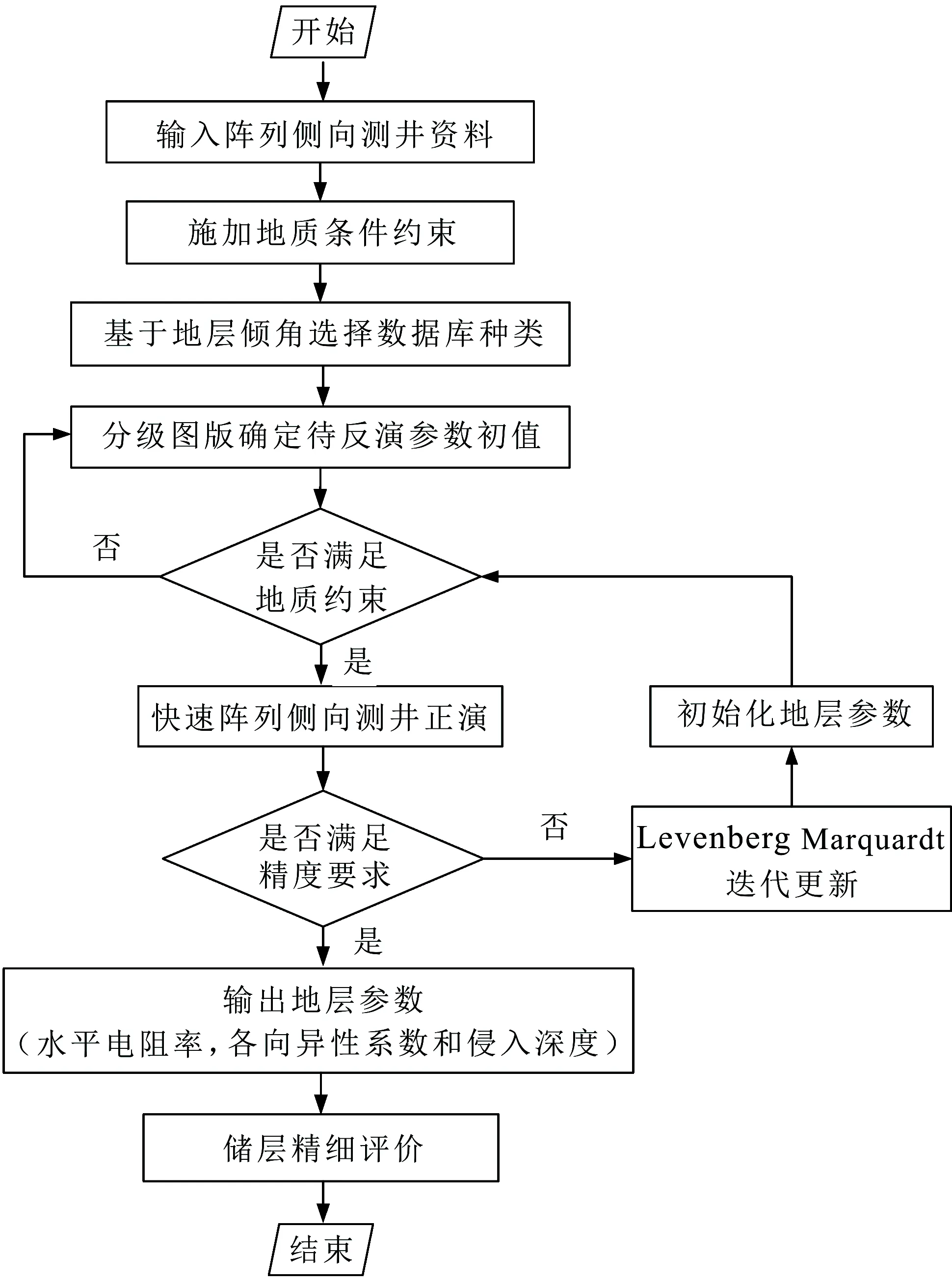
图7 分级反演流程

2.2 Levenberg-Marquardt反演算法

阵列侧向测井的反演是典型的非线性反演问题,其代价函数变化剧烈且存在多个局部极小值,为了提升反演精度以及实现阵列侧向测井电阻率剖面的快速精准重构,采用Levenberg-Marquardt(L-M)反演。L-M算法结合了梯度下降法与高斯-牛顿法的优点,在保证最优搜索方向的同时提升算法的收敛速度。其基本的思想是通过有效迭代寻出非线性最小二乘函数的最小值:

(4)

其中

x=(Di1,Rxoh1,Rth1,λ1,…,Din,Rxohn,Rthn,λn)T.

采用L-M算法和信頼域方法[17-18],反演过程中的第k+1步更新迭代为

(5)

式中,I为单位矩阵;α为Levenberg-Marquardt正则化参数;J为雅克比矩阵;D为缩放矩阵;h为信赖域半径。

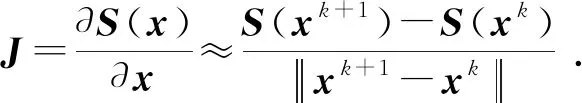
(6)

通常情况下,雅克比矩阵是根据有限差分法进行求解,如式(6)。但此处反演参数众多,雅克比矩阵的求取耗时较长,所以为提高雅克比矩阵的计算速度,本文中采用Broyden近似方法进行J的迭代更新[19]:

(sk)T.

(7)

式中,sk为第k步迭代过程,sk=xk+1-xk。

由于二维反演受到地层垂向和径向上多种参数的影响,即使基于一阶Broyden等效近似方法仍无法解决初步迭代阶段雅克比矩阵计算困难的问题。为此,采用Yin等[20]提出的开窗技术以及参数分离反演方案来提升反演速度。

式(7)中e(x)可以表示为

(8)

而阵列侧向仪器HRLA的响应函数S(x)可以用映射运算符G和地层参数矢量x表示:

(9)

其中

x=(x1,x2,…,xN)T.

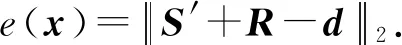
(10)

式(10)只在初步迭代过程中被用来计算雅克比矩阵,而其余雅克比矩阵的更新迭代则采用一阶Broyden等效近似方法。本文中通过结合两种计算方法,极大地提高了阵列侧向反演的速度和精度。

除此之外,每次迭代中还需对正则化参数ω进行更新,这里采用[21]所述的方法进行更新:

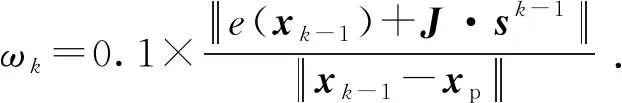
(11)

2.3 初值分级选取策略

对确定性反演算法而言,反演结果很大程度上依赖于初始模型参数的选取,且对于各向异性地层来说,反演参数包括侵入深度Di、侵入带水平电阻率Rxoh、原状地层水平电阻率Rth和各向异性系数λ。可以看出,反演参数复杂多样,从而导致迭代次数较多、耗时较长,难以达到阵列侧向测井反演的速度要求。为了提升反演的收敛速度,必须合理选取反演初值。为此,建立不同地层倾角下的数据库,根据不同参数对阵列侧向测井响应的敏感性,采用分级选取策略,实现4个反演参数初值的快速最优选取。具体步骤如下:

(1) 构建阵列侧向响应数据库,参数范围为θ=0°～90°,Di=0.1～1.5 m,Rxoh=0.3～30 Ω·m,Rth/Rxoh=1～20,λ=1～2.5,基于3D有限元技术,根据地层倾角对数据库进行分组构建,其中地层倾角为数据库首选参数。

(2) 基于阵列侧向测井5种探测模式曲线分离程度的不同,建立λ-Rxoh型交会图,如图8(a),利用插值计算方法确定侵入深度Di0。

(3) 在侵入深度Di0的基础上,建立一系列λ-Di0型交会图,如图8(b),根据插值计算,确定侵入带水平电阻率、原状地层水平电阻率,最后根据选取电阻率初值时对应的图版类型,确定各向异性系数。为验证初值选取策略的稳定性和准确性,以0°倾角数据库为例,选取不同地层条件下的模拟点进行验证。首先验证λ-Rxoh型交会图选取结果的准确性,验证结果见表1。

表1 λ-Rxoh型交会图验证结果

图8 初值选取图版

可以看出,根据λ-Rxoh型交会图能够很好地确定出Di,相对误差小于5%,且Di的确定基本不受侵入带电阻率变化的影响,但对原状地层电阻率影响较大,说明侵入深度对阵列侧向响应的影响较大,这一结论与上节得出的结论一致,即侵入深度是阵列侧向测井响应的主控因素。

在此基础上采用λ-Di型交会图确定地层侵入带水平电阻率以及原状地层水平电阻率值,验证结果见表2。

由表2知,根据已判定的侵入深度匹配相应的λ-Di型交会图,利用插值计算方法可以确定出地层侵入带与原状地层水平电阻率(Rxoh和Rth)以及各向异性系数λ,可以看出,交会图对水平电阻率的识别误差约为10%,效果好于各向异性系数(20%),其结果满足初值选取需要。

由此发现,通过初值分级选取策略可以有效地为Levenberg-Marquardt算法提供较为准确的反演初值,从而在反演过程中减少了迭代次数,使得反演速度得到有效提升,每个测量点反演耗时1.5 s,比传统3D反演提高近7倍。同时该策略摆脱了局部极小值的困扰,保证了反演结果的精度。

3 算法验证与实际资料处理

3.1 反演算法验证

为验证反演算法的准确性和稳定性,建立井径为0.203 2 m,钻井液电阻率为0.1 Ω·m的井眼环境,并采用24层的有侵入各向异性俄克拉荷马模型。如图9所示,该模型的层厚H变化范围为0.9～6.0 m;Di范围为0.0～1.2 m;Rxoh范围为0.2～50.0 Ω·m;原状地层水平电阻率Rth范围为0.7～150.0 Ω·m;各向异性系数λ变化范围为1.0～2.5。

由图9(c)中可以看出,无侵入、各向异性和地层倾角影响时阵列侧向能够识别地层真实电阻率,如模型第1层;当地层只存在各向异性和倾角影响时,如图9(d)中模型第14层,该层无侵入,地层倾角为60°,各向异性系数为1.2,此时可以看出,HRLA曲线分离程度(F5)范围为1.19～1.41;当地层只有侵入影响时,如图9(c)中模型第23层,侵入深度为0.5 m,地层倾角为0°,各向异性系数为1,此时曲线分离程度F5范围为5.19～10.21。可以看出,侵入对阵列侧向响应影响较为显著,从而验证了1.3与1.4节分析结果的正确性。

图9 模型参数分布及HRLA响应

通过对该模型进行反演处理,可以得到侵入深度、地层水平电阻率、各向异性系数以及反演参数总的相对误差曲线,如图10所示。可以看出,地层倾角为0°时,反演后的侵入深度以及地层水平电阻率与原始模型一致性较高,反演误差小于5%,且地层侵入剖面与电阻率剖面能够得到精确划分;对于各向异性系数,虽然在λ较大地层反演结果在地层界面处出现分散,但对于绝大部分地层,地层界面仍能够得到很好地划分;对于地层倾角为60°的地层,由于倾角的影响,反演结果的总相对误差增大,但侵入深度和水平电阻率曲线仍能够准确提取。

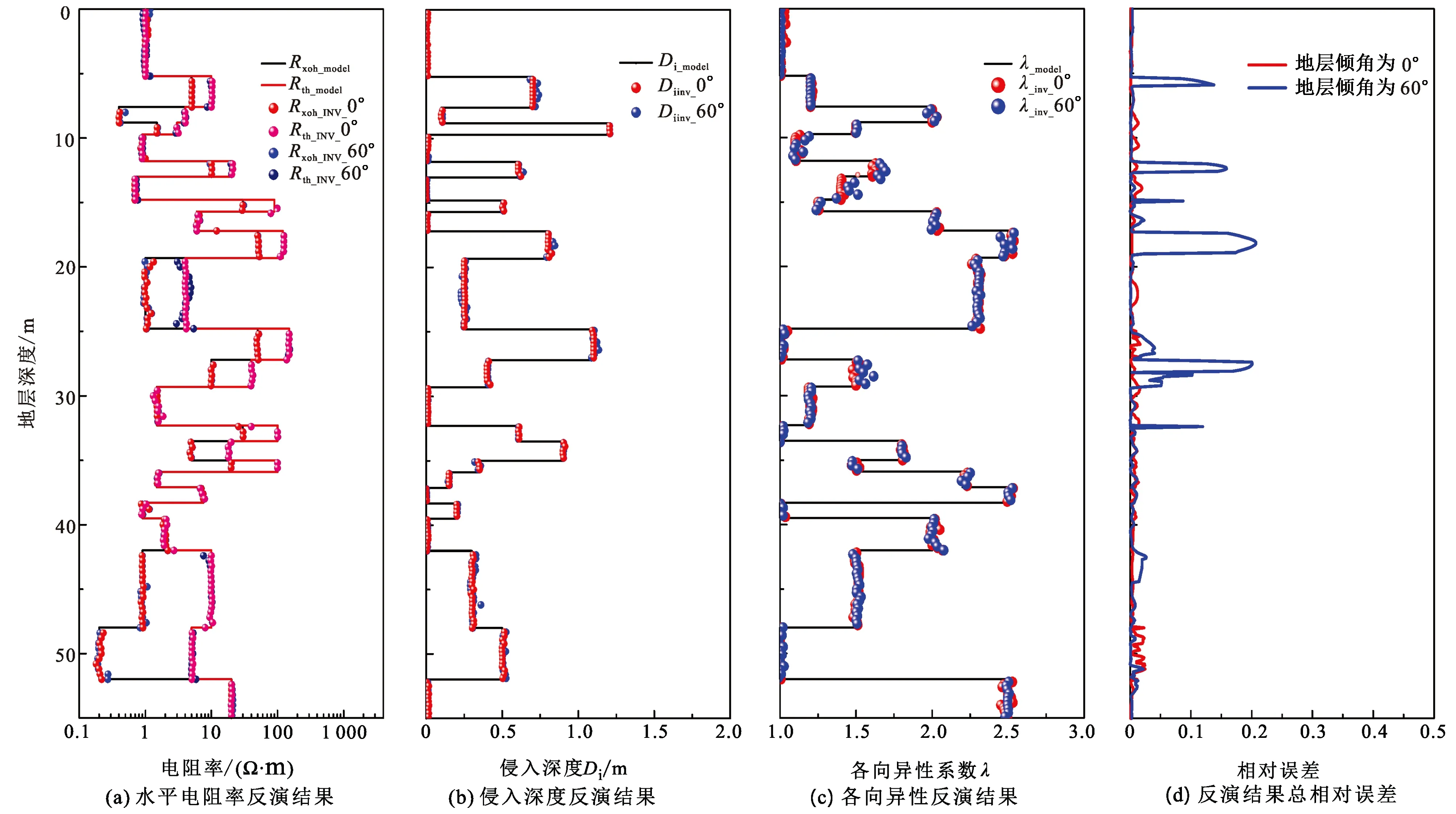
图10 模型反演结果

对于有侵入倾斜地层的阵列侧向测井资料,通过将初值选取策略与Levenberg-Marquardt优化算法相结合的方法,实现了侵入深度与地层水平电阻率的精确提取,对井下复杂地层环境下的电阻率剖面与侵入剖面的精确划分提供了有力支持,为油气藏的识别、储层精细评价以及产能精准预测奠定了坚实的基础。

3.2 实际资料处理

将上述反演算法应用到青海英西油田X井的阵列侧向测井资料,其解释结果如图11所示。该井段为砂泥岩剖面,井眼钻井液电阻率为0.1 Ω·m,深度范围为4 160.67～4 180.00 m;第三道为实测阵列侧向测井曲线;第四道为反演重构阵列侧向测井曲线。

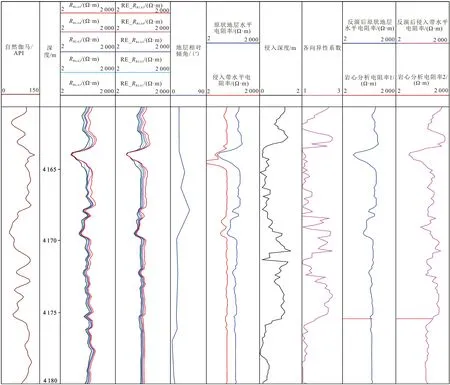
图11 阵列侧向测井资料解释结果

从实际测井曲线可以看出,井段4 162.5～4 164.0 m有明显的曲线分离现象,曲线分离因子最大达到2.627。由反演结果可以看出,该井段存在明显的钻井液侵入,侵入深度约为0.4～1.2 m,反演后的原状地层水平电阻率(约200 Ω·m)远大于反演后的侵入带水平电阻率(约30 Ω·m),从而对曲线的分离特性给出了合理性解释;其次,第四道表明,反演重构阵列侧向测井响应与实测曲线变化规律基本一致,验证了分级反演算法的有效性;最后,由第九道和第十道的岩心分析资料(红线)与各向异性电阻率反演结果的对比可以看出,两者一致性很高,进而验证了该方法的准确性和稳定性。

4 结 论

(1)钻井液侵入、各向异性以及地层倾角等因素能够使得阵列侧向测井不同探测模式曲线发生分离,其中钻井液侵入可致分离因子接近于10,影响最大,各向异性和地层倾角致其最大为1.2,影响程度远小于钻井液侵入。

(2)通过采用初值分级选取策略实现了反演参数初值的精确选取,精度范围达到0.2%～20%,满足初值选取需求,在此基础上,结合Levenberg-Marquardt反演算法提升了全局寻优能力以及收敛速度,比传统三维反演的速度提高近7倍。

(3)提出的分级快速反演方法能够实现中低阻地层(1～400 Ω·m)横向侵入剖面和纵向电阻率剖面的精确划分,且岩心分析数据与电阻率反演结果一致性高,进一步验证了该方法的准确性。