基于Logistic 方程的真菌对林木分解率的数学模型

陈星宇 王子琦 高晨阳 郭睿彤

（1、东北林业大学信息与计算机工程学院，黑龙江哈尔滨 150000 2、东北林业大学理学院，黑龙江哈尔滨 150000）

1 研究背景

真菌在碳循环中对植物物质和木质纤维的分解起着重要的作用。真菌活性包括生长速率和耐湿性，这两者对林木分解速率有直接的影响。此外，对于不同的林木类型，同一菌种的分解速率也存在差异。在实际的自然环境中，同一片区域有多种真菌存在，它们之间的种间竞争也对总分解率产生影响。因此，有必要对碳循环中的这一部分进行详细的分析。

2 基于Logistic 方程的真菌对林木分解率的数学模型建立

通过对真菌的生长速率、耐湿性以及不同林木类型的分析，建立将三个因素与总分解速率联系到一起的数学模型。由于不同菌株之间存在相互竞争作用，这对分解速率也有一定的影响。βi表示真菌竞争系数，用于反映真菌间相互竞争作用的强弱对总分解率所造成的影响。若变量因素相互独立，则时间序列各时期的发展水平为各影响因素之和，符合可加性模型。若变量间相互影响，则非独立，即时间序列的发展水平是多种因素共同作用的结果，符合可乘性模型。不同菌株生存在不同树种的环境中，对林木的分解率存在差异，且二者存在相关性，所以它们之间的关系是相乘的。同时，为了独立探究菌株内部相关因子（生长速率和耐湿性），分别添加了生长速率Grow-Decom 子模型和耐湿性Mois-Decom 子模型。

综上所述，基于Logistic 方程的真菌对林木分解率的总数学模型如公式（1）所示：

表1 总数学模型符号说明

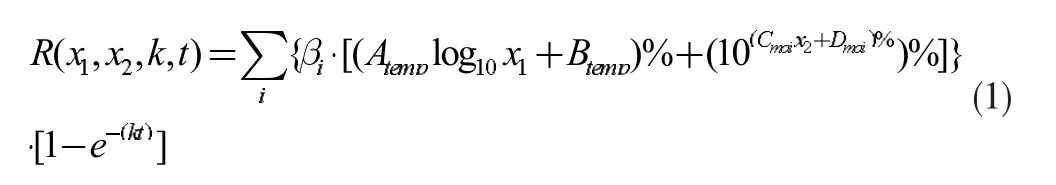
2.1 真菌的生长速率影响林木分解率的Grow-Decom 子模型

首先分析生长速率对分解率的影响并建立合适的模型：

其中R1(x)为真菌对林木枯枝落叶层和木材纤维的分解速率，x 为真菌的生长速率。

2.2 真菌的耐湿性影响林木分解率的Mois-Decom 子模型

真菌的耐湿性对分解率的影响可以采用表达式

去掉对数且化简得

其中x2代表真菌的耐湿性，R2（x）代表分解速率。

2.3 树种类型影响林木分解速率的Tree-Decom 子模型

树种也会影响真菌对木材的分解率。根据Olson 模型[1]可求出林木分解残留率为：

故可得分解率：

其中，k 为枯叶物腐解系数，与枯落物以及林木种类有关，t是分解时间。

3 数据模拟

根据资料[2]可查得黑龙江省大亮子河森林公园内八种白腐真菌的相关数据，基于已查得的真菌生长周期数据，本文依此对八种真菌的生长规律进行模拟，在计算机中基于此区间随机产生八种代号分别为A、B、C、D、E、F、G 的真菌生长周期数据，分别采用定性与定量的方法进行描述（此模拟数据及后续基于此数据的处理均仅用于验证本数学模型）。

根据资料[3]可查得Duddingtonia flagrans 分离株在两种相对湿度（35%与85%）、不同培养时间段（7 天至62 天）的产孢量的相关数据，基于已查得的此种真菌数据，本文依此种真菌在两种相对湿度下的产孢量进行模拟，仍然在计算机中基于此区间随机产生对应八种代号分别为A、B、C、D、E、F、G 的真菌在两种相对湿度下的产孢量数据（此模拟数据及后续基于此数据的处理均仅用于验证本数学模型）。在此数据的基础上，假定单位横截面积下真菌密度为1mg/mm，故可以将产孢量（以g·d-1作为计量单位）转换为产孢速率（即生长速率，以mm·d-1作为计量单位），结果如表2 所示。

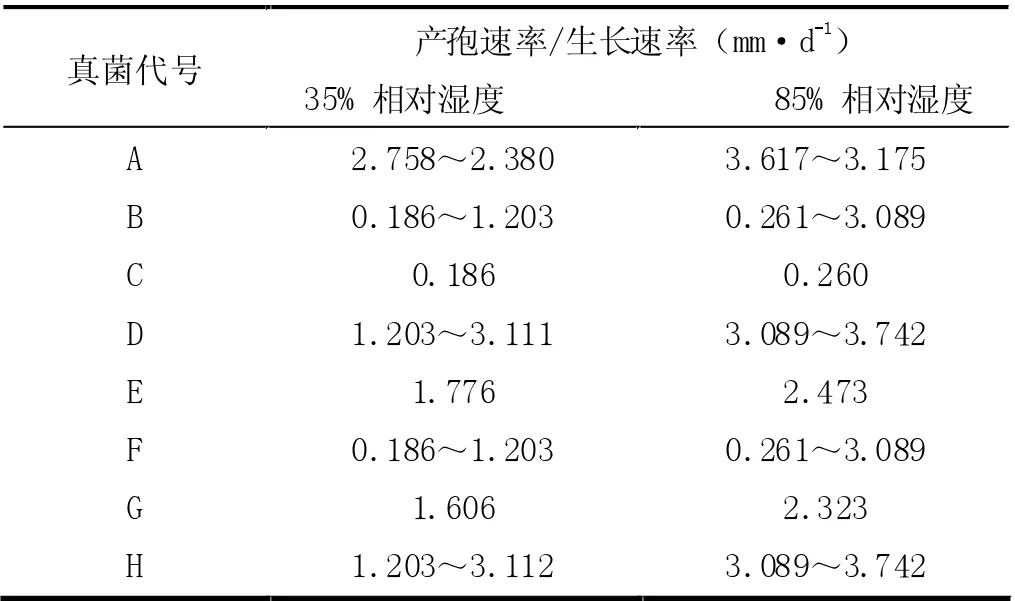
表2 真菌的产孢速率/生长速率

对随机产生的真菌产孢量模拟数据进行归一化处理，将数据映射到[-1,1]区间上，这样有利于简化后续建模中的运算。最终数据处理结果如表3 所示。

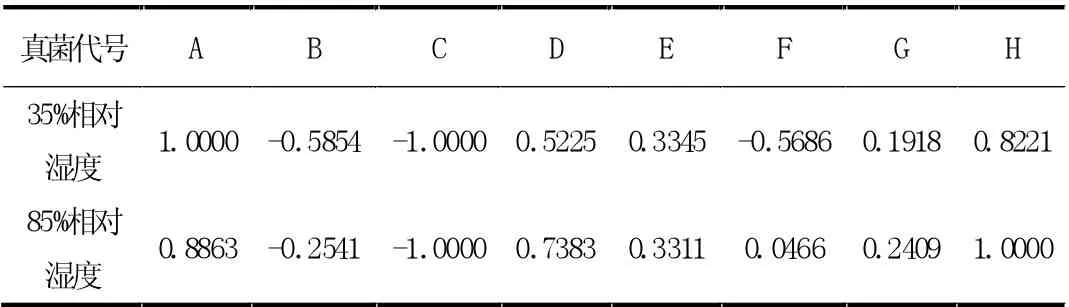
表3 最终数据处理结果

4 种间竞争的Logistic 方程与竞争系数

当存在两种真菌时，由种间竞争的Logistic 方程[4]，即式（7）、（8）：

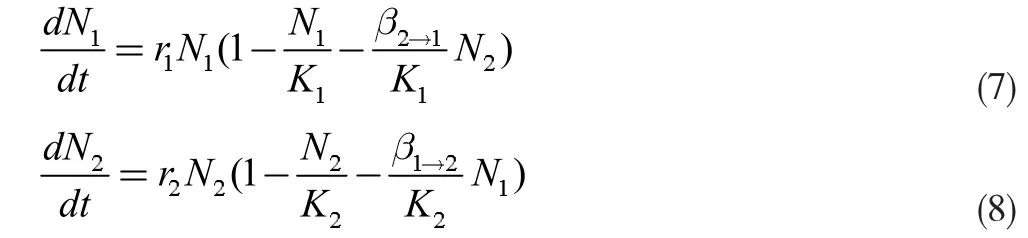
其中N1和N2分别为两菌种的种群数量，K1和K2分别为两菌种的环境容纳量，r1和r2分别为两菌种的增长率，β2→1为菌种种群2 对菌种种群1 的竞争系数，β1→2为菌种种群1 对菌种种群2 的竞争系数，可解出β2→1，如公式（9）所示，同理可得β1→2。

基于资料[3]的产孢量变化趋势，合理估计每种真菌的环境容纳量，结果如表4 所示。

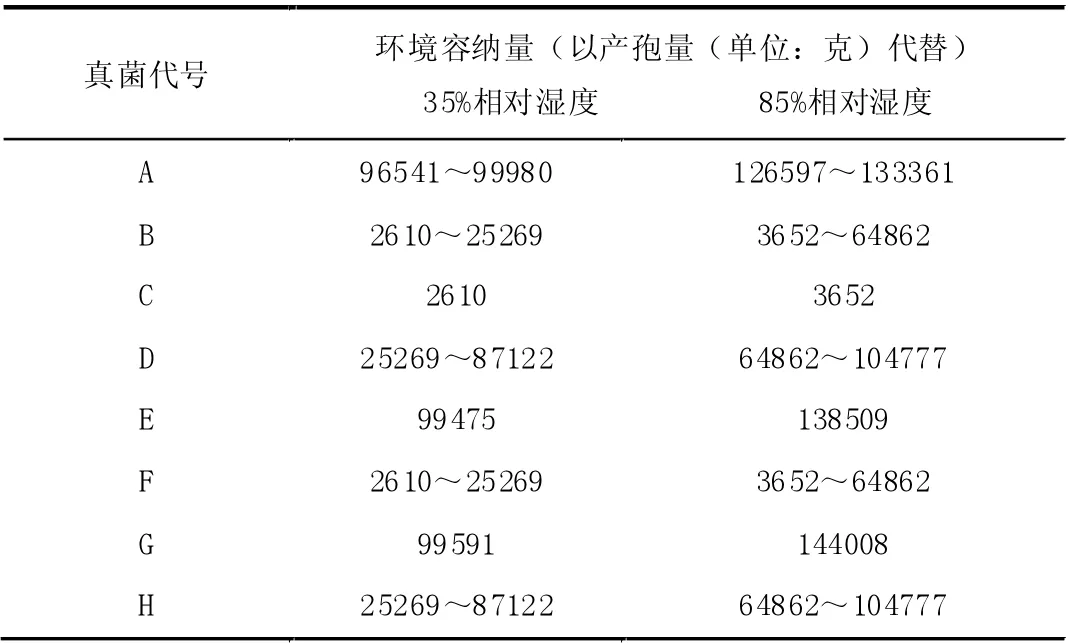
表4 每种真菌的环境容纳量估计值

5 不同类型真菌作用下的短期与长期趋势

短期趋势下，环境资源较为丰富，可以不考虑种间竞争的影响，问题就相当于考虑每个真菌种群单独存在时对分解率趋势的探讨。

长期趋势下，随着时间增加，总枯落物残余率逐渐变小。其中βi为不同种群的竞争因子，随着时间t 的变化，βi也会发生改变。一开始相对资源比较丰富，种间竞争影响较小，可忽略不计，此时每个真菌种群竞争因子βi都规定为1。当真菌数量达到一定积累量时，种间竞争的影响就更加显著。处于优势状态下的真菌的βi会更大，则该真菌对林木的分解速率影响就更显著。随时间推移，短期趋势下的优势种群可能不再在长期趋势下继续维持优势，而是竞争能力强的会在分解中占据主导地位，竞争能力弱的菌种数量可能越来越少。

6 不同自然环境下真菌对林木分解率的分析

不同环境下，真菌的分解能力也会受到影响。由于温度、湿度、物种多样性等因素的变化，就会改变真菌的生长速率和耐湿性，从而影响真菌对林木的分解率。针对热带雨林，其相对于其他环境而言，温度、湿度较大且自然资源丰富，此时对真菌的生长更有利，能大大提高枯枝落叶层和木质纤维的分解。而干旱和半干旱地区，相对于其它地区的环境更加恶劣，气候干燥且物种稀少，菌种生长所需的资源匮乏，全年高温与其他因素会同时抑制真菌的分解能力，不利于物质的分解。对于温带地区，它的气候条件是优于干旱地区，但稍逊于热带雨林。通过以上分析，真菌的分解率为：热带雨林＞温带＞半干旱＞干旱。

7 菌种的生物多样性对林木分解率的影响

对于单一菌种而言，其相对于多种菌种组合没有竞争，能让单个菌种的分解能力发挥到最大程度。但同时也由于物种多样性的下降，使得对枯枝落叶层和木质纤维的分解效率有所降低。而对于多种菌种组合而言，与单个菌种进行比较，其物种多样性丰富，有利于加快枯枝落叶层、木质纤维的分解和整个生态系统的循环。但如果种间斗争过于激烈，也可能会起到相反的作用，使得分解效率大大降低。

7.1 单一真菌种群存在下的林木分解率

对于单个菌种，不需要考虑菌种之间的竞争。在湿度为35%，温度为22 摄氏度的条件下，利用公式（2）与（4）求得的结果加和即为真菌相关分解速率，利用公式（6）可计算得树种相关分解速率，利用公式（1）中i 与βi均取1（即仅有单一菌种）时可求得八种真菌分别对刺槐（枯叶物腐解系数为0.490g/(g·a)）[3]的分解率，处理之后的结果如表5 所示。

表5 八种真菌对刺槐的分解率

7.2 两种真菌种群存在下的林木分解率

在湿度为35%，温度为22 摄氏度的条件下，将表5 中的八种真菌进行两两组合，利用公式（1）并结合公式（10）与表4 可计算两种真菌共同作用下新分解率，处理之后的结果如表6 所示。

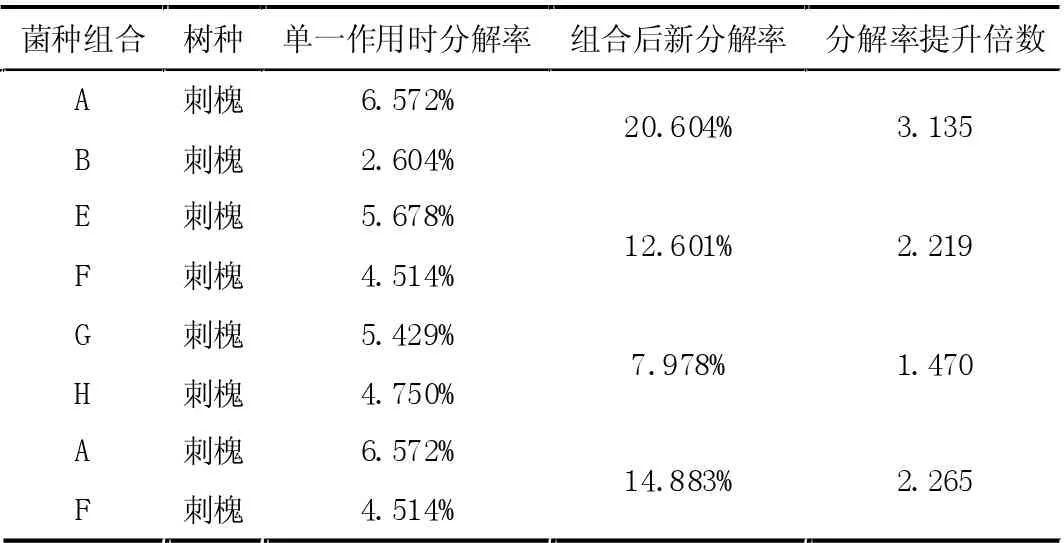
表6 两种真菌存在下新的分解率

8 模型结果分析

图1 菌种组合对分解率的促进作用

单个真菌种类的自身分解能力（Fungiself-decompositionrate）与林木种类相关的分解速率共同作用，得到在该种林木下不同的单一菌种的分解速率（Fungi-relateddecompositionrate）。随着真菌种类的增加，各菌种在共同作用下的新分解率（Newdecompositionrate）高于单个真菌种类的分解速率，如图1 所示。结果表明，真菌种群多样性与其分解速率呈正相关关系。

9 结论

9.1 在Olson 凋落物分解模型的基础上，研究了存在种间竞争时多种真菌联合作用对林木分解速率的数学模型。菌种的内部因素包括生长速率和耐湿性，树种因素影响枯叶分解系数。在总分解率的影响中，真菌种类与林木类型之间的影响服从乘法模型，真菌种类内部因素的影响服从加法模型，最后通过竞争系数进行组合。

9.2 短期趋势下问题简化为考虑每个种群单独存在时对分解率的探讨。长期趋势下，处于优势状态下的真菌的竞争能力越强，对林木的分解率影响就越大。在不同的自然环境下，由于温度、湿度、物种多样性等存在差异，真菌对林木的分解率由强至弱为：热带雨林＞温带＞半干旱＞干旱，即环境越利于菌落生存，分解率越大。在此模型中，生态系统的整体效率可用分解率来表征，通过对单菌种、双菌种的分解率进行比较，发现种群多样性越丰富，分解率越大，系统的整体效率越高。

9.3 本文所建立的数学模型不仅旨在用于分析解决菌种因素、树种、种间竞争等多种组合变化与林木分解率的关系，也可以推广用于研究除分解率外的其他环境指标及其影响因素之间的关系，以及其它多因素间存在相互牵制关系的非生物指标分析，如企业竞争力分析等。