潜标抗漂移布放技术
唐 松,米智楠,杨群慧,吴正伟,金 璐
(1. 同济大学 a. 机械与能源工程学院,上海 201804; b. 海洋与地球科学学院,上海 200092;2. 国家海底科学观测网大科学工程办公室,上海 200092)
0 引 言
海底科学观测系统是继地面与海面观测系统和空中遥测遥感系统之后建立的第三种地球科学观测平台,力求从海洋内部直接、细致地对海洋环境的各种参数进行观测。潜标作为重要的水下观测设备,在海洋科学研究中具有重要作用,能对水体剖面实现原位、长期、连续、实时、高分辨率和高精度观测。GOBAT等采用有限差分法建立了低张力海缆与海床相互作用的数学模型,并编写了一套锚系姿态计算软件。SEBASTIAO等基于离散的等效项近似模拟连续挠性原理,对缆索进行动态建模,得到了可快速自动检索电缆的动态模型的通用算法。采用合理的潜标定位布放技术能提高观测数据的准确性,相关研究已引起越来越多研究人员的重视。潜标入水之后,重块会在海流的影响下发生漂移,漂移的距离随着海水深度的增加而增大,导致潜标在水中的实际位置与入水时的经纬度存在差异。为得到潜标在水中的实际位置,有必要对其进行定位,以降低回收风险。王澍初等针对国内精准定位布放作业存在的问题,提出一种基于无人遥控潜水器(Remote Operated Vehicles, ROV)成像声呐图像构建海底平面坐标系的深水设备精准定点布放方法。周红伟等采用超短基线技术为水下调查设备提供精确的位置信息。孙万卿针对浅海水声定位技术的特点,基于有穷状态自动机理论对浅海声场进行建模,研究了有效声速法的水声定位算法。王琦等采用时差定位法和交会定位法解决双矢量潜标交会定位问题。陈经刚提出一种量化潜标三维运动的方法,将潜标分段之后,采用测量仪器确定每段线缆的倾斜方向,由压力和潜标布放参数确定其倾斜角度,以实现潜标各部分的空间定位。米智楠等对潜标浮力配置在布放潜标过程中的作用进行了探索。
国内外学者在潜标声学定位等方面做了有益的尝试,但在抗漂移定位方面开展的研究还比较少。本文在满足总浮力配置要求的前提下,从提高安全性的角度对比研究4种方案的抗漂移能力,为潜标的定位布放提供参考。
1 潜标坐标系
潜标由主浮体、系留缆索、仪器包组件(包括声通机和传感器组等)、机电系留缆(EM缆)和海床基组件(包括声学释放器、传感器组和沉底重块等)组成。传统的潜标全部通过系留缆索连接,只能实现非实时、低频科学数据采集;本文所述模型中的EM缆可连接多个传感器包,数据传输到海床基,海床基能通过缆系实时通信。采用集中质量法将潜标模型离散为一系列节点和无质量的弹簧,潜标的集中质量模型见图1。
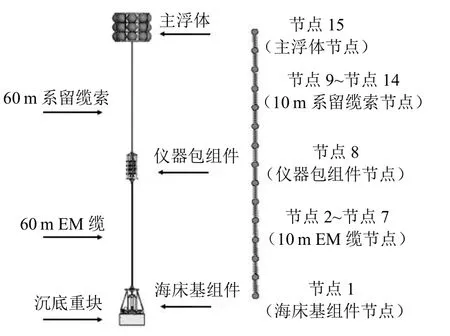
图1 潜标的集中质量模型
采用标锚法布放潜标,即逆着水流方向,依次放入主浮体、系留缆索、仪器包组件、EM缆和海床基组件。采用二维笛卡尔坐标系Oxy
,将y
轴定义为水深方向,将x
轴定义为海平面方向,将坐标原点O
定义在主浮体的质心上,得到布放简化示意见图2。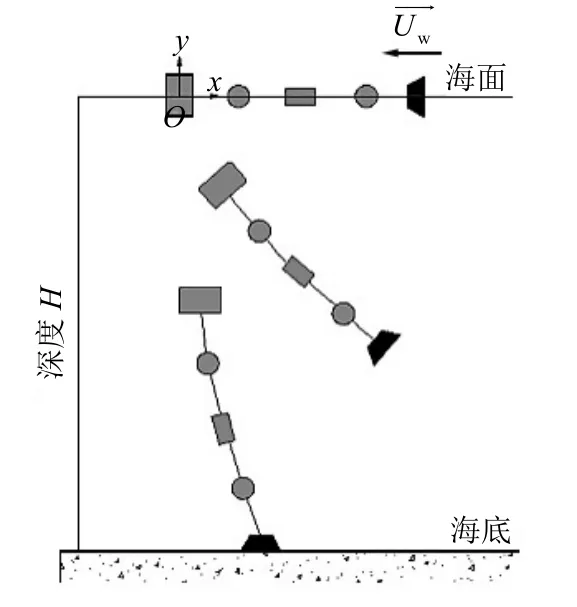
图2 标锚法布放简化示意
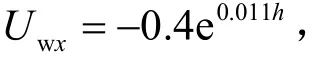
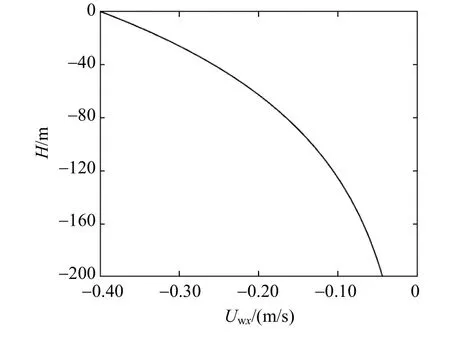
图3 海流速度分布函数
2 潜标的数学模型
潜标节点在运动过程中受到重力iG
、浮力iB
、水动力阻力F
、惯性力F
和缆索的张力iT
的作用,受力示意见图4,其中:v
为流体速度;v
为节点速度。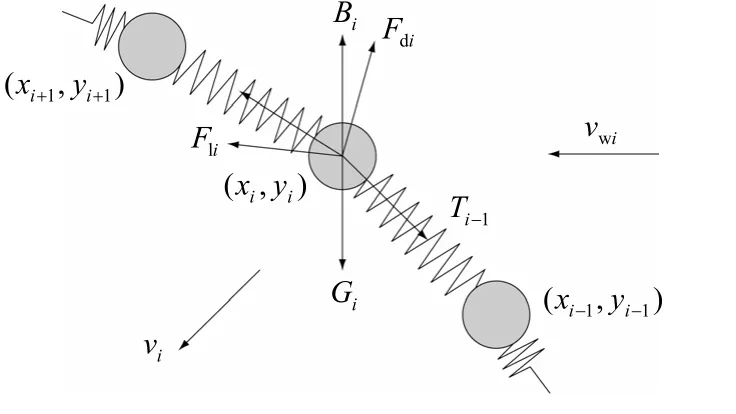
图4 节点在布放过程中受力示意
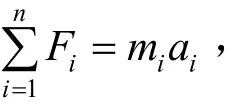

m
为节点i
的质量;a
为节点i
的加速度;f
为海床对潜标的作用力,触底时才会产生,故在受力图中未表示。2.1 浮力和重力
在布放潜标过程中,将重力视为定值,浮力可通过积分求得

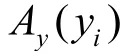
2.2 流体阻力
流体阻力的表达式为

C
为流体阻力系数;l
为节点之间的距离;d
为节点的直径。2.3 惯性力
节点所受惯性力由附加质量效应产生的部分和排开流体体积2部分组成,表示为

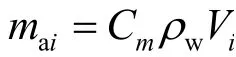
2.4 张力
节点所受张力示意见图5,1个单元的2个节点分别设为节点1和节点2。节点1和节点2受到的力分别为T
和T
,二者大小相等。取二维平面,可在x
方向和y
方向上投影。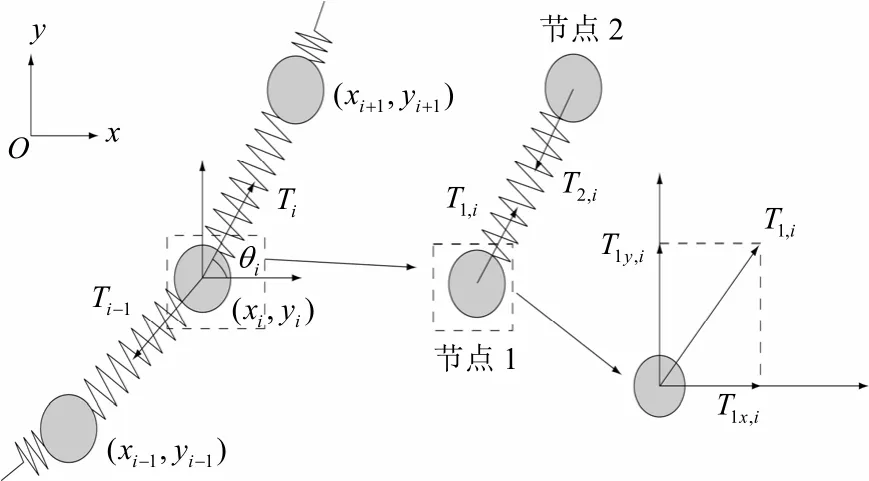
图5 节点所受张力示意
根据胡克定律,张力的计算式为
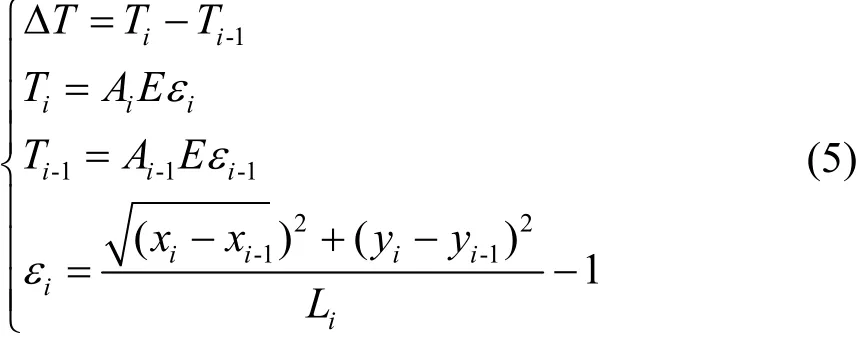
A
为节点i
的横截面积;E
为弹性模量;L
为缆索自由长度;ε
为布放过程中缆索的伸长量与自由长度的比值。2.5 海底作用力
潜标触底之后与海床的相互作用可参考GOBAT等和常洪波等的研究,将海底基当作线性阻尼系统求取。海底对潜标的支持力可表示为
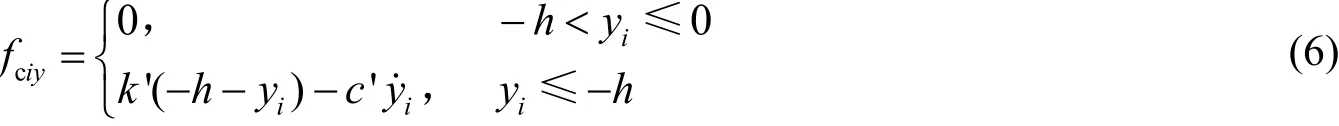
潜标受到的海底摩擦力为

μ
为摩擦因数;k
'为海底刚度系数;c
'为线性阻尼系数。根据上述公式可得到二阶非线性偏微分方程组,可采用Runge-Kutta法进行数值解算。通过MATLAB内置的 ODE45 函数对微分方程进行数值积分,可对潜标锚系进行水动力学分析。
3 数值模拟结果分析
3.1 仿真参数说明
EM缆和系留缆索的长度均为60m,每隔10m离散为1个节点,故可将潜标离散为15个节点。节点1为海床基节点,节点2~节点7为EM缆节点,节点8为仪器包节点,节点9~节点14为系留缆索节点,节点15为主浮体节点。上述公式用到的系数见表1和表2,附连质量系数C
和流体阻力系数C
参考BERTEAUX的描述,滑动摩擦因数参考孙雷等关于摩擦因数的描述,海底刚度系数k
'和线性阻尼系数c
'参考FEBER关于土壤等效刚度和阻尼的说明。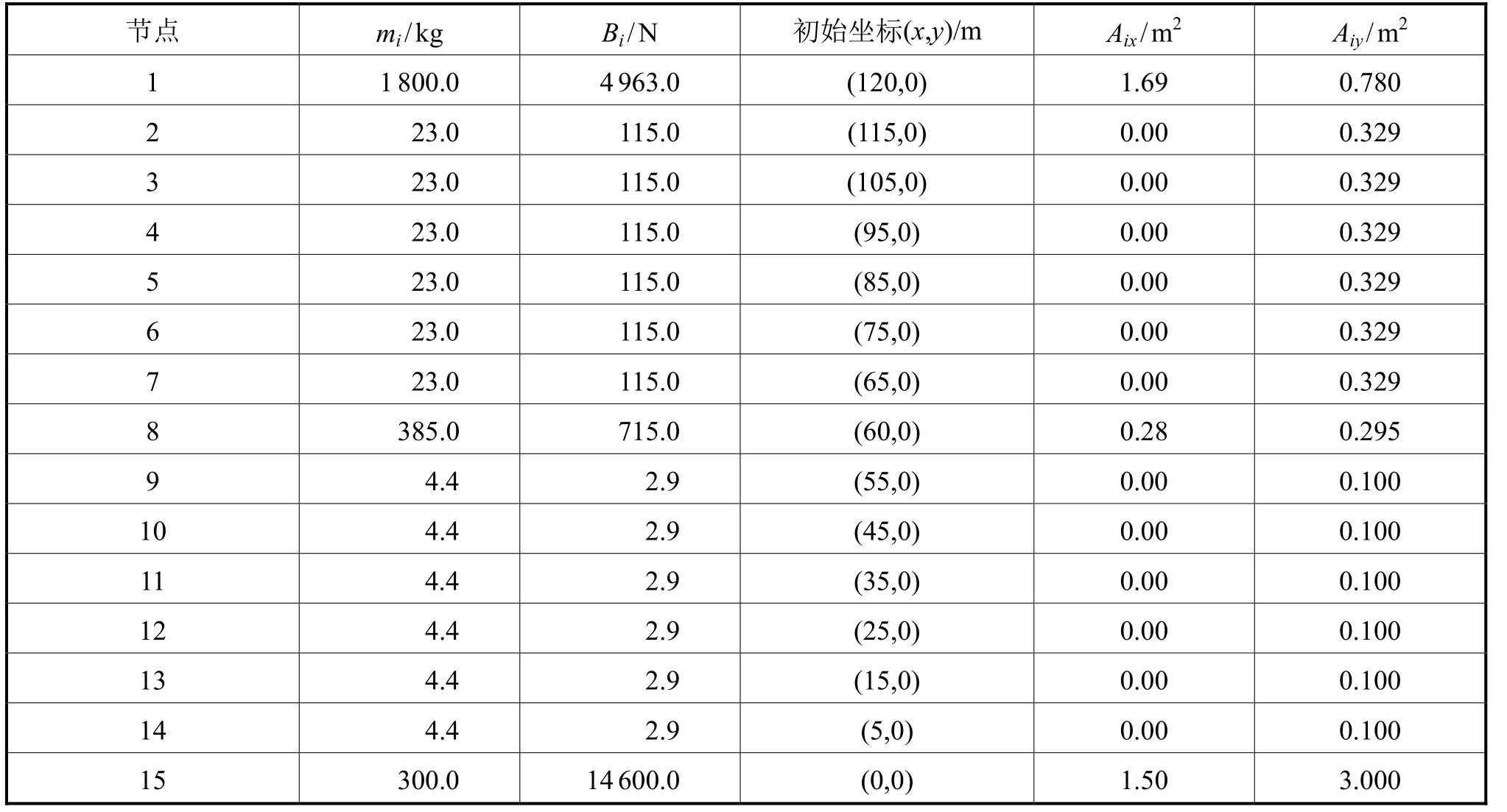
表1 各节点的物理参数

表2 潜标锚系水动力学参数
3.2 不同型式潜标水平方向运动对比
在满足总浮力需求的前提下,从提高抗漂移性能的角度出发,兼顾回收的可靠性、张力和着底冲击力的下降等,提出4种潜标方案(见图6),其中:方案1是对比研究的基础,不增加额外浮力;方案2是在海床基与仪器包之间增设浮力部件(小浮球组);方案3是在仪器包与主浮体之间增设浮力部件;方案4是在仪器包的上、下两端均配置浮力部件。由于增设了浮力部件,方案2和方案3相应增加1个离散节点(即1个小浮球组节点),方案4增加2个离散节点(即2个小浮球组节点)。
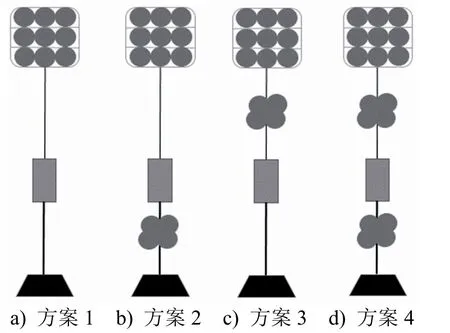
图6 4种潜标方案
潜标入水之后,各部件会在海床基(包括沉底重块)的作用下逐渐向中间靠拢,并在重力的作用下绷直、下降。选取海床基节点、仪器包节点和主浮体节点等3个关键部件,得到4种方案下各节点在水平方向上的漂移量见图7。
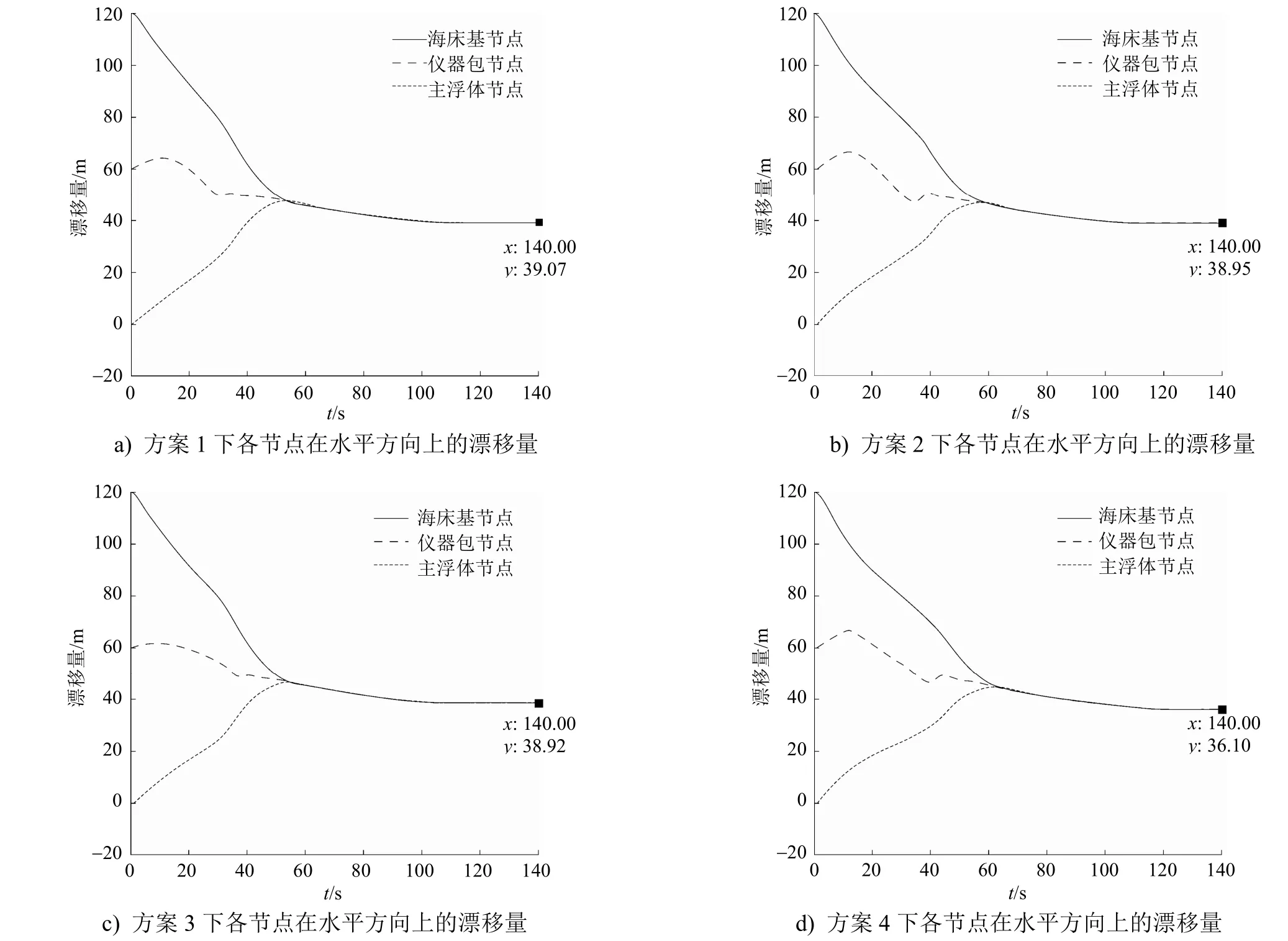
图7 4种方案下各节点在水平方向上的漂移量
图7中,数据游标显示值为海床基节点的最终落地点在水平方向上的坐标(x
,y
)。由图7可知:方案1~方案4的落地点纵坐标依次为39.07m、38.95m、38.92m和36.10m,而4种方案的初始纵坐标均为120m,因此方案1~方案4的海床基节点的漂移量分别为80.93m、81.05m、81.08m和83.90m;增加浮力部件(小浮球组)会使水平漂移量增大,对应方案2和方案3,二者的水平漂移量差别不大,说明浮力部件与安装位置关系不大。考虑到增加浮力部件会引起张力发生变化,选取海床基节点、仪器包节点和主浮体节点等3个关键部件,得到4种潜标关键部位的张力响应对比见图8。
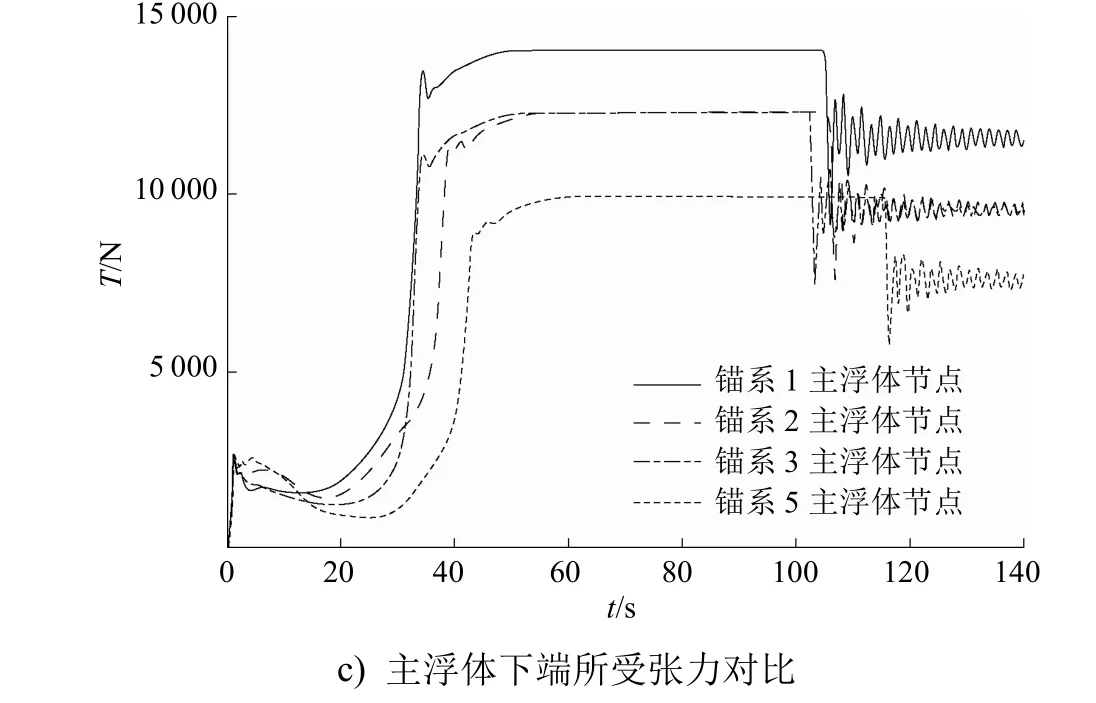
图8 4种潜标关键部件的张力响应对比
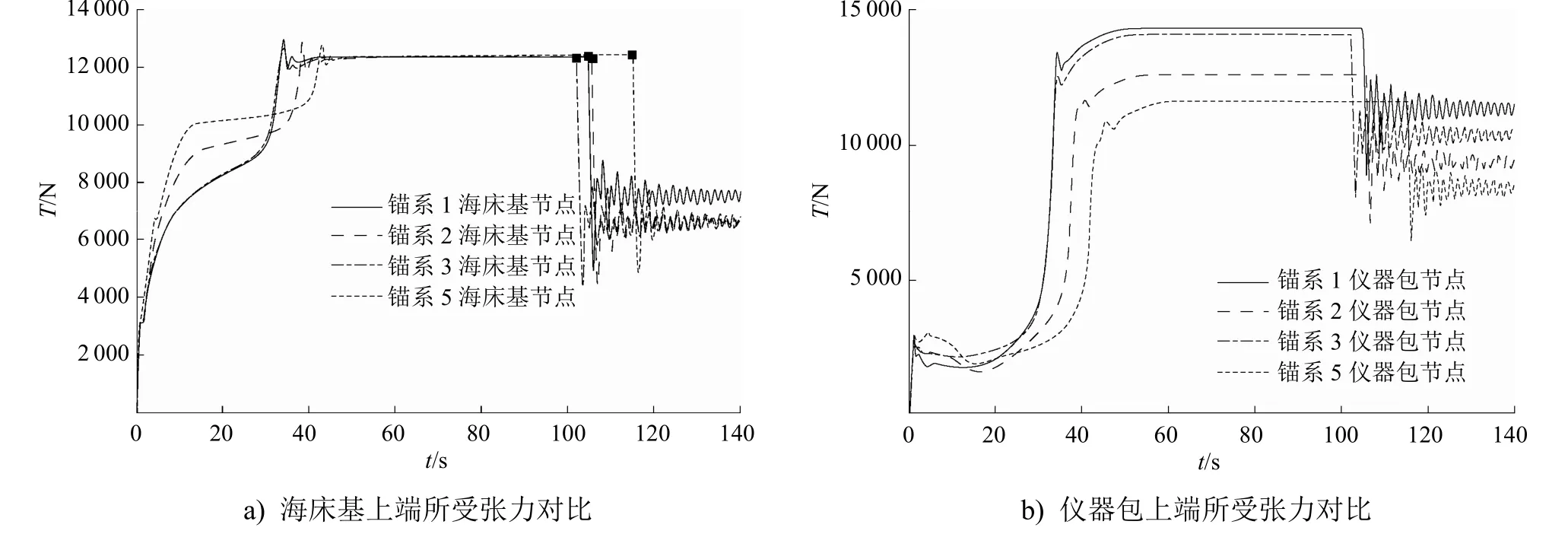
由图8可知:方案1~方案4的潜标触底时间依次为101.7s、104.4s、105.3s和114.7s,即随着浮力部件的增加,潜标触底时间变长;增加浮力部件对海床基上端所受张力的峰值几乎没有影响,但可降低其稳态张力;对于仪器包和主浮体,增加浮力结构可有效降低其张力峰值和稳态张力值。
3.3 海床底质环境的影响
海床底质可能为淤泥、沙质和岩石底质等。随着底质的逐渐密实,海床的刚度系数会逐渐增大。选择3种海床底质的刚度系数,即K
=10kN/m(底质1)、K
=20kN/m(底质2)、K
=40kN/m(底质3),研究海床底质对潜标布放运动的影响。图9为方案4在3种海床底质刚度系数下的张力变化情况。由图9可知:在3种海床底质刚度系数下,方案4的海床基节点所受峰值张力和稳态张力几乎是一样的,即不同刚度的海床底质对海床基节点的峰值张力和稳态张力几乎没有影响,这可能是由于在触底时海床基节点的张力已达到峰值;同时,在触底过程中,海床基触底会导致缆索松弛,并在浮力的作用下呈现张紧状态,即在触底过程中,缆索交替出现松弛、张紧现象。这种现象因海床底质刚度系数的不同而尤为明显;海床底质的刚度越大,振动幅度和频率越大。
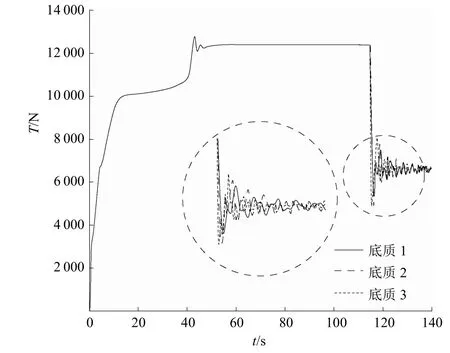
图9 方案4在3种海床底质刚度系数下的张力变化情况
3.4 海流速度的影响
在布放潜标过程中,海流速度也不尽相同,海流对潜标的作用主要体现为拖曳作用。下面考虑海流速度分别为U
=0(环境1)、U
=-0 .2e(环境2)和U
=-0 .4e(环境3)等3种情况,研究潜标的运动轨迹。以方案4为例,海床基节点在不同海流的作用下呈现出不同的漂移量(见图10)。图10中,数据游标显示值为稳态时,水平方向(x
方向)上的漂移量和铅垂方向(y
方向)上的运动量。由图10可知:当海流速度U
=-0 .4e时,潜标落地点坐标为(36.10, -200.3);当海流速度U
=-0 .2e时,潜 标 落 地 点 坐 标 为(47.81,-200.3);当海流速度U
= 0时,潜标落地点坐标为(60.35, -200.3);3种情况下潜标的水平漂移量分别为83.90m、72.19m和59.65m,即随着海流速度的减小,潜标的水平漂移量逐渐减小。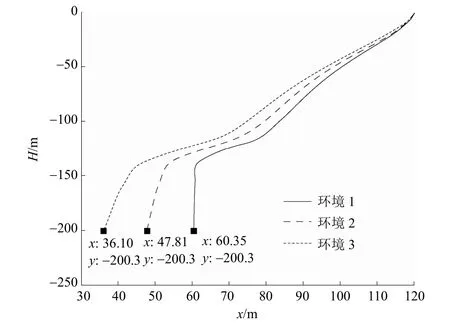
图10 不同流速下海床基节点的运动轨迹
4 结 语
本文采用集中质量法将潜标离散为多个集中质量节点与无质量弹簧连接,对潜标在布放过程中的受力情况进行分析,并编制MATLAB程序模拟分析4种配置的模型、3种刚度的海底底质和3种海流速度情形下潜标在布放过程中的漂移量和触底时间的变化情况,研究结果如下:
1) 在保证总浮力满足需求的前提下,适当在关键部位增加浮力部件有助于提高潜标回收的可靠性,但在布放潜标时会增加其水平漂移量,并在一定程度上延迟触底时间。浮力部件的安装位置对潜标水平漂移量的影响较小。
2) 海流速度对潜标漂移量的影响也需考虑,海流速度越大,潜标漂移量越大。因此,在布放潜标时需考虑当地海流的速度。
3) 3种海床底质条件对缆索的峰值张力和稳态张力的影响非常小,这可能是由于在潜标触底时各节点的张力已达到峰值。同时,在触底过程中,缆索交替出现松弛和张紧现象,海床底质的刚度越大,缆索的动态振动幅度和频率就越大。

