比例尺度和粗糙度影响下的溢洪道水流结构数值模拟

厉建阳

(蒙阴县水利局，山东 蒙阴 276000)

1 概 述

如果设计和建造得当，反弧型(OGEE)溢洪道能够高效和安全地通过水流，并且具有良好的测流能力[1]。OGEE溢洪道在设计水头的顶部产生接近大气压的压力，在水头低于设计水头时，由于波峰阻力流量较小，在水头较高的地方，流量较大[2]。当上游流动条件改变、峰形或由于局部几何特性引起的水流路径改变，可能会导致流动特性产生变化[3]。物理模型已被广泛用于分析尺度与粗糙度对溢洪道的影响。但物理模型的缺点是成本高，而且需要耗费相当长的时间才能得到结果[4]。此外，随着原型与模型尺寸之比的增加，尺度效应可能会引起的更大的误差。

计算流体力学程序FLOW-3D可以对溢洪道上的流动进行研究[5]。前人研究结果表明，物理模型和FLOW-3D数值模型中对压力和流量的模拟具有良好的一致性。故本文采用CFD软件中的FLOW-3D模型，详细研究了在模型比例尺和表面粗糙度影响下的溢洪道流量、水面、坝顶压力、流速和压力垂向分布等水流特性。本研究的主要目的是通过对计算结果的分析，定量研究比例尺和粗糙度对流动特性的影响。

2 理论背景

2.1 比例和粗糙度

水工实验通过缩小原型比例尺建造模型，可以复制许多自然水流系统中的流型，并评估水工建筑物的性能。该模型存在一个缺陷：实验室的尺度效应。随着原型与模型尺度之比的增加，尺度效应的影响也随之增加，会导致误差变大。尺度效应的产生主要是由于空间、模型的可构造性、仪器或测量方面的原因。一般情况下，水工建筑物的明渠水流恒定非均匀流特性可用下式表示：

(1)

式中Sw——水面坡度；

h——槽底坡度；

k——固体边界粗糙度；

v——流速；

g——重力加速度；

ν、ρ，σ——水的动力黏度、密度、表面张力。

式(1)可以令明渠水流恒定非均匀流特性在缩尺模型和原型之间保持不变，以恰当地再现复杂原型流态的特征。

在缩尺模型的流动特性过程中，由于水的性质没有被缩尺，从而影响了建模的精度。因此，小比例模型可能会无法模拟与流体特性(如黏度和表面张力)相关的力，从而表现出与原型不同的流动。此外，由于实验材料的限制，缩尺模型不能准确再现原型的相对粗糙度。

前人对水工模型比例尺的限制进行了研究，得出了一些结论。大坝溢洪道模型采用30～100的长度比例尺，坝顶上的模型水流深度应至少为75mm。表面的平均粗糙度可以通过实验确定。表1给出了几种用于建造水力学结构和缩尺模型材料的粗糙度。

表1 不同材料的粗糙度k

为了定量确定比例尺效应和粗糙度对模型结果的影响，可以对包括原型在内的一系列具有不同表面粗糙度的比例尺模型进行试验。但是，水工模型试验费用高、耗时长，而且要对数据进行详细测量，导致了很多困难。随着计算机技术的进步和CFD软件的开发，可以在节约时间和成本的前提下，对溢洪道的水流进行数值模拟研究。

2.2 OGEE溢洪道

图1给出了标准OGEE溢洪道的形状，其中：P是堰高；Hd是堰上的设计水头；H0为高程，是包括流速水头Hv的总水头。流量的经验方程式如下：

图1 标准OGEE溢洪道的形状

(2)

式中C——流量系数；

L——侧向波峰长度。

3 数值模拟

3.1 控制方程和计算方案

不可压缩流动的控制范围和连续性方程如下：

(3)

(4)

式中ui——x、y、z坐标系的xi方向上的速度；

t——时间；

Ai——在i方向上流动的分数区域；

Vf——每个单元中流体的体积分数；

ρ——密度；

p——静水压力；

gi——i方向上的重力；

fi——湍流模型的雷诺应力。

为了求解快速变化波峰上的流动，模型对自由面进行准确的跟踪是很重要的。在FLOW-3D中，自由面是根据流体体积(VOF)函数定义的，该函数表示流体所占据的分数的体积。湍流闭合采用RNG模型。RNG模型可以更准确地描述低强度湍流和具有强剪切区的流动。

流动区域被细分为由固定矩形单元组成的网格，每个单元格都有因变量。除速度外，所有变量都位于单元格的中心，速度位于单元格表面(交错网格排列)。通过在模型中定义流动单元的部分面积和部分体积，将曲面、墙边界或其他几何特征嵌入到网格中。

3.2 建立数值模型

建模区域的尺寸见图2，为了建模方便，用z方向代替了图1中向上的y方向。模型区尺寸为长7Hd、高3Hd。为了加快收敛到稳态解的速度，采用了手动多重网格法。初始粗网格可以快速计算出近似的水面和流量。然后，通过将先前计算的值内插到网格上来得到更精细的网格。

图2 建模区域的尺寸

为了研究尺度效应和粗糙度效应，采用了图3所示的六种情况。对研究粗糙度效应的PR00、PR05、PR30和研究尺度效应的PR05、M50、M100、M200进行了数值模拟。原型溢洪道一般为混凝土结构，因此将其糙率设定为0.5mm，用于分析粗糙度效应。通过式(1)对表面粗糙度为3.0mm的水力光滑表面进行了数值模拟，用来分析方程中与雷诺数有关的尺度效应，对1∶50、1∶100和1∶200比例模型进行了数值模拟，用来分析方程中与韦伯数有关的尺度效应。在缩放模型的建模中，网格分辨率与原型的建模保持一致。

图3 模型分类情况

3.3 边界条件

本文设定了以下几类边界条件：上游静水压力；下游出流；无滑移作用；底部下游出流。在这种情况下，水流在底板和堰与顶部的大气压力边界之间从左向右移动。无滑移作用的定义是水流切向滑移速度为零。由式(2)确定上游高程水头和进场速度水头。将不考虑壁面摩擦能量损失的上游边界条件列于表2。

表2 上游边界条件和建模时间

4 结 果

4.1 溢洪道泄洪流量

表3给出了几种粗糙度下溢洪道上的单宽流量。根据表1，混凝土的实际粗糙度约为0.1～3.0mm，因此对表面粗糙度为水力光滑、k=0.5mm、k=3mm的混凝土进行了数值模拟，并对模拟结果进行了分析。水位流量关系[式(2)]的计算结果表明，流量随表面粗糙度的增加而略有下降。粗糙度对最大流量的最大减少率仅为0.4%左右。

表3 几种表面粗糙度下溢洪道的泄洪流量

表4给出了几种模型比例尺下的单宽流量。原型的表面粗糙度取0.5mm，根据几何相似度对不同比例尺模型的表面粗糙度进行了调整。为了排除不同尺度网格中产生的数值误差，对原型和缩比模型的网格也进行了几何相似性调整。水位流量关系的计算结果表明，随着模型与原型长度比例的增加，流量略有下降。1∶200比例模型最大流量的减少率仅为0.6%左右。这表明，从流量的角度看，由于尺度变化引起的雷诺数畸变可以忽略不计。

表4 几种比例尺下溢洪道的泄洪流量

4.2 溢洪道上的水面模拟

图4中描绘了三种不同水头下的溢洪道水面，并给出了WES堰的试验数据作为对比。图4(a)给出了溢洪道上水力光滑表面(PR00)和表面粗糙度k=3mm(PR30)的水面。图4(b)显示了原型(PR05)和1∶200比例模型(M200)溢洪道上的水面。结果表明，随着表面粗糙度和模型比例尺的变化，水面波动幅度很小。如果仅仅采用混凝土的一般粗糙度，则表面粗糙度引起的数值误差不大。

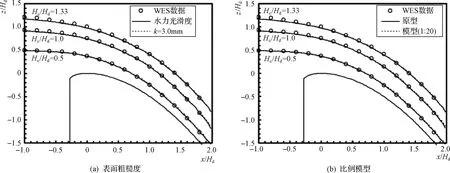
图4 溢洪道上的水面

4.3 溢洪道坝顶的压力分布

三种不同水头下溢洪道顶部的压力分布见图5，其中Hp为压力水头。图5(a)描述了水力光滑表面(PR00)和表面粗糙度k=3mm(PR30)时溢洪道上的顶部压力。图5(b)显示了原型(PR05)和1∶200比例模型(M200)溢洪道上的顶部压力分布。结果表明，数值模拟的压力分布结果与和实验结果基本一致。随着表面粗糙度和模型比例尺的变化，波峰压力变化不大。

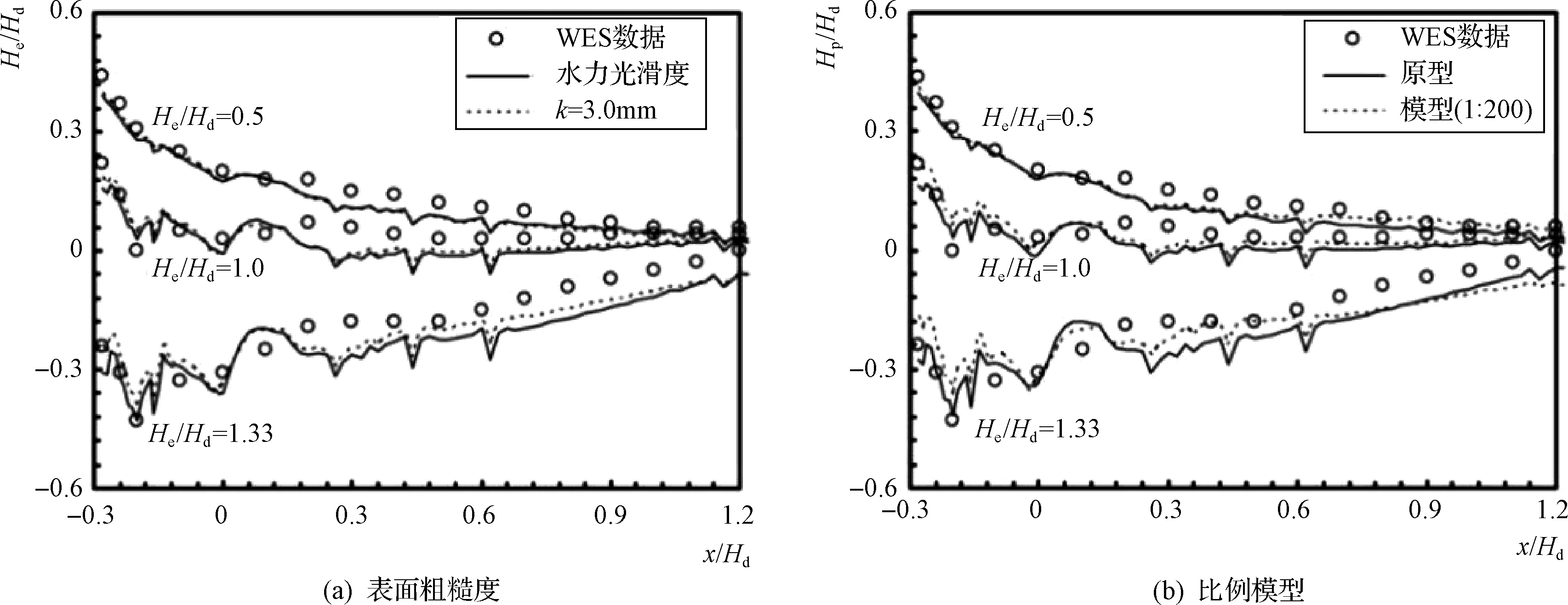
图5 洪道坝顶压力分析

4.4 速度的垂直分布

当He/Hd=1.33时，溢洪道顶部流速的垂直分布见图6，其中vmax为任意截面的最大流速。

图6 速度的垂直分布(He/Hd=1.33)

图6(a)描绘了水力光滑表面(PR00)和表面粗糙度k=3mm(PR30)时溢洪道上的流速垂直分布。在该图中可以观察到水力光滑表面的主要流动特性。底层水流首先在溢洪道前缘加速，自由面水流通过坝顶轴线后逐渐加速。最后，流量演化为对数分布。在流速vmax最大的位置低于垂线位置处，光滑表面的流速大于粗糙表面的流速。在上部，光滑表面的流速小于粗糙表面的流速。图6(b)显示了原型(PR05)和1∶200比例模型(M200)溢洪道上的流速垂直分布。如果选择百米作为参照点，则在参照点以下，原型的速度大于比例模型的速度，但在参照点以上，原型的速度小于比例模型的速度。

He/Hd=1.0和0.5的速度分布见图7和图8，流速分布的总体趋势与图6基本相同，但经过峰值后，随着上游水头的降低，流速更快地演化为对数分布。

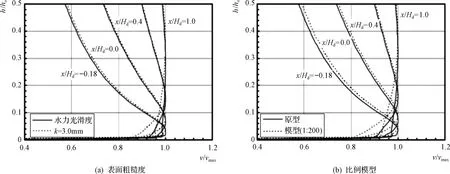
图7 速度的垂直分布(He/Hd=1.0)

图8 速度的垂直分布(He/Hd=0.5)

4.5 压头的垂直分布

当He/Hd=1.33时，溢洪道顶部压力水头的垂直分布见图9。

图9 压头的垂直分布(He/Hd=1.33)

图9(a)描绘了水力光滑表面(PR00)和表面粗糙度k=3mm(PR30)的溢洪道上压力水头的垂直分布。在坝顶轴线上游，随着水深的增加，压力分布与静水压力分布有一定的相似之处，随着水深的增加，压力迅速减小为负压。在坝顶轴线下游，当溢洪道坝顶压力接近大气压时，各深度的压力分布与大气压基本一致。图9(b)显示了原型(PR05)和1∶200比例模型(M200)溢洪道上的压力分布。结果与图9(a)几乎相同。

图10和图11分别描绘了He/Hd=1.0和0.5的压力分布总体趋势，与图9几乎相同。

图10 压头的垂直分布(He/Hd=1.0)

图11 压头的垂直分布(He/Hd=0.5)

4.6 最大速度及其垂直位置

图12(a)描述了水力光滑表面(PR00)和表面粗糙度k=3mm(PR30)下的最大速度。随着表面粗糙度的增加，最大速度略有降低。图12(b)显示了原型(PR05)和1∶200比例模型(M200)沿x轴的最大速度分布,最大速度在比例模型上比在原型上小。最大速度出现在He/Hd=0.5、1.0和1.33时的垂直位置见图13。随着上游水头的增加，出现最大流速的垂直位置较低的情况，并且该位置是随着距离溢洪道前沿的距离增加的。

图12 最大流速分布

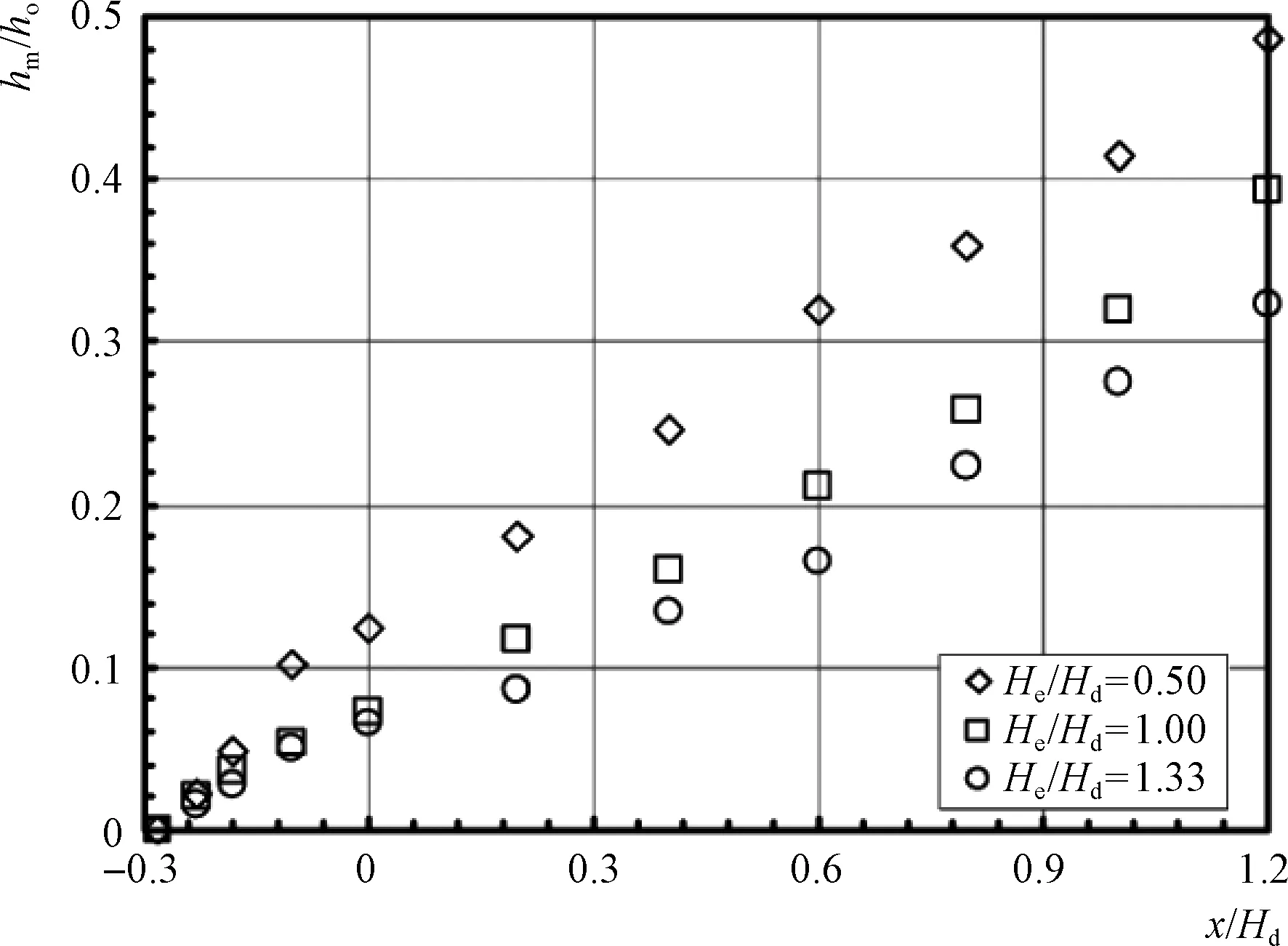
图13 出现最大速度的垂直位置

5 结 论

本文利用FLOW-3D模型，详细研究了模型比例尺和表面粗糙度影响下的溢洪道流量、水面、峰压等水流特性，以及流速和压力的垂向分布。结果表明：流量随地表粗糙度和模型比例的增加而减小，随着表面粗糙度和模型比例尺的变化，水面波动可以忽略不

计；在表面粗糙度和模型比例尺改变的情况下，溢洪道坝顶压力也会不同，但是，无论表面粗糙度和模型比例尺如何，垂直压力分布几乎是相同的；随着表面粗糙度和比例尺的增大，任意断面的最大流速均略有降低，最大流速出现的垂直位置随着距离溢洪道前沿的距离增加而增加。