运行工况下弧形钢闸门不同底缘型式对比优化研究

盖浩瑞

(莱阳市勘察工程队， 山东 烟台 265200)

1 工程背景

某水库是一座兼有防洪、灌溉、供水、养殖等诸多功能的大型骨干水库，水库大坝为混凝土重力坝坝型设计，主要由挡水坝段、溢流坝段和电站坝段组成。其中，溢流坝段顶部高程为87.8m，顶部宽度1.5m，溢流堰高程67.5m。溢流坝闸门为高19.7m，宽度为14.0m的弧形钢闸门。闸门的面板厚度为26mm。为了提高闸门的刚度和整体性，闸门的梁系采用实腹式等高连接和降低连接，其结构材料为Q235B钢材，弹性模量为206GPa，重度为78.5 kN/m3，泊松比为0.3。显然，弧形闸门在泄水过程中，其底缘部分会起到十分关键的作用，对流态和压强产生十分明显的影响，而不当的底缘设计则会对闸门的正常运行不利[1]。基于此，此次研究力求通过数值模拟的方法，进行不同底缘型式的对比研究，以获取最佳的底缘型式设计方案。

2 ANSYS有限元模型

2.1 有限元模型的构建

结合研究对象的特点和研究需要，对常用的有限元软件进行对比分析，确定采用ANSYS有限元软件进行计算模型的构建。该软件提供了直接建模、几何建模以及混合建模三种不同的建模方式[2]。其中，几何建模可使用多种几何图素，支持组合运算、布尔运算等多种有限元模型不能直接实现的操作，修改几何参数、网格密度和单元类型十分方便，适合3D实体结构和多方案对比研究，因此采用该建模方法[3]。

由于此次研究针对闸门开启运行工况下的水力特征对比研究，因此设定模型的计算范围为闸门的上游200m，下游100m。模型的高度为40m。鉴于弧形钢闸门的形状特点，采用柱面坐标系进行几何建模[4]。具体顺序为：首先建立一条闸门面板曲线，在建立的曲线上找到横梁的位置，也就是按照横梁间的弧线进行分段处理；然后，根据纵梁和面板曲线的垂直间距，利用已知曲线生成所有的纵梁，连接纵梁的关键点即生成所有的横梁以及面板的顶轮廓线和底轮廓线；最后，由左右两条曲线的边和顶轮廓线及底轮廓线形成面，也就是弧形钢闸门的面板，确定支臂的铰点坐标，其与主横梁、纵梁交点的连线即为支臂[5]。

由于弧形钢闸门的面板厚度较小，因此存在十分明显的几何非线性效应，而钢材本身也是一种典型的塑性材料。因此，在模型单元划分过程中，闸门的门叶和支臂全部离散为板壳单元，利用Shell63 模拟[6]。模型的其余部分则使用 Solid45 单元模拟。经过有限元网格划分，整个模型结构离散成 14154 个单元、13426 个节点，其中，弧形钢闸门的有限元模型示意图如图1所示。

图1 弧形钢闸门三维有限元模型示意图

2.2 计算荷载与边界条件

模型计算的边界条件设置为：将模拟计算区域的进口设置为速度进口，出口边界设置为压力边界条件，闸门部位的侧壁和底板设定为无滑移固体边界条件，上部与空气接触的顶面设置为对称面。结合相关研究成果，模型底板和边墙的糙率设定为0.008。结合工程的实际设计参数，研究中针对闸门开度6.0m，流量160m3/s的最不利工况进行计算分析。

2.3 计算方案

结合工程实际和前人的研究成果，设计了平底底缘(方案1)；倾角为45°的前倾式底缘(方案2)；倾角为45°的后倾式底缘(方案3)3种地缘设计型式，进行数值模拟分析，对比分析不同方案下的水深、时均压强和脉动压强，以获得最佳设计方案。

3 计算结果与分析

3.1 水深

针对3种不同的底缘设计方案，利用构建的有限元模型，对钢闸门运行工况下的上下游水位高度进行模拟计算，根据计算结果，绘制出的闸门上下游水位变化曲线如图2所示。由图2可知，在其他条件相同时，3种方案的弧形钢闸门上下游水深的变化规律基本一致，闸前水流平稳推进，在到达闸门时由于受到阻挡作用，呈现出一定的水面雍高，在经过闸门之后，水位高度迅速降低并逐渐趋于平稳。从水位的上下游差来看，水位差最大的为方案3，其次为方案1，最小的为方案2。同时，方案1和方案3的闸前水流波动性比较明显，说明水流流态相对不佳，而方案2的闸前水流波动性最小，说明水流流态良好。总之，钢闸门采用前倾式底缘设计时，上下游的水位差最小，且水流比较平顺，流态良好，对闸门的安全运行最为有利。

图2 不同方案上下游水深变化曲线

3.2 面板时均压强

针对3种不同的底缘设计方案，利用构建的有限元模型，对钢闸门运行工况下的面板时均压强进行模拟计算，在计算结果中选择7个关键测点，绘制出的面板时均压强变化曲线如图3所示。测点均位于上游面板，在闸门面板的中线由下向上布置，其中，每两个测点之间的弧面距离均为3m。由图3可知，在其他条件相同时，弧形钢闸门面板的时均压强呈现出由底缘向上部逐渐减小的变化特点。从不同计算方案的对比来看，方案3相同高程部位的时均压强值最大，方案1次之，方案2最小。由于不同计算方案在其他条件相同时的闸前水深不同，而时均压强又和闸前水深有密切的关系。因此时均压强值的大小与闸前水深的大小之间存在相同的变化特点。总之，方案2条件下的闸门面板时均压强值最低，且变化比较稳定，为3种计算方案中的最佳方案。

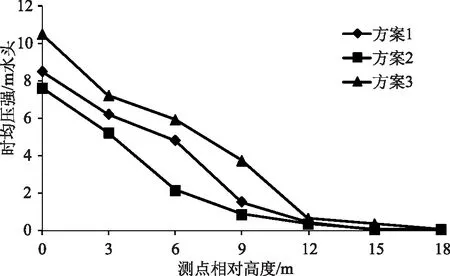
图3 面板时均压强变化曲线

3.3 脉动压强

脉动压强是水工建筑物水力学特征研究领域的重要问题，此次研究中选择与时均压强相同的测点位置，从数值计算结果中选择各个典型点位的脉动压强计算结果，绘制出的脉动压强变化曲线如图4所示。由图4可知，3种不同计算方案下的脉动压强呈现出类似的变化规律，均为0m测点部位的脉动压强较大，然后随着高程的增加，脉动压强值也不断减小，在达到水面高度部位时，脉动压强值又有所增大，然后进一步减小为0。究其原因，主要是水面部位由于受到闸门的阻水作用，水流产生明显的波涌，对闸门面板产生拍打现象。由于方案3的水面流态不佳，水流在闸门前的雍高现象比较明显，因此对闸门的拍打现象也比较剧烈，因此造成该方案下的脉动压强值在水面部位较大。总之，从脉动压强计算结果来看，方案2的脉动压强值相对较小且变化比较平稳，对闸门运行的安全稳定最为有利。

图4 脉动压强变化曲线

4 结语

目前，关于闸门底缘型式的问题，业界学者进行了诸多研究和探索，同时也给出了一些具体的研究成果和工程设计建议，但是当前的大部分研究以平面钢闸门为例。本次研究主要针对弧形钢闸门的底缘型式展开，研究了不同底缘型式对闸门水力特征的影响。研究结果显示，后倾角低缘型式下，闸门上游的水位雍高较大，水流流态不平稳，会产生比较严重的拍打面板现象，不利于闸门的安全运行。前倾角底缘型式下，闸门上游的水位雍高最小，水流流态最为平稳，对闸门的安全运行最为有利，而平底底缘设计则介于上述两者之间，因此在工程设计中建议采用前倾角底缘型式，至于倾角角度大小的影响，需要在后续研究中予以进一步的讨论和分析。