钻杆轴向运动对水平井段岩屑床的清洗效果

孙晓峰 毛 宁 鞠国帅 胡乔波 孙铭浩 于福锐

东北石油大学石油工程学院

0 引言

水平井、大位移井钻井过程中面临的一大难题就是如何保证大斜度和水平井段钻进时井眼足够的清洁，如井眼清洁不充分，就有可能导致许多钻井问题，如卡钻、托压、掩埋井眼等。钻井液携屑是典型的固液两相流动，影响钻井液携屑效率的因素较多，按照作用源分类，一是受循环介质（钻井液等[1]）运动影响，二是机械运动影响，如钻杆旋转[2-8]、横向运动[9]、轴向运动、高频震动以及携屑工具叶片旋转[10-17]等。

为了深入了解岩屑运移机理和岩屑床分布规律，众多学者已经开展了相当多的有针对性研究。郭晓乐等[18]根据固液两相流理论研究了岩屑的不同运移方式，综合考虑了岩屑分层和滑动运移方式以及钻杆旋转对岩屑运输的影响，建立了大位移井段三层岩屑动态运移模型。陈锋等[19]针对水平井和大斜度井岩屑携带困难设计了高效岩屑清除钻杆（EHCDP），其螺旋槽道结构使环空流体形成涡流结构，涡流的卷吸和钻杆旋转离心力可将岩屑甩入环空高边提高岩屑清洁效率。Zhu等[20]建立了水平井段岩屑三维瞬态模型，模拟了岩屑床层的分布特征及岩屑运移机理，模拟结果表明钻井工具能在一定程度上有效防止和主动破环岩屑床。蒋世全等[21]针对水平井大位移井钻井遇到的技术难题进行了摩阻—扭矩预测及评价、井眼净化等一系列研究，研究发现倒划眼及短起下钻过程中震动筛出口处会有大量的岩屑返出，证明短起下钻及倒划眼对岩屑运移和井眼净化有积极作用。Leising等[22]指出在连续油管钻井作业中通常使用高黏度的钻井液清洁环空中的岩屑，但他们发现这种方法只对悬浮层的岩屑有作用，而对已经形成的岩屑床必须要结合短起下钻通过钻头的旋转和轴向运动才能破坏岩屑床。张顺元等[23]认为短起下钻只能消除起下钻所覆盖的钻进井段中的岩屑床层，但当恢复钻进时，岩屑床高度将重新上升至原始状态，岩屑床并没有受到短起的影响。

目前钻杆做旋转对岩屑运移影响的模型、理论研究比较充分，但对于短起或倒划眼钻具对岩屑运移的影响则存在着不同的观点。因此，笔者将短起下或倒划眼运动抽象为钻杆的轴向运动，采用CFD数值模拟方法研究钻杆轴向运动对岩屑床破坏作用、岩屑运移的作用机制：首先讨论研究了短起下钻时钻杆接头外形的突变对岩屑运移的影响规律；其次评价了钻杆轴向运动速度、钻井液黏度对环空岩屑运移及分布规律的影响；最后根据模拟结果分析钻杆轴向运动是否有利于井眼清洁。

1 数值模拟

本文采用欧拉双流体模型研究钻杆轴向运动对水平井段环空固液流动的影响规律，欧拉—欧拉方法将颗粒相和液相作为连续介质，在计算量上比欧拉—拉格朗日方法节约计算资源，并且在工程上也被广泛认可。Realizablek-ε模型满足对应力的约束条件，可以在雷诺应力上与真实的湍流保持一致，故采用Realizablek-ε湍流模型解释流动过程中所涉及到的湍流现象。

1.1 控制方程

钻井液和岩屑的连续性方程可以表示为：

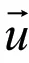
钻井液和岩屑的动量方程可以描述为：

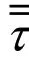
固体和液体之间的动量交换系数关系如下：

如果当αl≤0.8时：

当αl＞0.8时，流体和固体颗粒之间的交换系数计算方法为：

式中CD为阻力系数。

目前常用的阻力模型有Syamlal-O'Brien模型[24]、Wen&Yu模型[25]和Gidaspow模型[26]，其中Gidaspow模型是最常用的，具有很好的预测精度[27-31]。

当Res≤1 000时：

当Res＞1 000时：

式中颗粒雷诺数Res可以定义为：

式中ds为颗粒直径，m。

各相应力张量可以表示为：

固相压力ps可以定义为：

式中e是颗粒碰撞的恢复系数；Θs是颗粒温度，m2/s2；g0是径向分布函数，可以表示为：

固相的剪切黏度可以表示为：

固相体积黏度是颗粒对自己本身压缩和膨胀的阻力可以表示为：

对于分离流、涉及高压梯度的边界层流和具有复杂流动结构的流动计算，Realizablek-ε模型比标准k-ε模型具有一定的优势。在Realizablek-ε模型中，湍流动能（k）及其耗散率（ε）的传输方程如下：

式中σk和σs分别表示以上方程的普朗特数；C1、C2表示常数；Gk表示由平均速度梯度而产生的湍动能，其计算公式如下：

式中Cμ表示与平均变化率和湍流流场有关的函数；S表示应变张量平均速率的模量。

S定义如下：

以上公式在Realizablek-ε模型中出现的系数有：

1.2 几何模型和边界条件

综合考虑了计算资源和井眼实际工况，模拟采用的钻杆、环空几何尺寸，钻杆的运动速度、钻井液的流变参数等，如表1所示。

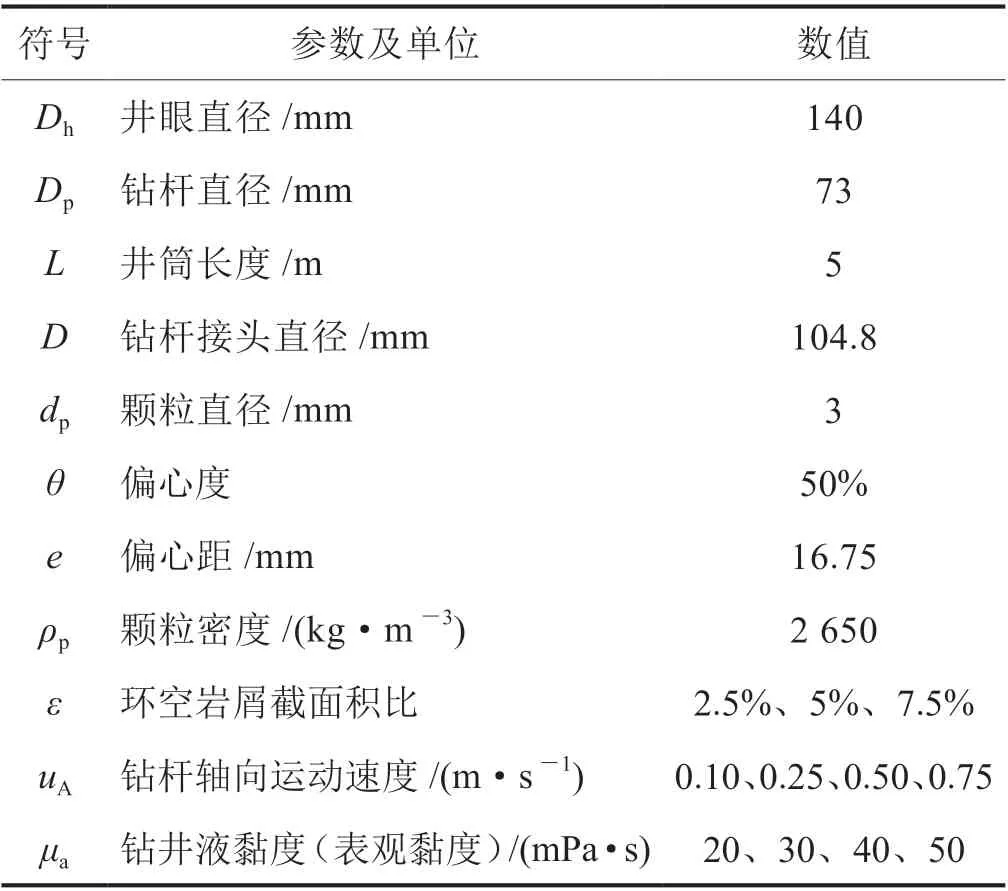
表1 模拟参数表

CFD数值模拟边界条件采用压力入口和压力出口，壁面采用无滑移条件，钻杆运动区域应用动网格实现钻杆轴向运动。求解时，控制方程采用有限体积法离散，压力—速度耦合采用相耦合SIMPLE格式离散，由于动量方程在六面体网格上表现良好，因此采用QUICK格式进行离散。通过对每个标度残差分量使用10－5的收敛准则来指定两个连续迭代之间的相对误差。选择0.000 1 s的时间步长，每个时间步长有20次迭代，模拟工作由28台Quanta T41S-2U服务器开展，单机配置CPU：intel E5-2680-V4 24核心，16G RDIMM，累计模拟时长约30天。

2 网格与模型检验

2.1 网格独立性检验

为提高数值模拟的精度，在钻杆起钻速度0.75 m/s的初始条件下开展网格独立性检验，本模拟中测试了4种网格数量对模拟精度的影响规律。表2显示了起钻速度为0.75 m/s时4种不同网格数量的模拟结果，以网格数量722 083作为网格独立性检验的初始值，网格数量依次从802 341增加到923 460，并再增加到1 005 600时，它们的预测值已经非常接近，这表明在给定的网划分中模拟结果几乎不随网格数量的增加而发生变化。因此，笔者采用了92万六面体网格来模拟起钻时井筒内环空流场。

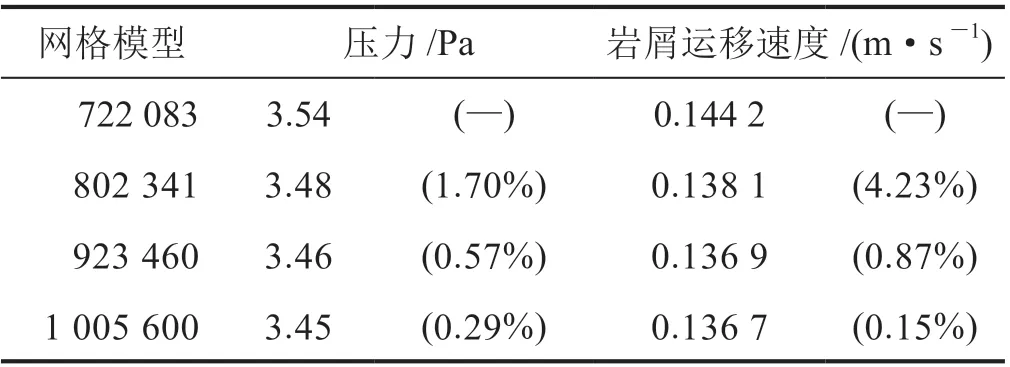
表2 起钻速度0.75 m/s时网格独立性测试结果表

网格划分如图1所示，整个井筒环空流域及钻杆接头附近网格均采用六面体结构网格划分，接头部分由于钻杆形状发生突变，所以在网格划分的时候进行了加密处理。

2.2 模型验证

为了验证模拟所应用的数学模型可靠性，应用Han等[32]的实验参数开展模拟工作，模拟结果与Han的实验数据作对比分析。

Han的实验中，钻井液为质量浓度0.4%的羧甲基纤维素钠（CMC）溶液，岩屑初始注入体积浓度为4%、井斜角变化范围0～60°。图2显示的是环空岩屑运移平均速度随井斜角的变化规律，可以看出随着井斜角从0°～40°区间环空岩屑运移平均速度增幅较为明显，从40°～60°区间环空岩屑运移平均速度虽然增加但是增加速率趋于平缓。数值模拟结果与Han的实验结果吻合较好，平均误差为3.58%。

3 模拟结果讨论

3.1 起钻速度对岩屑床破坏与重新分布的影响

起钻时钻井液中岩屑的运移行为与钻杆轴向运动速度有关，为了研究钻杆轴向运动速度对环空岩屑分布和运移规律的影响，分别模拟了起钻速度为0.10 m/s、0.25 m/s、0.50 m/s和0.75 m/s时的岩屑重新分布的规律，为了研究方便本文定义钻杆从井底运动至井口的过程为钻杆轴向运动1个完整周期（T）（T=起钻位移/起钻速度）。

以起钻速度0.75 m/s、环空岩屑截面积比7.5%为例，图3显示了钻杆轴向运动1个完整周期（T=1.26 s）内环空岩屑动态变化。

由图3中可以看出，钻杆由井底向井口方向做轴向运动，环空钻井液形成反向流动，破坏了岩屑床的初始形态，岩屑颗粒开始启动运移，首先在钻杆轴向运动的托曳作用下，环空岩屑做与起钻速度相同方向的减速运移，随着钻杆轴向运动周期的变化岩屑逐渐向与钻杆起钻速度相反方向运移，即岩屑向井底方向运动并分层逐渐沉积，在环空低边重新堆积形成岩屑床。

图4显示了在不同起钻速度条件下，钻杆轴向运动周期末尾时刻环空岩屑分布云图。

由图4可看出，①随着钻杆轴向运动速度增大，环空岩屑向钻杆轴向运动的反方向（即Z轴正方向）运移，并且钻杆轴向运动速度越大，岩屑向Z轴正方向运移的距离越远，当轴向运动速度从0.10 m/s增大至0.75 m/s环空低边岩屑床沉积最厚的位置，从3.012 m移动至3.598 m，逐渐靠近井底。②起钻速度为0.10 m/s和0.25 m/s时环空岩屑在钻杆接头处和钻杆底部环空低边都有残留，这表明当起钻速度介于0.10～0.25 m/s时，初始的岩屑床存在两种破坏形式，一是钻杆接头通过轴向运动以机械式的“拖拉”作用将岩屑床向井口方向拖动；二是环空钻井液的反向流动冲蚀了部分岩屑床，使其重新沉降分布。两种作用结果叠加后，井筒低边的岩屑床沿着轴向扩散分布，对提高井眼清洁效率没有作用。然而，起钻速度为0.50 m/s和0.75 m/s时，大部分环空岩屑都分布在钻杆底部的环空低边，只有极少部分岩屑残留在钻杆及钻杆接头下方的环空低边，这表明当起钻速度大于0.25 m/s时，初始的岩屑床破坏形式以钻井液反向流动冲蚀为主，岩屑启动后随钻井液向井底方向运移，堆积形成高度较大的丘状岩屑床，为再次下钻带来了不利影响，甚至增加了卡钻风险。

图5显示的是不同起钻速度条件下，岩屑床最大堆积高度截面云图和岩屑床堆积高度变化规律柱状图。由图可知起钻速度由0.10 m/s增大至0.75 m/s时，岩屑在环空重新分布后，岩屑床最大堆积厚度随起钻速度增大而增大，由0.10 m/s时的0.8 mm增加至0.75 m/s时的6 mm。模拟结果表明钻杆轴向运动速度越大，环空钻井液所形成的反向流动速度越大，并且在局部形成漩涡，初始的岩屑床可以完全被冲蚀破坏，较为均匀地在钻井液里分散并向井底方向运移沉积，当远离钻杆后，沉积形成新的沙丘。

图6显示的是在不同起钻速度条件下钻杆运动相同的位移时，环空岩屑运移速度的变化规律。本文中钻杆沿着Z轴负方向做轴向运动，故岩屑速度小于零是岩屑在钻杆轴向运动时，钻杆本体及钻杆接头的机械拖拽作用下与钻杆做同向运动，岩屑速度大于零是钻杆轴向运动时钻杆后方会形成负压区钻井液迅速回流，在钻井液的托曳作用下，岩屑由原来与钻杆同方向做减速运动到最后与钻杆运动方向相反，即沿着Z轴正方向运动。

从图6-a可以看出，钻杆轴向运动会引起钻井液及岩屑的速度波动，起钻速度为0.10 m/s时，前1/4T岩屑速度小于零（即岩屑与钻杆同方向运动），后3/4T岩屑速度大于零，速度波动的幅值为0.127 3，0.75 m/s时从开始至1/4T岩屑速度小于零，之后行程岩屑速度均大于零，速度波动幅值达1.091 4，与0.10 m/s时波幅差值达0.964 1。图6-b显示的是钻杆在一个完整的起钻周期内的环空压力波动曲线，钻杆轴向运动速度越大，环空产生的压力波动幅度越大，起钻时选择一个合理的起钻速度不仅可以避免岩屑堆积形成过厚的丘状岩屑床，而且还可以降低剧烈的压力波动所引起的井壁坍塌和溢流的风险[33]。

3.2 钻井液表观黏度对岩屑床分布的影响

由于钻井液表观黏度不同会影响岩屑在环空中的沉降、运移和重新分布规律，笔者模拟分析了4种表观黏度钻井液对环空岩屑分布及运移的影响规律，如图7所示。

由图7中可知，随着钻井液黏度的增大，环空岩屑浓度不断降低，底部静止岩屑床层岩屑体积分数随着黏度的增大而减小，中间运动床层、顶部悬浮岩屑床层岩屑体积分数随黏度的增大明显增加，这是由于钻井液黏度增大对岩屑沉降的阻力增大，增加了岩屑沉降的时间，其次，钻井液黏度增大对岩屑的剪切作用增强，使得更多的岩屑处于运动状态。

表3比较了钻杆起钻速度和钻井液黏度对钻杆接头处的1.5 m处位置岩屑浓度的影响规律。

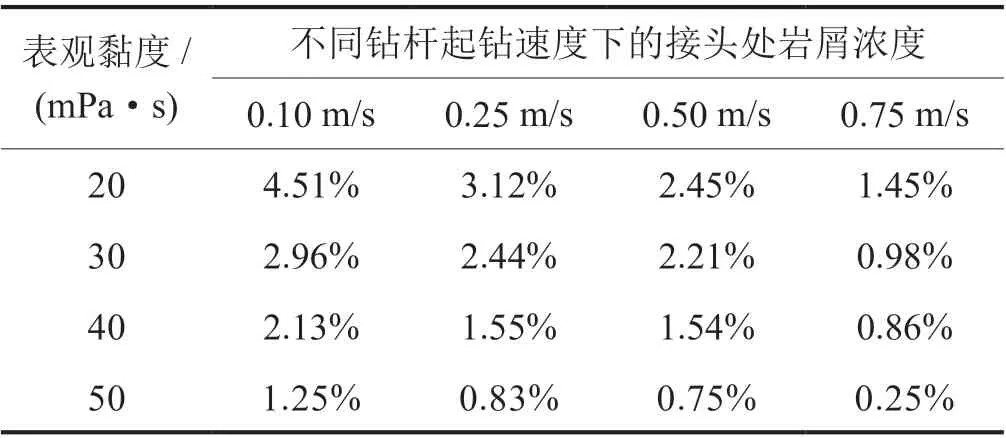
表3 钻井液表观黏度对钻杆接头处岩屑浓度的影响规律表

从表3可以看出，在不同起钻速度条件下，增加钻井液黏度能有效降低钻杆接头处的岩屑浓度，较低起钻速度时钻井液黏度对岩屑浓度的影响更加明显，而在较高起钻速度时钻井液黏度对岩屑浓度的影响程度并不显著。因此，当井眼内钻井液黏度较低时，起钻速度范围可以适当放宽。当井眼内钻井液黏度较高时，应采用较低的起钻速度，有助于控制岩屑重新堆积的砂丘高度，同时高黏度的钻井液可以保障钻杆接头附近不会残留过多岩屑，降低钻杆接头处卡钻风险，减小钻具摩阻力，改善托压问题。

图8比较了在钻杆起钻速度为0.25 m/s的模拟条件下，沿井眼轴向不同位置岩屑体积分数的变化规律，可以看出钻井液黏度小于30 mPa·s时环空岩屑浓度沿轴向呈前高后低的趋势，等于30 mPa·s时钻杆前后环空岩屑浓度接近动态平衡，前后浓度差相对较小，大于30 mPa·s时环空岩屑浓度前低后高，这表明随着钻井液黏度的增大，钻杆和环空间隙之间由于钻井液的黏附作用所产生的抽吸压力增大，并且逐渐取代了钻杆轴向运动时对岩屑的机械拖拉作用，在抽吸压力作用下，钻井液反向流动的冲蚀作用使得环空岩屑不断向井底移动。

4 结论

采用欧拉—欧拉两相流体模型和Realizablek-ε湍流模型，并结合动网格技术给钻杆施加一个轴向运动的速度来模拟起钻时钻杆轴向运动对水平井段岩屑床分布的影响规律。经过实验数据与仿真结果的对比，验证了模型的有效性并得出了以下结论：

1）基于CFD模拟结果可得，当起钻速度处在0.10～0.25 m/s的范围内时，钻杆接头的携屑作用尤为明显，但是钻杆接头的携屑作用只是将原始岩屑床破坏，使岩屑重新沿轴向扩散分布，并没有净化井眼的作用。

2）起钻速度超出0.25 m/s时，会引起井筒中产生激烈的压力波动，使得井筒中岩屑重新分布堆积，形成比初始岩屑床更厚的岩屑床，当速度过大时激烈的压力波动有可能会导致井壁坍塌和溢流。

3）相同起钻速度下，增大钻井液黏度可以使更多的岩屑处于悬浮状态，增加了岩屑沉降的时间，以30 mPa·s为分水岭，环空岩屑分别沿轴向呈前高后低和前低后高的形式分布。

4）井眼内钻井液黏度低（µa<30 mPa·s）时，搭配起钻速度范围可以适当放宽至0.25～0.75 m/s，可以有效控制岩屑床厚度，降低卡钻风险，而高黏度钻井液（µa>30 mPa·s）则对起钻速度要求苛刻，应严格控制在0.10～0.25 m/s。