技术创新与区域经济发展的动态关系研究

巫媛莹 韩芳 刘璇斐

摘 要：经济增长的相关研究一直是经济学领域中最活跃的研究课题之一，经济领域的核心竞争就是技术创新能力的竞争。经济体依靠技术创新能力的增强，不仅能推动经济的增长，更能推动经济的优质增长。通过云南省时间序列数据建立实证模型，通过Granger因果关系检验确定技术创新和区域经济增长之间的因果关系，并利用ECM模型确定技术创新和区域经济增长之间的均衡关系。

关键词：技术创新;区域经济增长;Granger因果关系检验;ECM模型

中图分类号：F224        文献标志码：A      文章编号：1673-291X（2021）16-0050-04

引言

当今世界，科学技术迅猛发展，“技术创新”一词大量充斥于各种媒体，人们越来越真切地认识到技术创新对经济发展所起到的推动作用。对于区域经济发展来讲，技术创新也成为影响其最重要的动力和关键因素之一，发挥着基础性和本质性的作用，深刻地改变着区域经济格局。20世纪90年代以来，经济增长的相关研究一直是经济学领域中最活跃的研究课题之一。相关的经济增长理论认为知识积累、科技进步和高素质的人力资本能够创造规模收益递增效应，从而实现经济的可持续增长。技术创新在当今发达资本主义国家的经济增长中起着越来越重要的作用，并且成为经济增长引擎。今后经济领域的竞争，核心就是技术创新能力的竞争。依靠技术创新能力的增強，不仅能推动经济的增长，更能推动经济的优质增长。本文分析技术创新对于区域经济增长的影响，通过Granger因果关系检验确定序列之间的关系，并利用ECM模型确定序列间的均衡关系。本文的研究结果将丰富技术创新和经济增长的相关研究。

一、文献综述

许多学者已经对分析技术创新对经济增长的贡献方面进行深入而细致的探索研究。用定量分析方法研究技术创新对经济增长的贡献最早开始于20世纪初期。1928年，美国著名数学家柯布（C.W.Cobb）与经济学家道格拉斯（P.H.Douglas）提出经济学中著名的柯布—道格拉斯生产函数（CD函数），这一研究对描述定量的投入及产出之间联系的方法和模型作出十分重大的贡献[1]。柯布与道格拉斯分析了全美制造业从1899—1922年间的历史资料后得出，在生产的投入因素之中，只有资本和劳动是决定性要素，其他要素对产出的影响可以忽略不计[2]。

1942年，荷兰杰出经济学家丁伯格（J.Tingbergen）[3]完成一篇德语文章，文章中作者在资本与劳动投入函数中引入了时间趋势来表示“效率”的水平。从此，CD生产函数中便有了技术这一影响因子[4]。

1957年，美国麻省理工学院研究所的索洛（Solow）首创了索洛增长核算模型[5]，定量的分离出资本、劳动以及技术投入对经济增长的贡献。在索洛模型中所有无法用具体因素解释的增长率被认定为技术进步的贡献。索洛增长核算法在严格意义上来说必须同时满足下列条件：仅有劳动与资本这两个生产要素，并且可以相互替换，还能够以可变比例进行组合;经济系统处在完全竞争状态下，生产要素劳动与资本的边际产出存在递减;劳动与资本在任意时间都得到了充分的利用;技术进步是希克斯（Hicks）中性的。除此之外，索洛模型在实际应用的过程中一般还须要假设规模报酬是不变的。索洛增长核算模型对技术进步的贡献率进行了大概估计，但这一估计还是过于笼统，对技术进步的贡献作用估计过高。该模型所分析的技术进步不但包括了新工艺、新技术以及新产品的使用等通常意义上的技术进步，还涵盖了除劳动与资本投入之外的所有投入因素影响，例如劳动者素养的提升、组织者决策能力的提升以及规模效益等因素，所以索洛模型中的技术进步只是一种广义上的技术进步。

1974年，丹尼森（dwarf F.Denison）[6～8]首先使用增长因素分析法，把经济增长的影响因素划分成总投入要素以及投入要素生产率两类，尤其对投入要素中的劳动投入做了更为详细的划分。作者把劳动投入按照工时、就业、教育程度、性别和年龄进行拆分，资本投入按照住宅工地与住宅建筑、非住宅土地及存货、非住宅建筑及设备划分，最终计算得出各种因素对经济增长的贡献值，使得索洛“余值”大幅度缩小。丹尼森在分析美国国民收入的统计数据时，通过对投入要素的细致划分进而对细分后影响因素的增长率进行了加权和加总的处理，估算出各种投入要素对经济增长的贡献值。研究结果显示，知识的积累发展占技术进步对经济增长总贡献作用的约2/3。丹尼森增长因素分析法因为把影响经济增长的要素划分的十分细致，所以分析技术创新（即知识积累发展）增长对经济发展的贡献就更加准确客观。遗憾的是，许多因素资深的界定十分困难，导致这种方法的推广应用受到了很大的限制。

美国著名经济学家西蒙史密斯库兹涅茨（Simon Smith Kuznets）[2]是最早从数量与结构两方面对经济增长进行分析研究的经济学者之一。他所编写的一系列关于经济增长影响因素分析的著作中提出：影响经济增长的要素，主要包括知识储备的增加、劳动生产效率的提高以及结构方面的改变。首先是知识储备的增涨，作者认定随着社会的逐渐进步与发展，人类社会的社会知识与技术知识的储备会迅速地增加，当这些知识储备被生产者合理利用时，它就将成为经济总量增长和经济结构转变的基础。但知识并不等于生产力，需要在某些特定中介因素作用下才能够转化为生产力。其次劳动生产效率的提高是以高增长率人均产值为标志的现代经济的增长诱因。最后是结构变化，作者提出在经济相对发达的资本主义国家里，经济结构转化十分迅速，所以结构因素对经济增长的贡献相对比较显著，而在不发达国家中，结构转化进程缓慢，导致结构因素对经济増涨的影响相对较小。

乔根森等（Dale W.Jorgenson）[9～10]在丹尼森研究的基础上，进一步将劳动投入与资本投入的增长拆分成质量增长与数量增张，将资本增进型与劳动增进型两种技术进步自索洛余值中分离出去。乔根森在一系列研究中运用超越对数生产函数模型，对数据进行统计分析，其方法的基础核心是依据投入质量及价格变化对投入数据进一步修改。

20世纪末，罗默[11]、卢卡斯[12]等经济学家提出了新经济增长理论，把技术创新内生化，分析了人力资源与知识外溢等问题，相对之前的经济理论有了很大的突破。但是目前经济学界还没有形成比较权威、统一的，基于新经济增长理论的技术创新对经济增长贡献度的分析方法与模型。

19世纪后期，我国经济的快速发展引起了国内外众多学者关注，我国技术创新对区域经济增长的贡献问题也随之成为学者研究探讨的重点。因为方法及数据的局限，先期研究一般都使用了索洛增长核算方法，研究方向也主要集中于全国范围的技术创新对经济增长的贡献方面，其中沈坤荣（1999）[13]、吉川洋（2001）[14]及Lin（2002）[15]等人都取得了比较有代表性的研究成果，可惜这些研究受到各种局限性的影响不曾在技术创新对区域经济增长贡献的方面进行合理的分析。此后，罗佳明等（2004）对技术创新与经济增长之间的关联性进行了研究，研究结果表明两者之间存在因果关系[16]。翟群臻（2005）使用内生经济增长理论的研究方法，运用线性回归模型研究R&D投入、GDP以及R&D投入与GDP比值三者之间的关系，另辟蹊径的估算了基础创新对区域经济增长的贡献[17]。

此后，更多的研究人员将目光投向技术创新对经济增长影响的区域对比。李红松等（2003）使用CD生产函数分别对中国西部、中部及东部地区的技术创新对该区域经济增长的贡献率进行了估算并进行了横向比较，研究結果表明中部及西部地区技术创新对该区域经济增长的贡献明显低于东部地区[18]。丰明等（2006）对丹东市及其周围地区的技术创新和经济增长之间的关系进行了实证分析与比较[19]。近几年来，随着技术手段上所取得的新突破，基于面板数据的前沿技术分析方法成为对国内技术创新对区域经济增长贡献分析演技的先进手段，随机前沿分析法（SFA）逐渐被更加广泛地应用在这一研究领域[20]。

先前关于技术创新对区域经济增长的相关研究，都仅局限于探寻两者之间的相关关系，而缺乏对于技术创新和区域经济增长之间的因果关系和动态平衡关系的研究。本文收集云南省技术创新和经济增长的时间序列数据建立实证模型，探究两者之间的因果关系和动态平衡关系，以此完善先前研究关于技术创新和区域经济增长的相关研究。

二、研究方法和实证分析

（一）研究方法

本文采用平稳性的单位根验证、ADF检验原理、协整检验、Granger因果关系检验和误差修正模型ECM为理论研究方法。为了确定技术创新与经济发展的动态均衡关系，需要选择相应的指标进行计量分析。根据科学性和数据可获取性的原则，选择云南省科学研究与试验发展（R&D）资本存量、科学研究与试验发展（R&D）人员作为技术创新的指标，以国内生产总值（GDP）作为经济发展的指标。

（二）指标时间序列的平稳性检验

为避免时间序列数据的“虚假回归”现象，进行回归时要求所用的时间序列是平稳的。因此，需要对技术创新的指标R&D资本存量（K）、R&D人员（L）和经济发展指标GDP的时间序列进行平稳性检验。为了使时间序列变得更平稳，取各指标的对数，分别记为LNK、LNL和LNGDP。

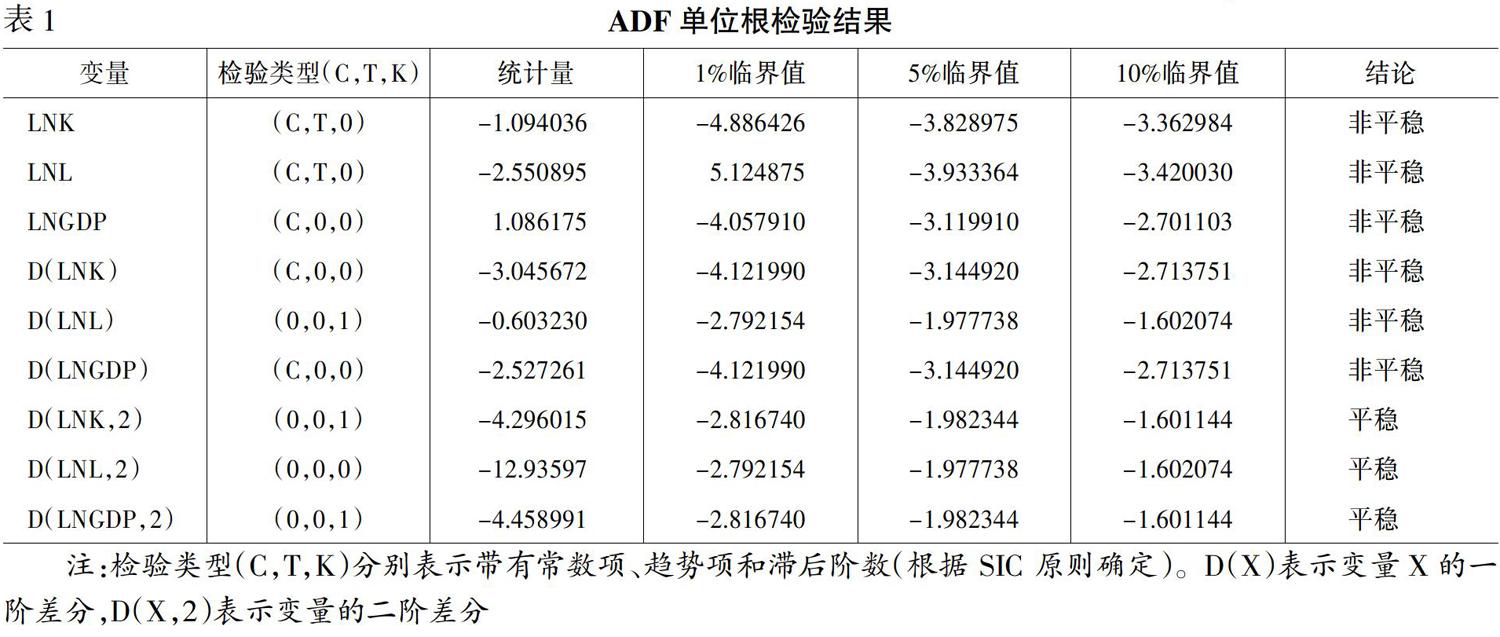
首先对LNK、LNL和LNGDP的时间序列数据进行单位根检验。由图1可知，LNK、LNL和LNGDP的均值都大于0，且LNK、LNL随着时间变化具有一定的趋势，所以进行单位根检验的时候，选择常数和线性趋势。而LNGDP比较平稳，进行单位根检验的时候不考虑线性趋势。滞后阶数采用SIC准则确定。ADF单位根检验的结果如表1所示，根据检验数据，R&D资本存量（K）、R&D人员（L）和经济发展的指标GDP对数的时间序列均不平稳。

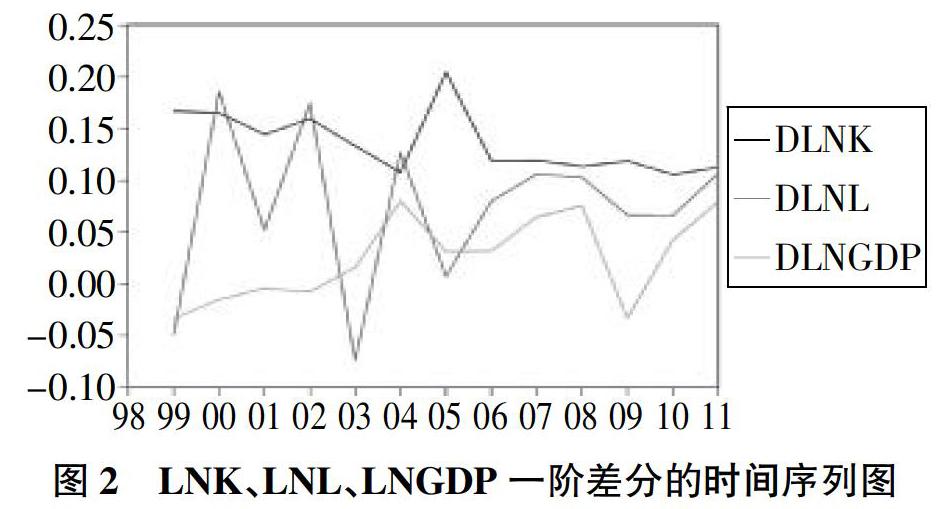
因此，需要继续对其一阶差分后的时间序列进行平稳性检验。LNK、LNL和LNGDP一阶差分的时间序列图如图2所示。由图可知，3个变量的线性趋势均不

明显，所以在检验时均不需要考虑线性趋势。并且除LNL大致围绕0上下波动外，其他2个变量的均值均大于0，所以在检验时除LNL外需要考虑常数项。滞后阶数采用SIC准则确定。进行ADF单位根检验的结果如表1所示，根据检验数据，R&D资本存量（K）、R&D人员（L）和经济发展的指标GDP对数一阶差分的时间序列均不平稳。

继续对变量对数二阶差分后的时间序列进行平稳性检验。LNK、LNL和LNGDP二阶差分的时间序列图如图3所示。由图3可知，3个变量均大致围绕0上下波

动，并且线性趋势均不明显，所以在检验时均不需要考虑常数项和线性趋势。滞后阶数采用SIC准则确定。进行ADF单位根检验的结果如表1所示，根据检验数据，R&D资本存量（K）、R&D人员（L）和经济发展的指标GDP对数二阶差分的时间序列在1%的显著水平下拒绝了存在单位根的原假设，因此，LNK、LNL和LNGDP为二阶单整序列，即LNK、LNL和LNGDP为差分平稳的时间序列，故可以进行协整检验和Granger因果关系检验。

（三）技术创新与经济发展的协整检验

由此回归方程可知，GDP与R&D资本存量、R&D人员之间呈现出正相关关系。根据该回归方程，可得到残差项为：

对残差项？着t进行单位根检验。根据残差项？着t的时间序列图可知残差围绕0上下波动，且不具有明显的时间趋势如图4所示，因此在进行检验时不考虑常数和线性趋势。滞后阶数采用SIC准则确定。ADF单位根检验的结果如表2所示。根据表2中的检验结果可知，残差序列在1%的显著水平下拒绝了存在单位根的原假设，因此残差序列是平稳的，说明GDP与R&D资本存量、R&D人员之间存在协整关系，即三者之间存在长期的稳定关系。根据式（1）可知，从长期来看，R&D资本存量每增加1%，GDP将增加0.02%，R&D活动人员全时当量每增加1%，GDP将增加0.34%。

（四）因果关系检验

协整检验表明，技术创新与经济发展之间存在一定关系，但是没有指明它们之间是否存在因果关系以及因果关系的方向。为了进一步分析云南省技术创新与经济发展之间的关系，需要对R&D资本存量、R&D人员和GDP的对数进行Granger因果关系检验。检验结果如表3所示。

根据表2和表3中的检验结果可以看出，当滞后期为1时，存在LNK、LNL与 LNGDP单向的因果关系，即R&D资本存量、R&D活动人员全时当量的增加能够促进经济发展，而经济发展不能促进R&D资本存量和R&D活动人员全时当量的增加。

（五）误差修正模型

根据协整检验和Granger因果关系检验的结果，可以确定云南省技术创新与经济发展之间存在长期协整关系，且存在R&D资本存量和R&D活动人员全时当量到经济发展的单向因果关系。下面建立LNK、LNL构成LNGDP关系的误差修正模型，并对该模型进行分析。

首先根据式（2）导出误差修正序列：

ecmt=LNGDPt-4.1832-0.0213LNKt-0.3462LNLt（3）

然后建立误差修正模型：

通过最小二乘法（OLS）估计误差修正模型：

整理可得：

误差修正模型中的差分项反映了短期波动的影响，误差项则反映了长期均衡对短期波动的影响。根据式（6）可知，经济发展的波动由短期波动和长期均衡两部分组成。短期波动，即R&D资本存量和R&D活动人员全时当量差分项。长期均衡即误差修正项，误差修正系数为-0.3223，符合反向修正机制，当经济发展短期偏离均衡状态时，误差修正项促使经济发展向长期均衡状态收敛。

三、研究结果和启示

本文介绍了检验技术创新与经济发展动态均衡关系的模型，包括单位根检验、协整检验、Granger因果关系检验和误差修正模型。然后根据科学性和可获取性原则，选择了R&D资本存量、R&D活动人员全时当量作为技术创新的指标，选择国内生产总值（GDP）作为经济发展的指标，并核算了指标的数值。

参考文献：

[1]  Charles W.Cobb，Paul H.Douglas.A Theory of Production[J].American Economic Review，1928，（1）：139-165.

[2]  库兹涅茨.现代经济増涨：发现与反映[G]//现代国外经济学论文选：第2期.北京：商务印书馆，1981.

[3]  Tingbergen.Zur Theorie der Langfristigen Wirtschaftsentwicklung[J].Weltwirtschaftliches Archiv.Band，1942，（1）：511-549.

[4]  Dale W.Jorgenson，Zvi Grileches.The Explanation of Productivity Change[J].Review of Economics Study，1967，（3）：249-283.

[5]  Robert M.Solow.Technical Change and the Aggregate Production Function[J].The Review of Economic and Statistics，1957，（3）：312-320.

[6]  Edwarf F.Denison.Accounting for United States Economic Growth：1929—1969[M].Washington：The Brooking Institution，1974.

[7]  Edwarf F.Denison.Trends in American Economic Growth，1929—1982[R].Washington：The Brooking Institution，1985.

[8]  Denison Edward F.Why Growth Rates Doffer[R].Washington：Brookings Institution，1967.

[9]  Dale W.Jorgenson.U.S.and Japanese Economic Growth，1952—1974：An International Caparison[J].Economic Journal，1978，（12）：707-726.

[10]  Dale W.Jorgenson，M.Fraumeni Barbara.Relative Prices and Technical Change[M].Cambridge：MI Press，1981.

[11]  Romer Paul M.Increasing Returns and Long-Run Growth[J].Journal of Political Economy，1986，（94）：1001-1037.

[12]  Lucas Robert E.，Jr.On the Mechanics of Economic Development[J].Journal of Monetary Economics，1988，（22）：3-42.

[13]  沈坤榮.1978—1997年中国经济增长因素实证分析[J].经济科学，1999，（4）：14-24.

[14]  吉川洋.技术进步与经济增长[J].中国工业经济，2001，（3）：62-66.

[15]  Lin A.A Counting for Economic Growth in Taiwan and Mainland China：A Camparative Analysis[J].Journal of Camparative Economics，2002，（30）：507-530.

[16]  罗佳明，江蕾，范柏乃.中国经济增长与科技投入关系的实证研究[J].科研管理，2004，（9）：104-109.

[17]  瞿群臻.论科技进步、经济增长与就业[J].运筹与管理，2005，（10）：126-133.

[18]  李红松，田益祥.技术进步影响我国经济增长的地区差异比较[J].统计与决策，2003，（8）：38-39.

[19]  丰明，郑杰.科技进步对丹东市经济增长贡献的分析[J].辽东学院学报，2006，（3）：116-119.

[20]  傅晓霞，吴科学.技术效率、资本深化与地区差异[J].经济研究，2006，（10）：52-61.

作者简介：巫媛莹（1989-），女，广东英德人，财务部运营管理科副科长，助理会计师，硕士研究生，从事经济分析、医院运营研究;韩芳（1980-），女，山东济南人，会计师，硕士研究生，从事财务分析、医院资产管理研究;刘璇斐（1985-），女，四川绵阳人，财务部资产管理科副科长（主持工作），会计师，硕士研究生，从事财务及资产管理研究。