艾里光束调控与三维显微成像应用
王 健, 郭宗林
(哈尔滨工业大学 物理学院,黑龙江 哈尔滨150001)
1 引 言
艾里函数是亥姆霍兹方程的精确解析解,据此通过频域调控方法制备的艾里光束具有无衍射、自修复和自加速的特殊性质[1-2],其无衍射特性可使其在传播几个瑞利长度内保持波前稳定。自修复特性可使光束在透过强散射介质和波前畸变后快速恢复波前。自加速特性导致光束在传播过程中表现出横向自弯曲。这些特性使其在光操控[3]、微加工[4]、非线性光学[5]、光学显微成像[6]、湍流大气研究[7]等领域受到关注。
2007年,Siviloglou等人[8]首次提出了基于高斯光束的频域调控方法,在实验中产生了艾里光束,并研究了横向自加速特性。2008年,艾里光束的自修复特性引起关注,Broky理论分析了其物理机制,并通过实验进行了验证[9]。此后,艾里光束的独特传播特性及其显微成像的潜在应用获得深入研究。2014年,艾里光束被制作成光片,用于光片显微镜的激发光场,提高了传统光片显微镜的成像分辨率[10]。同年,Jia等人[11]在随机发射显微镜(STORM)中利用艾里光束调制点扩散函数,提高了三维定位精度,但其自加速特性导致的横向自弯曲传播性能及其应用潜力并未被充分研究。
本文研究一种利用液晶空间光调制器调控艾里光束的自加速特性,并基于光束的横向自弯曲传播调控实现的艾里光束三维重建显微镜。该显微镜具有无扫描高分辨三维成像能力。介绍其工作原理、设计的方法以及实验结果,为红外、太赫兹等其他波段三维成像系统设计提供参考。
2 工作原理与实现方法
2.1 艾里光束的产生与传播特性调控

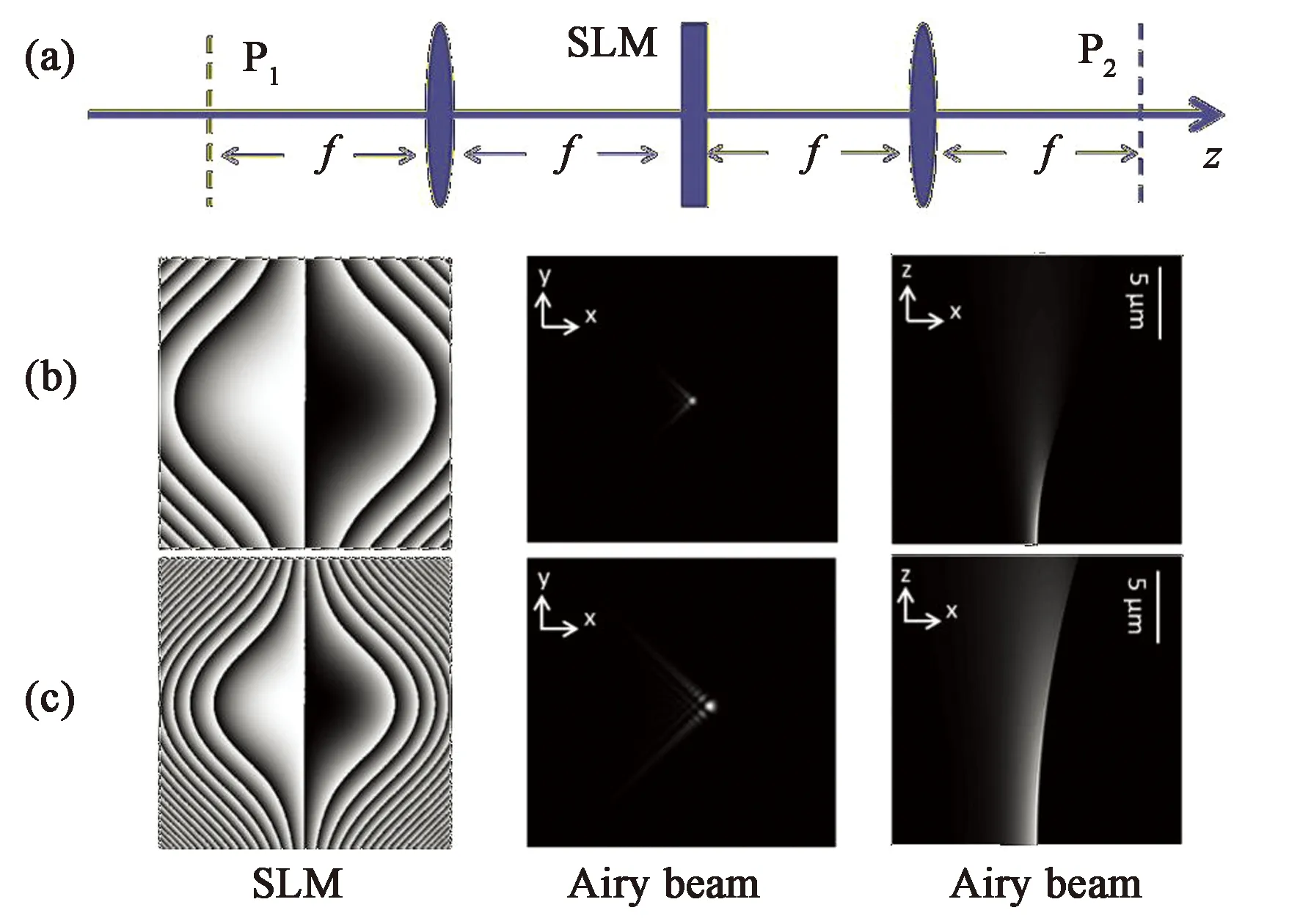
图1 艾里光束的产生光路(a)与不同调制参数的艾里光束(b)、(c)。Fig.1 Set-up for generation of Airy beam (a) and Airy beam with various modulation parameters (b),(c).
调控艾里光束的点扩散函数(PSF)是实现高质量成像的重要手段。为了提高成像的分辨率和对比度,除增大调制图案的参数α,减小艾里光束主瓣尺寸,还需要削弱艾里光束点扩散函数(Poent Spread Functron,PSF)旁瓣(见图1(b),(c)中图尾部)对成像的影响。根据艾里光束PSF的分布特性,本文通过在空间光调制器(Spatial Light Modulator,SLM)平面施加带通滤波器实现PSF旁瓣的压缩。

图2 压缩艾里光束PSF旁瓣的调制图案(a)和实验结果(b)Fig.2 Modulation mask to generate side-lobe-suppressed PSF of Airy beam (a) and experiment results (b)
采取如图2(a)所示的调制图案实现艾里光束PSF旁瓣的压缩。图中,基于图1(b)、(c)的调制图案,在y方向进行了带通截止,截止波矢满足|ky|=kyc,由于|ky|>kyc的部分主要影响艾里光斑的旁瓣分布,合理选择kyc即可调控艾里光束旁瓣的所占比例。此外,我们在调制图案上叠加了闪耀光栅,从而实现+1级调制图像的分离与测量。图中的黄色圆环是高斯光场频谱范围,调制图案中心与高斯光频谱中心重合。图2(b)是在优化kyc后,实验观测的截止前后的艾里光束PSF图像。
2.2 基于艾里光束自弯曲特性调控的三维重建成像设计
根据艾里光束的传播理论,艾里光束在传播过程中具有自弯曲特性,弯曲方向与调制图案的设置有关,且艾里光主瓣的横向平移距离Δl′与轴向传播距离z满足如下关系
(1)
式中,A是自弯曲系数,M是系统的放大倍数,R′代表艾里光斑主瓣直径。因此,对于三维分布的物空间点阵,如图3(a)中的B1、B2、B3,当被调制为艾里光束传播后将在探测面形成投影分布。其中,B1和B2点由于分布在不同的z平面上,其横向平移距离由式(1)确定。B2和B3点处于同一z2平面,因此在探测面的位置关系与z2平面相同。基于上述传播特点可知,经过艾里光束的弯曲传播投影,其等效于人眼以某个侧向角度观察物空间点阵,如图3(b)所示。

图3 基于艾里光束自弯曲传播的三维重建成像原理(a)、(b)与光路图(c),其中OL是物镜,DM是二向色镜,TL是筒镜,FL是傅里叶变换透镜。Fig.3 3D reconstruction imaging principle (a), (b) and set-up (c) based on the self-bending propagation of Airy beam. OL is objective lens, DM is dichroic mirror, TL is tube lens, FL is Fourier lens.
根据以上分析,我们提出,通过改变调制图案,使艾里光束的弯曲方向旋转一周,可以获得物空间点阵不同方向的投影图像,利用Tomography方法对各投影图像进行分析与融合,能够重建物场的三维信息。据此,我们设计并实现了艾里光束三维重建显微镜,其光路如图3(c)所示。该光路基于倒置荧光显微镜Nikon Eclipse Ti-U平台搭建,采用荧光激发模式,激发光源为473,561,647 nm的多波长激光器。在荧光成像面放置偏振片以匹配SLM(反射式,PLUTO-2-VIS-016, Holoeye)进行光束调制。一个4f系统将具有空间结构信息的样品光场转换为艾里自弯曲传播光场,其空间三维分布被倾斜投影至电荷耦合器件(Charge Coupled Device,CCD)面接收。SLM和CCD (Zyla 4.2, Andor) 经电脑连接,由自编程序控制在改变SLM调制图案时实现CCD的同步接收。旋转空间光调制器的图案,可以在接收面得到不同投影角度的多幅二维图像。而后利用自编重建算法,实现三维样品的信息重构。
2.3 基于成像性能提升的艾里光束PSF优化
由于频域调制产生的艾里光束横截面的强度分布具有非对称性,一方面我们采用如图2所示的方法压缩PSF旁瓣,另一方面,我们也采用了函数去卷积方法进一步压缩PSF。如图4所示,构建了不同方向基于实验测量的去卷积函数。经过各投影方向的去卷积处理,提高成像分辨率。

图4 不同方向的去卷积函数Fig.4 Deconvolution function for various direction
此外,采用在调制图案中叠加菲涅尔衍射相位的手段,将成像焦面向轴向的一个方向平移,从而扩大另一方向的成像景深。该方法使成像深度相对于传统高斯成像深度提高了5倍以上[12]。
2.4 三维重建算法设计
为了准确再现目标三维信息,根据艾里光束三维重建原理,本文基于Tomography基本原理设计了三维重建算法,如图5所示。

图5 艾里光束三维重建算法示意图Fig.5 Schematic diagram of 3D reconstruction algorithm for Airy beam
重建过程大体分为3个步骤,第一个步骤根据拉东变换由CCD面的图像坐标(xc,yc,zc)(图5(a),其中zc=0)获得等效直线斜入射的正向投影坐标(x┴,y┴,z┴)(图5(b)),满足如下变换关系:
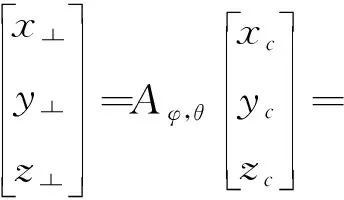
(2)
式中,φ是CCD面相邻两幅投影图的旋转角度,θ是等效倾斜角度,见图3(b)。实验中,若选择等间隔的9幅投影图进行重建,则φ=40°。针对于确定的φ和θ,其平面坐标分布满足如下积分:

(3)
第二个步骤根据光束逆向追迹方法,由最大似然估计算法重建物面三维坐标(xT,yT,zT)。
第三个步骤根据艾里光束传播理论进行坐标矫正,见图5(c)。假定与样品坐标(x,y,z)满足物象关系的艾里光束空间坐标为(x′,y′,z′),则艾里光束横向平移距离Δl′与传播距离z′满足式(1),且(x,y)=(x′,y′)/M,z=z′/M2。因此得到准确的样品坐标(x,y,z)与重建物面坐标(xT,yT,zT)的关系为:
(4)
(5)
(6)
3 实验与结果
3.1 三维重建的分辨率研究
利用艾里光束三维成像显微镜,我们开展了纳米粒子的三维重建实验,采用40×/0.75 NA的物镜测量了显微镜的成像分辨率。实验中使用了平均直径为200 nm的荧光纳米粒子,采用647 nm波段的光源激发,荧光发射中心波段为680 nm,图6是单粒子经过Tomography算法重建后的图像。我们测量了粒子的三维强度分布,通过高斯函数拟合得到了X,Y,Z三个维度的半高全宽,经分析,该显微系统的X方向分辨率约为0.5 μm,Y方向分辨率约为0.6 μm,Z方向分辨率约为1.5 μm。根据实验参数计算,X方向的分辨率接近衍射极限(~0.45 μm)。Y方向的分辨率高于X方向,是由于闪耀光栅在Y方向分光的光斑拉伸导致。Z方向的分辨率超越衍射极限(~2.5 μm)。
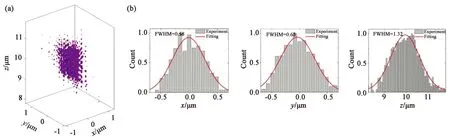
图6 单粒子重建(a)与分辨率测量(b)Fig.6 Reconstruction for single bead (a) and resolution measurement (b)
3.2 投影幅数对成像分辨率的影响
我们研究了一周的不同投影数对三维重建成像分辨率的影响。以等角间隔的方式,分别对一周6幅投影图(旋转角间隔为60°)、9幅投影图(旋转角间隔为40°)、12幅投影图(旋转角间隔为30°)、18幅投影图(旋转角间隔为20°)、36幅投影图(旋转角间隔为10°)进行了单粒子重建,得到图7的实验结果。该结果表明:不同投影幅数对重建图像分辨率的影响很小,可以忽略。根据再现图像质量分析,投影幅数越多,重建图像的点密度越高,因此图像的保真度将更好,但投影图像增多将影响成像速度。综合考虑上述因素,我们选择9幅投影图作为艾里光束三维重建显微成像的最优方案。

图7 不同投影幅数对重建像分辨率的影响Fig.7 Reconstruction resolution vs. projection numbers
3.3 生物细胞成像实验
我们利用艾里光束三维重建显微镜开展小鼠肾细胞10 μm切片的成像实验,见图8。相对于传统的Z扫描成像机制,艾里光束三维重建显微镜具有无扫描、高对比度的成像特点,以1 μm的间隔对肾小管的z向分布进行断层成像,能够清晰分辨小鼠肾管的结构变化,见图8(a)。

图8 小鼠肾细胞的单色成像(a)与双色成像(b)Fig.8 Imaging of single color (a) and two-color (b) for mouse kidney cell
我们也研究了该显微镜的双色重建特性,分别比较了激发光波长561 nm和473 nm在深度z=4 μm处的传统高斯光场成像和艾里光场成像,如图8(b)所示,能够看到两种成像模式符合得很好,但艾里光场成像具有更高的信噪比。此外,根据式(1)分析了波长对重建坐标位置的影响,并进行了坐标校正,图8(b)对两个波长的艾里光场成像进行了融合。由于细胞不同位置的荧光染料标定不同,通过不同波长激发将获得更为丰富的结构信息,为深入理解细胞结构提供了一种有效手段。
4 结 论
以空间光调制器为核心器件,采用频域调制手段产生了艾里自弯曲光束。该光束的传播距离、弯曲方向和弯曲角度可通过频域调制图案调控,具有无衍射、自修复等适用于高分辨显微成像的独特性质。以调控艾里光束产生不同角度的自弯曲投影图像为核心思想,我们设计并实现了艾里光束三维重建显微镜,通过对点扩散函数的优化,实现了高分辨率的三维显微成像,在40×/0.75 NA物镜下实现了横向分辨率约为0.5 μm,轴向分辨率约为1.5 μm。小鼠肾细胞的实验研究证明了艾里光束三维重建显微镜相对于传统Z扫描三维成像具有无需机械扫描、成像深度可达10 μm以上、具有更高信噪比等优势,且适用于多色成像以更精准地解析细胞结构。
据此分析,以9幅投影图像作为最佳重建方案,使用动态刷新率为60 Hz的空间光调制器预计可实现6幅/s的三维重建速率,满足一般的细胞动态观测需求。艾里光束三维重建显微镜的成功实现也证明,基于空间光调制器的光场调控技术应用于光学成像领域,带来了诸多新的研究问题,产生了新奇的研究结果,也将会为红外、太赫兹等其他波段的成像研究带来新的启发。

