基于二次清运的回收车辆路径研究*

李志滔，方雄发，吴雪菲，许家玮，张智聪

（东莞理工学院机械工程学院，广东东莞 523808）

0 引言

随着城镇化的快速发展，一些城市出现了智能垃圾回收机柜，机柜垃圾的清运问题也日益突出，规划车辆行驶路径成为了公司降低经营成本的重要途径之一。在车辆回收垃圾的过程中，若机柜的回收量达到其容量前还没有被清运时，就不能及时为居民提供服务，会降低居民对服务的满意度；若回收车辆到达的时间早于机柜达到标准垃圾量的时间，车辆就得等待或者提前清理垃圾，如果等待时间过长，则不利于公司的运营，如果清理时间过早，则会影响后面的工作安排。当前，大多数公司的清运策略是员工凭借对道路的熟悉度来确定清运路径[1]，而经过科学规划的路径可以减少车辆行驶的总路程，降低经营成本。因此，科学的路径规划是解决清运成本与清理机柜准时性的重要任务。

资源回收的车辆调度是现代化物流系统的重要环节之一，是指调度中心根据不同地方资源的产生量，及时派送车辆对该地方的资源进行回收并回到起点的过程。VRPTW问题的求解方法大体可分为精确算法和启发式算法，许多学者对VRP问题的复杂性进行分析，得出几乎所有类型的VRP问题都是NP－hard问题[2]。贾定芳[3]在硬时间窗的前提下，构建以车辆行驶路径最短为目标的模型，解决配送服务，平衡配送成本和顾客满意度这两个目标解决了生鲜外卖配送路径规划问题[4]；陈婷[5]改进遗传算法对快递的VRPTW模型进行求解；陈梅[6]在计算遗传算法的过程中使用禁忌搜索算法对城市环卫车调度进行优化求解；牛群[7]针对带硬时间窗车辆路径问题，提出了一种改进型烟花算法进行求解，该算法能够利用信息交互进行资源分配；在二次调度问题的研究上，李冲等[8]研究了货物配送中在保证时间窗的前提下，需要同一辆车进行二次或多次配送；杨天杰[9]优化成品油二次物流配送车辆调度问题，减少配送成本。

本文以车辆行驶的总路程为目标进行优化，结合第二次回收车辆调度的特点，在硬时间窗的约束下，建立综合考虑两次清运的混合整数规划模型进行求解。

1 数学模型构建

1.1 问题假设

数学模型构建的问题假设如下。

（1）回收车辆在两机柜间行驶时间与距离具有一定的线性关系，忽略堵车等特殊情况。

（2）每个机柜的回收量与时间具有一定的线性关系，忽略节日、恶劣天气等特殊情况。

（3）两机柜间距离和所需的行驶时间以高德地图推荐的路线为依据。

（4）每辆回收车辆的型号相同、油量充足。

（5）具体清运过程的时间忽略。

1.2 二次清运分析

根据历史数据显示，每个机柜的回收量与时间成强正相关，在数学模型的建立过程中可以认为回收量与时间具有线性关系。当机柜被清运完成一次后，其回收量在本工作日内再次达到最大回收量时，必须安排车辆对该机柜进行第二次清运。第一次回收车辆调度模型是一个带时间窗的VRP模型，其局限性是没有考虑全局的车辆调度情况，以至于在整个工作日内所有车辆的总里程极大可能不是最优的。因此，综合分析第一次和第二次回收车辆调度，才能在整个车辆调度中找到车辆总里程的最小值。

在模型建立的过程中，需要求出第一次实际清运的时间，需二次清运机柜的时间窗是该机柜第一次清运时间窗与第一次实际清运时间之和，第二次清运模型的约束建立与第一次的模型具有相似性。回收车辆调度模型简图如图1所示。

图1 回收车辆调度模型

1.3 问题描述

清运中心C共有K辆回收车辆，每辆车的最大载重为Q kg，其负责的片区共需清运L次，包括第一次和第二次清运。第一次回收车辆必须在机柜达到标准回收量的时刻t1i和最大回收量的时刻t2i之间到达机柜；第二次回收车辆必须在机柜第二次达到标准回收量时刻s1i和最大回收量时刻s1i之间到达。回收车辆统一从清运中心C出发，在达到最大载重Q前返回清运中心卸掉可回收资源。每条清运路径的总回收量应小于或等于回收车辆的最大载重。

1.4 参数与符号定义

（1）符号定义

i(1≤i≤L)为机柜序号（包括第一次和第二次清运时机柜的序号，其中第一次清运的机柜序号在前，紧接是第二次清运的机柜序号，同一机柜的二次清运序号相差L－N）；j(1≤j≤J)为机柜在其回收车辆j所清运的所有机柜中的排序号（需要事先估算J值，J值为每辆车清运的机柜数量的最大值）；k(1≤k≤K)为车辆序号（K值为可能使用车辆的最大数目，需要事先估算K值）；Q为回收车辆的最大载重；J为每辆车清运的机柜的最大数目；K为可能使用车辆的最大数目；N为需要进行第二次清运机柜的数量；ai、bi分别为回收量与时间线性方程的斜率和截距；di1,i2为机柜间距离；gi为从清运中心去到各个机柜的距离；fi为从各个机柜回到清运中心的距离；Ti1,i2为前往下一个机柜需要行走的时间；t1i、t2i分别为机柜垃圾量到达标准回收量和最大容量的时刻；M为一个很大的数（比如100 000）。

（2）定义决策变量

定义决策变量为：

例如，x2,3,5＝1为第2辆车清运的第3个机柜是机柜5。

s1i、s2i分别为二次清运机柜垃圾量到达标准回收量和最大容量的时刻；sk,j为第k辆车到达第j个清运位置（机柜）的时刻；yk,i为车辆k清运回收柜的数量。

1.5 模型建立

（1）目标函数

目标函数如下：

从清运中心出发，回收车辆完成收集后再回到清运中心的总里程最短。

（2）约束条件

约束条件如下：

式（1）～（2）为所有机柜都要被清运。

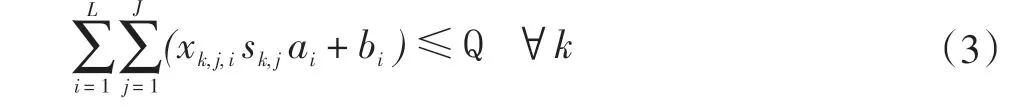
式（3）为清运路程中所有机柜回收量之和不超过回收车辆的最大载重量。

式（4）为每辆车每个清运排序号最多只能清运一个机柜。

式（5）保证不能出现车辆最后的一个机柜还安排了一个机柜的情况。式（6）保证了车辆k清运的第j个、第j＋1个机柜分别为i1、i2。

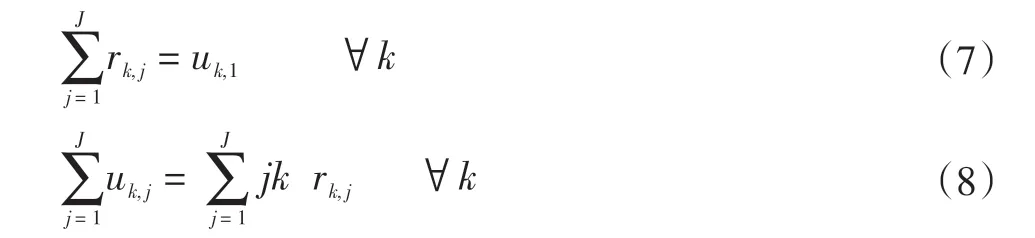
式（7）～（8）判断第k辆车的第j个机柜是否是终点。

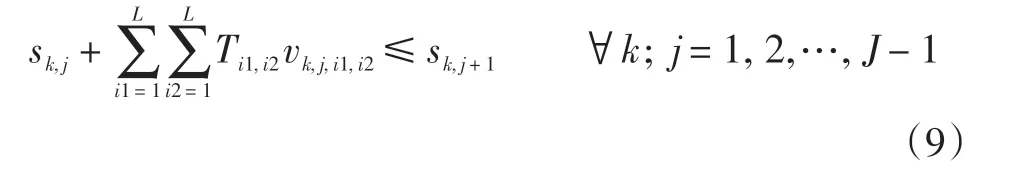
式（9）为第k辆车到达第j机柜的时间不大于第k辆车到达第j＋1机柜的时间。

式（10）保证车辆k清运的第j个、第j＋1个机柜不是i1、i2（i1＝i2）。

式（11）为第一次清运的时间窗约束：车辆到达第j个、第j＋1个机柜时，必须在机柜回收量到达标准回收量的时刻与到达最大容量的时刻之间到达。

式（12）～（13）分别为二次清运机柜垃圾量到达标准回收量和最大容量的时刻。

式（14）～（15）为第二次清运的时间窗约束：车辆到达第j个、第j＋1个机柜时，必须在机柜回收量到达标准回收量的时刻与到达最大容量的时刻之间到达。

1.6 非线性约束向线性约束的转化

日常生活中的优化问题普遍是非线性规划问题。非线性规划问题是指目标方程或约束中存在至少的非线性函数的最优化规划问题。大多数约束最优化的方法可通过将有约束问题转化为无约束问题求解。冯迎春[10]介绍了解决约束优化问题的算法主要有可行方向法、L－N法、逐步二次规划法等。

在运筹优化中，通过引入大M法把非线性约束转化为线性约束的方法，是解决非线性问题的常用方法。非线性规划向线性规划转化的模型可以较大地减少求解模型最优解的时间。

数学模型中非线性约束向线性约束的转化如下。

式（3）转化为

式（12）转化为

式（13）转化为

2 实例分析

本文以东莞某环保科技公司为研究对象，选取该公司所负责松山湖片区附近的23个清运机柜进行路线规划，该片区有1个清运中心和7辆可供使用的回收车辆，回收车辆的最大载重为250 kg，在达到最大载重时必须返回清运中心卸掉垃圾，机柜的标准回收量为40 kg，最大容量为50 kg。

2.1 实例数据处理

通过对该公司历史数据的处理，得到23个机柜间的行驶路程、清运中心与机柜间的行驶路程、回收车辆在机柜间的行驶时间、机柜回收量达到40～50 kg的预测时间点和回收量与时间的回归方程的斜率和截距。再根据回归方程计算出需要进行二次清运的机柜，在原数据基础上，对其进行相似的处理。在机柜编号的过程中，需二清运机柜的第一次编号分别为1，2，…，7，紧接的是不需二次清运机柜的编号为8，9，…，23，再接着的是需二清运机柜的第二次编号为24，25，…，30，即编号1～7与编号24～30的7个机柜对应着的是同一个机柜。

2.2 实验结果分析

ILOG OPL软件编程求解结果显示，在硬时间约束下，清运中心只需6辆回收车辆就能完成包括二次清运在内的工作，每辆车分配的任务均匀，而多出的一辆车可以减少一位驾驶员，降低雇佣成本。实验所求出的结果如表1所示，表中括号内外的编号表示同一个机柜。

表1 实验结果分析表

3 结束语

本文研究了硬时间窗约束下回收车辆调度问题，以多车辆的两次清运为研究对象，以行驶路程最短为目标，构建混合整数规划数学模型，实现了对回收车辆的系统性调度。实验运行过程中，非线性约束向线性约束的转化，较大地节省了求解时间。结果表明，松山湖片区的清运路径得到系统化的规划，同时确定了最优回收车辆数量和满足时间约束条件下的最短行驶路径。而对于大规模数据的处理方面，可以继续开展智能算法方面的研究。