一种基于快速RLS的主动控制算法研究*

黎思廷，刘树勇，杨理华

（1.海军工程大学动力工程学院，武汉 430000；2.海军潜艇学院，山东青岛 266000）

0 引言

机械设备的振动与噪声是机械设备的一项重要性能指标。振动噪声控制在各种动力机械设备都有着广泛的应用。其中主动控制有着优良的灵活性，在低频的振动噪声控制上具有较好的效果[1]。

算法的鲁棒性和收敛性研究是主动控制研究的一项重要工作。现在最常用的算法是基于自适应滤波的LMS算法和RLS算法[2]。其中RLS算法因具有较好的收敛速度而受到关注，但其计算复杂度较高。对此，国内外很多学者在RLS算法的优化方面做了大量研究。Cioffi[3]提出了基于FTF的快速算法，该算法可以有效减少算法复杂度，但降低了计算复杂度的同时，也使稳定性变差；Slock[4－5]对该算法进行了改进，通过反馈参数对非稳定量进行修正，增加其稳定性；Boudreau[6]考虑了时延和未知系统的参数，使其加权平方误差达到了最小；陈克安[7]提出了一种IRLS算法，其在时延范围内不进行收敛，可以在这段时间内减轻一定的计算量；宁少武[8]提出了格型联合估计滤波器结构与基于QR分解的最小二乘格型（QRD－LSL）自适应滤波算法相结合的噪声控制方法，可以有效提高收敛速度并减小计算量；宫赤坤[9]利用滤波－U卡尔曼算法来进行控制，有效提高了控制性能；罗顺安[10]利用ADAMS建立齿轮箱虚拟样机模型并利用FXRLS算法进行了联合仿真，取得了较好的效果。基于FTF的快速稳定算法具有最小的计算量，且与经典RLS算法的性能相差不大，是最主流的快速算法之一。

为了进一步减少RLS算法的计算量，本文首先对该算法的计算复杂度进行了优化，然后通过变遗忘因子的方法对该算法进行了分析。通过仿真验证，改进过的算法在对于旋转机械设备产生的周期性振动噪声方面有着较好的控制效果。

1 RLS算法分析

相对于LMS算法而言，RLS算法的收敛速度更快[11]。经典RLS算法的过程如下。

输入向量x(n)，期望向量d(n)，初始权值w(n)，以及参考定义矩阵p(n)，其代价函数为：

令：

式中：λ为遗忘因子（0＜λ＜1）。

更新参考矩阵：

将RLS算法应用到主动控制技术中，如图1所示，即FXRLS算法。研究表明，在收敛速度等方面，FXRLS算法性能优于FXLMS算法，但其算法计算量比较大。当采用长度为L的横向滤波器，FXRLS算法的计算量比FX⁃LMS算法多（3L2＋L）次。

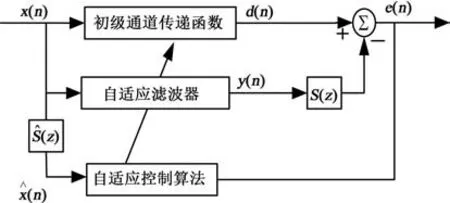
图1 FXRLS算法结构图Fig.1 Structure diagram of FXRLS algorithm

2 快速RLS算法

虽然RLS算法在收敛速度等方面强于LMS算法，但在计算量方面相对较大。为了克服这一缺点，可以采用快速RLS算法来进行改进。快速RLS算法主要为格型算法[12]和FTF（快速横向滤波器）算法[12]。

本文利用前向和后向预测来减少RLS算法的计算量，从而得到FTRLS算法。其原理如图2所示，为增加其稳定性，引入求助变量这一反馈机制，得到SFTRLS算法。

图2 FTRLS算法框图Fig.2 FTRLS algorithm block diagram

快速RLS算法的过程如下。

（1）定义参数

输入向量xN(n)，期望输出d(n)，权向量wN(n)，增益向量kN(n)，性能参数aN(n)、gN(n)，最小二乘和的初始值。

（2）前向预测

先验估计误差：

后验估计误差：

最小二乘和：

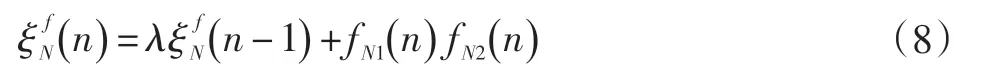
转换因子：

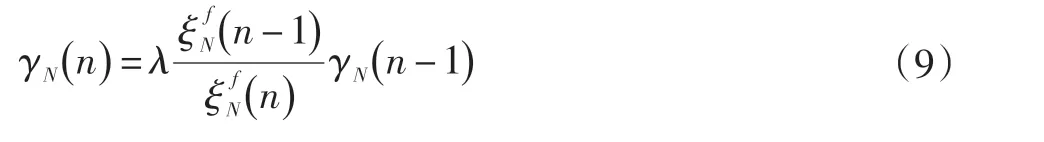
增益向量为：

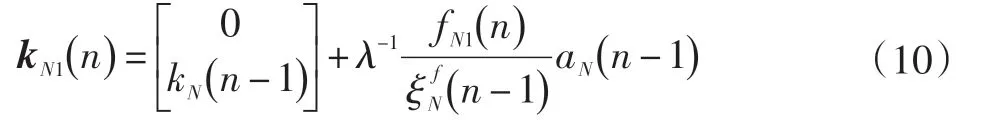
（3）后向预测

先验误差估计：

求助变量：

转换因子：

后验误差估计：

最小二乘和：

增益的计算：

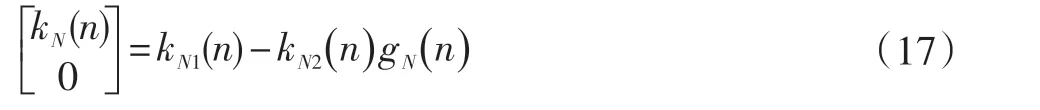
迭代：

（4）联合估计过程

前向预测误差信号：

后向预测误差信号：

权值更新：

其中，求助变量在一定程度上增强了算法的稳定性。

将快速RLS算法与经典RLS算法进行对比仿真。如图3所示，从图中可看出，其收敛性能并没有非常明显的变化。计算复杂度从L2量级下降到了L量级，显著减少了其计算量。

图3 快速RLS算法与经典RLS算法的比较Fig.3 Comparison of fast RLS algorithm and classic RLS algorithm

3 快速RLS算法遗忘因子选取

遗忘因子是RLS算法的一项重要参数，主要用于增加新数据的权重，以增强对非平稳信号的适应性，标志着该算法具有对输入过程特性变化的快速反应能力。如图4所示，当λ较小时，收敛速度较快，但其对噪声信号敏感，稳态误差较大并且算法稳定性相对较弱。为解决收敛速度和稳定性的矛盾，可以引入变遗忘因子。在初始阶段或者系统发生突变时，即误差较大时，λ值相应地变小，以获得较快的收敛速度和跟踪速度；而在系统进入平稳状态后，即误差较小时，λ值相应地增大，以获得较小的稳态误差。

图4 遗忘因子对RLS算法的影响Fig.4 The influence of forgetting factor on RLS algorithm

根据大量的仿真实验结果可得出，快速RLS算法遗忘因子的取值范围为：

在这个范围之内才能保证算法的稳定性，N为滤波器阶数。当取值如其为最优数值特性。

如图5所示，取N为4，当λ＝0.92时，其收敛速度和稳态误差都相对较好。

图5 遗忘因子最优解Fig.5 Forgetting factor optimal solution

4 仿真分析

对改进的算法进行仿真验证。采用正弦信号和白噪声叠加的方式来模拟激励信号，研究振动控制后系统的响应。设置滤波器阶数N＝17，长度L＝2 000，设置采样频率为10 000 Hz。

正弦输入信号为：

白噪声信号为高斯白噪声。

分别采用FXLMS算法和优化后的快速RLS算法进行对比仿真。两种算法在时域下的仿真图形分别如图6～7所示。由图可知，FXLMS算法约在迭代次数为1 400次时实现收敛，而优化后的RLS算法约在迭代次数为300时实现收敛。仿真结果证明，优化后的快速RLS算法有着更好的收敛性能。

图6 FXLMS算法在时域下的仿真图形Fig.6 Simulation graph of FXLMS algorithm in time domain

图7 改进RLS算法在时域下的仿真图形Fig.7 Improved simulation graphics of RLS algorithm in time domain

对图6～7利用FFT进行频域分析，得到两种算法在频域下的仿真图形，如图8～9所示。从图中看出，FXLMS算法在频率为30 Hz时，幅值降低了0.87，即1.21 dB；在频率为60 Hz时，幅值降低了0.42，即7.54 dB；在频率为90 Hz时，幅值降低了0.15，即16.48 dB。优化后的RLS算法，在频率为30 Hz时，幅值降低了0.91，即0.82 dB；在频率为60 Hz时，幅值降低了0.48，即6.38 dB；在频率为90 Hz时，幅值降低了0.18，即14.89 dB。即该算法相对而言性能更加良好，有着更好的控制效果，从而为振动主动控制的实际应用提供了有效参考。

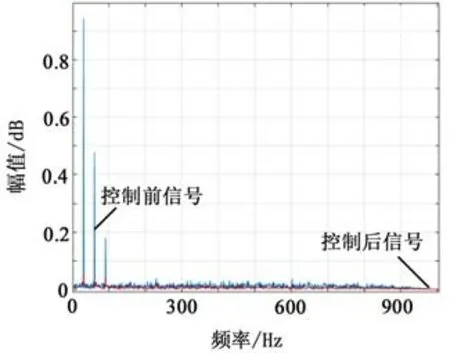
图8 FXLMS算法在频域下的仿真图形Fig.8 Simulation graph of FXLMS algorithm in frequency domain

图9 改进RLS算法在频域下的仿真图形Fig.9 Improved RLS algorithm simulation graphics in the frequency domain

5 结束语

本文针对RLS算法计算量大的缺点，利用横向滤波器对RLS算法进行了改进。通过向前和向后预测推导了FTRLS算法，减少了传统RLS算法的计算量，使运算量从O（L2）级下降到O（L）级，并通过求助变量增强了计算的稳定性。仿真研究表明该方法有较好的控制效果。