混响室内模拟电磁衰落环境的一种普适性方法
茹梦圆,张雪莹,闫丽萍,赵 翔
(四川大学 电子信息学院,四川 成都 610064)
0 引言
混响室是一个电大多模、高Q值的金属腔体,由金属外壳和搅拌装置组成。各种搅拌装置的存在使得混响室的电磁环境不断发生变化从而产生随机变化的电磁环境[1]。由于室壁和搅拌器对电磁波的多次反射使混响室天然具有模拟多径衰落传输环境的特性,所以混响室在模拟实际无线通信信道方面被大量研究[2-5]。常见无线信道中的电磁衰落环境有瑞利分布、莱斯分布、Nakagami分布、对数正态分布和韦伯分布等。经典混响室的电磁环境理想状态是场分量符合瑞利分布,即电场各直角分量的大小(如|Ex|)满足瑞利分布[6-8],所以混响室本身就能模拟瑞利分布场环境。2006年Holloway等人[9]通过在混响室内添加吸波材料和使用不同数量的信号源实现了莱斯分布场环境的模拟。2008年Valenzuela等人在混响室内通过天线阵列实现了各向异性瑞利分布电磁环境的模拟。2013年王皓等人通过混响室模拟了服从瑞利分布的雷达杂波信号。2016年Nguyn等人通过使用多个搅拌器的方式在混响室内实现了用于手机等电子设备测试的瑞利衰落环境。2019年李欢等人[10]进一步研究了发射天线和接收天线正对放置的距离、频率以及损耗物加载量对混响室内电场莱斯K因子的影响。对于混响室内模拟Nakagami分布、对数正态分布和韦伯分布场环境的研究目前尚未见报道。但是目前随着5G通信的发展,在各种电磁环境下对电子设备进行测试的需求日益增多,所以在混响室内实现各种无线信道模型从而代替耗时耗力的实地测试具有非常重要的意义。基于此,在统计学理论的基础上提出了一个筛选算法,通过对采样样本的筛选在混响室中进行了常见电磁衰落环境的模拟,并用拟合优度检验方法进行了验证。
1 常见电磁衰落环境
在电磁波传播过程中,由于传播媒介和传播途径随时间变化而引起接收信号强弱变化的现象称为电磁衰落。电磁衰落环境主要分为小尺度衰落和大尺度衰落[11],常见的衰落模型有瑞利模型、莱斯模型、Nakagami模型、对数正态模型和韦伯模型等。
1.1 瑞利模型
瑞利模型是最常用的小尺度衰落模型之一,通常被用来描述城区街道的衰落环境。瑞利衰落环境的特性是:反射波从各条路径上到达接收端,且各条路径上的信号强弱均衡。根据中心极限定理,电场各分量的实部Er和虚部Ei都服从均值为0,方差为σ2的正态分布,则各分量的幅值服从瑞利分布[12],其概率密度函数为:
(1)
1.2 莱斯模型
当各个方向的反射波信号强弱并不均衡时,比如发送端和接收端之间存在直射分量,接收机处接收到的直射波信号明显占优,那么该环境一般服从莱斯分布,其概率密度函数为:
(2)
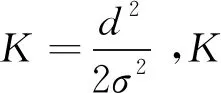
1.3 Nakagami模型
与瑞利和莱斯模型不同的是,Nakagami模型没有具体的物理模型与之对应,而是根据现场测试结果和Gamma分布的概率密度函数进行拟合,拟合效果比瑞利和莱斯信道更接近真实信道,可适用于大部分实际电磁环境[13]。其概率密度函数为:
(3)

1.4 对数正态模型
在电磁波的传播路径上,遇到建筑物、高大的树木等障碍物阻挡时,在阻挡物的背面,会形成电波信号场强较弱的阴影区,这一现象叫阴影效应[14]。大多数情况下,阴影衰落下接收信号的包络近似服从对数正态分布,其包络的概率密度函数为:
(4)
式中,μ和σ是取对数后的均值和标准差。
2010年,Renz等人[15]研究发现对数正态分布刻画了室内障碍物和移动的人体造成的阴影效应特征,能很好地对室内电波传播环境的衰落进行建模。2019年,赵翔等人[16]对四川大学校园内的电磁环境进行了测量,发现3个正交分量及总场幅值的概率密度函数均服从对数正态分布。所以对数正态模型能很好地适用于室内和室外环境。
1.5 韦伯模型
当有大量的无线传输路径时中心极限定理才成立,衰落环境才服从瑞利分布。如果传输路径数量有限,那么瑞利模型就描述的不是很准确[17]。而实验表明,韦伯模型能很好地模拟这种电磁环境[18]。韦伯模型的概率密度函数为:
(5)
式中,Ω是尺度因子;β是形状因子。当β=1时,f(x)服从指数分布,当β=2时,f(x)服从瑞利分布。
和Nakagami模型一样,韦伯模型通过改变形状因子能够灵活地模拟指数分布和瑞利分布。此外,韦伯模型也能很好地用于室内和室外电磁环境的模拟[19-20]。
2 混响室中样本数据的获取和筛选
在实验室中已有的一个矩形机械搅拌混响室内进行了实验[21]。该混响室由一个可伸缩的金属支架支撑,柔性铝箔材料搭建,尺寸为3.3 m×2.0 m×2.3 m。混响室的工作频率在2 GHz以上,对应模式数超过30 000个,完全满足IEC标准[22]。混响室的系统结构如图1所示,实验测试系统如图2所示。
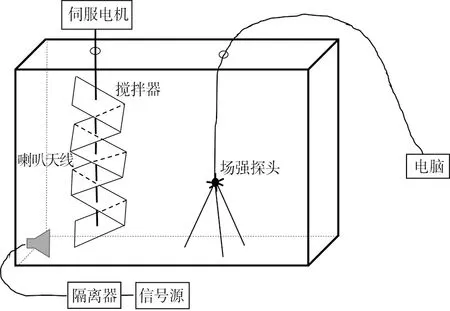
图1 混响室系统结构

图2 试验系统实物
实验设备包括10 MHz~20 GHz的Hittite信号源、隔离器、作为定向发射天线的双脊喇叭天线、FSH13手持式频谱分析仪及配套的各向同性天线、作为接收天线的EP600场强探头、显示场强探头读数的笔记本电脑等。
为了能够得到更多的独立样本点,在混响室中加入了频率搅拌方式。频率搅拌通过线性扫频的方式实现,扫频步长为100 kHz,扫频范围为2.4~2.5 GHz。信号源功率为0 dBm,每个频点停留0.3 s,在此条件下通过场强探头连续采样。在探头0.3 s的采样间隔下,一个扫频周期得到大约1 000个采样数据。采样2次,得到的数据如图3所示。从图中可以看到,2次采样结果几乎完全一致,这说明该混响室能够提供可重复的场环境。

图3 场环境采样结果
为了让样本数据满足特定统计分布(如上述的莱斯、Nakagami、对数正态和韦伯等分布),本文对这些数据进行了筛选,算法流程图如图4所示。

图4 筛选算法流程
主要筛选步骤如下:
① 对得到的样本数据进行统计分析,得到频数直方图;
② 用实际电磁衰落环境的相关模型参数,通过蒙特卡罗模拟生成期望分布的频数分布曲线;
③ 对期望分布的频数分布曲线和样本数据频数直方图进行比较。当直方图某个分组区间内的采样点数量过多,即该分组区间的直方图频数大于期望分布曲线的频数时,该区间需要删除部分采样点。所需删除采样点数量即为两频数之差,按采样时间先后对这些采样点进行删除。
④ 对筛选后的数据继续进行统计分析,将直方图与期望分布曲线进行对比,计算二者之间的误差。不断重复上述过程,当误差不再明显减小时停止筛选。
以电场的x分量为例,样本数据的频数直方图如图5所示,现在通过筛选算法对以下各种参数的无线衰落信道进行仿真模拟。
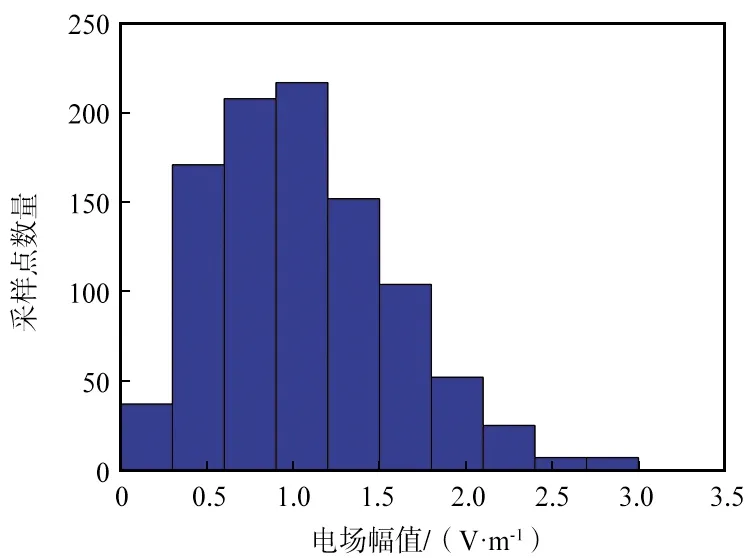
图5 样本数据频数直方图
① 标准差σ=0.83的瑞利分布。
② 直射波信号峰值d=0.74,标准差σ=0.53的莱斯分布(K=0.98)。
③ 尺度因子Ω=1.5,形状因子β=0.5的Nakagami分布。
④ 均值μ=-0.41,标准差σ=0.55的对数正态分布。
⑤ 尺度因子Ω=1,形状因子β=1的韦伯分布。
从得到的瑞利分布(如图6所示)、莱斯分布(如图7所示)、Nakagami分布(如图8所示)、对数正态分布(如图9所示)和韦伯分布(如图10所示)筛选结果来看,筛选出数据的分布情况基本与期望分布一致,说明筛选算法有效地实现了对各种衰落模型的模拟。
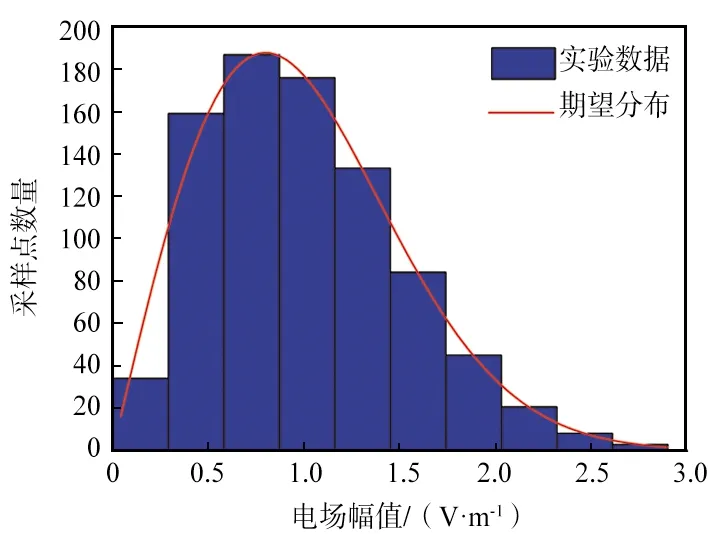
图6 筛选算法对瑞利分布的模拟结果

图7 筛选算法对莱斯分布的模拟结果
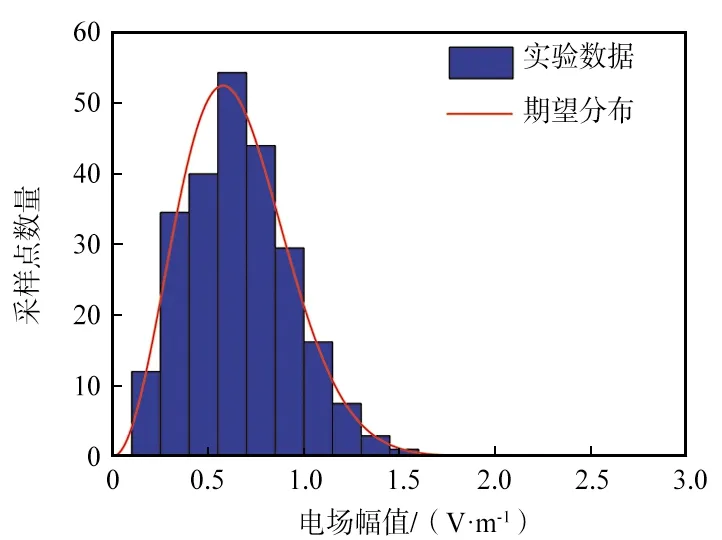
图8 筛选算法对Nakagami分布的模拟结果
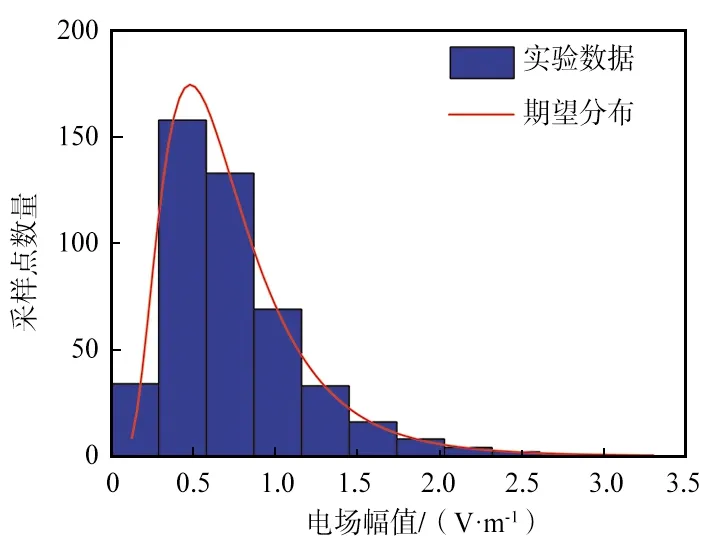
图9 筛选算法对对数正态分布的模拟结果
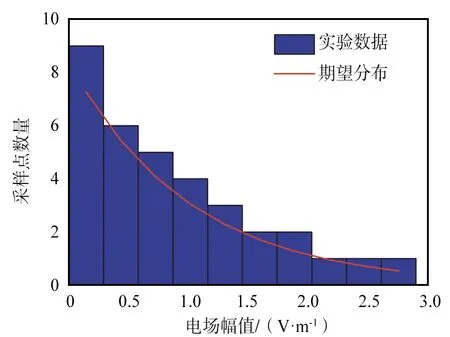
图10 筛选算法对韦伯分布的模拟结果
3 混响室模拟多种衰落环境的实验验证和统计检测
3.1 对实验结果进行检测的统计检验方法
对于得到的筛选结果,可以通过K-S检验和分位图(Quantile-Quantile Plot,Q-Q图)2种统计检验方法来检测是否服从特定概率统计模型。K-S检验是由俄国数学家柯尔莫格洛夫和斯米尔诺夫提出的一种拟合优度检验方法[23]。对于2个分布f(x)和g(x),一般设检验假设H0:f(x)=g(x);备择假设H1:f(x)≠g(x),如果H0=0,意味着接受原假设,即f(x)和g(x)是同分布;否则H0=1则拒绝原假设,即f(x)和g(x)不是同分布。H0的取值则通过在原假设条件下由样本数据计算得到的p值和显著性水平α的大小关系来决定。若p大于α,则接受H0;若小于α,则拒绝H0。其中,α通常取0.05或0.01等,这里取0.05。所以如果检测结果p大于0.05,则H0=0,说明筛选出的数据统计规律服从特定概率统计模型。
Q-Q图是通过比较2个概率分布分位数来对这2个概率分布进行比较的方法[24]。如果2个分布相似,则该Q-Q图分布在y=x的线上,如果2个分布线性相关,则Q-Q图分布在一条线上但不一定在y=x。此外Q-Q图也有可能呈现S型或弧形,S型则表明样本数据过分散或欠分散(正S型为欠分散,反S型为过分散),弧形则是由于极值的影响。因为实际物理模型要比简单的参数模型复杂的多,所以过分散和欠分散是数据统计分析中非常普遍的现象,这也使得S型的Q-Q图也非常普遍。对于检验结果,如果Q-Q图在一条线上,则说明筛选出的数据统计规律服从特定概率统计模型。如果呈现S型或弧形,是否同分布则要取决于其弯曲程度。
3.2 混响室中通过实验模拟衰落环境的统计检验结果
通过筛选算法成功从样本中筛选出了服从特定概率统计分布的数据并记录了筛选出数据的位置,在混响室同样场环境下获取新的一组数据,然后从相同位置处进行筛选得到新的一组筛选数据,并通过Q-Q图和K-S检验来对实验结果进行验证,实验图如图11~15所示。

图11 瑞利分布模拟实验的Q-Q图
根据Q-Q图的检测结果,在进行各种衰落模型模拟时,虽然大部分实验样本数据与期望分布样本数据分布在同一条线上,基本可以认为二者同分布,但还是发生了不同程度的过发散,而弯曲程度很难靠观察描述。这种图形化的方法判断不够精确,所以还需要K-S检验来进一步验证。从K-S检验结果(如表1所示)中可以看出,p值均大于0.05,H0均为0,成功地实现了瑞利分布、莱斯分布、Nakagami分布、对数正态分布和韦伯分布衰落模型的模拟。

图12 莱斯分布模拟实验的Q-Q图

图13 Nakagami分布模拟实验的Q-Q图

图14 对数正态分布模拟实验的Q-Q图
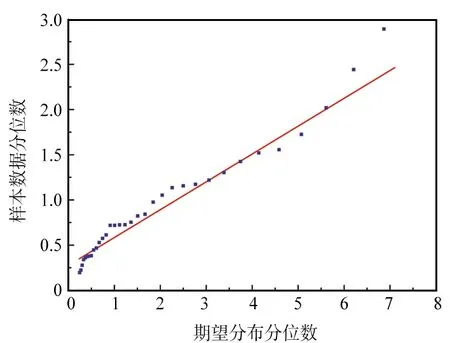
图15 韦伯分布模拟实验的Q-Q图
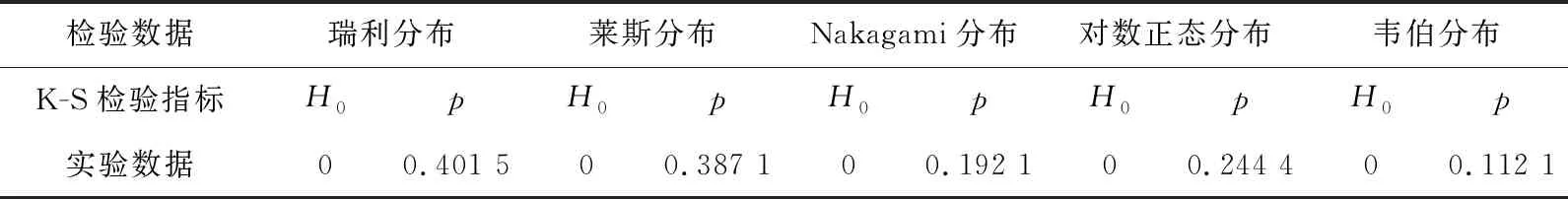
表1 K-S检验结果
4 结束语
本文提出了一种基于样本筛选的混响室内模拟无线通信中各种电磁衰落环境的普适性方法,通过该方法在混响室中实现了瑞利分布、莱斯分布、Nakagami分布、对数正态分布和韦伯分布衰落模型的模拟。这种混响室内可靠和可重复性的电磁衰落环境模拟为无线通信设备的测试提供了便捷、有效的途径。除了文中出现的几种衰落模型,基于样本筛选的这种新方法也对其他衰落模型具有普适性,可扩展到其他衰落模型,为无线通信中电磁衰落环境的模拟提供便利。

