基于单目视觉的水下机器人相对位姿精确控制

王晓鸣, 吴高升

基于单目视觉的水下机器人相对位姿精确控制

王晓鸣, 吴高升

(天津科技大学 机械工程学院, 天津, 300222)

针对水下机器人在实际作业中需要相对于特定的作业对象保持相对稳定且具有一定抗干扰能力的特点, 提出一种基于单目视觉位姿测量原理的水下机器人稳定性控制方法, 该方法的关键技术在于通过重投影法对水下机器人的三维位姿进行测量。以“观海ROV”为实验载体, 在实验水池中放置待观察目标, 利用水下机器人的前视摄像头作为单目视觉传感器, 建立实验验证系统。从实验结果所得到的位置数据表明: 采用基于单目视觉位姿测量原理控制方法的水下机器人能够在恒定水流冲击下相对于特定对象保持基本稳定, 可满足水下机器人在实际作业环境中的需求, 验证了文中方法的有效性。

水下机器人; 单目视觉; 三维位姿; 稳定性

0 引言

随着人类对海洋环境探测的不断深入, 水下机器人已成为开发和利用海洋资源的强有力工具。根据实际作业需要, 水下机器人相对于特定作业对象需要有一定的稳定性和抗干扰能力, 即依靠自身携带的动力系统在一定的水流作用下, 相对于作业对象保持一定位姿的能力。水下机器人保持自身的相对稳定性需要2个必要条件, 一是通过自身携带的传感器等元器件测量出机器人本体相对于作业对象的相对位姿; 二是根据测量出的相对位姿合理地进行水下机器人的动力分配。

传统的水下机器人主要用惯性导航系统作为位姿测量系统。惯性导航系统属于推算导航方式, 即从一已知点的位置根据连续测得的运动体的航向角和速度, 推算出其下一点的位置, 因而可连续计算出运动体的当前位置。但是惯性导航系统的定位误差会随时间增大, 长期使用时精度较差, 且每次使用前都需要花费较长时间校准[1]。水下摄像头作为传感器的创新产品, 具有体积小、局部定位精确等优点, 被广泛关注。

目前, 基于单目视觉的水下机器人稳定性研究已取得一定成果[2-4], 部分技术已通过实验室验证。唐旭东等[5]利用已知的管道模型, 以单目摄像头作为视觉传感器在实验室水池中进行了管道跟踪实验, 验证了单目视觉在水下环境中的可行性和有效性; 王鹏等[6]利用屋顶的结构光点设计了单目视觉位姿结算系统, 并通过实验验证了其有效性; 王中宇等[7]针对位姿求解过程中解不唯一的问题, 提出了一种新的单目视觉位姿测量方法; 高胜等[8]利用视觉反馈实现海洋环境下远程操作遥控水下航行器(remotely operated vehicle, ROV), 将自主式水下机器人的技术转移到ROV上, 减小了ROV操作人员的工作量; Trslic等[9]利用灯光作为位姿估算的基础, 将位姿估计技术用于水下机器人与对接站的自主对接中, 在北大西洋成功完成了海上实验并取得了显著效果; Shkurti等[10]提出一种综合计算机视觉和惯性系统的ROV状态估计算法, 该算法综合线速度、角速度、深度信息以及视觉信息估计ROV的六自由度姿态; Negahdaripour等[11]提出了一种基于图像马赛克的水下机器人定位方法, 利用光流场建立了视觉伺服系统; Wasielewski等[12]提出了一种基于特征的相机运动估计方法, 该方法需要提取和匹配相关特征; Zwaan等[13]采用光流和模板匹配等方法, 完成水下机器人的悬停实验。

总体来说, 国内外有关基于单目视觉的水下机器人相对稳定性研究主要包括2个方面: 一方面是模型已知的位姿计算, 该方法计算精度高、系统稳定性强, 便于水下机器人的控制, 但是该方法只适用于人工放置目标对象或者目标对象已知的场合, 存在一定应用局限性; 另一方面是模型未知的位姿计算, 该方法适用范围广、实用性较强, 但是相比前者精度不足, 只能粗略地进行位姿计算, 而且对于图像处理算法要求较高, 在实际应用中受到限制。

文中以全自由度小型ROV——“观海ROV”为载体, 从实际工程角度出发, 进行水下机器人稳定性研究。由于在实际工作环境中目标模型已知, 可以通过人工放置目标模型, 因此文中在传统算法的基础上设计了一种基于已知模型的位姿估计算法。该方法与传统基于已知模型算法不同的是[14]: 该方法选取基于目标对象上的4个特征点作为测量的基础, 利用其中3个点计算出可能的4个解, 再利用最后1个点分别对4个可能的解做重投影, 选取误差值最小的解作为最终结果, 称为重投影法。该方法基于最小的信息量即可求得位姿的线性解, 同时避免了非线性迭代的过程, 因此更能够满足实时性的要求。

1 实验系统组成

基于单目视觉的水下机器人稳定性实验的工作原理为: 通过人工布置的方式在水箱中放置待观察对象, 然后通过操作杆控制ROV, 使提前放置好的目标出现在ROV视场中, 以便提取出目标上的特征点。进一步通过计算机视觉的方法计算出ROV和目标之间的相对位姿关系, 并以此作为ROV动力分配的依据, 达到在一定水流作用下使ROV保持稳定的目的。

实验以“观海ROV”作为平台, 主要包括ROV本体和上位机系统。ROV本体以传统的摄像机作为视觉传感器实时采集水下画面, 采用八推进器非奇异结构布置形式, 其中水平和竖直方向分别有4个采用矢量形式布置的推进器, 完成机器人的前进、后退、上升、下降、左转、右转、横滚和俯仰的运动。上位机系统主要完成对ROV的图像采集、三维位姿计算和动力的分配, 工作流程如图1所示。图中可见, ROV实时采集水下图像并通过浮力缆传回上位机系统, 当观察目标出现在ROV的视场中时, 上位机采集特征点并计算出本体与目标之间的相对位姿关系, 以此作为控制量形成闭环系统, 进行ROV的动力分配, 使ROV相对目标保持稳定。

图1 实验系统工作流程

2 三维位姿计算

水下机器人在工作环境下可被当作具有六自由度的刚体, 将机器人所在坐标系称为相机坐标系, 将观察对象所在坐标系作为世界坐标系。三维位姿计算的实质是求相机坐标系和世界坐标系之间的位姿转化关系。理论上只需知道3个特征点分别在这2个坐标系下的坐标值, 就可计算出这2个坐标系之间的位姿转化关系。在实际工作环境中, 由于目标模型已知, 则特征点在世界坐标系下的坐标已知, 问题转化为求这3个控制点在相机坐标系下的坐标。在相机已经标定出内参的情况下[15], 可以计算出各个特征点与光心连线之间的夹角, 如果能计算出各个特征点到光心的距离, 就可求出特征点在相机坐标系下的坐标。综上所述, 三维位姿的计算主要包括3个过程:首先求出特征点与摄像机光心之间的距离; 然后根据求出的距离计算特征点在相机坐标系下的坐标; 再根据3个特征点分别在相机坐标系和世界坐标系下的坐标求2个坐标系的转换关系。

2.1 特征点与光心的距离

已知空间点的相对位置关系以及与光心连线的夹角, 则求空间点到光心的距离属于PnP (perspective-number-point)问题[16-17]。建立如图2所示的数学模型。图中,为相机光心,、和为3个控制点。

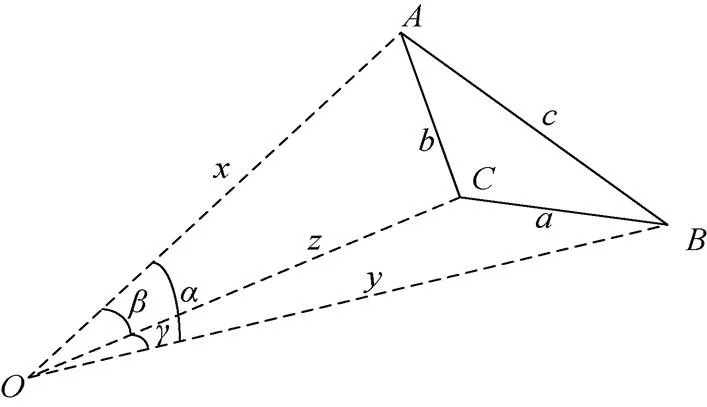
图2 数学模型示意图

根据余弦定理可知

式中:,分别代表光心与控制点,,之间的距离;,,分别代表控制点,,连线之间的距离;,,分别为光心与控制点,,连线之间的夹角。

该方程组为非线性方程组, 存在多解性和算法鲁棒性[18], 但是所有解必为以下4种情况之一[19]

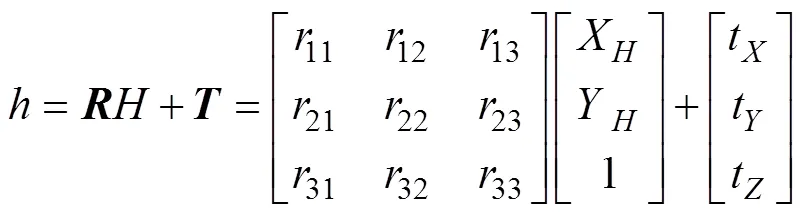
2.2 特征点在相机坐标系下的坐标

三维位姿计算第2步是求特征点在相机坐标系下的坐标, 为此建立投影模型(见图3)。

图3 投影模型示意图

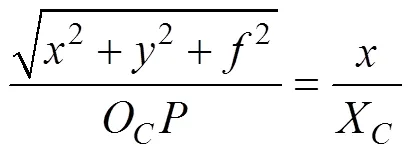
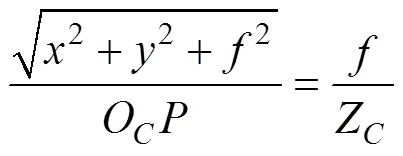
式中,代表相机焦距。

可得

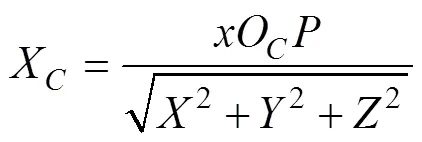
2.3 三维位姿计算

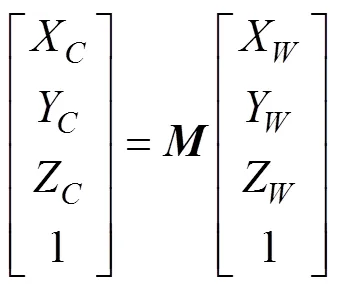
其中

映射变换可表示为

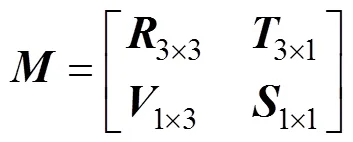
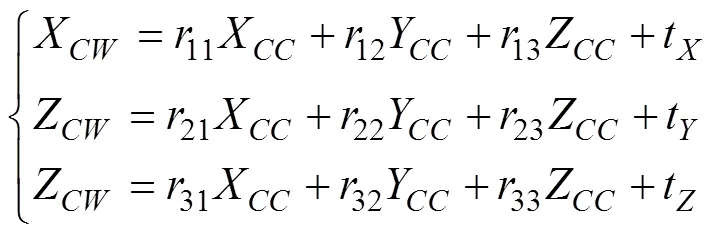
至此, 已经求出从相机坐标系转化到世界坐标系的旋转矩阵和平移矩阵, 得到相机坐标系和世界坐标系之间的位置转换关系, 就可以进行下一步的动力分配和运动控制。

3 控制策略

基于机器视觉的水下机器人相对位姿精确控制研究主要应用的场景是: 用户输入机器人与作业对象之间的位姿关系, 使得机器人相对于这个位姿关系保持稳定。当上位机采集到作业目标上的特征点时, 计算出水下机器人与作业对象之间的实际位姿, 并与用户输入的理想位姿作对比, 使水下机器人按一定的规律进行动力分配。当两者之间的差距较远时, 水下机器人以较快的速度运动; 当距离较近时, 水下机器人以较慢的速度运动。由于在水下环境中存在水流的影响, 当距离小于某个阈值时, 则认为达到理想位置。故选择传统的比例-积分-微分(proportion integration differentiation, PID)控制器作为控制方法, PID以其结构简单、稳定性好、工作可靠及调试方便成为工业控制的主要技术之一。

此处, 将理想位姿与实际位姿之间的误差值作为PID的控制量, 算出电机的动力分配方式

4 实验验证

为验证前文所述方法的有效性, 分别进行了位姿测量和ROV稳定性控制实验。在位姿测量实验中, 采用传统的迭代法和EPnP(efficient PnP)算法与前文所述重投影法进行了精度测量和运行速度测量实验, 并对结果进行比较; 在ROV稳定性测量实验中, 利用Whale 1214-Ⅱ推进器使水箱中的水处于不同运动状态, 然后观察使用此控制算法的ROV在不同转速下的稳定情况。

图4 PID控制流程

4.1 位姿测量实验

以红色标志点(见图6)为观察对象上的特征点并建立世界坐标系。实验中, 首先将待观察对象放至实验平台(见图5), 通过直尺测量相机光心大约在世界坐标系中的坐标约为(10, 30, 400)。待观察对象完全出现在摄像机视场后, 上位机系统会依次选择红色特征点进行位姿计算并输出位姿计算结果, 结果曲线如图7～9所示。

图5 位姿测量实验平台

图6 观察对象

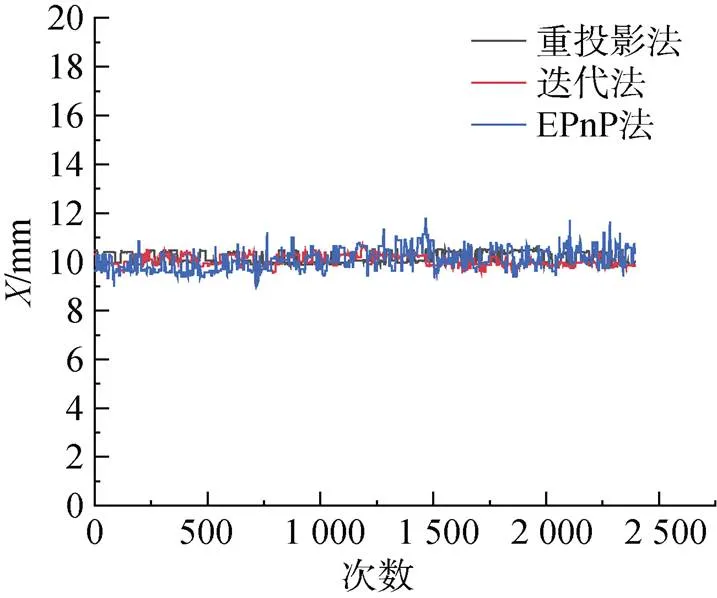
图7 X方向位姿计算结果曲线

图8 Y方向位姿计算结果曲线

图9 Z方向位姿计算结果曲线

由图中可以看出, 文中所涉及算法与迭代法计算结果都较为稳定, 误差能控制在一定的范围内, 而EPnP算法计算出的数值波动范围较大, 但是3种算法的计算结果都基本满足ROV在水下环境中的使用要求。

在运行速度测量实验中, 首先分别用3种方法进行1000次和10000次位姿计算, 从表1中可以看出, 进行1000次计算时, 迭代法平均花费时间为重投影法的10倍, EPnP算法花费时间与文中算法相近; 当进行10000次实验时(见表2), 迭代法的平均花费时间更长。为了进一步说明该算法在时间上的优势, 在相同的实验条件下用2种算法分别进行10次实验, 并且记录每次计算所耗时间, 结果如表3所示。

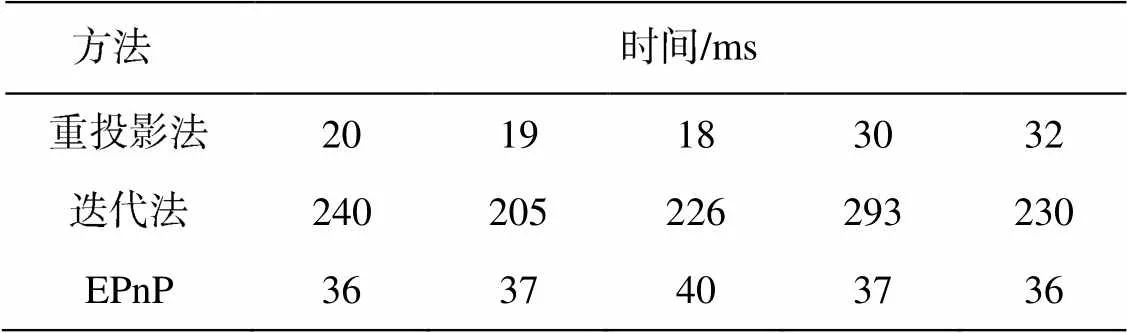
表1 1 000次实验计算时间对比

表2 10 000次实验计算时间对比

通过该实验可知, 文中的重投影法相比传统迭代法在满足相同精度的同时, 具有较快的计算速度; 而文中算法与EPnP算法相比, 计算结果更加稳定。在水下机器人行业中, 较快的计算速度能更好地满足机器人工作实时性的要求。

表3 单次实验计算时间对比

4.2 ROV稳定性测量实验

ROV的稳定性测试实验以“观海ROV”为载体(见图10), 在实验室的水池中进行。在水箱中安装Whale 1214-Ⅱ推进器来控制水箱中水的流速, 根据视觉系统测量的位姿信息, 利用PID形成闭环控制, 实现ROV的悬停实验。

图10 观海ROV

实验中首先调节Whale 1214-Ⅱ推进器至一定的转速, 使水箱中的水保持运动状态, 然后通过操控器操作ROV使待检测对象完全进入摄像机视场中(见图11), 上位机自动识别位于检测对象上特征点的位置, 并计算ROV与载体之间的位姿关系, 进而发出控制指令使ROV相对检测对象保持特定姿态, 观察ROV的运动情况。

图11 ROV视场

实验共3次, 分别为当Whale 1214-Ⅱ推进器转速为800、1 200和1 600 r/min时ROV的运动状态。实验时, 首先调节Whale 1214-Ⅱ推进器为既定的转速, 输入ROV与检测对象间距(方向)为200 mm, 即观察对象在相机坐标系中的坐标为(0, 0, 200), 然后输出两者之间位置变化情况; 等两者之间距离基本稳定之后, 再输入两者方向之间的位置为0, 即ROV始终正对观察对象, 并输出两者方向的位置变化。由于ROV本身携带有深度传感器, 能够进行深度控制(方向), 所以此处不存在深度方向上的数据。

图12～14分别为Whale 1214-Ⅱ推进器在转速为800、1200、1600 r/min时, ROV的位置变化情况, 其中为距离。从图中可看出, 随着Whale 1214-Ⅱ推进器转速的增大, ROV最终稳定状态的偏移量也越来越大, 当推进器转速达到 1600 r/min时, ROV到达稳定状态的偏移量最为严重, 但最终误差能够控制在一定范围内。实验结果证明了文中方法用于ROV控制的可靠性和可应用性。

图12 转速为800 r/min时ROV的位置变化曲线

图13 转速为1 200 r/min时ROV的位置变化曲线

图14 转速为1 600 r/min时ROV的位置变化曲线

5 结束语

文中从水下机器人的实际工程角度出发, 提出了一种针对特征点进行重投影的相机位姿计算方法, 详细说明了该算法的位姿计算步骤, 从理论上保证了该算法的可行性。位姿测量实验和ROV的稳定性实验表明: 文中方法除具有与传统位姿计算方法相同的精度外, 还可使ROV相对于特定的作业对象保持较强的稳定性和抗干扰能力。该方法目前仅在实验室的环境下进行了验证, 要真正应用于实际的作业环境中, 还需进一步提高算法的自动化程度和观察目标成像质量等, 从而提高整个系统的稳定性。

[1] 厉文涛, 聂晓明, 周健. 基于二维激光多普勒测速仪建立新组合导航系统的方法[J]. 中国激光, 2020, 47(3): 296-274.

Li Wen-tao, Nie Xiao-ming, Zhou Jian. Method for Establishing New Integrated Navigation System Based on Two- Dimensional Laser Doppler Velocimeter[J]. Chinese Jour- nal of Lasers, 2020, 47(3): 296-274.

[2] 魏延辉, 张皓渊. 水下作业型ROV定深控制系统的设计[J]. 中国科技论文, 2016, 11(8): 898-903.

Wei Yan-hui, Zhang Hao-yuan. Design of the Depth Control System for Underwater Work-class ROV[J]. China Sciencepaper, 2016, 11(8): 898-903.

[3] 徐凤强, 董鹏, 王辉兵, 等. 基于水下机器人的海产品智能检测与自主抓取系统[J]. 北京航空航天大学学报, 2019, 45(12): 2393-2402.

Xu Feng-qiang, Dong Peng, Wang Hui-bing, et al. Intelligent Detection and Autonomous Capture System of Seafood Based on Underwater Robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(12): 2393-2402.

[4] 周浩, 姜述强, 黄海, 等. 基于视觉感知的海生物吸纳式水下机器人目标捕获控制[J]. 机器人, 2019, 41(2): 242-249, 275.

Zhou Hao, Jiang Shu-qiang, Huang Hai, et al. Vision Based Target Capture Control for Sea Organism Absorptive Underwater Vehicle[J]. Robot, 2019, 41(2): 242-249, 275.

[5] 唐旭东, 庞永杰, 张赫, 等. 基于单目视觉的水下机器人管道检测[J]. 机器人, 2010, 32(5): 592-600.

Tang Xu-dong, Pang Yong-jie, Zhang He, et al. Underwater Pipeline Detection by AUV Based on Monocular Vision[J]. Robot, 2010, 32(5): 592-600.

[6] 王鹏, 赵汗青, 王江峰, 等. 基于单目视觉的相机位姿解算[J]. 电子科技, 2017, 30(12): 75-78.

Wang Peng, Zhao Han-qing, Wang Jiang-feng, et al. Based on Monocular Vision Camera Pose Computation[J]. Electronic Science and Technology, 2017, 30(12): 75-78.

[7] 王中宇, 李亚茹, 郝仁杰, 等. 基于点特征的单目视觉位姿测量算法[J]. 红外与激光工程, 2019, 48(5): 169- 176.

Wang Zhong-yu, Li Ya-ru, Hao Ren-jie, et al. Monocular Vision Pose Measurement Algorithm Based on Points Feature[J]. Infrared and Laser Engineering, 2019, 48(5): 169-176.

[8] 高胜, 陈昆, 张利巍, 等. 开架式观测型ROV定点悬停控制方法研究[J]. 石油机械, 2019, 47(2): 55-64.

Gao Sheng, Chen Kun, Zhang Li-wei, et al. Control Method for Fixed Point Hovering of Open-shelf Observational ROV[J]. China Petroleum Machinery, 2019, 47(2): 55-64.

[9] Trslic P, Rossi M, Robinson L, et al. Vision Based Autonomous Docking for Work Class ROVs[J]. Ocean Engineering, 2020, 196: 10684.

[10] Shkurti F, Rekleitis I, Scaccia M, et al. State Estimation of an Underwater Robot Using Visual and Inertial Information[C]//IEEE/RSJ International Conference on Intelligent Robots & Systems. SanFrancisco: IEEE, 2011: 5054-5060.

[11] Negahdaripour S, Xu X, Jin L. Direct Estimation of Motion from Sea Floor Images for Automatic Station-keeping of Submersible Platforms[J]. IEEE Journal of Oceanic Engineering, 1999, 24(3): 370-382.

[12] Wasielewski S, Aldon M J. Dynamic Vision for ROV Stabilization[C]//Oceans. USA: IEEE, 1996: 1082-1087.

[13] Zwaan S, Santos-Victor J. An Ocean Odyssey. Conference Proceedings Real-time Vision-based Station Keeping for Underwater Robots[C]//Oceans. USA: IEEE, 2001: 1058- 1065.

[14] Ferreira F. Comparing Region-based and Feature-based Methods for ROV Vision-based Motion Estimation[J]. IFAC Proceedings Volumes, 2012, 45(27): 91-96.

[15] 马宏伟, 王佐勋. 机械臂视觉相机标定的研究与仿真[J]. 齐鲁工业大学学报, 2019, 33(4): 57-63.

Ma Hong-wei, Wang Zuo-xun. Research and Simulation of Visual Camera Calibration of Manipulator[J]. Journal of Shandong Institute of Light Industry(Natural Science Edition), 2019, 33(4): 57-63.

[16] 郝颖明, 吴清潇, 周船, 等. 基于单目视觉的水下机器人悬停定位技术与实现[J]. 机器人, 2006, 28(6): 656- 661.

Hao Ying-ming, Wu Qing-xiao, Zhou Chuan, et al. Technique and Implementation of Underwater Vehicle Station Keeping Based on Monocular Vision[J]. Robot, 2006, 28(6): 656-661.

[17] Zhou Jie, Wang D K. Solving the Perspective-Three-Point Problem Using Comprehensive Gröbner Systems[J]. Journal of Systems Science and Complexity, 2016, 29(5): 1446- 1471.

[18] 王波, 胡浩, 张彩霞, 等. P3P问题多解现象的普遍性[J]. 中国科学: 信息科学, 2017, 47(4): 482-491.

Wang Bo, Hu Hao, Zhang Cai-xia, et al. Generality of the Multi-solution Phenomenon in the P3P Problem[J]. Scientia Sinica: Informations, 2017, 47(4): 482-491.

[19] 周鑫, 朱枫. 关于P3P问题解的唯一性条件的几点讨论[J]. 计算机学报, 2003, 26(12): 1696-1701.

Zhou Xin, Zhu Feng. A Note on Unique Solution Conditions of the P3P Problem[J]. Chinese Journal of Computers, 2003, 26(12): 1696-1701.

Relative Position and Attitude Precise Control of Underwater Robot Based on Monocular Vision

WANG Xiao-ming, WUGao-sheng

(SchoolofMechanicalEngineering, Tianjin University of Science and Technology, Tianjin 300222, China)

Aiming at the characteristics of underwater robots in actual operation, which they need to be relatively stable relative to specific operation objects and have certain anti-interference abilities, and a method for stability control of underwater robots based on monocular visual position and attitude measurement is proposed; the key technique of this method is to measure the three-dimensional position and attitude of the underwater robot using the method of re-projection. The “GuanHai ROV” is adoptedfor experimental verification, and the observation target is placed in the experimental pool. The forward camera of the underwater robot is used as a monocular vision sensor to establish an experimental verification system. The experimental results show that the position and attitude measurement principle based on the monocular vision control method of underwater robots can relatively specific objects under constant water flow remain stable, and can meet the needs of the underwater robot in the actual work environment; therefore, the method proposed in this study is effective for the precise control of underwater robot position and attitude. This research has greatly improved the stability of underwater robots in a working environment.

underwater robot; monocular vision; three-dimensional position and attitude; stability

TJ630.33; TB24

A

2096-3920(2021)03-0299-09

10.11993/j.issn.2096-3920.2021.03.008

王晓鸣, 吴高升. 基于单目视觉的水下机器人相对位姿精确控制[J]. 水下无人系统学报, 2021, 29(3): 299-307.

2020-08-05;

2020-10-21.

天津市教委科研计划项目(2017KJ022).

王晓鸣(1981-), 男, 博士, 副教授, 主要研究方向为机器人和嵌入式控制系统开发.

(责任编辑: 杨力军)