基于桥梁结构安全可靠性的车辆载重限值研究
朱 荣
(上海同济检测技术有限公司,上海市200092)
0 引言
桥梁的运营维护活动是形成对评估结果的管理对策。除了必要的加固维修以外,对不满足当前交通状况的桥梁进行适当的限载也是必要的管养手段。
欧美国家对桥梁通行汽车荷载限值问题的研究起步较早,并制定了符合其本国国情的车辆载重规制。其中,以美国的公路桥梁车辆载重标准体系最为完善。其基于应力超限率法,分别提出了FBF B、TTI和TRB等公式[1-2]作为美国评估规范中法定车辆荷载(Legal Loads)和限定车辆荷载(Posting Loads)的理论依据。
我国的车辆载重标准最早是1982年开展的“交通运输技术政策研究”。根据当时路网的技术状况,从1989年实施的《公路工程技术标准》规定了单轴重10 t的限值标准,并作为我国公路、桥梁设计的轴载标准和限载依据沿用至今。
经历30多年的发展,虽然超重运输现象严峻,但公路桥梁等基础设施条件有了明显改善。目前的道路超载认定却不能准确地为桥梁的限载取值提供可靠的依据,也不利于合理地提升公路桥梁服务水平。为此,国内学者在超载桥梁安全性分析和限载方法等方面开展了相关的研究[3-4],虽取得了一定的研究成果,但也存在一些不足之处:(1)未能提供桥梁结构安全的限载分析指标,合理的安全指标是构建桥梁限载分析的重要前提;(2)并没有提出比较完善的限载分析理论,为在役桥梁安全管养提供合理的理论依据;(3)未能形成典型限载车型谱系,为桥梁限载管理提供现实依据。
现通过对实测车辆数据的统计,分析现阶段货车类型及其荷载分布特征,根据各载重车辆的超载情况和对桥梁结构的影响确定桥梁限载的典型车型。然后,以结构可靠性理论为基础,对基于桥梁安全运营的车辆载重限值分析方法进行研究,明确计算基本步骤。最后,通过算例,介绍本文提出的在役桥梁限载分析的实施过程。该项研究从桥梁结构安全运营的角度建立了车辆限载取值的方法,为重载交通下的桥梁管养提供理论依据。
1 车辆荷载调查及典型限载车型谱系
1.1 运营阶段车辆荷载特性
车辆荷载特性包含车重、轴重和轴距在内的描述车辆基本信息参数,是桥梁汽车荷载分析的重要参数,由一些典型车型构成。参考我国汽车制造行业标准,常见的货运车型大致可以划分为10种型式,按轴数分类主要包括二轴、三轴、四轴、五轴和六轴等五种类型[5]。通过对车辆荷载数据进行的统计,可充分了解当前路线上的主力车型,各车型构成情况见表1所列。

表1 车型分类及车型组成特性一览表
可以看出:绝大多数的货车以二轴和六轴车为主,两者总和接近所有货车总量的3/4,其中二轴货车占48.9%,六轴车占23.7%;三、四轴车代表车型包括自卸车和仓栅式载货车,占比不大,分别为10.5%和12.5%;五轴车所占比例最小,仅为4.4%,代表车型为装载能力较小的拖挂车,主要用于重量较轻的货物运输。
各车型的车重和超载情况的统计见表2所列,超载车辆的认定基于目前国内的治超标准[6],车辆超载率按照式(1)计算:

从表2各车型的车重和超载情况分析看,六轴车的两种车型T-9和T-10,以及五轴的T-6超载车比例较大,且超载问题严重,是重型货车中需重点关注的车型;对于中型载重车,需重点关注四轴的T-4和三轴的T-3车型;虽然两轴车整体车重水平不高,但由于轴数较少,分担到单轴的重量较大,对于小跨径桥梁,过重的轴载也会带来极大的安全隐患,因此,二轴货车也需要考虑。

表2 车重和车辆超载情况一鉴表
1.2 典型限载车型谱系
典型限载车型是桥梁限载分析的前提基础,表1所列代表了目前公路通行的大部分车型,由于车型类别较多,用于桥梁限载分析是相当繁琐的。为此,需要进行简化,提炼出一组最具代表性的车型,以此形成桥梁限载的车型谱系。
目前,车辆限载标准的普遍做法是根据轴型车辆(轴数)限制车重。现参考这种限载方式,具体方法如下:
首先,将表1中的10类车按轴数进行归类,对具有相同轴数的车辆,综合考虑其数量比例、车重及超载情况和对结构荷载效应等因素,确定一种最具代表性的车型作为限载模型车辆。
例如,四轴车有T-4和T-5两种车型,其荷载特性的比较见表3所列。从表3可以看出,T-4车型在数量上五倍于T-5,平均车重与超载车比例均大于T-5;而在平均超载率和最大超载率上,T-5略大10%左右。

表3 四轴车T-4、T-5车辆荷载特性比较一览表
对比两种车型在相同车重下的简支梁跨中弯矩和支点剪力效应,如图1所示。从图1可以看出,在相同车重下,车型T-4通过桥梁产生的荷载效应大于T-5,说明四轴车中T-4轴重和轴距配置对结构受力不利。综上分析,选择车型T-4为四轴车的限载模型车辆。
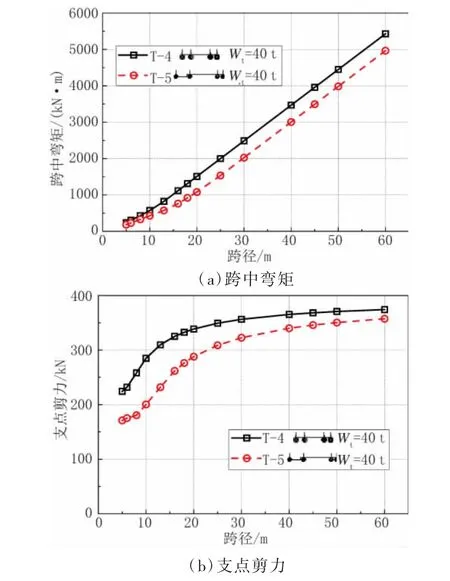
图1 T-4、T-5简支梁效应比较图(车重Wt=40 t)
其次,确定各代表限载车型的轴距、轴重与总重的分配关系。轴距根据表1统计结果获得;轴重分配比例利用实测数据中的总重和轴重数据通过线性回归分析法确定。以T-4车型为例,图2为该车型轴重与车重关系的线性回归图。

图2 T-4车型车重与轴重的关系图
从图2可以看出,轴重线性回归拟合的可决系数R2在0.75以上,说明轴重与总重比例关系与线性函数评价之间的相关性较好。最终,得到四轴车型的轴重分配比例为0.14∶0.16∶0.35∶0.35。
最后,按照与设计荷载效应等效的原则确定每类模型车辆的标准额定车重。选取公路-I级汽车荷载作用下,中小跨径桥梁跨中弯矩或支点剪力效应标准值为等效的荷载效应,计算公式为:

式中:WQ为模型车辆额定车重;MD为公路-I级汽车荷载作用下的荷载效应标准值;Mu为模型车辆在单位车重下的荷载效应。
根据上述方法,将表1轴数相同的各类车型进行合并,重新定义成5个车型类别组成的限载车辆谱系,如表4所列。为了使模型车辆的荷载参数简洁和应用上的方便,车辆轴重取5kN的整数倍,轴距取0.1 m的整数倍。

表4 限载模型车辆额定荷载谱系一览表
2 基于安全可靠性的车辆载重限值分析方法
2.1 载重限值的可靠性分析方法
结构的可靠性反映的是结构的承载能力与荷载效应间大小的随机比较,用概率的方法来描述结构完成预定功能的能力。对于既有桥梁的汽车限载分析,是根据预设的目标可靠度和已知的结构承载能力和恒载效应反算出允许通行的最大汽车荷载效应,属于可靠性反问题的范畴[7]。
所谓可靠性反问题,可以看作是在指定可靠指标的前提下,求解极限状态方程中影响结构的随机变量统计参数,这些统计参数通常包括随机变量的均值或标准差。
对于给定的目标可靠指标βT和极限状态方程G(x)=0,X=(x1,x2,…,xn-1,ξ)是由若干个服从任意分布且相互独立的随机变量,U=(u1,u2,…,un-1,uξ)为通过当量正态化后的标准正态分布变量,其中ξ为待求的随机变量。可靠性反问题可描述成为求解随机变量ξ的参数(均值μξ或标准差σξ),使满足:

用JC法进行可靠度分析时,可靠指标定义为标准正态空间内坐标原点到极限状态曲面的最短距离,将极限状态功能函数在U*(验算点)进行Taylor级数展开,近似地取一阶项,为:


验算点u*的诸坐标表达式为:

其中,cosθui为法线OU*对坐标向量的方向余弦:
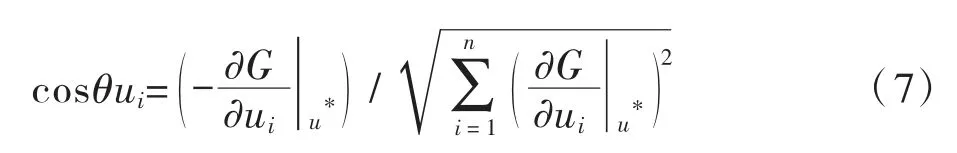
给定U和ξ的初始值U(0)和ξ0,设ξ为待求参数,将极限状态方程在初值ξ0处进行Taylor展开,仅保留一次项:

由上述公式求得一个新的向量U(i),同时满足继而得到新的ξ值,重复式(8)和式(9)的计算过程,直至U和ξ全部收敛。
参照可靠性反问题的求解方法,车辆限载取值的计算步骤总结如下:
(1)确定结构构件限载分析的抗力R和恒载效应SG的概率分布和统计参数、汽车效应SQ的概率分布类型、变异系数δQ与平均值系数KQ,并给定目标可靠指标βT;
(2)将抗力及荷载效应随机变量进行当量正态化,转换为标准正态空间下的随机变量;
(3)在规定的作用效应组合下,建立极限状态方程,按照上述单参数可靠性反问题的计算方法,求解出汽车效应平均值μQ;
(4)由公式SQ=μQ/KQ求得汽车效应标准值SQK,P,最后,根据SQK,P确定各限载车型的车重限值WP。
一般认为,车辆的轴重与总重保持一定的比例关系不变,即典型限载模型车辆的荷载效应与其车重成线性关系。基于这一假定,已知典型限载模型车辆的荷载效应SQ,即公路-I级荷载标准值效应,引入限载系数ξq=SQK,P/SQ,通行车辆的限载值WP按下式进行计算:

3.2 在役桥梁的车重限值分析方法
与在役桥梁评估相似,车辆限载分析应体现运营桥梁的“在役性”特征,即要体现桥梁的自身技术状况,还需考虑管理者对桥梁的管养需求。管养需求一方面反映结构在运营中必须满足的使用性能要求,同时又符合管理者对运营风险的承受能力,并受投资效益的制约。就安全和经济两方面而言,管养需求可表征为可靠指标的合理选取。
可靠指标的大小反映结构失效风险水平。在现行设计规范中,可靠指标一般在2.0~5.0范围内进行取值,以满足不同失效后果和安全措施成本的结构构件功能要求。就限载取值而言,可以预计,较大的可靠指标,使车辆的限载取值小,结构的运营风险减小,维护费用降低,线路运输经济效益降低;反之,车辆的限载取值大,虽增加经济效益,但增加结构的失效概率、增加维护费用。
实际上,在役桥梁车辆限载主要是保证结构运营的安全性问题,因而,可靠指标取用可与结构设计或安全性评估要求相一致。对已运营一段时间的在役桥梁,根据自身结构的技术状况,和特定的交通荷载环境,设置不同的目标可靠指标。因此,现建议:
对于技术状况良好,且能满足当前交通通行需求的桥梁,从结构耐久性和减少维护成本上考虑,宜维持设计的可靠指标。
对于技术状况较差,不能满足当前通行要求的桥梁,在保障运营安全前提下,适当降低结构使用要求,使运输经济效益最大化,建议在设计可靠指标上减1.0。
对于特定桥梁车辆限载分析步骤总结如下:
(1)确定限载分析的效应模式,如抗弯、抗剪等。
(2)在规定的作用效应组合下,建立极限状态方程,并给定限载目标可靠指标βT。
(3)通过对结构的检测和计算分析,确定结构在当前状况下的承载力Rnd,抗力R和恒载效应SG的概率分布和统计参数,活载效应SQ的概率分布、变异系数δSQ与平均值系数KSQ。
(4)利用可靠性反问题的计算方法,求解出满足目标可靠指标βT的活载效应平均值μSQ,由公式SQK=μSQ/KSQ求得汽车效应标准值SQK,最后,根据SQK确定各限载车型的车重限值WLV。
4 算例分析
某16 m钢筋混凝土简支T梁,横向布置5片T梁,计算跨径15.5 m,设计荷载等级为公路-I级。主梁采用C30混凝土,纵向主筋采用HRB335级钢筋。桥梁的横向断面构造如图3所示。

图3 16 mT梁跨中横断面图(单位:cm)
选择跨中截面正弯矩为控制效应,抗力和效应的概率模型及参数可以根据检测结果经计算得到,计算方法可参考相关文献[8,9],本文不再赘述。抗力和效应的概率模型和统计参数见表5所列。
分别按照设计要求的目标可靠指标βT=4.7和降低结构使用要求βT’=3.7进行限载。计算得到各片梁满足限载可靠指标的汽车荷载效应标准值SQK,P,见表6所列。
从表6数据可以看出,边梁T-1的状况最为不利,根据设计汽车荷载效应标准值SQ(见表5),计算得到最小限载系数ξq分别为1.13和1.52,由此确定车型的车重限值见表7所列。对于六轴拖挂车,允许的最大车重分布为620 kN和835 kN。

表5 抗力和效应统计参数表

表6 限载汽车效应计算表
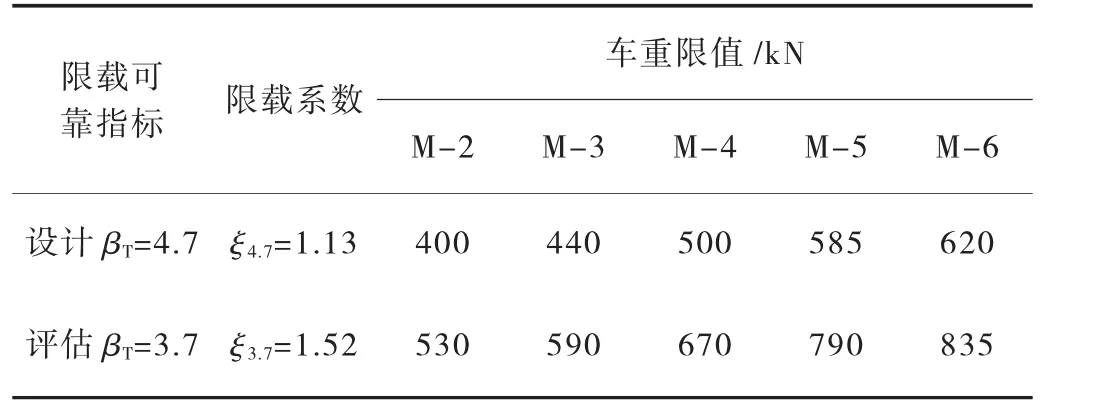
表7 16 m简支T梁车重限值表
4 结论
从桥梁结构安全运营的角度,利用可靠度反问题的求解方法,提出了桥梁限载分析方法及限载车辆荷载模型。主要的研究结论如下:
(1)通过实测的车辆荷载数据统计,分析了载重车辆组成及车重与轴重分布特征。根据车型比例、车辆超载情况,以及轴组配置等因素对结构响应的影响,按轴型分类建立了桥梁限载分析的典型车型谱系。
(2)基于可靠度反问题的求解方法提出了桥梁限载分析方法,引入限载系数表示限载车重与设计汽车荷载之间的关系,并建立了在役桥梁安全运营的车辆限载分析步骤。
(3)通过算例,介绍了本文提出的在役桥梁限载分析的实施过程。结果表明,本文提出的车辆载重限值的取值方法能够很好地体现结构可靠性思想,对桥梁限载决策的制定更具有科学的指导意义。

