综合管廊燃气舱结构形式对燃气爆炸超压的影响*
夏 微,高 魁,2,乔国栋,田 宇,周云权
(1.安徽理工大学 安全科学与工程学院,安徽 淮南 232001;2.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南 232001)
0 引言
城市地下综合管廊是1种集约式的管线建造模式,其内部综合了给排水、电力、燃气、供热、通信等各种市政管线和设施[1]。燃气管道泄漏会引起火灾、爆炸、中毒等恶性事故,由此带来的损失是不可估量的。
万留杰等[2]研究燃气舱内的甲烷浓度分布得出浓度分布与泄漏位置及风速有关;袁欣然等[3]得出燃气以波峰波谷的形式对称扩散,泄漏口位置在防火分区中心最危险;刘希亮等[4-6]研究管廊在燃气爆炸作用下的动力响应;张书豪等[7]提出维护管廊的安全仅靠通风是不合理的,还要结合截断和放散措施;王玉琪[8]分析综合管廊内燃气泄漏扩散的相关问题,同时研究综合管廊内的燃气爆炸问题;孙加超等[9]模拟综合管廊燃气舱在不同爆炸荷载下的爆炸情况,获得管廊的破坏模式、各测点的超压时程曲线和超压峰值曲线;田威等[10]通过数值模拟研究燃气舱在1,5,20,40 kg TNT药量下的内爆情况;朱邵飞等[11]对巷道内的瓦斯爆炸进行数值模拟研究,分析冲击波衰减变化规律;Zhu等[12]提出1种表征截面的方法,并发现不同截面隧道中不同长度的甲烷-空气混合物的最大峰值超压,呈现各种形式,从驼峰形状到波浪状和碗状;Li等[13]研究隧道内爆炸冲击波的强度和传播特性,并分析爆炸冲击载荷作用下衬砌的有效应力和动力响应;刘中宪等[14]得出在燃气爆炸荷载作用下,管廊衬砌的损伤破坏具有局部性和弱传递性。
文献调研发现,多数学者对综合管廊燃气舱的研究主要集中在燃气泄漏扩散和燃气爆炸对管廊结构的破坏影响等问题,而对燃气在管廊内爆炸产生的冲击波的传播规律的研究较少。因此本文采用模拟软件Fluent19.0对不同结构下的管廊燃气舱爆炸冲击波传播特征进行数值计算,揭示不同情况下爆炸过程中的超压变化规律。
1 模型参数
1.1 模型设置
燃气舱简化几何模型如图1所示。简化燃气舱为密闭狭长空间,选取燃气舱的1个通风分区进行研究。通过改变高度、长度、局部开口情况进行研究。采用二维模型进行计算,使用结构网格进行网格划分,网格尺寸为0.1 m×0.1 m。湍流模型选用RNGk-ε模型,燃烧模型选择涡耗散模型。采用Pressure-Based,PISO算法求解。
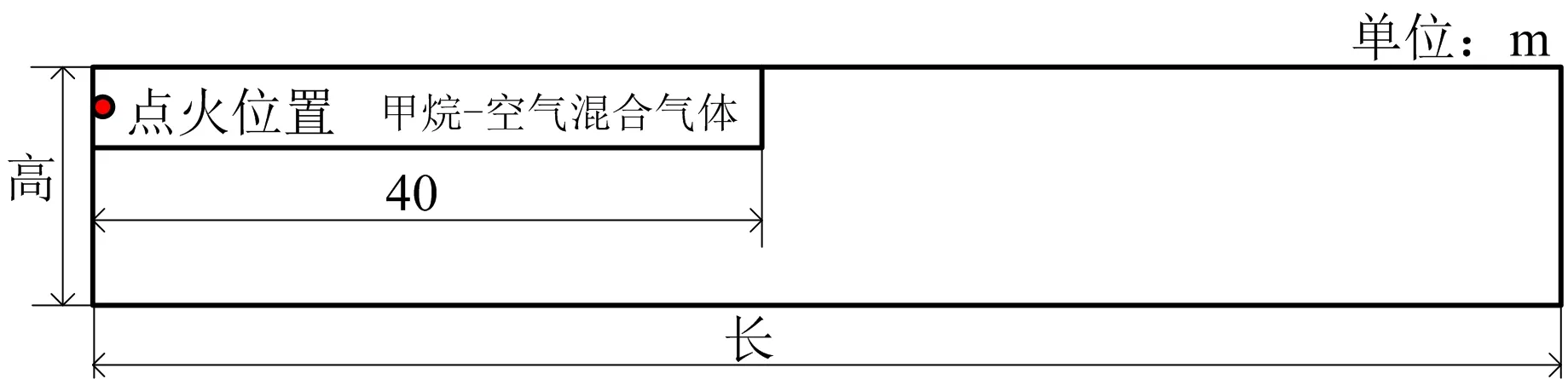
图1 简化几何模型
对模型做出如下假设:
气体满足理想气体状态;燃气舱墙面为刚性,不考虑流—固耦合作用;系统绝热,与外界无热交换;燃气爆炸过程为单步反应。
燃气爆炸冲击波传播的气体动力学过程涉及到质量守恒、动量守恒、能量守恒及燃料组分方程[15]。
1.2 初始条件及监测点设置
爆炸气体为甲烷空气混合气体,甲烷体积分数为9.5%。由于甲烷密度低于空气密度,因此甲烷气体会聚集于燃气舱顶部。为便于计算,将甲烷-空气混合气体简化为浓度均匀的矩形,设置积聚长度为40 m,高度为2 m。点火位置位于燃气舱模型的左端。每隔10 m在距燃气舱顶部1.25 m处设置监测点。
2 数值方法验证
为验证数值模拟方法的可靠性,搭建实验装置进行实验,同时模拟实验条件进行数值计算。实验管道长18 m,在管道中心布置5个测点,距离点火端的水平距离依次为9.5,11.5,13,13.5,15.5 m。采用部分管道填充甲烷空气预混气体,部分管道充入空气进行实验,点火端闭合,另一端开口。实验中填充11 m长度的甲烷空气预混气体,通过传感器和数据采集系统获得各个测点的爆炸超压。实验装置如图2所示。

图2 实验装置示意
实验及数值计算所得出的超压峰值变化曲线如图3所示。结果表明数值计算结果与实验结果的变化趋势是一致的,随着传播距离的增加,两者间的误差增加,最大误差不超过10%。模拟所得超压峰值大于实验数值,这是由于在数值计算中假设模型绝热,计算条件较为理想。在真实实验情况中会由于实验系统与外界的热交换及实验仪器精密度等原因,导致监测数值变小。

图3 超压峰值变化曲线
3 结果与分析
3.1 燃气舱高度对爆炸超压的影响
建立长为200 m、高度分别为2.5,3,3.5,4 m的数值模型进行计算。不同测点的超压变化曲线如图4所示。点火后,燃烧波形成,燃烧波压缩未燃气体形成压缩波,多道压缩波追赶叠加形成冲击波。冲击波从点火端开始向外传播,各个测点的超压从左到右依次上升到达第1个峰值;前驱冲击波通过后,超压值下降;随后前驱冲击波后的压缩波到达测点,使得测点的超压值再次小幅上升,之后下降。由于燃气舱通风分区两端封闭,因此当前驱冲击波传播到右侧时会被反射形成反射波,距离封闭端较近的测点会因冲击波与反射波的叠加作用从而使超压值突跃至峰值,如图4(c)所示。冲击波会在燃气舱内多次反射,因此超压变化曲线整体呈现先增加再减小再增大反复振荡变化的现象。冲击波到达测点时间随着燃气舱的高度的增加而增加,表明冲击波的传播速度随高度的增加而减小。

图4 不同测点超压变化曲线
冲击波传播时各测点的超压峰值如图5所示。图5表明同一测点的超压峰值随着燃气舱高度的增加而减小,燃气舱的高度为2.5 m时,10 m处的测点超压峰值为858.661 6 kPa,约为高度为4 m时的2倍。高度的减小使得火焰向前传播时湍流增强,增加未燃气体与火焰的接触面积,促进分子之间的碰撞,从而提高反应速率,使得超压峰值增加。随着高度的增加,超压峰值曲线由“驼峰状”逐渐变为两端高中间低的“盆形”,产生最大超压的位置转移到接近点火源的位置。燃气舱高度对冲击波传播过程中产生的最大超压的影响如图6所示,随着高度的增加,爆炸过程中产生的最大超压逐渐减小,最大超压与高度呈反比关系。

图5 超压峰值变化曲线
3.2 通风分区长度对爆炸超压的影响
对燃气舱高为3 m,通风分区长度分别为100,200,300,400 m的情况进行研究。不同长度通风分区情况下,超压峰值变化曲线如图7所示。不同通风分区长度情况下,同一测点的超压峰值重合,说明增加通风分区长度不会加剧燃气的燃烧反应。通风分区长度分别为100,200,300 m时,超压峰值曲线呈现先减小后增大的趋势,均在燃气舱后段产生突跃,这是由于封闭端产生反射波与冲击波的叠加作用影响。通风长度为400 m时,超压峰值在340 m处接近0 kPa,说明在340 m处气体爆炸产生的冲击波衰减为声波,不会在右端防火门处产生突跃。随着长度的增加,产生最大超压的位置由右端封闭位置转移到点火端。长度对最大超压的影响如图8所示,爆炸过程产生的最大超压随着通风长度的增加先减小后维持平稳。延长通风分区并不会增加爆炸过程中的最大超压,因此可以在考虑防火的要求下根据实际情况适当延长通风分区的长度。

图7 不同长度通风分区超压变化曲线
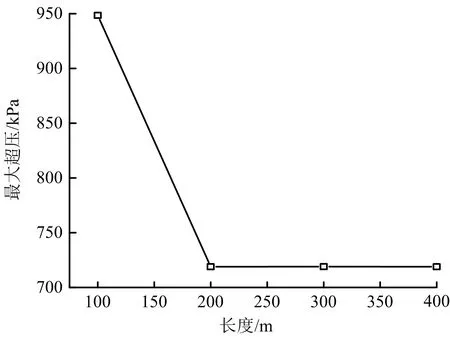
图8 长度对最大超压的影响
3.3 燃气舱局部开口对燃气爆炸超压的影响
建立燃气舱局部开口模型进行数值计算。燃气在局部开口和封闭情况下,不同测点的超压变化曲线如图9所示。由图9可知,局部开口情况下产生的超压小于封闭情况下。观察超压峰值产生的时间可知,封闭情况下冲击波的传播速度大于开口情况下。局部开口情况下燃气舱封闭端产生的反射效应对超压值的影响较小,以测点19为例,封闭情况下经反射叠加后的超压值约700 kPa,约为2 m开口情况下的2.8倍。不同开口情况下超压峰值变化曲线如图10所示。不同情况下超压峰值曲线的变化趋势相同,随着距离的增加,先减小后增大。10 m处,三者的超压峰值较为接近,随后由于局部开口泄压的影响,开口情况下的超压峰值均低于封闭情况下的超压峰值。随着局部开口大小的增加,封闭端冲击波的反射叠加效应逐渐减弱。
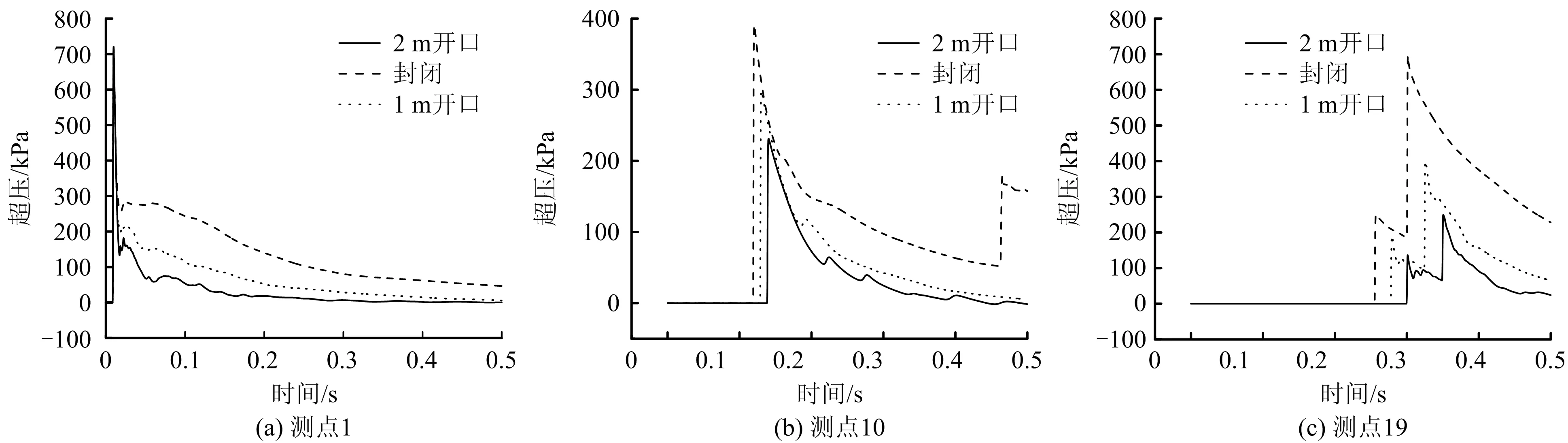
图9 不同测点超压变化曲线
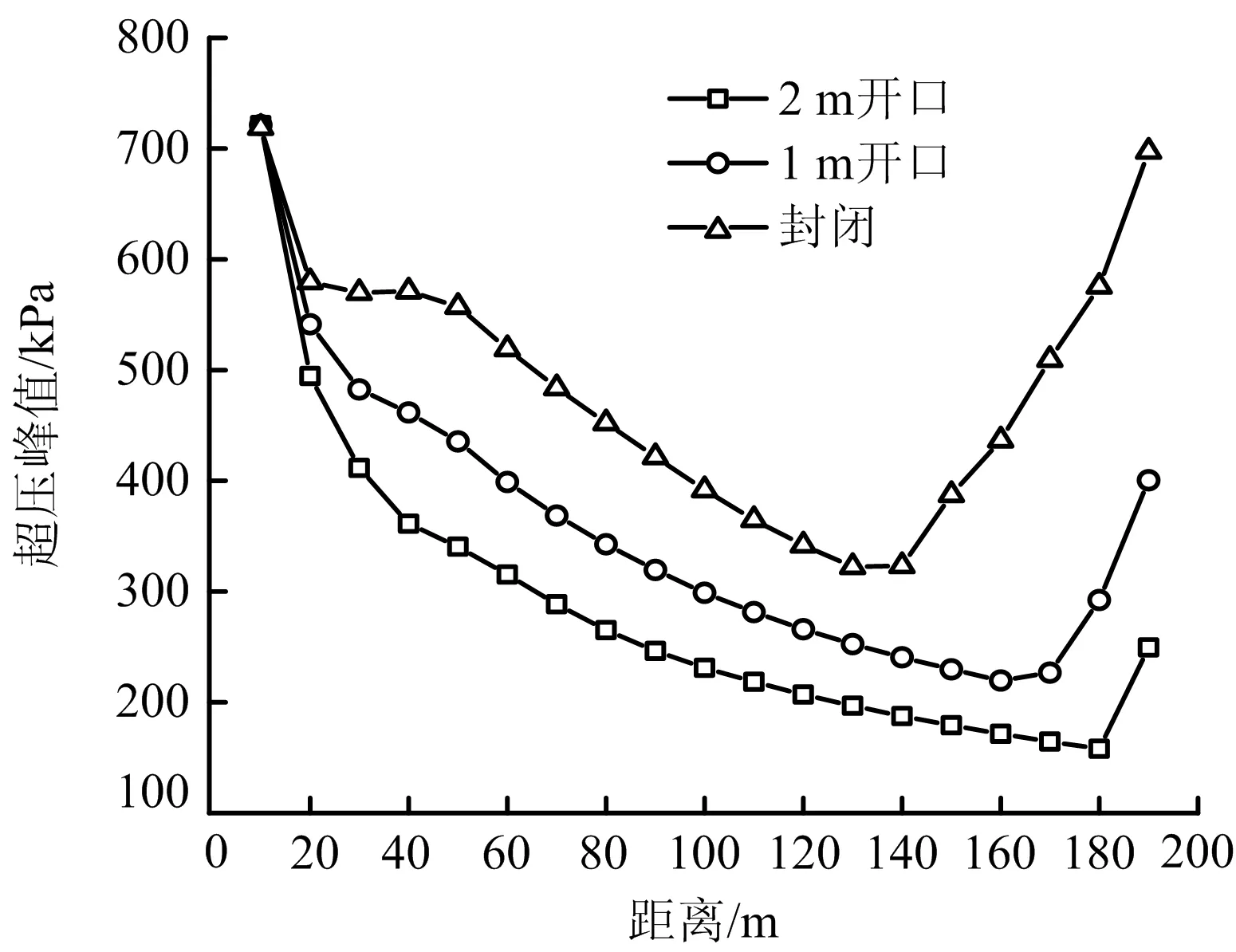
图10 不同开口情况超压峰值变化曲线
4 结论
1)随着燃气舱高度的增加,超压峰值曲线由先增再减再增的“驼峰状”变为先减小再增大的“盆形”。爆炸过程中产生的最大超压随高度的增加而减小,最大超压与高度呈反比关系。由于冲击波反射叠加效应的影响,封闭端产生的超压较高。建议结合实际工况中,对燃气舱高度进行合理设计并加强封闭端强度。
2)对不同通风分区长度情况下的超压变化进行分析,发现长度为100,200,300 m时超压峰值先减小再增加。长度为400 m时,超压峰值在340 m处接近0 kPa,气体爆炸产生的冲击波衰减为声波。爆炸过程产生的最大超压随着通风长度的增加先减小后维持平稳。延长通风分区并不会增加超压峰值,因此可以在考虑防火的要求下根据实际情况合理确定通风分区的长度。
3)局部开口的存在使得爆炸气流能够自由泄压。开口大小影响爆炸强度。同一测点,超压峰值随着开口的变大而减小。结果表明,开口越大,泄压效果越好,但由于泄压会影响到管廊的外部环境,建议实际情况中应考虑管廊的外部情况,确定燃气舱的开口情况。

