线性反馈移位寄存器的设计与仿真

张 州

(黑龙江生态工程职业学院 智能装备学院，黑龙江 哈尔滨 150025)

数字集成电路测试系统中有对微型处理器的测试。半导体储存电路的测试以及其他类型的电路测试。在测试的过程中可以依靠测试系统器材的功能和相关的测试配置，以及相关的脚本电子电路对测试电路进行合理科学的配置测试[1]。为了在降低成本的同时提高测试质量，提出了可测性设计。可测试性是指在设计阶段加入功能设计以外的逻辑，用以支撑后续芯片的生产测试。其中可测性设计中关键的一项低成本测试技术是内建自测试，指系统和设备能够自行准确、及时地确定系统和待测设备工作的状态能否工作，工作性能是异常还是正常，并将其电路内部故障隔离的一种特性。可测试性是集成电路或设备自身的一种设计特性，描述测试集成电路时测试信息获取的难易程度的表征[2]。在满足且保证芯片可以运行正常功能的基础上，通过加入有效的测试电路在被测电路中，使芯片的测试时间与测试难度有效降低，从而使其成本也随之降低。可测性所指的并不是产品可不可测，而是指产品测试难易与否[3]。

1 研究内容

采用内建自测试的方法进行测试研究，通过此方法对仿真结果进行分析和比对，从而验证设计的可行性。本文主要设计5阶LFSR线性反馈移位寄存器。此移位寄存器结构简单，运行速度快，其结构分为内接型(IE)和外接型(EE)。通过设计5阶EE型基于原多项式线性反馈移位寄存器，并利用ModelSim仿真软件完成仿真测试，从而验证其是否可生成M序列，对比可生成伪随机序列的寄存器与可生成M序列的硬件结构，来验证原多项式及其互补多项式均可生成M序列。

2 线性反馈移位寄存器的技术问题

2.1 VLSI测试技术

VLSI测试是确保由合成设计制造的物理设备没有制造缺陷的一个步骤。要保证产品无缺陷，不仅仅是看测试技术是否成熟、测试装置是否有效，而且还涉及到电路和系统的设计、模拟和验证、制造等诸多过程，只有将集成电路的所有步骤中的问题都变小并解决才能保证产品的质量[4]。所以即便集成电路测试技术在集成电路的生产制造过程中有着重要且不可忽视的地位，但其他步骤也尤为关键，相比之下测试问题还是重中之重。测试集成电路不仅要测试电路的质量，还要缩短芯片的测试时间来提升效率，还要以合理的方式来降低成本，所以集成电路测试技术己经成为集成电路领域的研究重点[5]。在电路中加入可测试性设计功能结构齐全的电路来测试集成电路是否存在故障缺陷。可测试性设计(Design For Testability,DFT)针对芯片测试中出现的问题，寻求解决方案，这是测试芯片中的一个极为重要的环节[6]。

2.2 测试故障模型

集成电路在生产制造过程中，很可能由于外来的因素导致部分芯片产生物理缺陷(Defect)。外界环境就是一个很大的因素。由于外界环境不够纯净或者电路的密封泄露，很容易使集成电路表面掺杂垃圾、杂质，即生产的硬件与预期设计之间存在差异，比如说寄生晶体管。这种晶体管是一种半导体，它将各种小的晶体管组合在一起合并成一个电器元件，它自身带有电容，在高频的条件下，由于寄生晶体管的数量之多，晶体管之间会相互影响，使电路的运行速度变慢，从而也对电路本身造成了不必要的能量损失[7]。这些类似的问题有很多。这些缺陷不仅会对电路造成影响，还会引起系统运行出错，进而导致系统失效(Failure)。针对这些缺陷，通常将其抽象建模成故障模型(Fault Model)来表示。在检测故障模型的过程中，会有一些常见的故障问题，包括固定故障(Stunk-at Fault,SAF)、跳变故障(Transition Fault,TF)和时延故障(DelayFault, DF)等。其中固定故障是在集成电路中表现得最为广泛的一种，它是一种门级故障模型，常用的是单固定故障(Single Stuck-at Fault,SSA)，将逻辑门固定在逻辑0或者逻辑1，逻辑状态不发生变化。

2.3 边界扫描测试

边界扫描测试方法在集成电路领域格外受到关注。简单地说，边界扫描就如同电脑扫描病毒一样，对计算机内部的各个文件进行检测，把报告发送给我们。边界扫描测试技术与之几乎相同，是对整个系统内容进行扫描并得到信息反馈,从而验证测试的准确性来获取测试结果。它是把扫描路径法扩展到整个集成电路板级或系统级，通过对整个电路的扫描反馈来对电路进行检测。边界扫描电路有两点好处：一是有助于对整个集成电路系统的故障进行定位，找到问题所在，并且能通过扫描来测试路径是否顺畅，检测芯片与芯片之间引脚的链接是否完好，提高了芯片的检测速度；二是可以将预先设定好的程序检测功能内置好，通过边界扫描测试方法来使整个集成电路芯片完成特定的功能测试，使整个系统变得更加灵活可控[8]。基于边界扫描设计法所涉及到的元器件，与外部进行串行通信交换信息，允许测试指令及相关的测试数据串行送给元器件，然后通过元器件，从元器件中串行读出测试指令的执行结果来完成测试，这就是边界扫描的含义。

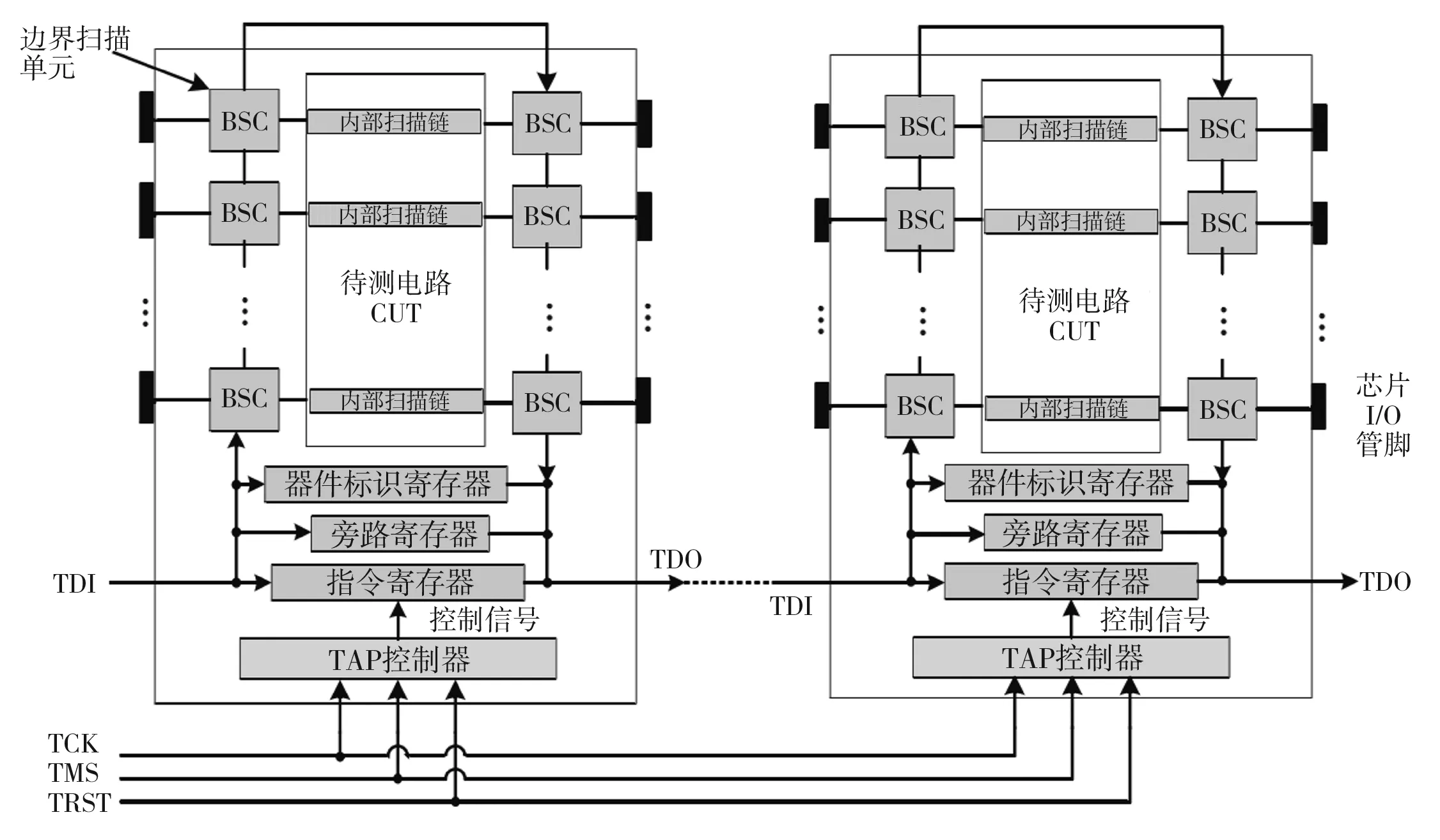
图1 边界扫描测试基本结构[9]

3 线性反馈移位寄存器的设计

3.1 内建自测试技术

关于线性反馈移位寄存器的设计与仿真所用的主要测试方法就是内建自测试的测试方法。内建自测试方法是可测性设计中的非常实用且好用的一种方法。内建自测试(BIST)就是在电路导入一个特殊的设计好的结构，在电路里测试生成、施加、分析和测试电路。以上的一系列操作都可以在电路本身内部完成，相对而言内建自测试是一种比较自动的测试方式。测试不仅要节约成本，还要节约测试的时间。这种测试方式在电路中导入一个结构，其实并不是一种损耗和浪费，而是既节省了人力又节省了时间，可谓是低成本、高效率的一种测试方法。在测试序列生成的过程中，有很多种测试方法，比如下文所提及到的伪随机测试。伪随机测试是通过线性反馈移位寄存器LFSR来实现的。(BIST)内建自测试的测试方法按照并发和非并发的方向可分为两类：一类是在线BIST，另一类是离线BIST。在线测试指的是测试与电路的正常操作同时进行。在线测试有一定的优点，这种测试方法常用在电路空闲时，在故障测试诊断过程中可以随时中断，电路的正常功能也可以重新正常开始，不影响电路的正常使用，随测随停。鉴于这一特性，这种在线BIST测试的方式常用在编码和比较电路中。离线BIST指的是使电路退出原来的工作状态，保持离线，再对电路进行测试。与在线BIST不同，离线BIST涉及的是基于被测电路结构描述的测试，通常测试的生成都以线性反馈移位寄存器的形式表现出来。它不在电路的正常功能条件下进行，但可以采用在系统级、板级和芯片级测试，也可以在制造现场进行操作级测试，这种测试方式不能测试实时故障[10]。BIST基本结构如图2所示。

图2 BIST结构

总体来说，内建自测试正如它的名字一样在电路内部，通过运用合理的可测试性设计的方式，使得待测电路具有自测试能力，完成电路自测的过程。这种测试方式极为方便，只需要对可控结构的设计与导入，便可以得出测试所需的结果，整个过程都是电路在自行完成，为测试节约了大量的时间[11]。

3.2 伪随机序列

如果一个序列，一方面它是可以预先确定的，一方面它又具有某种随机序列的随机特性，我们便称这种序列为伪随机序列。

3.2.1 同余伪随机序列

生成伪随机序列通常采用两种方法，第一种方法采用复现关系：

Xk=AXk-1+B(模为M) (k=1,2,3…)

(公式1)

这里X0>0，A>0，B≥0，M>X0，M>A，M>B。如果选择合适值，使得M=rm，则可写为：

Xk=AXk-1+B(模为rm) (k=1,2,3…)

(公式2)

3.2.2 M序列

一个n级线性反馈移存器的输出序列具有周期性，周期p≤2n-1。对于任意一个m阶的线性反馈移位寄存器，根据本原多项式C0X0+C1X1+C2X2+…+CiXi的系数Ci(i=1,2,3，…，m)，连接异或门反馈所形成的伪随机序列发生电路，均可生成最大长度为(2m-1)的序列，称之为M序列[12]。对于一个多项式φ(x) (n方)，只有满足下述条件方可产生M序列：

(1)φ(x)不可再进行因式分解;

(2)φ(x)可整除xq-1,q=2n-1;

(3)φ(x)除不尽xp-1,p>q。

3.3 仿真结果及验证

LFSR多用于提供伪随机数(pseudo-random)、伪噪声(pseudo-noise)、快速数字计数(fast digital oounters)、灰数(whitening)等一系列似是随机的二进制序列，实质上它具有一定的规则且与初始状态(又称种子)和反馈函数密切相关，掌握这一规律就可以根据前一个状态值来推算出后期的序列值。

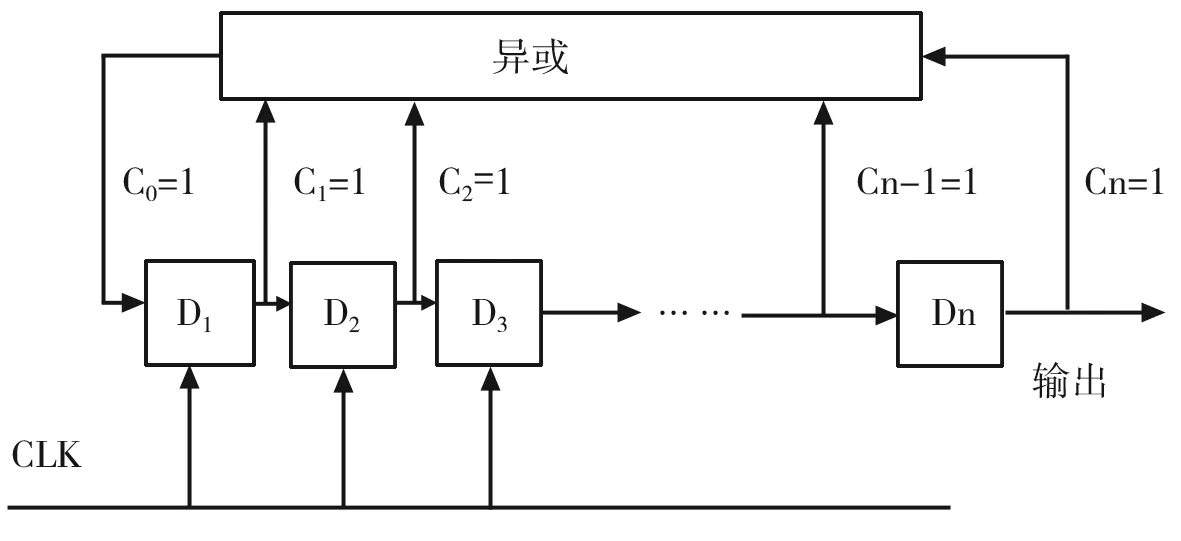
图3 EE型LFSR

本文研究内容就是基于5阶原多项式设计的LFSR线性反馈移位寄存器发生器，根据多项式1+x2+x5和1+x2+x3+x5+x16写出的Verilog语言程序。

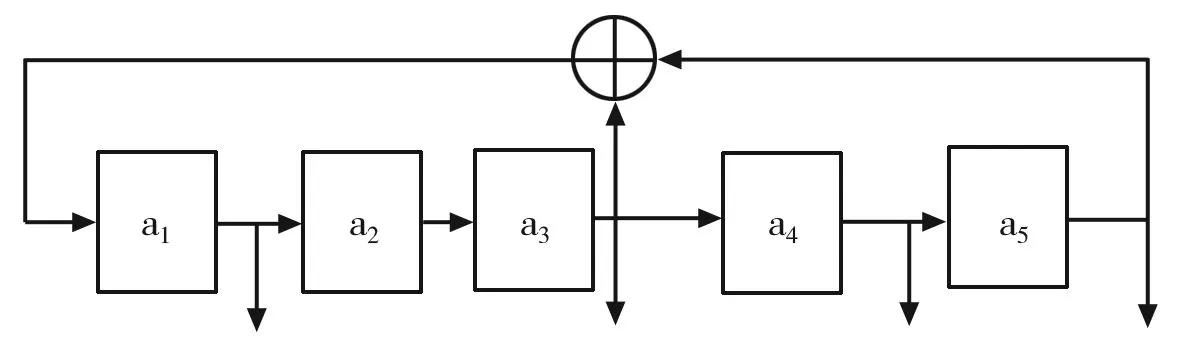
图4 五阶外接型LFSR结构图

为了使得所设计的LFSR能够正常工作，需要通过控制端的操作，对齐进行种子向量的初始化，在LFSR的Verilog代码设计中就是对线性反馈移位寄存器进行RST的赋值。

由程序可知，此本原多项式可写为1+x2+x5，由图5、图6可以看出，周期为310ns，周期为(25-1)×10ns。鉴于篇幅有限，仿真数据量较大，本文只对关键时间节点的仿真结果进行截图。可以得出基于本原多项式的线性反馈移位寄存器结构，验证其可以生成M序列。由图5可知在5ns的时刻，LFSR被初始化，种子向量为10000，然后依次按所设计的结构生成测试序列；在405ns，时钟的上升沿再次出现向量10000。由以上仿真数据可见，测试向量出现了周期性。

图5 5阶EE型LFSR仿真结果

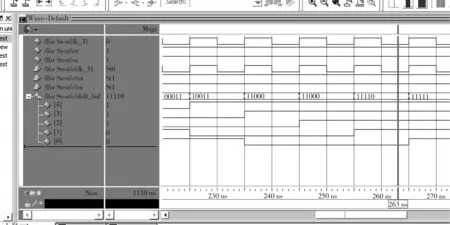
图6 5阶EE型LFSR仿真结果

4 结语

通过本文的设计，我们了解可测性设计的发展与前景，也深刻认识了BIST测试的重要性，并掌握线性反馈移位寄存器的数学模型。通过用Verilog语言设计5阶LFSR并利用ModelSim软件进行仿真，设计基于本原多项式的线性反馈移位寄存器结构，验证其可以生成M序列，可生成伪随机序列的寄存器与可生成M序列的硬件结构相同。验证了本原多项式及其互补多项式均可生成M序列，通过仿真结果验证EE型结构并没有影响M序列的生成。也用基于非本原多项式的LFSR结构验证了非本原多项式<2n-1,并非M序列。