基于非凸低秩约束的图像修复方法

孙艳敏，郭 强，张彩明

基于非凸低秩约束的图像修复方法

孙艳敏1,2，郭 强1,2，张彩明2,3

(1. 山东财经大学计算机科学与技术学院，山东 济南 250014；2.山东省数字媒体技术重点实验室，山东 济南 250014；3. 山东大学软件学院，山东 济南 250101)

受传输干扰或存储不当等因素的影响，现实应用中获取的某些图像通常会存在像素缺失现象，这给图像的后续分析与处理带来了一定影响。解决该问题的常用方法是对图像进行低秩修复。利用低秩特性进行修复的方法大多以秩函数建模，由于矩阵秩函数是非凸离散的，该模型的求解是一个NP难问题，所以通常利用核范数对矩阵的秩进行凸松弛。但是，基于核范数的修复方法与基于秩函数极小化的方法之间存在一定偏差，因此提出非凸低秩约束的图像修复方法。即采用log函数代替核范数对秩进行约束，能够克服核范数无法很好逼近秩最小化的问题。此外，为有效求解上述非凸模型，将目标函数转化为增广拉格朗日函数，利用交替方向乘子法求解图像修复模型。实验结果表明，该修复方法能够处理不同情况下的像素缺失问题，且修复性能明显好于现有低秩修复方法。

图像修复；核范数；交替方向乘子法；非凸低秩约束；增广拉格朗日函数

图像修复是图像处理和计算机视觉领域研究的热点问题[1]，其目标是根据图像中的已知区域提取可用图像信息来恢复破损区域或去除图像中的多余物体，以便获得符合人眼视觉要求或接近真实图像[2]。该技术在物体移除、影视特效以及艺术作品修复等领域具有广泛的应用。

图像修复方法通常是在修复过程中引入关于图像内在的结构信息和先验属性，利用数学理论建立先验模型，并依据先验模型求解缺失区域的像素。常用的修复算法大致可分为4类：基于偏微分方程(partial differential equations，PDE)的修复算法[3-5]、基于样本块的修复算法[6]、基于稀疏表示的修复算法[7]以及基于深度学习的修复算法[8-9]。基于偏微分的修复算法的主要思想是利用物理学中的扩散方程将待修复区域周围的信息传播到修复区域中，从而达到修复的目的。该方法主要适用于修复包含小尺度破损区域的图像如划痕和文字等，但当修复的面积较大时，修复效果会明显变差。其代表性算法包括TV算法[3]，BSCB算法[4]和CDD算法[5]等。为了弥补PDE修复算法的不足，基于样本块的修复算法应运而生。其实现修复的原理是在待修复图像的已知像素区域内按照某种规则搜索一个或多个图像块，将得到的图像块作为待修复块的估计进行填补，如此往复直到待修复区域填充完毕。这种方法虽然在较大区域的修复上较前者效果更好，但当图像本身的纹理特征不规则时，修复效果会明显下降。不同于以上2种方法，基于稀疏表示的修复算法则假定图像待修复区域和完好无损区域具备相同稀疏特性，对完好区域进行稀疏表示获得表示系数，再通过重构算法对图像破损区域进行重构，进而恢复成完整的图像。在修复过程中这类算法不仅能够改善图像修复质量，而且能够使修补的图像更加清晰。此外，深度学习近来也被应用到图像修复中。借助于深度学习较强的特征学习能力，在海量图像数据的支撑下，通过学习可对一些大尺度破损的图像进行较好的修复。但其存在训练时间长，且对计算机的硬件配置要求较高，网络模型缺乏理论解释等问题。

随着稀疏表示理论的发展，低秩表示成为近年来学术界研究的热点[10-11]。其是稀疏表示在矩阵上的扩展[12]，能够利用矩阵内样本点之间的内在关系[13-15]获得数据的全局性特征。受到低秩表示在挖掘数据全局信息方面具有很大优势的启发，以及图像本身具有的近似低秩特性[16-18]，本文假设原始图像可以由一个低秩矩阵表示[19]。基于该假设，图像修复的过程可以转换为一个低秩矩阵填充问题。

低秩矩阵填充可采用矩阵双线性因子分解[20-24]和矩阵秩最小化[25-29]2种策略进行。假设破损的矩阵为∈×n，为已知元素的位置构成的集合。基于双线性因子分解的填充算法通过求解以下模型可对缺失元素进行估计，即

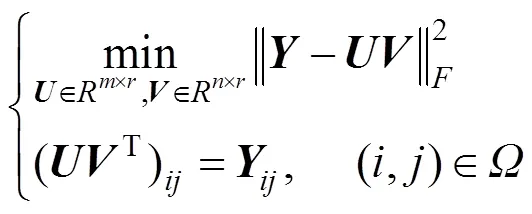
其中，为矩阵的秩。该方法将目标矩阵分解为2个低秩矩阵的乘积形式，求解过程中可避免复杂的矩阵奇异值分解，从而使得算法具有较低的计算复杂度。但是其必须预先估计矩阵的秩，这在一定程度上限制了该方法的可用性。

与基于双线性因子分解算法不同的是，基于秩最小化的填充算法通过式(2)得到矩阵的近似低秩估计

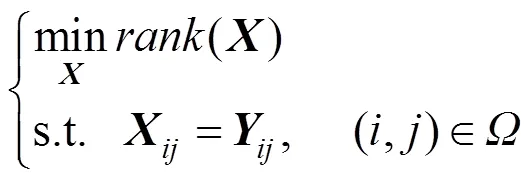
其中，()为矩阵的秩，即非零奇异值的个数。该方法无需知道矩阵的具体结构信息。因为当矩阵满足强不相干性且符合随机一致采样时，通过极小化矩阵的秩，能够以大概率对矩阵进行复原[25]。但是由于秩函数()的离散特性，矩阵的秩极小化是一个NP-hard问题。通常用求解核范数最小化(nuclear norm minimization，NNM)问题的方法来对其进行凸松弛[14,23,30]，进而式(2)可以转化为

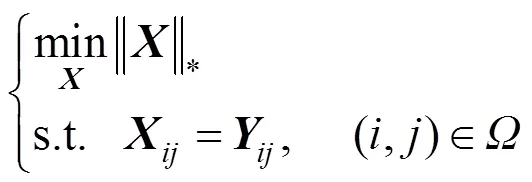
其中，||||*表示矩阵的核范数，即矩阵的所有奇异值之和。为了求解该模型，文献[31]提出了一种奇异值阈值方法(singular value thresholding，SVT)。但是该方法在求解NNM问题时，忽略了奇异值的物理意义而同等地收缩处理所有奇异值，导致在求解NNM问题时通常得到的是对原始秩最小化问题的次优解。事实上大的奇异值通常对应于数据的主要信息，应该被较小地收缩来保持数据的主要内容。文献[32]中的加权核范数极小化法(weighted nuclear norm minimization，WNNM)则根据奇异值的物理意义，通过赋予奇异值不同的权重来提高矩阵填充精度，但需要根据经验手动确定权重，使得该方法不能精确近似矩阵的秩函数。为了避免耗时的迭代收缩，文献[33]提出了一种利用低秩近似(low rank approximation，LRA)和截断奇异值的简单图像修复方法。此外，文献[34]认为基于矩阵NNM方法在求解过程中往往会更多地关注较大的奇异值，忽略较小的奇异值，这将导致所得到的矩阵虽然具有低秩性但却不能很好地逼近真实解。因此，上文提出了基于截断式矩阵核范数正则化(TNNR)的矩阵填充算法，其仅惩罚最小的-个奇异值(其中是矩阵的秩)。虽然TNNR在数据集上取得了很好的效果，但其在建立模型的过程中需要对矩阵的秩进行预估计，这一过程在真实场景中难以实现。

尽管核范数能够较好地逼近非凸的秩函数，且文献[25]给出了一定的理论保证，但其与秩函数的最佳逼近函数仍有一定差距，这使得在实际应用中其所获结果往往不是最优的。其原因为矩阵的每一个非零奇异值对秩函数来说是同等重要的，而核范数定义为全部非零奇异值之和，并且同时最小化，这样就使得每一个奇异值具有了不相同的贡献。为了克服上述问题，本文提出了一种非凸矩阵填充算法来进行图像修复。与基于核范数的模型相比，其能够更好地逼近原始的秩极小化问题，这是因为非凸松弛可以对不同奇异值进行不平衡惩罚，从而有利于对数据中主要信息的度量和刻画。此外，为了求得算法的一个最优解，本文采用了交替方向乘子法来求解该模型。

1 相关工作

为了更精准地逼近秩函数，学者们提出引入一些更加紧致的非凸函数来松弛秩函数。文献[26]采用Schatten-p(0<≤1)范数来作为秩函数的逼近函数，将低秩矩阵填充问题建模为

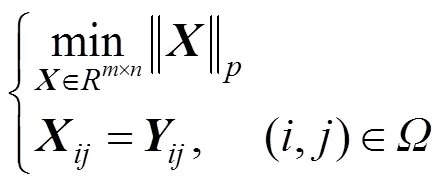
其中

当参数=1时，Schatten-p范数等价于核范数，即核范数是Schatten-p范数的一个特例。当越趋近于0时，Schatten-p范数对秩函数的逼近能力越强。该模型可以采用拉格朗日乘子法进行求解。数值实验结果表明，采用Schatten-p范数比采用核范数进行矩阵填充获得的效果更好。

文献[35]则用高斯函数

来逼近秩函数，其中，s为变量；为参数。将低秩矩阵填充问题建模为

该模型可充分利用高斯函数可微的性质，采用梯度投影算法进行求解。受高斯函数的启发，文献[36]则利用光滑双曲正切函数

建立光滑非凸优化模型，同样可采用梯度投影算法进行求解。对低秩矩阵填充问题和图像修复问题的实验结果表明，该算法取得了更好的结果。此外，也可采用非凸光滑的logdet(+T)函数作为秩函数()的包络来对矩阵填充问题建模[37]，该模型求解可以采用交替方向乘子法。

不同于上述非凸矩阵填充模型的图像修复方法，本文基于log函数的放缩性和泰勒展开函数的逼近性导出了一种简单有效的方法。

2 本文方法

2.1 动机分析

本文采用log函数近似秩函数主要从以下2个方面考虑：

(1) 从物理意义上讲，图像中较大的奇异值与图像的主要成分相关，因此较大奇异值需要被较小地约束以保留主要成分。但是矩阵核范数却将具有不同重要性的奇异值同等对待，这导致基于矩阵核范数的修复方法不能很好地保留图像主要成分。直观上的做法是，不同的奇异值应该根据重要性被不同程度地约束。一种策略是用加权核范数的形式，但是这种形式会引入更多的权重参数且需要手动确定权重，这使得加权核范数不能更精确近似秩函数。而本文采用奇异值的对数来保证较大奇异值的重要性，其在求解时对奇异值的收缩值仅与各个奇异值相关，这是更加合理的。

(2) 从数学意义上讲，由于秩函数是奇异值的0范数，是非凸不连续的函数，而核范数是奇异值的1范数，其最小化容易导致过惩罚的问题。于是，出现了许多利用非凸连续函数来逼近0范数的方法，例如：l范数[38-39](0<<1)、平滑截断绝对值偏差[40]、MCP函数[41]以及指数型罚函数[42]等。这些非凸近似函数较1范数具有更好的性能，且更适合用于图像修复。

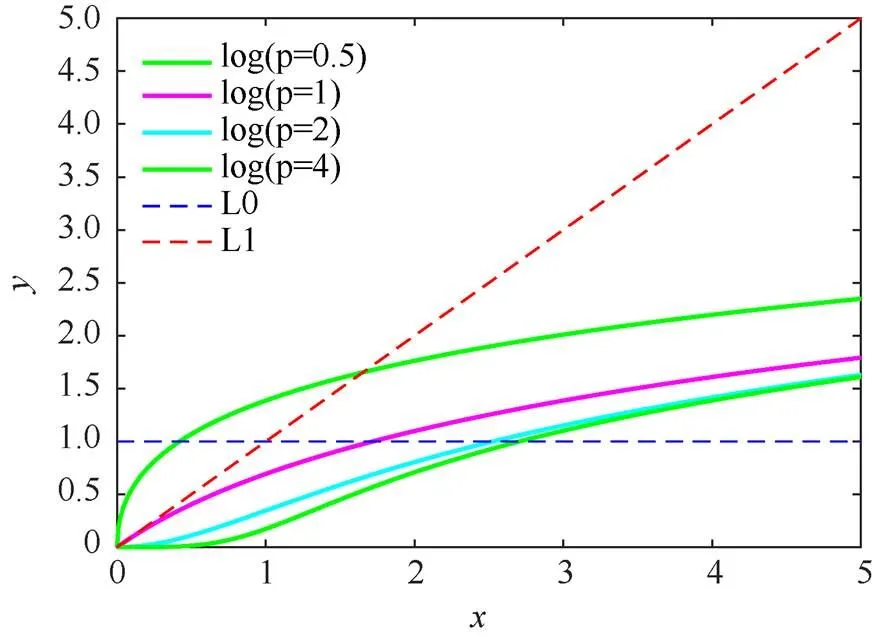
图1 l1范数和函数对l0范数逼近程度比较

2.2 基于log函数的修复模型

通过以上分析，理论上可采用以下非凸低秩的正则化模型对图像进行修复

其中

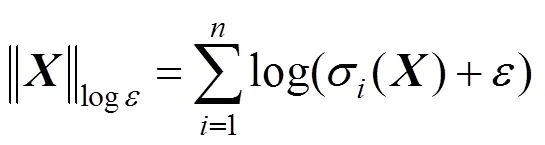
>1为常数；()为矩阵的第个奇异值。考虑到自然图像会受到噪声干扰，需引入噪声正则项以增加模型鲁棒性，即

其中，为正则化参数；为数据的噪声矩阵。

2.3 模型的优化求解过程

由于||||log的非凸性，式(11)难以直接求解，因此本文利用一阶泰勒展开式[43]来线性逼近式||||log，将其代入泰勒展开式()=(0)+ʹ(0) (-0)，得

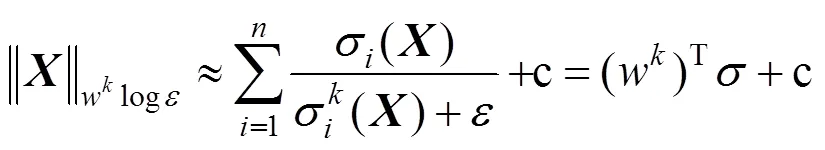
通过引入辅助变量=及拉格朗日乘子矩阵和，将式(11)转换为有关增广拉格朗日函数的无约束最小化模型，即

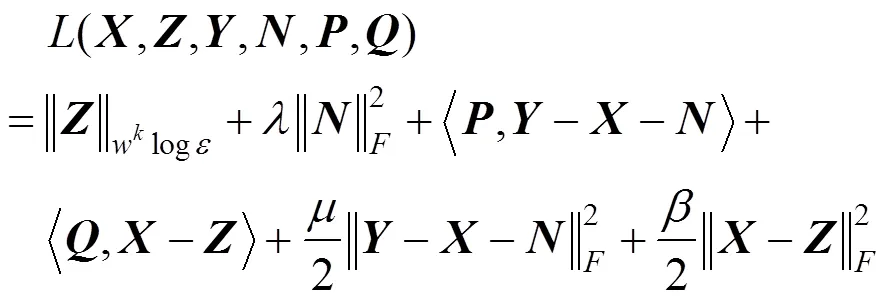
其中，和为正的惩罚权重参数。此外，为了方便起见，记

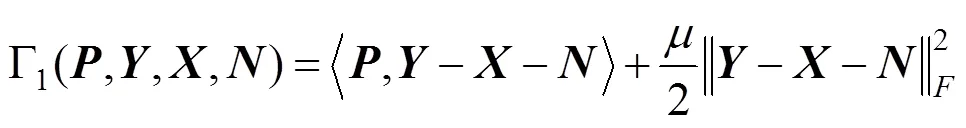
由于式(13)中的变量是可分离的，所以利用交替最小化方法[44]来求解。具体地，在一次迭代中，首先固定，，，，，并利用式(15)更新，得

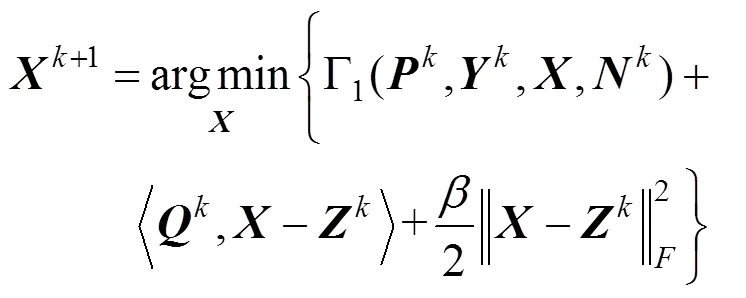
由于式(15)的目标函数是可微的，因此+1有如下闭式解

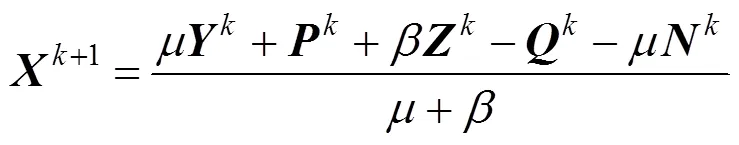
然后，固定，，，，，利用下式更新，得

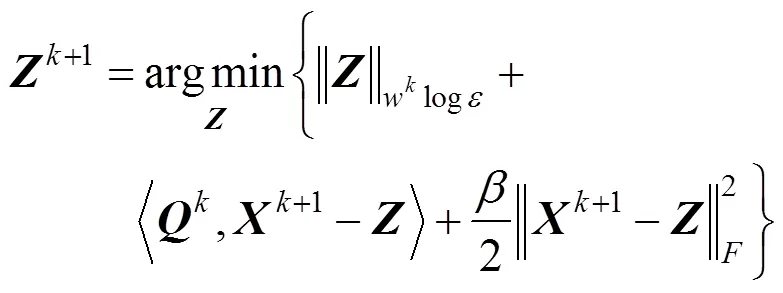
根据文献[43]引理1，可得

类似地，固定，，，，，利用式(19)更新，则有

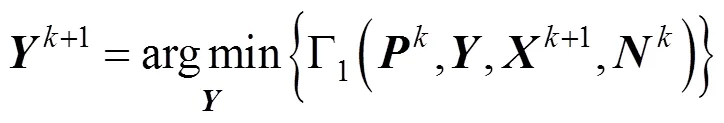
由于式(19)中的目标函数是可微的，故通过使其一阶导数等于零可得

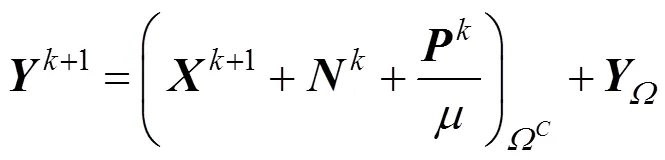
其中，是指标集的补集。

其次，固定，，，，，利用式(20)更新，有

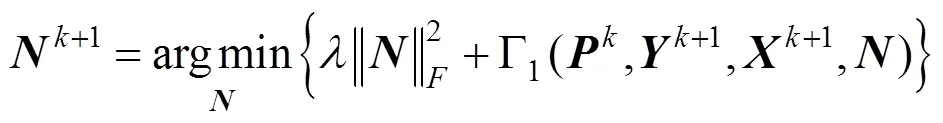
由于式(21)的目标函数是可微的，易得+1的解为

最后，固定，，，，利用下式更新增广拉格朗日乘子，为

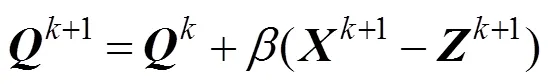
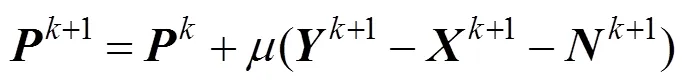
根据上述的求解过程，可得本文算法：

输入：破损图像Y，指标集W。初始化：X=0，N=0，Z=0，P=0，Q=0和m=b=1e-8，k=100。输出：修复图像X。步骤1. 通过式(15)更新Xk+1。步骤2. 通过式(17)更新Zk+1。步骤3. 通过式(19)更新Yk+1。步骤4. 通过式(21)更新Nk+1。步骤5. 通过式(23)更新pk+1。步骤6. 通过式(24)更新Qk+1。步骤7. 通过m=tm，b=tb更新乘数m和b。步骤8. 重复执行步骤1～7，直到满足收敛条件：。步骤9. 结束。

需要说明的是，为避免迭代收敛过程过于缓慢，本文通过利用文献[45]的方法来加速收敛过程，即每一次迭代中的和分别是上一次迭代的倍，即=，=，其中Î[1.1, 1.2]。

3 实验结果与分析

通过将本文方法与WNNM-MC[32]，TCTR[45]，MC-NC[46]，LRMC[47]和LRTC-TNN[47]5种方法进行比较分析，以验证本文方法的有效性。实验所用计算机配置为：Intel Core i7-6700 CPU @3.40 GHz，8 GB内存，软件平台为MATLAB R2018a。

参数设置下：=0.01max(((T)))，=1。其他5种修复算法的实现代码均从作者主页上获取，相关参数采用默认值。对修复后图像的质量从主观的视觉效果以及客观的量化指标2方面进行评价。本文采用峰值信噪比(peak signal-to-noise ratio，PSNR)和特征相似度均值(feature similarity index mersure，FSIM)这2种常用的定量标准来量化修复后图像的质量。原始测试图像如图2所示。

①②③ ④⑤⑥ ⑦⑧⑨

3.1 随机丢失像素修复性能比较

3.1.1 无噪声数据的实验结果

表1为在不同像素缺失率(=0.1, 0.3, 0.5)下，采用不同方法所得修复图像的PSNR和FSIM值。从中可以看出，本文方法的量化性能明显优于WNNM-MC和MC-NC，略好于LRMC，LRTC-TNN和TCTR。本文方法的平均PSNR值分别比WNNM-MC，MC-NC，LRMC，LRTC-TNN和TCTR高出2.56 dB，3.17 dB，1.17 dB，0.14 dB和0.12 dB。

为比较不同方法修复图像的视觉效果，图3为在像素缺失率(=0.5)的情况下，各种修复方法对图2中不同测试图像的修复结果。可以看出，采用TCTR方法修复后的图像含有非常明显的瑕疵点，尤其是图像的边缘部分，未能将图像边缘信息有效地恢复，而本文方法的视觉效果则明显好于TCTR。产生上述问题的原因在于，TCTR每次对固定秩为的矩阵执行SVD。虽然该算法可以缩短运行时间，但其忽略了现实图像的秩是一变量的事实。

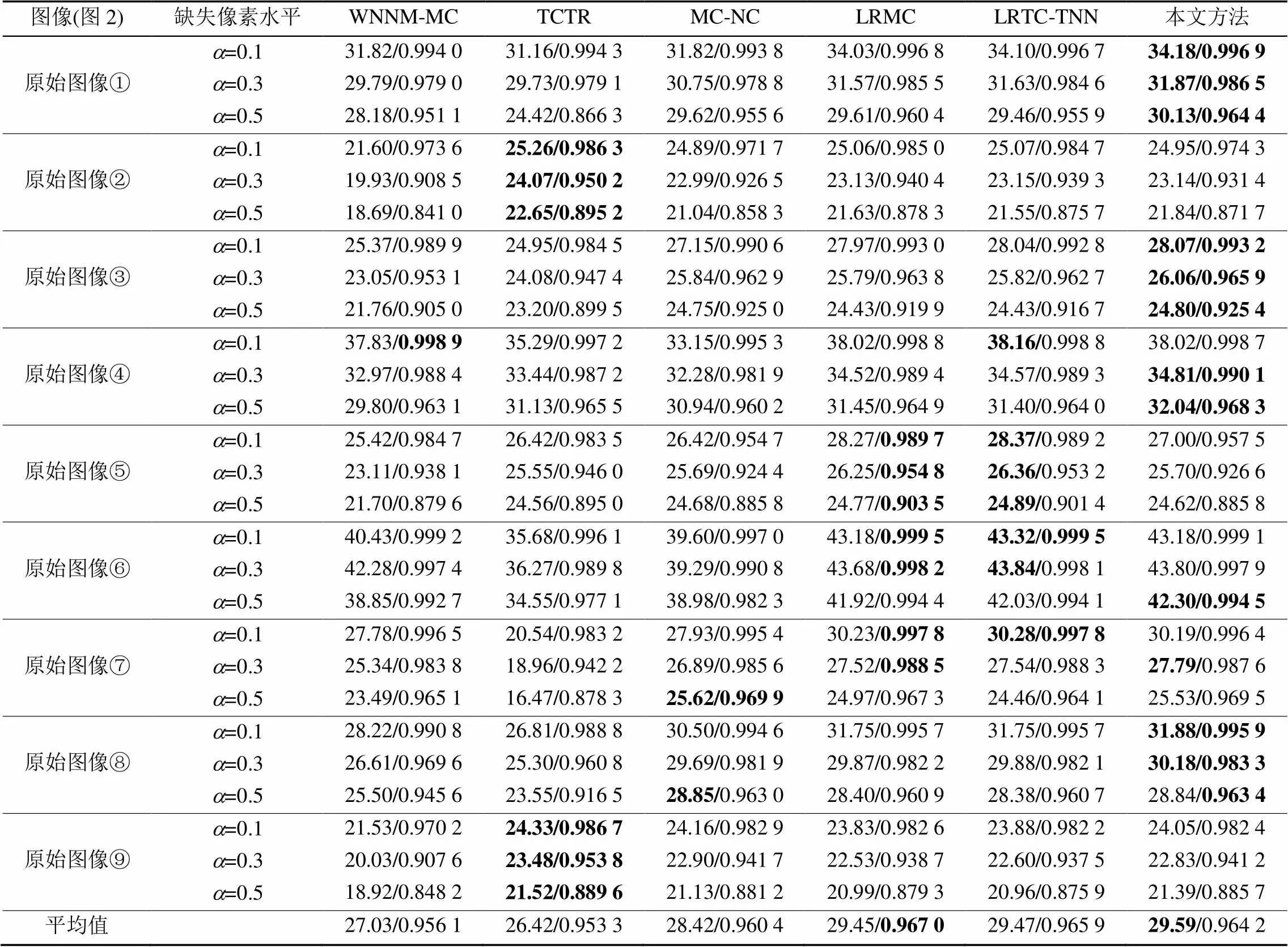
表1 不同方法修复结果PSNR/FSIM比较(无噪声)

图3 不同算法对缺失率a=0.5的图像修复效果图

3.1.2 含噪声数据的实验结果

表2为在不同噪声水平(=5,10,15)下，采用不同方法所得修复图像的PSNR和FSIM值。从表2可以发现，噪声降低了所有方法的性能，而且在大多数情况下，基于非凸松弛的方法可获得较好的结果。

表2 不同方法修复结果PSNR/FSIM比较(有噪声)

为进一步比较修复图像的视觉效果，图4为在=0.5，=15情况下，不同修复方法对测试图像的修复结果。由于实验使用的图片分辨率较低，因此无法较好地观察到复原区域与原始图片对应区域之间的细节差异，于是图5给出了不同修复方法对测试图像的局部细节修复结果。不难看出，采用LRMC修复后的图像整体过于模糊。如图5(f)的第3行图像所示，图像细节特征丢失严重。产生上述问题的原因在于，基于NNM模型的算法忽略了奇异值的物理意义而同等地收缩所有奇异值。此外采用WNNM算法进行图像修复虽然效果较好，但需要引入额外的权重参数。而本文利用奇异值的对数来保证较大奇异值的重要性，并在求解时要求奇异值的收缩值仅与各个奇异值相关，没有引入额外的权重参数，这是更加合理的收缩算法。

3.2 像素块丢失修复性能比较

3.2.1 无噪声数据的实验结果

本文随机选取图像的某一个30×30的方形区域作为缺失区域，将其数量定义为，并将处理后得到的图像作为破损图像来验证本文算法的有效性。各方法的FSIM和PSNR见表3，以及相应的视觉效果如图6所示。根据表中相应的PSNR和FSIM值可以看出，MC-NC在PSNR平均值方面优于本文算法0.13 dB，而在FSIM平均值方面则两者相同，说明从客观的量化指标进行评价，本文方法与MC-NC相当。

图4 不同算法对缺失率a=0.5，噪声水平t=15的图像修复效果图

图5 不同算法对缺失率a=0.5，噪声水平t=15的图像修复细节效果图

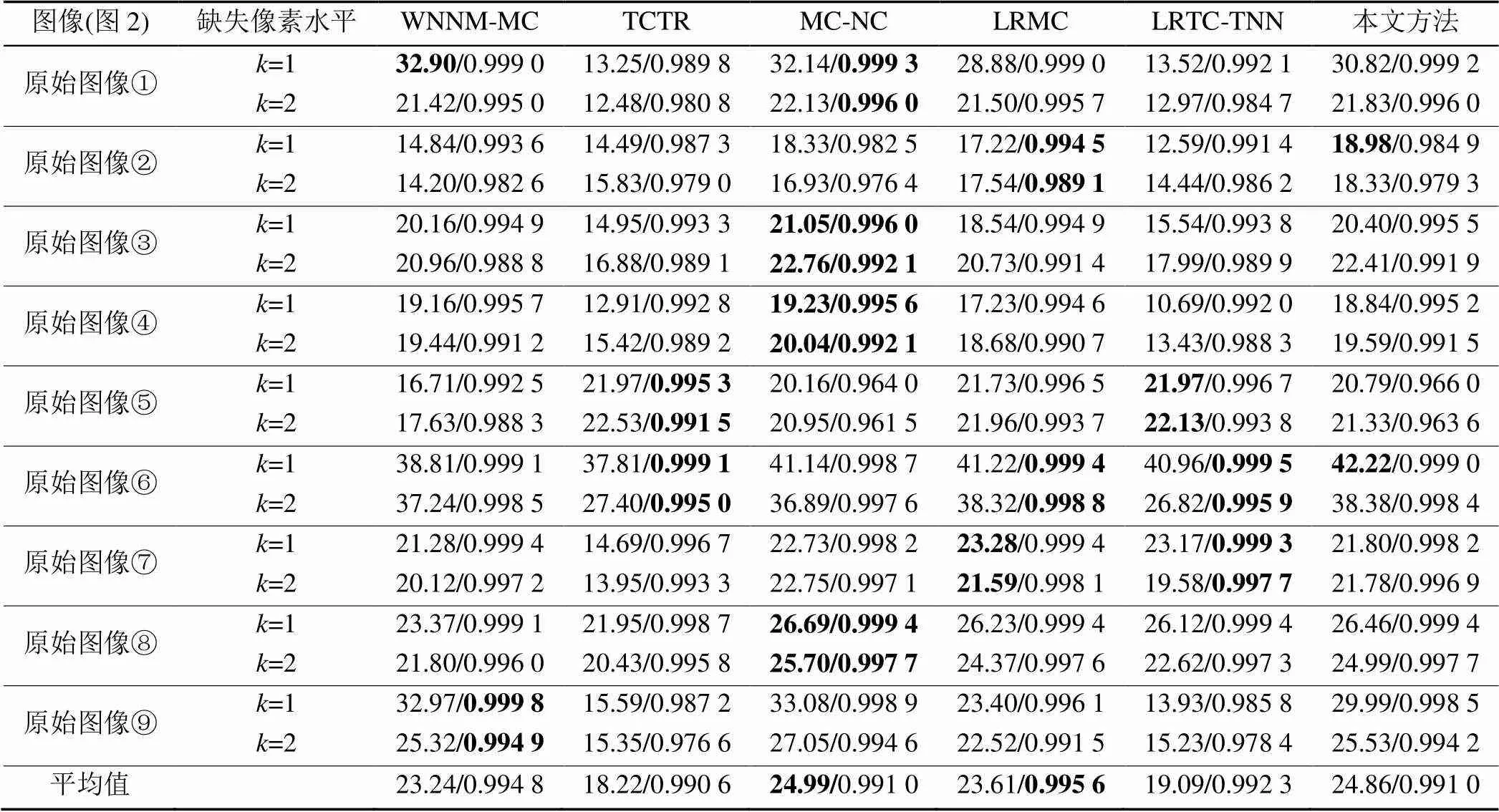
表3 不同方法修复结果PSNR/FSIM比较(无噪声，30×30)

图6 不同算法对缺失率k=2的图像修复效果图

从图6主观视觉效果方面而言，本文方法所获得的修复结果不仅与MC-NC相当，并且明显优于其他相关方法，尤其是对于含有大量冗余信息的图像，本文方法的修复效果较好。需要说明的是，如图6(c)所示，尽管MC-NC方法可以获得最佳的视觉效果，但在实际运行中需要进行耗时的逐行更新。此外，TCTR不适合修复随机丢失像素以及丢失较大区域的图像，从定量标准和视觉效果两方面来说，TCTR的修复性能最差。

3.2.2 含噪声数据的实验结果

表4为固定=2时，在不同噪声水平(=5,10,15)下，不同算法取得的PSNR和FSIM值。可以看出，平均MC-NC取得了最高的PSNR值，而本文算法取得了最高的FSIM值。总体而言，本文算法具有相对较好的修复果。

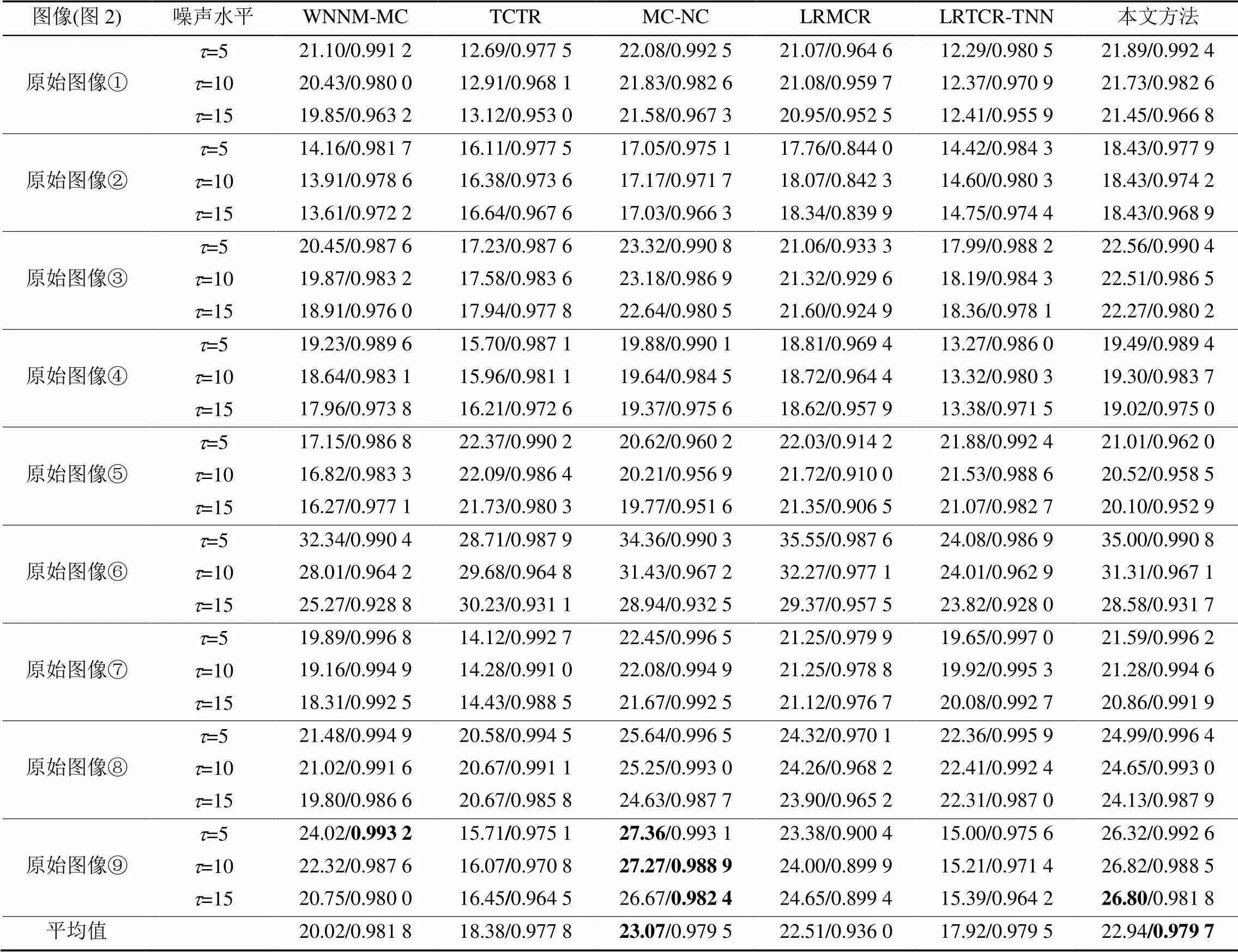
表4 不同方法修复结果PSNR/FSIM比较(有噪声，30×30，k=2)

图7为在=2，=10的情况下，各种修复方法对不同测试图像的修复结果，为进一步从视觉上观察到补全区域与原始图片对应区域之间的细节差异，图8给出了图像的局部细节修复结果。从图8中不难看出，本文方法和MC-NC的视觉效果要远好于TCTR，LRMC和LRTC-TNN，略好于WNNM-MC。WNNM-MC尽管具有较高的量化指标，但其结果存在一定程度的模糊，如图8(e)所示。此外，从图8(g)中可以发现，LRTC-TNN无法有效地修复缺失的像素块，这是由于其对参数较为敏感。

综上所述，本文方法不仅具有较高的PSNR和FSIM，以及较强的鲁棒性，而且其修复的图像具有很好的视觉效果，能够有效地保持图像细节。

4 结 论

本文提出了一种基于非凸正则化项的矩阵填充模型，并结合交替方向乘子法对其进行求解，实验结果表明，在不同缺失率下以及不同噪声影响下，本文算法均能获得较好的修复效果。由于迭代过程中涉及到矩阵的奇异值分解，使得算法的计算复杂度较高，如何提高算法的计算效率是下一步研究工作的主要内容。

图7 不同算法对缺失率k=2，噪声水平t=10的图像修复效果图

图8 不同算法对缺失率k=2，噪声水平t=10的图像修复细节效果图

[1] GUILLEMOT C, LE M O. Image inpainting: overview and recent advances[J]. IEEE Signal Processing Magazine, 2014, 31(1): 127-144.

[2] 冯象初, 王斯琪, 李小平. 图像修复问题的低秩对偶逼近算法[J]. 西安电子科技大学学报, 2016, 43(4): 172-177.

FENG X C, WANG S Q, LI X P. Low-rank and dual approximation method for image inpainting problems[J]. Journal of Xidian University, 2016, 43(4): 172-177 (in Chinese).

[3] 张桂梅, 李艳兵. 结合纹理结构的分数阶TV模型的图像修复[J]. 中国图象图形学报, 2019, 24(5): 700-713.

ZHANG G M, LI Y B. Image inpainting of fractional TV model combined with texture structure[J]. Journal of Image and Graphics, 2019, 24(5): 700-713 (in Chinese).

[4] 尹芳, 陈田田. 均场退火算法在单幅灰度图像高光检测与恢复中的应用[J]. 计算机辅助设计与图形学学报, 2017, 29(5): 829-837.

YI F, CHEN T T. Application of mean field annealing in specular detection and recovery for a grayscale image[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(5): 829-837 (in Chinese).

[5] 窦立云, 徐丹, 李杰, 等. 基于双树复小波的图像修复[J]. 计算机科学, 2017, 44(S1): 179-182, 191.

DOU L Y, XU D, LI J, et al. Image inpainting based on dual-tree complex wavelet transform[J]. Computer Science, 2017, 44(S1): 179-182, 191 (in Chinese).

[6] 陶兆胜, 张敬寒, 王磊, 等. 基于边缘特征和像素结构相似度的图像修复算法[J]. 计算机辅助设计与图形学学报, 2019, 31(10): 1768-1776.

TAO Z S, ZHANG J H, WANG L, et al. Image inpainting algorithm based on edge feature and pixel structure similarity[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(10): 1768-1776 (in Chinese).

[7] 高成英, 徐仙儿, 罗燕媚, 等. 基于稀疏表示的物体图像修复[J]. 计算机学报, 2019, 42(9): 1953-1965.

GAO C Y, XU X E, LUO Y M, et al. Object image inpainting based on sparse representation[J]. Chinese Journal of Computers, 2019, 42(9): 1953-1965 (in Chinese).

[8] LI J Y, WANG N, ZHANG L F, et al. Recurrent feature reasoning for image inpainting[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2020: 7760-7768.

[9] ZHAO L, MO Q H, LIN S H，et al. UCTGAN: diverse image inpainting based on unsupervised cross-space translation[C]// 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2020: 5741-5750.

[10] UDELL M, HORN C, ZADEH R B, et al. Generalized low rank models[J]. Foundations and Trends in Machine Learning, 2016, 9(1): 1-118.

[11] 郭强, 张彩明, 张云峰, 等. 基于最小方差估计的图像低秩去噪[J]. 计算机辅助设计与图形学学报, 2015, 27(12): 2237-2246.

GUO Q, ZHANG C M, ZHANG Y F, et al. Low-rank image denoising based on minimum variance estimator[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(12): 2237-2246 (in Chinese).

[12] CAI T T, ZHANG A. Sparse representation of a polytope and recovery of sparse signals and low-rank matrices[J]. IEEE Transactions on Information Theory, 2014, 60(1): 122-132.

[13] 张倩侃, 计忠平, 付晓峰. 二次联合稀疏表示和低秩近似的浅浮雕优化[J]. 中国图象图形学报, 2020, 25(6): 1245-1259.

ZHANG Q K, JI Z P, FU X F. Bas-relief optimization based on twice-joint sparse representation and low-rank approximation[J]. Journal of Image and Graphics, 2020, 25(6): 1245-1259 (in Chinese).

[14] LIU G C, LIN Z C, YAN S C, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184.

[15] LU X Q, WANG Y L, YUAN Y, et al. Graph-regularized low-rank representation for destriping of hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7): 4009-4018.

[16] 刘成士, 赵志刚, 李强, 等. 加强的低秩表示图像去噪算法[J]. 计算机工程与应用, 2020, 56(2): 216-225.

LIU C S, Z Z G, LI Q, et al. Enhanced low-rank representation image denoising algorithm[J]. Computer Engineering and Applications, 2020, 56(2): 216-225 (in Chinese).

[17] 白宏阳, 马军勇, 熊凯, 等. 图像修复中的加权矩阵补全模型设计[J]. 系统工程与电子技术, 2016, 38(7): 1703-1708.

BAI H Y, MA J Y, XIONG K, et al. Design of weighted matrix completion model in image inpainting[J]. Systems Engineering and Electronics, 2016, 38(7): 1703-1708 (in Chinese).

[18] HE W, ZHANG H Y, ZHANG L P, et al. Hyperspectral image denoising via noise-adjusted iterative low-rank matrix approximation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 3050-3061.

[19] JI H, LIU C Q, SHEN Z W, et al. Robust video denoising using low rank matrix completion[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York: IEEE Press, 2010: 1791-1798.

[20] WEN Z W, YIN W T, ZHANG Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over relaxation algorithm[J]. Mathematical Programming Computation, 2012, 4(4): 333-361.

[21] HE W, ZHANG H Y, ZHANG L P, et al. Total-Variation-Regularized low-rank matrix factorization for hyperspectral image restoration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 178-188.

[22] XU Y Y, YIN W T, WEN Z W, et al. An alternating direction algorithm for matrix completion with nonnegative factors[J]. Frontiers of Mathematics in China, 2012, 7(2): 365-384.

[23] ZHOU P , LU C Y, LIN Z C , et al. Tensor factorization for low-rank tensor completion[J]. IEEE Transactions on Image Process, 2018, 27(3): 1152-1163.

[24] SHANG F H, CHENG J, LIU Y Y, et al. Bilinear factor matrix norm minimization for robust PCA: Algorithms and applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(9): 2066-2080.

[25] CANDES E J, RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772.

[26] NIE F P, WANG H, HUANG H, et al. Joint schatten p-norm and lp-norm robust matrix completion for missing value recovery[J]. Knowledge and Information Systems, 2015, 42(3): 525-544.

[27] NIE F, HUANG H, DING C, et al. Low-rank matrix recovery via efficient schatten p-norm minimization[C]//The 26th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2012: 655-661.

[28] LU C Y, ZHU C B, XU C Y, et al. Generalized singular value thresholding[C]//The 29th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2015: 1805-1811.

[29] LARSSON V, OLSSON C. Convex low rank approximation[J]. International Journal of Computer Vision, 2016, 120(2): 194-214.

[30] DAI Y H, LI H D, HE M Y, et al. A simple prior-free method for non-rigid structure-from-motion factorization[J]. International Journal of Computer Vision, 2014, 107(2): 101-122.

[31] CAI J F, CANDÈS E J, SHEN Z W, et al. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982.

[32] GU S H, XIE Q, MENG D Y, et al. Weighted nuclear norm minimization and its applications to low level vision[J]. International Journal of Computer Vision, 2017, 121(2): 183-208.

[33] GUO Q, GAO S S, ZHANG X F, et al. Patch-based image inpainting via two-stage low rank approximation[J]. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(6): 2023-2036.

[34] LIU Q, LAI Z H, ZHOU Z W, et al. A truncated nuclear norm regularization method based on weighted residual error for matrix completion[J]. IEEE Transactions on Image Processing, 2015, 25(1): 316-330.

[35] GHASMEI H, MALEK M M, BABAIE Z M, et al. SRF: matrix completion based on smoothed rank function[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing. New York: IEEE Press, 2011: 3672-3675.

[36] GENG J, WANG L S, WANG Y F, et al. A non-convex algorithm framework based on DC programming and DCA for matrix completion[J]. Numerical Algorithms, 2015, 68(4): 903-921.

[37] KANG Z, PENG C, CHENG J, et al. LogDet rank minimization with application to subspace clustering[EB/OL]. [2020-09-11]. https://www.hindawi.com/journals/cin/2015/824289/.

[38] TAHERI O, VOROBYOV S A. Sparse channel estimation with lp-norm and reweighted l1-norm penalized least mean squares[C]//2011 IEEE International Conference on Acoustics, Speech, and Signal Processing. New York: IEEE Press, 2011:2864-2867.

[39] XU Z B, ZHANG H, WANG Y, et al. L1/2 regularization[J]. Science China (Information Sciences), 2010, 53(6): 1159-1169.

[40] FAN J, LI R. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of the American Statistical Association, 2001, 96(456): 1348-1360.

[41] CAO W F, WANG Y, YANG C, et al. Folded-concave penalization approaches to tensor completion[J]. Neurocomputing, 2015, 152(25): 261-273.

[42] GAO C X, WANG N Y, YU Q R, et al. A feasible nonconvex relaxation approach to feature selection[C]//The 25th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2011: 356-361.

[43] DONG W S, SHI G M, LI X, et al. Compressive sensing via nonlocal low-rank regularization[J]. IEEE Transactions on Image Processing, 2014, 23(8): 3618-3632.

[44] LU C Y, FENG J S, YAN S C, et al. A unified alternating direction method of multipliers by majorization minimization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 527-541.

[45] LU C Y, FENG J S, LIN Z C, et al. Exact low tubal rank tensor recovery from Gaussian measurements[C]//The 27th International Joint Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2018: 2504-2510.

[46] NIE F P, HU Z X, LI X L. Matrix completion based on non-convex low-rank approximation[J], IEEE Transactions on Image Processing, 2019, 28(5): 2378-2388.

[47] LU C. A library of ADMM for sparse and low-rank Optimization. National University of Singapore, June 2016[EB/OL]. [2020-10-15]. https://github.com/canyilu/ LibADMM-toolbox.

Image inpainting using non-convex and low-rank constraint

SUN Yan-min1,2, GUO Qiang1,2, ZHANG Cai-ming2,3

(1. School of Computer Science and Technology, Shandong University of Finance and Economics, JinanShandong 250014, China; 2. Shandong Key Laboratory of Digital Media Technology, JinanShandong 250014, China; 3. School of Software, Shandong UniversityJinanShandong 250101, China)

Due to transmission interference or improper storage, there exist some missing pixels in the images obtained in the real scene, which causes obstacles to the subsequent processing and analysis of the images. The key solution for missing pixels is to recover the image with low rank prior. However, since the rank function is discrete, the model that minimizes the rank is an NP-hard problem. In order to address this issue, a commonly used method is to employ an image-inpainting algorithm based on the nuclear norm. Unlike the methods based on the nuclear norm minimization, this paper proposed an image-inpainting algorithm using non-convex low-rank constraints, which replaced the traditional nuclear norm with a log function and overcame the inability of the nuclear norm to approach the rank minimization. In addition, to optimize the non-convex model, the augmented Lagrangian multiplier method was adopted to derive an alternating minimization algorithm. Experimental results demonstrate that the proposed method can deal with different missing pixel rates, and can far outperform other low-rank inpainting methods in inpainting.

image inpainting; nuclear norm; alternating direction method of multiplier; non-convex and low-rank constraints; augmented Lagrangian method

TP 391

10.11996/JG.j.2095-302X.2021030414

A

2095-302X(2021)03-0414-12

2020-12-02；

2020-12-26

2 December，2020；

26 December，2020

国家自然科学基金项目(61873145，U1609218)；山东省省属高校优秀青年人才联合基金(ZR2017JL029)

National Natural Science Foundation of China (61873145, U1609218);Supported by Youth Foundation of Shandong Province of China (ZR2017JL029)

孙艳敏(1993-)，女，山东济南人，硕士研究生。主要研究方向为数字图像修复。E-mail：1689980961@qq.com

SUN Yan-min (1993-), female, master student. Her main research interest covers digital image inpainting. E-mail：1689980961@qq.com

郭 强(1979–)，男，山东济南人，教授，博士。主要研究方向为图形图像处理、计算机视觉等。E-mail：guoqiang@sdufe.edu.cnE-mail：guoqiang@sdufe.edu.cn

GUO Qiang(1979-), male, professor, Ph.D. His main research interests cover graphic image processing, computer vision, etc.