倾转四旋翼飞行器直升机模式操稳特性分析

周攀, 陈仁良, 俞志明

(南京航空航天大学 航空学院 直升机旋翼动力学国家级重点实验室, 江苏 南京 210016)

倾转旋翼飞行器是直升机和固定翼飞机的结合体，具有垂直起降及高速巡航的能力，该特点使得倾转旋翼飞行器一直是研究的热门[1-3]。为了进一步提高垂直起降飞行器的载荷能力、巡航速度以及航程，贝尔直升机公司根据美国军方对于下一代重型旋翼机的要求，提出了一种倾转四旋翼(QTR)的概念方案[4]，该倾转旋翼机采用了与V-22相同的短舱系统并且设计负载与运输机C-130J相同。

近年来，国内外都已经开始了倾转四旋翼飞行器的研究，不过当前的技术研究尚处于探索试验阶段。国外的学者研究方向主要围绕着倾转四旋翼飞行器的气动性能展开[5-6]。国内学者主要在飞行力学建模，倾转过渡阶段的控制方法等方面展开[7-8]，然而针对直升机模式下操稳特性方面的研究还不完全。

在进行操稳特性分析之前，需确定飞行器的操纵策略。文献[9]根据倾转双旋翼飞行器在3种飞行模式下的操纵特性及配平分析结果，提出了一套适用于全模式的操纵策略，进而设计出了飞行控制器。文献[10]以姿态角变化及驾驶员负荷作为性能指标，利用最优控制方法，得到了倾转双旋翼飞行器在倾转过渡的过程中的最优操纵策略，计算结果与试飞数据吻合较好。文献[11]将纵向周期变距和升降舵偏转角用短舱倾转角来表示，解决了倾转双旋翼在纵向平面内的操纵冗余问题，并运用最优化方法对飞行器的不同模式进行了配平计算。倾转四旋翼飞行器具有比倾转双旋翼更加复杂的操纵冗余问题，尤其是在直升机模式下，其操纵舵面有12个，如何确定一种操纵策略是倾转四旋翼飞行器操纵冗余问题中必须解决的难题之一。

操稳特性是飞行器非常重要的飞行力学特性。文献[12]以XV-15为样机，针对其操纵机构的特点，深入研究了倾转旋翼机在不同飞行模式下的稳定性。文献[13]对XV-15建立了线性化的模型，并利用状态空间矩阵、Bode图和特征值对其稳定性和操纵性进行了分析，得到的结果与飞行试验数据进行了比较。文献[14]对某小型无人倾转旋翼机开展了全尺寸的吹风试验，研究了该飞行器的操纵特性，得到了总距、副翼及升降舵的操纵功效。文献[15]建立了带有吊挂的直升机模型并根据小扰动假设对其模型进行线化，分析了系统的稳定性导数矩阵。针对倾转四旋翼飞行器，由于其旋翼布局方式以及旋翼尾流对机翼的干扰，随着速度的变化，其操纵性和稳定性会发生明显改变。对操稳特性的深入研究有助于了解倾转四旋翼飞行器的飞行力学特性，能为后续控制系统的设计提供理论依据。

鉴于此，本文首先对倾转四旋翼飞行器的各部件进行了气动力建模，在考虑旋翼-机翼之间的干扰情况下，将模型的计算结果与试验结果进行了比较。由于飞行器在直升机模式下操纵面多，针对其操纵冗余问题，根据总距和周期变距的组合方式，提出了一种适用于直升机模式下的操纵策略。基于该操纵策略，对飞行器不同的速度状态进行了配平计算，分析了飞行器的配平特性。最后，对飞行器的操稳特性进行了分析，包括操纵功效、操纵耦合、稳定性导数及特征根这4个方面。

1 倾转四旋翼建模

本文的建模对象为自行研制的倾转四旋翼飞行器，其主要气动部件包括：旋翼系统、机翼、机身、垂尾等，布局如图1所示。前后机翼的两端安装有旋翼，且旋翼能随着短舱绕倾转轴实现倾转。4副旋翼中，对角旋翼的旋向相同，相邻旋翼的旋向相反。其中左前方旋翼为右旋旋翼，用数字1表示，其他旋翼依次用数字2，3，4表示。机翼采用襟副翼一体的设计，兼具飞机模式下副翼和升降舵的功效。垂尾安装有方向舵，提供飞机模式下的航向操纵。其总体参数如表1所示。

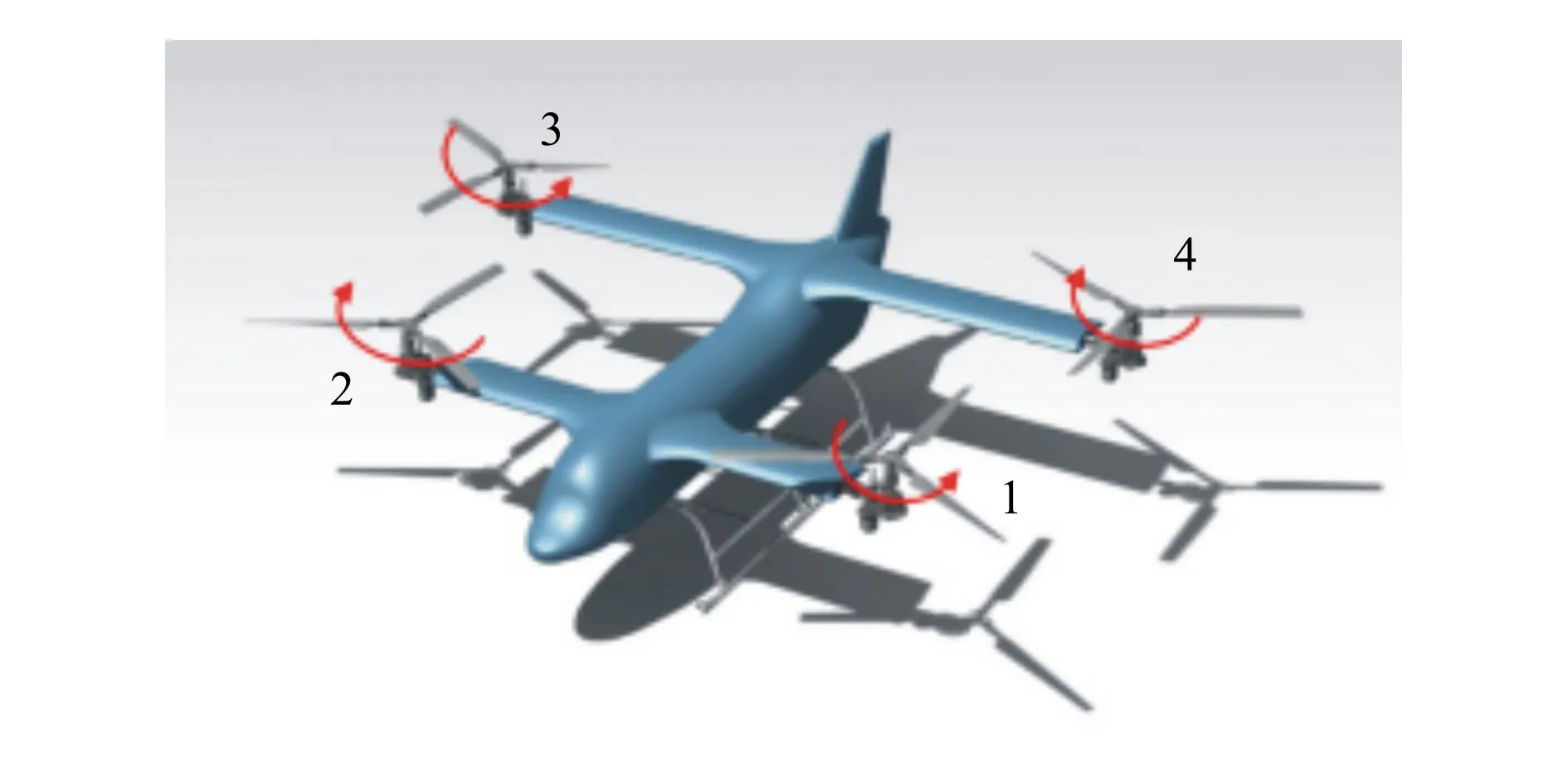
图1 倾转四旋翼飞行器布局图

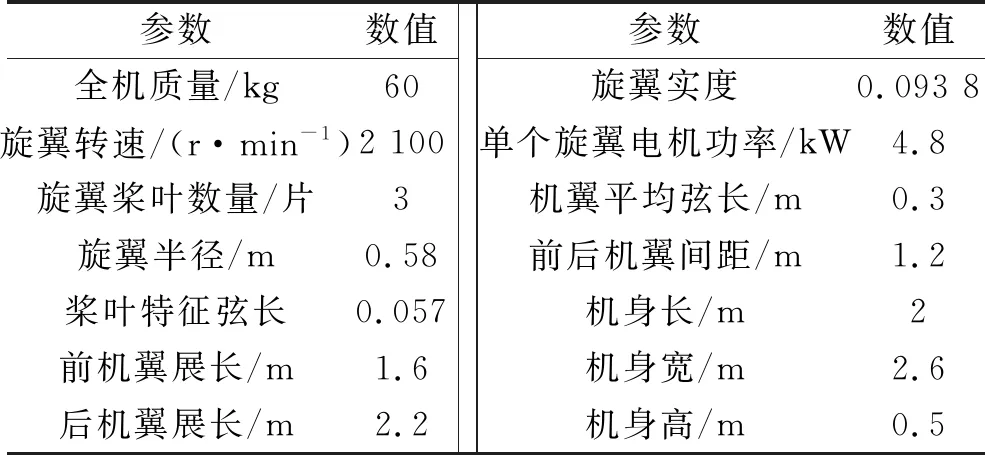
表1 倾转四旋翼飞行器总体参数

本文计算中采用的坐标系如图2所示,主要包括有地面坐标系ODXDYDZD、体轴系OXYZ、风轴系OWXWYWZW、旋翼轴固定坐标系OSXSYSZS等等。

图2 倾转四旋翼飞行器建模坐标系

1.1 旋翼模型

在进行旋翼建模时,4副旋翼只有旋向的区别,用符号Δ来区分,其他参数均相同。旋翼的诱导速度采用如下模型[16]

vi=

(1)

(2)

根据参考文献[17],可以得到旋翼在桨毂风轴系下的拉力TW、后向力HW、侧向力YW、扭矩Q、滚转桨毂力矩LW和俯仰桨毂力矩MW。通过坐标转换,在机体坐标系下作用于飞行器重心处的旋翼力和力矩为

(3)

(4)

1.2 机翼模型

倾转四旋翼飞行器飞行过程中,旋翼的下洗流直接冲击机翼的上表面,会产生较大的向下载荷。研究表明,倾转双旋翼中旋翼对机翼所产生的载荷能达到旋翼拉力的10% ～ 15%[18],该影响在直升机模式下尤为明显。由此可见,不能忽略旋翼对机翼的气动干扰。旋翼对机翼的干扰可以分为两个部分,如图3所示:①机翼受到旋翼尾流影响的部分,称为滑流区,图中阴影部分;②不受旋翼尾流影响的部分,称为自由流区。

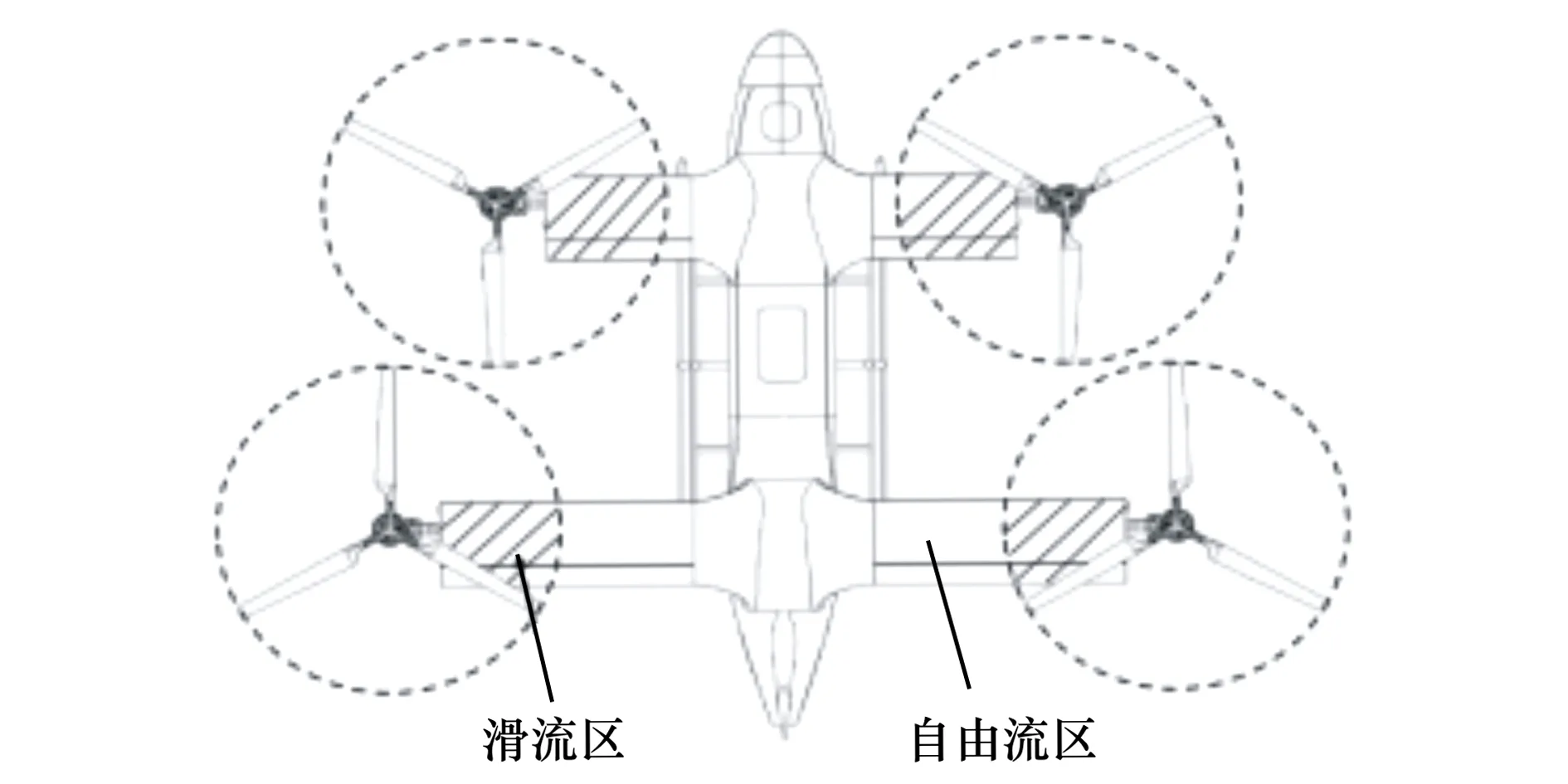
图3 旋翼对机翼的干扰示意图

机翼气动合力是由两部分气动力的叠加而成。为了计算2个部分的气动力,需要确定前后机翼滑流区和自由流区的面积,其面积可用以下公式进行计算[16]

SWFS=SW-SWSS

SSSmax=2ηSSRc

(5)

式中,下标WSS表示滑流区,下标WFS表示自由流区,μmax为旋翼尾迹偏出机翼的最大前进比,μ为旋翼的前进比,ηSS为旋翼滑流的修正因子,R为旋翼的半径,c是机翼的平均气动弦长,SW为机翼的总面积。

滑流区机翼的来流速度可表示为

(6)

式中：vi是旋翼的平均诱导速度；rWWS是滑流区的气动中心。自由流区的来流速度不考虑旋翼诱导速度的影响,根据来流速度可以计算出滑流区的动压qWSS和自由流区的动压qWFS。则整个机翼的力和力矩可以表示为

LW=qWSSSWSSCL,WSS+qWFSSWFSCL,WFS

DW=qWSSSWSSCD,WSS+qWFSSWFSCD,WFS

MW=qWSSSWSScCM,WSS+qWFSSWFScCM,WFS

(7)

式中：LW为机翼升力；DW为机翼阻力；MW为机翼俯仰力矩；CL,CD,CM为对应的升力系数,阻力系数和俯仰力矩系数。根据机翼的气动中心,可以计算得到机体坐标系中机翼产生的力(XW,YW,ZW)T和力矩(LW,MW,NW)T。

1.3 机身和垂尾模型

机身气动力计算比较复杂,本文的机身气动数据由CFD计算得到。根据机身的迎角和侧滑角,可得到气动力系数为CLF,CDF,CYF和力矩系数为CRF,CMF,CNF。于是在机体坐标系下机身产生的气动力和力矩可表示为

(8)

(9)

(10)

(11)

式中：αVT为垂尾的迎角；βVT为侧滑角；iVT为垂尾的安装角；SVT为垂尾的面积。

1.4 模型验证

为了确定本文所建立模型的准确性,分别对单旋翼的拉力以及旋翼对机翼的干扰进行试验验证,试验装置如图4以及图5所示。

图4 单旋翼拉力试验 图5 旋翼对机翼的气动干扰试验

进行单旋翼拉力试验时,转速恒定2 100 r/min,分别在不同的总距输入下,得到需用功率随旋翼拉力的变化。进行旋翼对机翼的干扰试验时,总距维持在12°不变,在不同转速下测得机翼的下载荷相对于旋翼拉力的百分比。试验结果如图6及图7所示,其中实线表示计算值,虚线表示试验值。

图6 单旋翼需用功率随拉力的变化

图7 机翼下载荷百分比随旋翼拉力的变化

从图中可以看出,模型计算的结果与试验值吻合比较好,说明本文建立的飞行动力学模型较为准确。在悬停状态下,机翼的下载荷占旋翼拉力的12%～13%左右。

2 直升机模式操纵策略与配平计算

根据飞行器质心的运动学和动力学方程,配平时可以确定6个未知变量,包括4个操纵输入变量和2个姿态角变量。倾转四旋翼飞行器的操纵输入众多,直升机模式下,4副旋翼的操纵控制变量多达12个,每副旋翼都可以进行总距、纵向周期变距和横向周期变距操纵。显然,待求解的未知量个数多于方程的个数。本文提出了一种倾转四旋翼飞行器直升机模式下的操纵策略,解决了倾转四旋翼飞行器直升机模式下的操纵冗余问题。

2.1 直升机模式操纵策略

直升机模式下,倾转四旋翼飞行器的运动既可以用总距的联动与差动控制,也可以用总距联动与周期变距控制。本文所使用的操纵策略为总距联动和差动以及周期变距差动的组合方式,即通过四副旋翼的总距联动δver来实现垂向操纵,通过左右旋翼总距的差动δlat来实现横向操纵,通过前后旋翼总距差动δlon来实现纵向操纵,通过前后旋翼横向周期变距差动δyaw来实现航向操纵,则操纵输入的控制变量δ可以表示为

δ=[δver,δlat,δlon,δyaw]T

(12)

将这4个操纵量分配到每一副旋翼上,从而可以得到每一副旋翼总距、纵向周期变距和横向周期变距的大小,分配关系如表2所示。

表2 每副旋翼的操纵量大小与操纵输入控制变量的关系

经过上述操纵量的分配,可以将4副旋翼的12个操纵量转化为4个,从而在进行配平计算时,可以得到唯一解。

2.2 配平计算

进行配平计算时,飞行器的飞行高度为50 m,重心位置O位于机体构造基准线上并在两倾转轴纵向位置的中点。根据参考文献[19]对倾转四旋翼飞行器过渡走廊的研究,在固定翼模式下飞行器飞行的最小速度为28 m/s,因此,本文在进行相关计算时,直升机模式下的最大速度为30 m/s。配平结果如图9所示。其中,φ表示滚转角,θ表示俯仰角。

图8 直升机模式配平结果随速度的变化

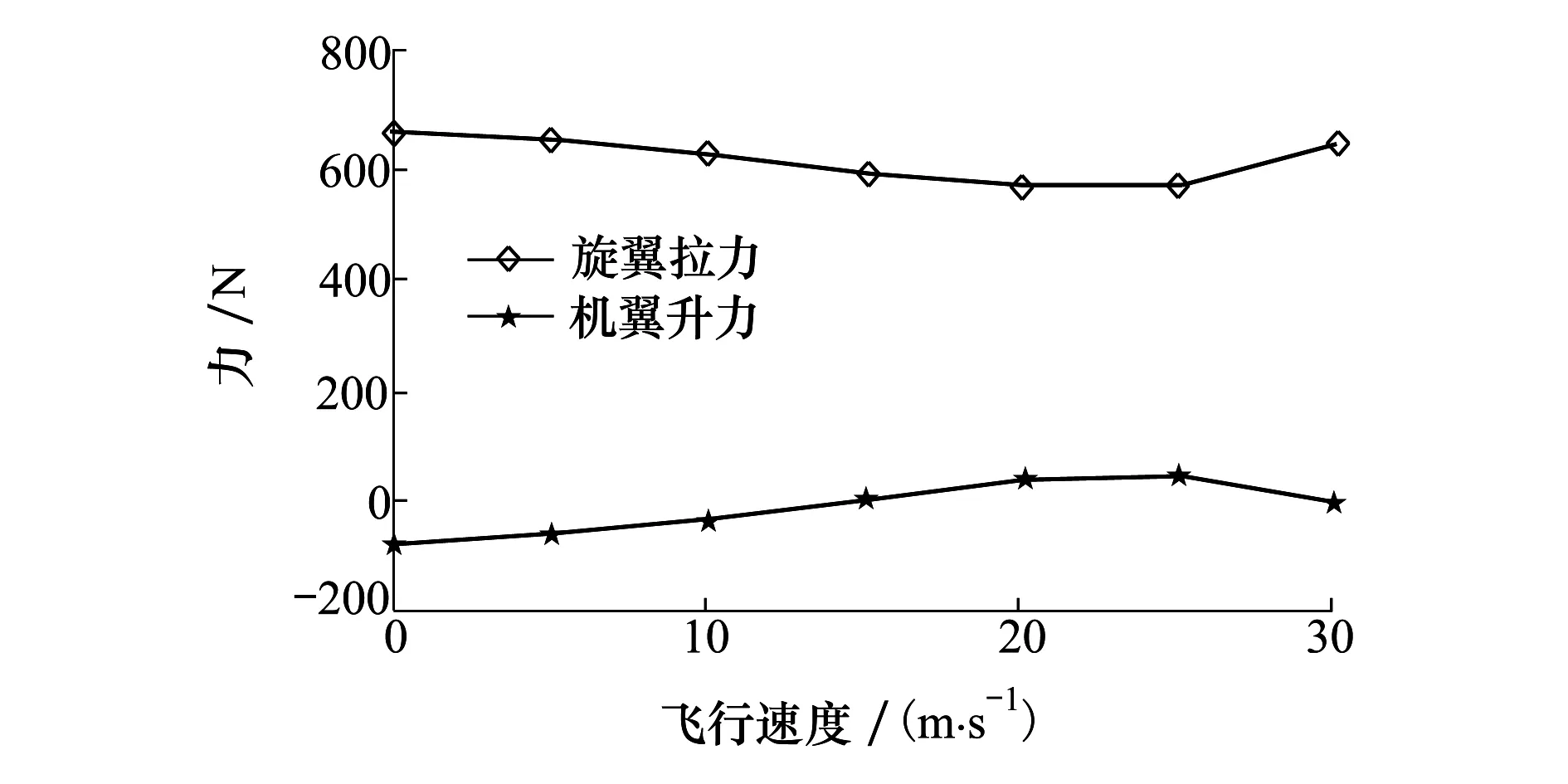
图9 直升机模式下旋翼拉力和机翼升力随速度的变化

图8a)反映了配平状态下操纵输入随速度的变化,可以看出,随着飞行器飞行速度的增加,总距联动的配平值先减小后增大。这是由于飞行器前飞时,旋翼的入流比先减小后增大。在相同的总距下,入流比减小,拉力值增大,从而产生相同拉力时,总距有所减小,该变化趋势与常规直升机前飞时相同。其他3个通道的操纵输入接近于零,这是由于重心选取在两倾转轴的中间造成的,4副旋翼产生的俯仰力矩和滚转力矩基本上相互抵消,并且不会产生偏航力矩。图8b)是滚转角和俯仰角配平值随速度的变化,其中滚转角的变化基本为零,俯仰角的值随着速度的增大不断减小。这是因为飞行器前飞速度越大,阻力越大,此时,飞行器需不断低头使旋翼产生更大的纵向分力以克服阻力。在倾转四旋翼飞行器飞行的过程中,机翼处于旋翼的下洗流中,直升机模式下旋翼的拉力和机翼的升力随速度的变化关系如图9所示。从图中可以看出,在悬停状态时,机翼升力为负值,方向向下,这是由于旋翼尾流对机翼的干扰造成的,并且悬停状态下干扰最为强烈。随着速度的增加,该干扰的影响逐渐减小,因为旋翼尾流在机翼上的干扰面积在减小。

机翼的升力随速度的变化趋势为先增大后减小,由于来流的增大,旋翼下洗流减小,引起机翼的迎角增大,且动压增加,从而升力增大。当到一定速度时,机身低头严重,导致机翼迎角减小,升力减小。

3 操纵性与稳定性

操纵性和稳定性是倾转四旋翼飞行器非常重要的飞行力学特性。飞行器的操纵性即为操纵响应,指飞行器对操纵输入后的反应。评价飞行器操纵性指标有操纵功效,操纵耦合等。如何使飞行器在完成相应的飞行动作时,驾驶员的操纵简单省力是研究操纵性的目的。稳定性是指飞行器抵抗外界干扰并保持其原有状态的能力。稳定性可以用飞行器的稳定性导数和特征根加以分析。

3.1 操纵功效与操纵耦合

操纵功效解释为单位操纵输入时,所引起重心处力或力矩的改变量。对于垂向通道操纵,为垂向力改变量,而其他通道为对应力矩的改变量。过小的操纵功效会使飞行器不易改变飞行状态,甚至导致飞行器在该通道的操纵失效。由于倾转四旋翼飞行器各部件气动力的复杂性,某一通道的操纵输入会引起其他通道力或力矩的变化,即操纵耦合。

图10～13反映的是不同通道单位操纵输入下,操纵功效和操纵耦合随速度的变化。其中ΔX表示纵向力变化量,ΔY为横向力变化量,ΔZ为垂向力变化量,ΔL表示滚转力矩变化量,ΔM表示俯仰力矩变化量,ΔN表示偏航力矩变化量。实线代表力的改变量,虚线代表力矩的改变量。

图10 垂向输入下的操纵功效与操纵耦合 图11 横向输入下的操纵功效与操纵耦合

从图10a)中可以看出,垂向操纵功效的大小在小速度时基本不变,随着速度进一步增加而逐渐增大,这是由于旋翼拉力的变化跟旋翼入流比和前进比都有关系,如(13)式所示

CTW∝(-λ,μ2θ0)

(13)

式中，θ0表示总距。当旋翼总距增大时,入流比也会增大,在小速度时,(13)式中第二项增加的量没有第一项减小的量多,导致拉力有所减小。随着速度增加,第二项增加的量占主导作用,从而操纵功效不断增大。图10b)为垂向操纵引起的操纵耦合,可以看出,随着速度的增加,纵向力和俯仰力矩的大小不断增大。这是由于飞行器前飞时,旋翼会后倒,此时垂向操纵引起的拉力增量在X轴上产生负的分量,并且速度越大,旋翼后倒越大,该分量值大小也越大。图11a)和图12a)反映的横向输入下的操纵功效和纵向输入下的操纵功效变化,其规律与垂向类似,主要是因为横向输入及纵向输入都是旋翼总距的差动,且重心处于前后旋翼及左右旋翼的对称位置,则俯仰力矩的变化和滚转力矩的变化与垂向力的变化一致。图11b)为横向输入下引起的操纵耦合,可以看出偏航力矩的大小随速度的增大而增大,这也是由于飞行器前飞时,旋翼后倒,左旋翼(编号1和4)在横向操纵下拉力增大,产生后向力;而右旋翼(编号2和3)拉力减小,产生前向力。因此,4副旋翼会形成负的偏航力矩,且该力矩的大小随前进比的增大而增大。图12b)是纵向输入下引起的操纵耦合,由于左右旋翼产生的偏航力矩相互抵消,所以耦合基本可以忽略。图13a)为航向的操纵功效,其大小随速度的增大先减小后增大,该变化趋势与旋翼总距变化基本一致。因为在进行相同的横向周期变距时,总距较小时所产生的侧向力较小,从而,偏航操纵功效也会小。从图13b)可以看出,航向操纵下引起的操纵耦合很小。

图12 纵向输入下的操纵功效与操纵耦合 图13 航向输入下的操纵功效与操纵耦合

综上所述,倾转四旋翼飞行器在直升机模式时,针对本文的策略操纵,垂向、横向和纵向的操纵功效都很大,且只有垂向和横向有一定的操纵耦合。航向的操纵功效相对于其他通道比较小,可以考虑在速度增大时加入方向舵的操纵以提高航向操纵功效。

3.2 稳定性

飞行器的稳定性可以用稳定性导数和特征根进行分析。其主要稳定性导数包括有速度稳定性Mu、航向稳定性Nv、上反效应Lv、迎角稳定性Mw、垂直阻尼Zw、滚转阻尼Lp、俯仰阻尼Mq及偏航阻尼Nr。其求解方法是使用中心差分法,比如

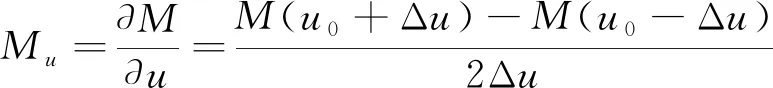
(14)

式中：uo表示基准状态下的初始值；Δu表示速度的增量。

特征根的确定需要求解飞行器在某一配平状态下的线化方程,线化的方法是利用小扰动理论。非线性方程线化为一阶微分方程的形式如(15)式所示

(15)

式中：x=[Δu,Δv,Δw,Δp,Δq,Δr,Δφ,Δθ,Δψ]T为状态变量增量；A为稳定性导数矩阵；B为操纵导数矩阵。根据稳定性导数矩阵A,可以求得飞行器在该飞行状态下的特征根。

图14反映的是不同速度下的主要稳定性导数变化情况。从图14a)中可以看出,速度稳定性Mu在小速度下值为正,是稳定的,主要是速度增加使旋翼后倒,从而产生抬头力矩使飞行器抬头减小速度的增加。但由于倾转四旋翼飞行器的后机翼面积大于前机翼,在速度增加到一定时,后机翼与前机翼产生的低头力矩大于旋翼后倒产生的抬头力矩,导致飞行器对速度是不稳定的。航向稳定性Nv随着速度的增加不断增大,说明航向稳定性不断增强,这主要是由于垂尾的作用。上反效应Lv的大小随速度的增大而略有增大,因为前进比越大,在相同侧向来流下,旋翼侧倒更厉害。迎角稳定性Mw的值也随速度的增大而增大,这也是由于后机翼面积大于前机翼面积造成的。迎角增大时,后机翼会产生更多的升力使飞行器低头,从而减小来流迎角。图15b)反映了各阻尼的大小随速度的增加而增大。当飞行器速度增加时,即前进比增大,则相同角速度改变时,会引起更大的力矩阻碍其变化。

图14 主要稳定性导数随速度的变化 图15 特征根随速度的变化

特征根的分布也是分析飞行器稳定性的重要方法。根据(15)式中的稳定性导数矩阵A,可以确定9个特征根,每一个特征根对应着一种飞行器运动的模态。通过对其特征向量的分析可以确定不同特征根所属的运动平面。图15a)为纵向特征根随速度的变化,其中数字1代表纵向稳定模态,该模态随速度的增加稳定性增强,主要是因为旋翼和机翼的气动刚度和气动阻尼不断的增大。2代表悬停振荡模态或前飞浮沉模态。该模态随速度的增加有变稳定的趋势,且其频率不断减小,主要是由于飞行器对迎角的稳定性随速度的增大而不断增加。图15b)为横航向特征根随速度的变化。数字1对应的为滚转收敛模态,该模态的稳定性也与旋翼的刚度和气动阻尼有关。数字2对应的是悬停振荡模态和前飞时的荷兰滚模态,其悬停振荡模态与纵向悬停振荡模态类似,不过横航向还有垂尾的作用,由于垂尾在悬停时作用不大,该悬停振荡模态也是不稳定的。随着速度的增加,振荡模态演变成荷兰滚模态,但由于航向稳定性在前飞时变强,使得该模态的阻尼和频率随速度的增加而增大。数字3对应的是螺旋模态,该模态由上反效应和航向稳定性共同决定。在悬停时是稳定的,主要是上反效应的作用。随着速度的增加,航向稳定性不断增强,两者匹配关系发生变化,从而稳定性变坏。

4 结 论

1) 建立了倾转四旋翼飞行器的各部件的气动力模型,将旋翼的拉力以及悬停下旋翼对机翼的干扰的模型计算结果与试验进行了比较,结果吻合较好。

2) 针对倾转四旋翼飞行器直升机模式的操纵冗余问题,提出了一种操纵策略,并对飞行器进行了配平计算,其中总距的配平值随速度的增大先增大后减小,俯仰角的值随速度的增加不断减小。

3) 对倾转四旋翼飞行器的操稳特性进行了分析。操纵性方面:航向操纵功效相较于其他通道较小;垂向输入会引起的纵向力和俯仰力矩的耦合,横向输入会引起偏航力矩的耦合,且耦合值大小随速度的增加不断增大。稳定性方面:速度稳定性随速度的增加而变得不稳定;除螺旋模态外,其他模态随速度的增加稳定性增强。