一种具有正输出电压的无桥CUK PFC变换器
皇甫宜耿, 王爱本, 赵犇, 马雨辉, 马瑞, 夏磊
(1.西北工业大学深圳研究院, 广东 深圳 518057; 2.西北工业大学 自动化学院, 陕西 西安 710072)
随着化石能源的枯竭和日益严重的环境污染问题,以集中式、化石能源发电方式为主的传统电网正在向以分布式发电、清洁能源为主的智能电网转变。微电网是从传统电网向智能电网的过渡,开发和延伸微电网能够充分促进分布式电源与可再生能源的大规模接入[1]。微电网中有许多需要低压直流电源的应用场合,电能的传输、存储、离网[2],例如蓄电池充电、电解水制氢等。因此,非常有必要开发具有低输出电压和高效率的AC-DC变换器。桥式整流引起严重的电流谐波失真,因此功率因数校正(power factor correction,PFC)技术得到了快速发展。
传统的单相有源功率因数校正(active power factor correction,APFC)变换器由前级桥式整流电路和后级DC/DC电路组成,常用的DC/DC电路包括Buck、Boost、Buck-Boost、CUK、Sepic和Zeta电路[3]。Buck变换器具有一段死区时间,输入电流为零,这会导致较大的总谐波失真(total harmonic distortion,THD)和较低的功率因数(power factor,PF)[4-5]。Boost变换器由于输入电流连续和较低的输入电流THD等优点应用最为广泛,但其输出电压高于输入电压、不适合低压应用场合[6]。Buck-Boost变换器具有输入电流不连续、PF低的缺点[7]。Sepic变换器的缺点是输出电流不连续,从而导致高输出电压纹波[8]。CUK变换器的输入电流连续,纹波小,输出电压范围宽,已广泛应用于低压电源场合[9]。
传统的CUK PFC变换器的电流导通路径经过3个功率半导体器件,包括整流电路中的2个二极管和DC/DC电路中的1个开关管,增加了变换器的导通损耗,使其效率受到了极大限制[10]。文献[11]提出了3种新型的单相无桥CUK PFC变换器,它们可以减少电流路径中1个半导体器件,从而降低了导通损耗,但无桥CUK PFC变换器的输出电压为负,因此需要1个附加的反相放大器电路,这会增加变换器的尺寸和成本。而且,文献[11]所提出的3种变换器都有2个开关管,这增加了控制的复杂性。
为了减小变换器的尺寸和成本,参考文献[12]提出了一种新型无桥CUK PFC变换器,该变换器将所有开关管与二极管进行了翻转,不需要反相放大器电路,使输出电压为正。与文献[11]提出的无桥CUK PFC变换器相比,反相放大器电路被省去,从而减小了变换器的尺寸和成本。
本文提出了一种新型的无桥CUK PFC变换器。与文献[12]中的无桥CUK PFC变换器相比,开关管S1上方的2个二极管D3,D4被移至输入电感的后面,当开关管S1在输入电压的正半周期导通时,切断了输入电感L1和串联二极管D3的电流路径,从而减少了变换器的导通损耗。由于二极管位置的移动,每工频半周期内的2个工作电容可以减小到1个,并且二极管D3,D4从高频的大电流工作状态到工频的小电流工作状态,可以使用价格较为便宜的普通整流二极管代替价格相对较高的快恢复二极管,从而减小了变换器的尺寸和成本。
1 新型正输出无桥CUK PFC变换器工作原理分析及设计
1.1 新型无桥CUK PFC变换器工作原理分析
本文提出的新型的无桥CUK PFC变换器如图1所示,在分析提所出的变换器之前,假设所有器件都是理想的,并且变换器工作在不连续导通模式(discontinuous conduction mode,DCM)下。在交流输入电压的1个周期内,正负半周期的工作原理相同,因此仅在正半周期对工作原理进行分析,可以将其分为3种工作模态。定义D1为开关S1导通时的占空比,即t0~t1,D2是S1关断但二极管Do导通的占空比,即t1~t2。

图1 新型正输出无桥CUK PFC变换器
模态1 [t0~t1]:主要理论波形及模态1等效电路如图2和图3a)所示,在此模态下,开关管S1导通。二极管D1正向偏置,电源给电感L2充电,输出电感Lo两端的电压为VC1-Vo。假设输入电容C1足够大,其电压在1个开关周期TS内被认为是恒定的。根据模态3中的电压关系,可以得到VLo=Vac(t),因此Lo充电斜率为Vac(t)/Lo。电感L2和Lo的电压电流关系为
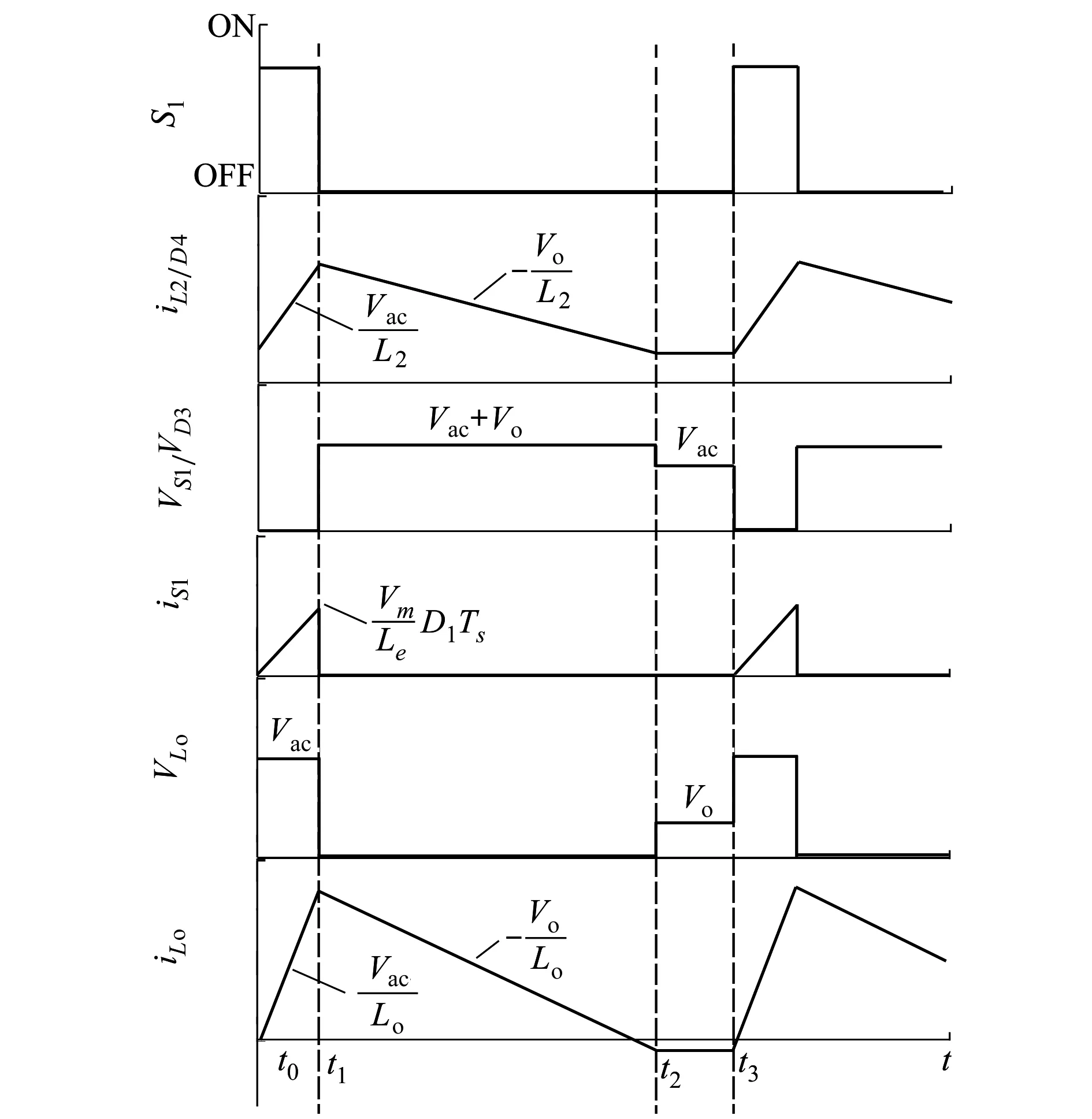
图2 一个开关周期内主要理论波形

图3 模态1~3的等效电路

(1)

(2)
流经开关管S1的峰值电流可以表示为
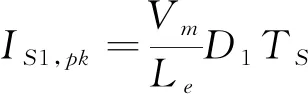
(3)
式中:Vm为输入电压Vac(t)的幅值;D1为开关S1导通时的占空比;Le为L1(L2)与Lo的并联等效电感。
模态2 [t1~t2]:在模态2中,开关S1断开,续流二极管Do导通。电感L2两端的电压为VC1-Vac(t),在模态1中,有电压关系:VC1=VLo+Vo,且VLo=Vac(t),所以得到VL2=Vo,因此电感L2开始以Vo/L2的斜率放电。Lo两端的电压等于Vo,以Vo/Lo斜率放电。放电完成后,二极管Do在零电流开关(zero current switching,ZCS)条件下关断。电感L2和Lo的电压电流关系为

(4)
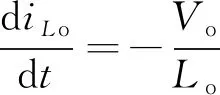
(5)
模态3 [t2~t3]:在此模态下,仅二极管D1和D4保持导通给电源和负载提供一个电流路径,此时,电感L2和Lo可以等效成电流源,电压为零。其电压关系为
VC1=Vac(t)+Vo
(6)
电源给电容C1充电,电容Co给负载供电。该模态一直持续到下一个开关周期TS开始。模态3持续的时间,即S1和Do都关断的时间为
toff=TS-ton-tdon
(7)
式中:ton是开关S1导通的时间,即t0~t1;tdon是输出二极管Do导通的时间,即t1~t2。
根据(2)式和(5)式,电感Lo在ton的充电电量等于在tdon的放电电量。占空比D1和D2的关系为

(8)
式中:M是电压转换比(M=Vo/Vm);ω是输入电压角频率。
1.2 新型无桥CUK PFC变换器的设计
1) 输入电感设计
如图2所示,输入电感L2以Vac(t)/L2的斜率充电,输入电流纹波ΔIL2为Vac(t)/L2与D1*Ts的乘积,可以得到输入电感L2的值(L1一样)
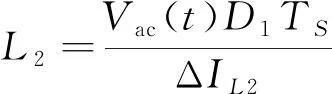
(9)
2) 电压转换比M
根据文献[12]提出的CUK PFC变换器的大信号模型,可以得到平均输入电流,在输入和输出端根据功率守恒,可以求得输入等效电阻,进而可以推出电压转换比M为[13]

(10)
3) CCM和DCM的界限[13]
为了确保所提CUK PFC变换器工作在DCM模式下,可以获得Ke的最小值和最大值,如下所示

(11)

(12)
这里Ke为

(13)
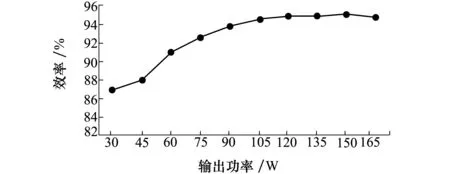
因此,当满足不等式Ke 4) 输入与输出电容的确定 要求输入电压频率fL远小于开关频率fs,谐振频率fr根据(15)式确定。可以确定输入电容C1的值。变换器输出纹波频率是输入电源频率的2倍。当半个周期内的输出电流全部由输出电容Co提供时,可以得到Co。 fL (14) (15) (16) 5) 开关管与二极管上的电压电流应力分析 基于图3,可以得到以下开关管和二极管的电压和电流应力表达式。 VD1,D2max=Vacmax (17) VD3,D4,Domax=Vacmax+Vo (18) VS1max=Vacmax+Vo (19) IDmax=IS1max=Iacmax+ΔIL (20) 式中:VD1,D2max是二极管D1和D2上的最大电压应力;VD3,D4,Domax是二极管D3和D4和Do上的最大电压应力;VS1max和IS1max分别是开关S1上的最大电压和电流应力;IDmax是所提CUK PFC变换器二极管上的最大电流应力;ΔIL是电感L1或L2上的电流纹波。 基于以上对所提新型的CUK PFC变换器的分析和设计,搭建了PSIM电路仿真模型,进行验证。具体仿真参数如表1所示。 表1 仿真参数 图4a)为输入电压电流波形,可以看出,输入电压电流同相位,保持了较好的正弦性;图4b)是开关S1满载时的电压和电流波形,开关S1在ZVS条件下导通;图4c)是输出二极管Do的电压和电流波形,可以看出Do在ZCS条件下关断。控制所提CUK PFC变换器工作在DCM模式下可以降低变换器的开关损耗。 图4 仿真波形 表2给出了所提CUK PFC变换器所用器件的型号和参数。实验平台如图5所示,包括主电路、驱动电路、控制器、电压差分探头、高频电流探头和功率分析仪等。控制功能通过dSPACE实现,由于变换器工作在DCM模式下,省去了电流控制环,只需要1个电压外环,采集输出电压信号,反馈到dSPACE中,与给定参考电压比较,得到误差信号,通过PI调节后得到输出占空比,从而保证变换器输出电压的稳定性。 表2 器件型号参数 图5 CUK PFC变换器实验平台 实验结果与仿真结果吻合,开关S1在ZVS条件下开通,Do在ZCS条件下关断,分别如图6a)、6b)所示。从而减少了变换器的开关损耗,提高了变换器的效率。 图6 满载时开关S1 ZVS导通与二极管Do ZCS关断 图7a)至7c)是变换器分别带载100%、50%和30%的输入电压和电流波形。满载时输入电流THD为3.78%、PF为0.995 7。随着负载的减小,输入电流幅值变小,正弦性变差,带载30%时正弦性最差,满载时正弦性最好。图8是所提变换器在不同输出功率下的效率折线图,最差效率为输出30 W时的86.05%,最高的效率为输出150 W时的94.86%。 图7 不同负载下输入电压电流波形 图8 所提变换器的在不同输出功率下效率图 提出了一种新型无桥CUK PFC变换器拓扑,无需附加反向放大器电路即可使变换器输出电压为正,通过优化拓扑,减少了1个输入电容。该变换器工作在DCM下,不需要电流控制环,从而简化了控制电路。此外,所提出的变换器前级4个二极管都工作在工频小电流工作状态,可以选择普通整流二极管代替快恢复二极管,进一步减小了变换器的体积和成本。对所提无桥CUK PFC变换器的工作原理进行了理论分析,仿真和实验验证。实验结果表明,开关S1在ZVS条件下导通,输出二极管Do在ZCS条件下关断,从而降低了开关损耗,提高了变换器的效率。变换器满载时PF为0.995 7,输入电流THD为3.78%,最佳效率为94.86%。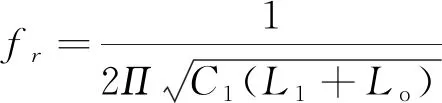

2 仿真结果分析


3 实验结果分析




4 结 论

