基于驾驶特性的ACC系统安全间距策略研究

施卫 万广轩 刘斌

摘 要：为自适应巡航控制系统（ACC）提出一种基于驾驶特性的行车安全间距策略，在分析对比现行CTH和VTH算法各自的优劣后，考虑驾驶员动态跟车特性，以此为基础对VTH算法进行改进设计。在Matlab/Simulink和Carsim联合仿真平台下使用经典PID控制算法设计的ACC系统上层控制器对CTH、VTH及本文改进VTH策略进行稳态波动速度、急加/减速、恒定车速的复合工况仿真对比。结果表明，基于驾驶特性设计的改进VTH能够在传统VTH及CTH之间获取良好的平衡性能，既能对前车速度激变做出快速响应，也能以平滑且较低的加速度跟踪期望加速度，保证舒适性。

关键词： 自适应巡航控制系统;动态驾驶特性;可变车头时距策略;期望安全间距

文章编号： 2095-2163（2021）01-0156-05 中图分类号：U461.91 文献标志码：A

【Abstract】This paper proposes a safe driving distance strategy based on driving characteristics for the design of the ACC system. After analyzing and comparing the respective pros and cons of the current CTH and VTH algorithms， considering the driver's dynamic following characteristics， the design of VTH algorithm is improved. Under the Matlab/Simulink and Carsim co-simulation platform， the upper-level controller of the ACC system designed by the classic PID control algorithm is used to focus on CTH， VTH， and the improved VTH in this paper to simulate the compound operating conditions of steady-state fluctuating speed， rapid acceleration/deceleration， and constant vehicle speed. The results show that the improved VTH designed in this paper can obtain a good balance performance between the traditional VTH and CTH. It can not only respond quickly to the sudden changes in the speed of the preceding vehicle， but also track the expected acceleration with a smooth and low acceleration to ensure comfort.

【Key words】Adaptive Cruise Control system; dynamic driving characteristics; VTH; expected safe spacing

0 引 言

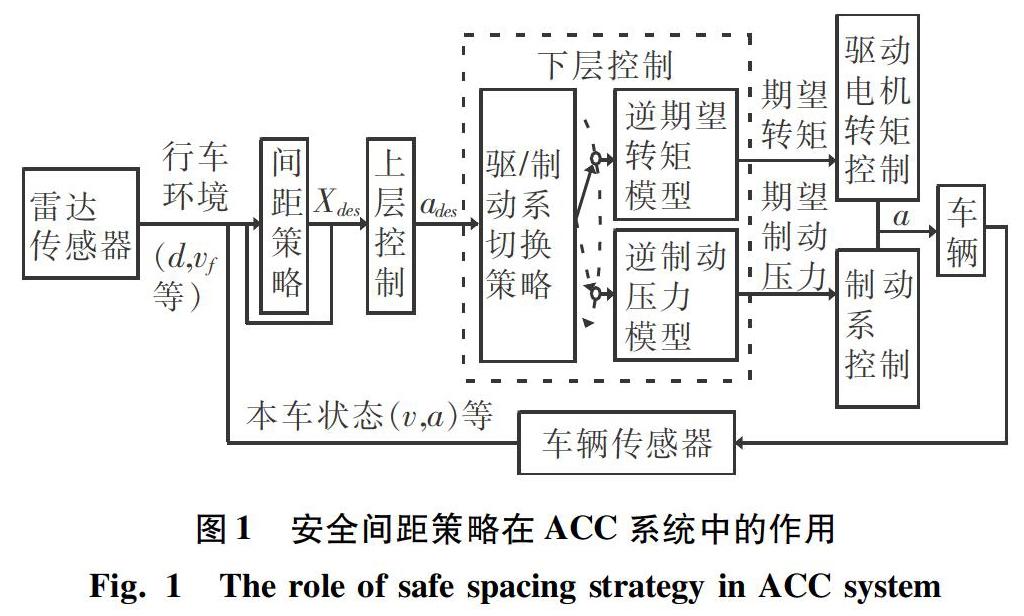
行車安全间距策略对自适应巡航控制系统（ACC）十分重要，任何ACC系统的开发都是从间距策略的选择和设计开始[1]，如图1所示。间距策略指的是连续两辆车之间的理想稳态距离，其选择和设计决定了在整个跟车模式中ACC的表现。在跟车模式工作时，行车安全间距策略根据传感器获取数据信息实时计算行车期望安全间距，安全间距过小会导致ACC车辆与跟车目标处于不安全状态，使驾驶员无法处理突发状况，精神紧绷，而过大的安全距离则会导致相邻车道的频繁变道，所以合适的行车安全间距策略是非常重要的。

1 行车安全间距策略分析

安全间距通常定义为在前车不可预测的行为下避免追尾碰撞的最小间隔[2]。在可变间距策略中，具有代表性的主要有基于车头时距的安全间距策略以及仿人间距策略（Human Factor Distance ，HFD），车头时距指的是在同一车道上行驶的车辆队列中，两连续车辆车头端部通过某一断面的时间间隔[3]。其中，基于车头时距的间距策略又可分为恒定车头时距（Constant Time Headway，CTH）策略和可变车头时距（Variable Time Headway，VTH）策略。

1.1 恒定车头时距策略（CTH）

最早起源于微观驾驶员行为提出的安全距离模型[4]：

其中，vf，vp分别表示自车和前车速度;λ1为车辆最大制动能力决定的参数;th为恒定车头时距，一般取值为1.5～2.8 s;dmin通常包括一个车身长度及车间最小距离，一般取值为4～6 m。因ACC车辆行驶过程中，前后车呈紧随状态，速度差异不大，将λ1（v2f-v2p）去除后简化可得：

分析式（2）可知，行车安全间距与自车车速成正比，其比值即为车头时距th，当车速越大，行车安全距离以正比例增益加大，用以避免因车速增加而同样大幅增加的刹车距离而导致的碰撞。但该模型假设车辆在制动机动的过程中具有相同且恒定的减速度，这种假设产生的解决方案可获得很高的减速度值，因此舒适度较低。

1.2 可变车头时距策略（VTH）

与CTH不同的是，在VTH策略中，th不再保持不变，而是随着周围的环境进行着相应的变化。Broqua[5]认为车头时距应与车速呈正增益关系，以此突出自车车速在行车安全距离模型中的重要性。具体公式可写为：

其中，λ2，λ3为参数，仅与自车车速相關，成正比例关系。

Yanakiev等人[6]认为还应注重前车车速在行车安全距离模型中的作用，具体公式可写为：

其中，vrel表示相对速度，vrel=vf-vp;t0，iv 为大于0的常数。

通过分析可知，上述策略在行车安全距离模型中考虑因素过于单一，当前车处于稳态驾驶过程中，还能得到较好的控制效果，但前车进行变加/减速行驶或频繁变速时，控制效果就不尽理想。

上海海事大学罗莉华在车头时距的计算中，引入前车加速度扰动代表前车速度的未来变化趋势[7]，得到如下形式：

其中，t0，iv，ia表示大于0的参数，ap表示前车加速度，研究推得其公式为：

为保证车头时距非负（确保安全性）且尽量节省交通流量，引入饱和函数后可得：

其中，sat（·）为饱和函数;thmax为车头时距上限值;thmin为车头时距下限值。

2 行车安全间距策略算法设计

通过对已有CTH和VTH策略算法分析可知，行车安全距离算法虽然并不复杂、计算量小，但其本身即存在着矛盾性，道路容量与车速成正比、与车间距离成反比，过多地减少车速和加大车间距离会导致交通效率的降低[8]，安全性要求需要与前车保持足够的间距，但过大的车间距离则会导致交通流量的浪费，以及可能更易致使其他车道车辆切入。故行车安全距离模型必须兼顾行车安全和道路交通效率两方面。CTH被证明在诸多复杂的形式环境下表现不尽理想[9]，而VTH策略在多名研究人员考虑不同因素的情况下所得出的行车安全距离算法也并不相同。本研究在上述分析的基础上，基于驾驶员跟车特性在常规VTH策略的基础上进行改进。

在实际驾驶过程中，行车安全距离不仅与自车车速相关，同时还与相对车速有密切的关联，因此需要在安全间距策略中考虑驾驶员的动态跟车特性[10]。

有加速度-位移公式：

由公式（8）可得行驶车辆以恒定减速度a从vx减速到0行驶过的距离为：

假设目前自车速度为vf m/s，前车速度为vp，两车都以相同的减速度进行制动，减速度常数为ac，则可得两车的制动距离：

其中，sf，sp分别表示自车和前车的制动到静止时行驶过的距离。

改进VTH策略示意如图2所示。当vp

则安全间距策略为：

但ACC系统大多数情况工作在稳定车流中，仿真结果显示这种考虑极端刹停工况的策略会对相对车速过于敏感，易造成交通流量的浪费，致使旁侧车道车辆切入工况增多。因此在该小节讨论的基础上对s进行改动，弱化其对相对车速的敏锐度，找到相对合适的平衡点，提出基于驾驶员动态跟车特性的VTH安全间距策略为：

其中，th表示车头时距;ac表示制动模型中减速度常数，取3m/s2;cv表示可变车头时距计算公式的常参数，经仿真比较取0.05;dmin表示最小安全距离，取6m。t0表示恒定车头时距值，文献[11]通过对交通流的实测分析将驾驶状态分为强跟驰状态和弱跟驰状态，这二者代表的最短车头时距和舒适车头时距分别满足以1.55s和2.60s为均值，以0.48s和1.13s为标准差的正态分布，其中舒适车头时距中包含了约1s的驾驶员心理裕值。综合考虑交通流量及安全性，车头时距取1.7s。

3 改进VTH的复合工况仿真分析验证

为验证本文提出的基于驾驶员跟车特性的改进VTH策略，采用经典PID算法设计上层控制器，Matlab/Simulink及Carsim搭建的联合仿真平台如图3所示，在该平台上进行复合工况仿真。并与式（2）所描述的恒定车头时距策略（CTH）、式（5）描述的可变车头时距（VTH）策略进行仿真结果对比。

文中采用稳态跟车小幅速度波动、急减速、急加速三种工况组成的复合工况对安全间距策略进行仿真实验。具体仿真实验设置为：仿真时长25s，前后车初始速度为20m/s、18m/s，初始间距40m;前车0～10s为近似稳态行驶，速度在20m/s左右小幅波动，10～15s为急减速工况，加速度为-1.6m/s2，15～20s为恒定车速行驶，20～25s为急加速工况，加速度为2m/s2。对各种状况下的实验结果可做阐释分述如下。

（1）0～10s的稳态小幅波动工况。该场景为ACC系统的主要工作场景，主要能够考察安全间距策略对ACC车辆速度和间距的跟踪能力。期望安全间距响应曲线见图4。由图4分析可知，因为初始车速前车大于后车，因此3种策略都采取了加速动作，伴随着前车的小幅减加速波动，这三种策略下的ACC车辆随即采取相应的减加速动作以跟随前车的速度变化。加速度响应曲线如图5所示。由图5分析可知，相较于该仿真中CTH策略，改进VTH对相对车速的变化具有更快的响应速度，由于前车的小幅减速变化，改进VTH在进行1.24s

处开始减速，而VTH和CTH分别为1.08s和1.58s，虽没有VTH响应速度更快，但却获取了更小的加减速度波动，不会因较小的相对车速变化而像VTH那样过度调节。进而得到，速度响应曲线如图6所示。图6中，自车速度响应曲线相较CTH与VTH更加平滑，同样体现了该改进VTH的优越性。

（2）10～15s、20～25s的急减/加速工况。这两种场景主要考察改进VTH策略对前车速度快速变化的响应能力以及跟踪能力，确保行车安全性。显然由图4可看出，当前车进行急减速时，改进VTH最先响应并减少相应的期望安全间距，且两车间实际间距响应曲线如图7所示。在图7中可知，自车加速度以较为平滑的减速度进行制动，而VTH的加速度变化较为突兀，会影响乘坐舒适度。

（3）15～20 s的恒定速度工況。该场景主要用于考察改进VTH策略对于加速度阶跃变化的响应能力。由图7中可知，伴随着减速度由1.6 m/s2突然转变为0 m/s2，VTH因为前车加速度ap的阶跃变化，产生了阶跃振荡，该情况同样也发生在20 s处工况由恒定速度工况转换至以加速度2 m/s2加速工况处。相比之下改进VTH能够以平滑的曲线进行过渡，而CTH因为只与vf相关，因此，相较其它两种策略表现出了一定的迟滞性。

4 结束语

上述仿真实验中，3种安全间距策略都能够完成最基本的跟车及安全性保障，但文献[4]中CTH策略因只考虑自车速度vf变化，过于保守，对于速度激变等场景难以适应，而文献[7]中VTH策略则将前车加速度ap作为扰动，虽能获取较好的速度激变响应，但却放弃了部分乘坐舒适性。相较之下，改进VTH在上述两者间获取了良好的平衡性，即能对前车速度激变做出快速的响应保证安全性，也能够以平滑且较低的加速度跟踪期望安全间距，保证舒适性。

参考文献

[1]RAJAMANI R. Vehicle dynamics and control[M]. 2nd ed. US：Springer，2012.

[2]DARBHA S， HEDRICK J K， CHIEN C C， et al. A comparision of spacing and headway control laws for automatically controlled vehicles[J]. Vehicle System Dynamics， 1994，23（1）：597-625.

[3]VOGEL K . A comparison of headway and time to collision as safety indicators[J]. Accident Analysis and Prevention， 2003， 35（3）：427-433.

[4]BRACKSTONE M， MCDONALD M . Car-following： A historical review[J]. Transportation Research Part F Traffic Psychology & Behaviour， 1999， 2（4）：181-196.

[5]BROQUA F. Cooperative driving ： Basic concepts and a first assessment of "intelligent cruise control" strategies[C]// Drive Conference Advanced Telematics in Road Transport. Amsterdam：Elsevier， 1991：908-929.

[6]YANAKIEV D， KANELLAKOPOULOS I . Nonlinear spacing policies for automated heavy-duty vehicles[J]. IEEE Transactions on Vehicular Technology， 1998， 47（4）：1365-1377.

[7]罗莉华. 车辆自适应巡航系统的控制策略研究[M]. 上海：上海交通大学出版社， 2013.

[8]侯德藻. 汽车纵向主动避撞系统的研究[D]. 北京：清华大学，2004.

[9]CHIANG Y H， JUANG J C . Longitudinal vehicle control with the spacing policy in consideration of brake input limits[C]// Proceedings of the IEEE International Conference on Systems， Mans and Cybernetics. Montreal， Canada： IEEE， 2007.

[10]袁伟， 付锐， 马勇， 等. 基于高速实车驾驶数据的驾驶人跟车模型研究[J]. 汽车工程， 2015， 37（6）：679-685.

[11]孟凡兴，张良，张伟. 驾驶员车头时距研究[J]. 工业工程与管理，2013，18（2）：131-135，140.