柱承式立筒排仓贮料侧压力地震响应试验研究

丁永刚 骆倩 许启铿 李学森 刘强

摘 要：为研究立筒排仓贮料对仓壁动态侧压力的地震响应规律，设计制作了缩尺比例为1∶25的柱承式立筒排仓和独立单仓模型，进行了3条地震波下不同地震动水准的振动台试验，分析获得两种模型的贮料地震响应特性、仓壁动态侧压力的变化规律与超压系数。研究结果表明：1）地震时仓内贮料与仓壁存在的相位差与仓体位置及测点位置相关;2）边仓与中仓仓壁动态侧压力的分布规律与地震波输入方向有关;排仓的超压系数总体上小于独立单仓;3）边仓的超压系数大于中仓，两者均大于规范采用值，现行规范中所采用的综合修正系数偏小;4）独立单仓不能全面反映立筒排仓的贮料地震响应特性，考虑排仓中不同位置单仓及地震作用方向进行仓壁结构的强度设计十分必要。

关键词：立筒排仓;振动台试验;地震响应;侧压力

中图分类号：TU312;TU399 文献标志码：A 文章编号：2096-6717（2021）03-0167-07

Abstract： In order to study the seismic response of group silos stored materials to the dynamic lateral pressure of the silo wall， column-supported group silos and independent single silo models with a scale ratio of 1∶25 were designed and manufactured， and shaking table tests with different ground motion levels under three seismic waves were carried out. The seismic response characteristics of the two models， the variation law of dynamic lateral pressure and over-pressure coefficient of the silo wall were obtained. The results show that： 1） during the earthquake， the phase difference between the storage and the wall of the silo is relevant with the position of the silo body and the location of the measuring point; 2） the distribution law of the dynamic lateral pressure on the wall of the side silo and the middle silo is relevant with the direction of seismic wave input; on the whole， the over-pressure coefficient of the silo is generally smaller than that of the independent single silo; 3） the over-pressure coefficient of the side silo is larger than that of the middle silo， both of which are larger than the values adopted by the code， and the comprehensive correction coefficient adopted in the current code is relatively small; 4） the storage seismic response characteristics of the vertical silo cannot be fully reflected only via the independent single silo， therefore it is essential to consider the different positions of the silo and the direction of seismic action to design the strength of the silo wall structure.

Keywords：group silos; shaking table test; seismic response; lateral pressure

筒仓是以贮料荷载为主的特种结构，荷载组合区别于一般的构筑物，起控制作用的永久荷载主要是筒仓的自重，可变荷载主要是贮料[1]。近年来，虽然筒仓在实际工程中得到了广泛应用，但由于各国规范[2-4]对地震作用下贮料荷载工况考虑得不够全面，其破坏现象时有发生[5-6]。地震作用时，非压密的贮料对仓壁产生的超压会造成筒仓结构的损伤破坏。现行相关规范中关于贮料的超压仅考虑了卸料等因素，所采用的综合影响系数2.0，没有重点考虑地震作用下贮料的超压。对于群仓来说，群仓中各单仓之间因位置和连接约束的不同会存在动力相互作用，使群仓中贮料与仓体的相互作用变得更为复杂，不再等同于单仓，而工程中将群仓简化为单一的筒仓来进行截面设计，会对仓壁结构的安全造成隐患。

近年来，诸多学者对地震作用下筒仓动态侧压力的分布规律等进行了一系列研究。Silvestri等[7]基于欧洲筒仓设计规范，考虑了贮料的水平剪切力，得出了地震作用下筒仓仓壁动态侧压力的计算公式，但该公式仅适用于平底筒倉。陈豪[8]利用有限元分析软件ANSYS，对筒承式单仓进行动力时程分析，提出最大动态仓壁压力产生于上部仓壁区域。Holler等[9]通过筒承式单仓的振动台试验，发现欧洲筒仓设计规范中关于地震作用下动态侧压力分布的规定更适用于深仓。施卫星等[10]对两个筒承式单仓模型进行了地震模拟振动台试验，对筒仓进行了非线性地震反应分析，得出了地震作用下煤仓动态侧压力的计算公式。马建勋等[11-12]建立了筒承式单仓仓内贮料的增量型内时本构关系，构建了其在地震作用下考虑贮料的运动特征、贮料与仓体之间的相互作用等因素的计算模型。杨建勇等[13]对柱承式单仓模型进行了地震模拟振动台试验，指出地震作用下筒仓的动态侧压力在仓壁顶部急剧增大。张华[14]、张逯见[15]对缩尺比例为1∶16的钢筋混凝土筒承式和柱承式群仓进行了振动台试验，结果表明，地震作用下动态侧压力最大值出现在中上部区域，且仓顶处的动态侧压力明显偏大。虽然相关学者对地震作用下筒仓仓壁动态侧压力问题展开了较多研究，但关于柱承式立筒群仓结构动态侧压力的研究却极少，开展的振动台试验更是不足。

为此，筆者以柱承式立筒排仓和独立单仓为研究对象，通过地震模拟振动台试验，对地震作用下排仓中各单仓与独立单仓的仓壁动态侧压力分布规律和超压系数的差异进行了深入研究。

1 试验概况

1.1 模型设计

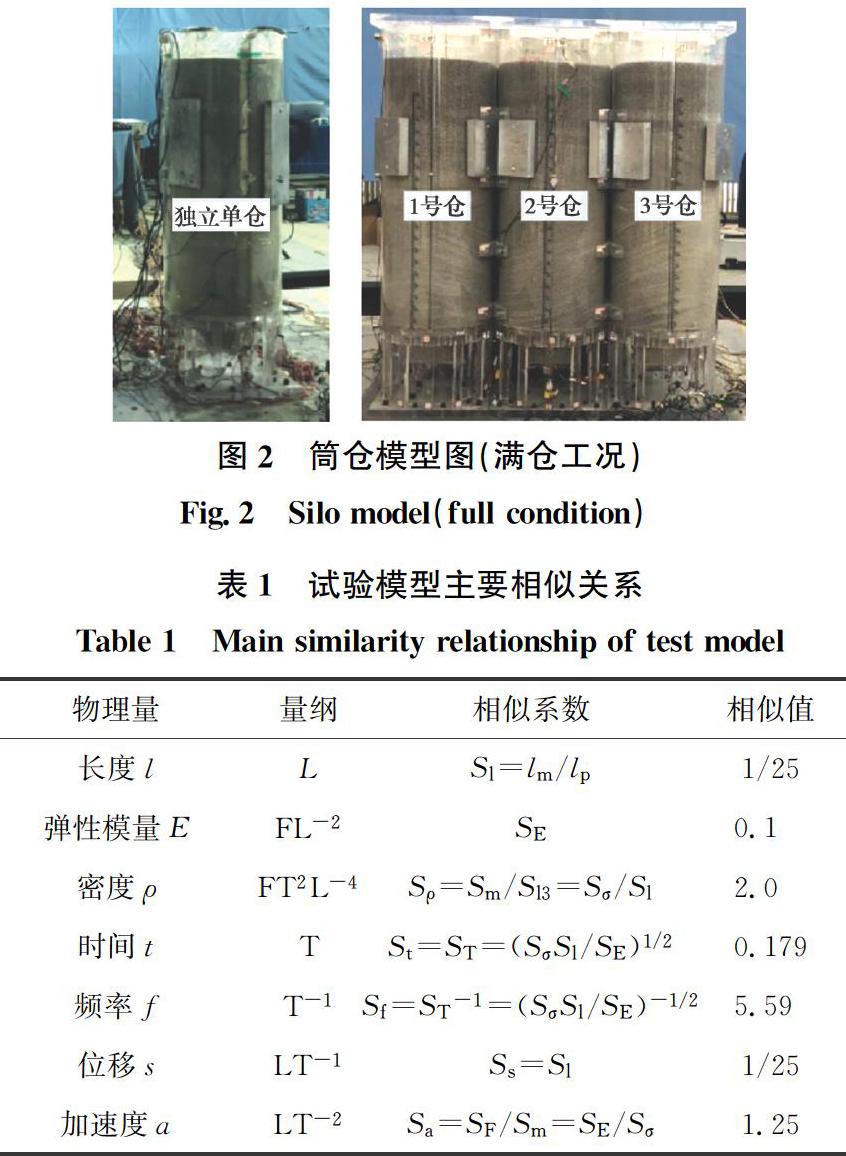
原型参照某粮库筒仓，根据现场试验条件，设计制作了缩尺比例为1∶25的柱承式立筒排仓（1×3组合）和独立单仓模型。模型总高度为1.62 m，其中筒仓仓体高度1.28 m，支承柱高度0.32 m，内径0.48 m，外径0.50 m，仓壁厚度0.01 m。排仓中的各单仓由仓体之间的连接件联为整体，两个单仓相切处对应的下部两个支承柱通过螺杆连接成一个整体，形成组合柱，顶板通过螺栓连接形成整体，底板与振动台台面的固定采用螺栓连接。模型尺寸如图1所示，满仓贮料状态下的模型实物如图2所示。

1.2 相似关系

按照相似理论[16]，基于模型的几何缩尺比例与材料性能比例，将模型的加速度相似比例系数取为1.25，其余各物理量均经过相似计算，主要相似系数见表1。

1.3 测点布置

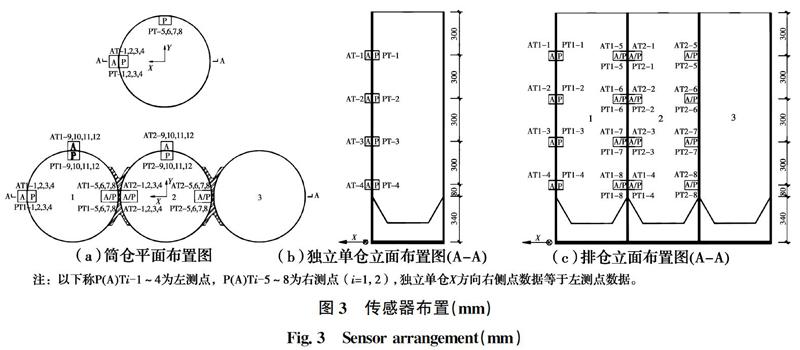
根据模型结构的对称性，选取排仓中具有代表性的仓体1号、2号仓作为试验的测试对象，1号、3号仓为边仓，2号仓为中仓。在独立单仓模型上沿振动台X方向共布置压力传感器4个，测点编号为PT1～PT4;为研究与压力传感器对应高度处仓体的动力响应，在仓壁上布置加速度传感器4个，测点编号为AT-1～AT4。在排仓模型上共布置压力传感器16个，测点编号为PT1-1～PT-8、PT2-1～PT2-8，同样在仓壁上布置加速度传感器16个，测点编号为AT1-1～AT1-8、AT2-1～AT2-8。在排仓模型上沿振动台Y方向共布置压力传感器8个，测点编号为PT1-9～PT1-12、PT2-9～PT2-12。具体测点布置如图3所示。

1.4 加载工况

根据原型结构所处的7度抗震设防烈度及Ⅳ类场地土类别要求，选用EL-Centro波、唐山波、人工波这3条地震波作为振动台台面激励。首先对筒仓沿振动台X方向输入地震波，然后再对筒仓沿振动台Y方向输入地震波。采用加速度峰值为0.062 5g、0.125g、0.159g、0.25g和0.281g等5个加载等级，同时，在各地震波输入前后对模型进行加速度峰值为0.05g的白噪声扫频。试验共设计42个工况，如表2所示。

2 试验结果与分析

根据振动台试验结果，首先分析排仓和独立单仓贮料的地震响应特性，进而分析其动态侧压力以及超压系数的差异。

2.1 贮料的地震响应特性

地震作用过程中，贮料之间及贮料与仓壁的运动和摩擦，会消耗一部分地震能量，贮料起到了一定的耗能作用。为了研究排仓中边仓与中仓及其与独立单仓的贮料地震响应特性及变化规律，进行了同一高度位置仓体加速度和仓壁动态侧压力的地震时程曲线分析。限于篇幅，仅对唐山波、加速度峰值为0.281g、边仓、中仓和独立单仓的右测点进行分析，其余各工况均可类似处理，其5个测点的加速度时程曲线和动态侧压力时程曲线如图4所示，其余测点时程曲线如图5所示。

规定地震作用过程中仓壁侧压力从静态值增加的动态值为增值，减小的为减值。从以上时程曲线图可以看出，动态侧压力总体分布在横坐标的上半部分，以增值为主;仓壁动态侧压力峰值发生的时刻滞后于仓壁加速度峰值发生的时刻，具体滞后情况见图6。

从图6可以看出：

1）仓壁动态侧压力峰值发生的时刻滞后于仓壁加速度峰值发生的时刻，并且，随着地震动的持续，相位差逐渐累加，说明地震时贮料在仓内的运动与仓体存在相位差，贮料与仓体存在动力相互作用。

2）地震作用时，排仓中贮料与仓体动力相互作用的强弱程度与仓体位置、测点位置相关。边仓和中仓右测点布置位置均接近仓体连接处，地震作用下中仓右测点的仓体底部在扭转效应及与相邻仓体的动力相互作用下，动力响应强于边仓。仓顶处独立单仓的相位差大于排仓中各仓体，仓底处后者相位差大于前者。地震作用时，仓顶部的贮料所受约束小，易于运动的贮料对仓壁的冲击较大;独立单仓仓底部的贮料被上部贮料压实，与仓壁的碰撞很小，而排仓因仓体间的动力相互作用使其动力响应在仓底部增强。

2.3 动态侧压力分布

为研究地震作用下边仓与中仓及其与独立单仓的贮料对仓壁侧压力的变化规律，根据振动台试验结果，对台面加速度峰值作用下仓壁动态侧压力增值和减值的数据进行分析。限于篇幅，仅考虑0.159g、0.25g、0.281g这3种工况，且取3条地震波增值及减值的平均值，得到的动态侧压力分布如图7、图8所示。

从图中可以看出：

1）动态侧压力增值总体上都大于减值，且随着台面输入加速度峰值的增大而增大。

2）对比图7可以发现：X方向上，边仓的左、右测点动态侧压力增值沿仓壁高度方向均大致呈现“上大下小”的分布形状，但分布图中左测点在仓体下部1/3范围增幅也相对较大。中仓的左测点呈现“中间大，上下小”的分布形状;而右测点呈现“中间小，上下大”的分布形状，与边仓测点的分布形状差距较大，表明动态侧压力增值的分布规律与筒仓所处位置呈相关性。独立单仓呈现与中仓左测点相似的分布形状，但分布图中两者最大值出现的位置不同，后者较前者更靠近仓体顶部。

对3级台面加速度峰值作用下边仓与中仓动态侧压力增值较独立单仓增大百分率的平均值进行分析。边仓左测点的增大百分率沿仓壁顶部至底部依次为90.8%、-55.6%、-2.7%、-6.8%;右测点的增大百分率沿仓壁顶部至底部依次为267.0%、114.9%、23.4%、-89.7%。中仓左测点的增大百分率沿仓壁顶部至底部依次为9.4%、104.3%、-34.3%、-9.0%;右测点的增大百分率沿仓壁顶部至底部依次为62.6%、-16.0%、-54.9%、403.6%。排仓中仓体位置的不同会引起仓壁动态侧压力沿仓壁高度分布规律的不同。

从增大百分率來看：排仓仓体顶部鞭梢效应较大，边仓、中仓的鞭梢效应强于单仓。边仓在平面上与其他仓体仅有一点约束，左测点布置位置远离连接处的部位，右测点布置位置接近连接处的部位，地震作用时右侧点与仓体间的动力相互作用使其动力响应增强。中仓在平面上与其他仓体有两点约束，左右测点布置位置均接近连接处的部位，其与仓体间的动力相互作用使动力响应在仓壁顶部1/3范围增强。

3）对比图8可以发现：Y方向上，边仓、中仓动态侧压力增值沿仓壁高度方向均大致呈现“上大下小”的分布形状;独立单仓则呈现“中间大，上下小”的分布形状。边仓动态侧压力增值较独立单仓增大百分率沿仓壁顶部至底部依次为154.0%、58.2%、-32.5%、-30.3%;中仓增大百分率沿仓壁顶部至底部依次为87.9%、-20.3%、-32.6%、-33.5%。

从增大百分率来看：X方向上的动态侧压力增值大于Y方向，说明X方向仓体整体刚度大于Y方向。边仓动态侧压力增值总体上大于中仓，地震作用时中仓所受的约束力大于边仓，故中仓整体动力响应弱于边仓。与独立单仓相比，边仓与中仓仓体顶部动态侧压力增值的增幅最为明显，地震作用时仓体顶部有一定的鞭梢效应，加之排仓中各仓体间的动力相互作用使其仓壁产生一定的扭转效应，故其鞭梢效应强于独立单仓。除仓体顶部，排仓动态侧压力增值总体上小于独立单仓，排仓中各仓体间的相互连接与约束，使其整体刚度较大，故动力响应小于独立单仓。

2.4 动态侧压力超压系数

定义超压系数为同一工况获得的各测点动态侧压力的绝对值与静态侧压力的比值。表3为超压系数的计算结果。

从表3可以看出筒仓的超压系数最大值均发生在沿仓壁高度方向上部1/3范围。超压系数总体上随着筒仓高度的增加而增加，呈逐步放大的趋势。

对比表中超压系数的最大值可以发现：1）在仓壁高度方向上部1/3范围内，边仓、中仓的超压系数均大于独立单仓。沿X方向，边仓左右测点的超压系数较独立单仓依次增大了12%、68%;中仓左右测点的超压系数依次增大了4%、16%。沿Y方向，边仓和中仓的超压系数依次增大了28%、16%。地震波输入时仓体间的动力相互作用使排仓仓顶产生一定的扭转效应，使其动力响应增强。2）边仓的超压系数大于中仓，表明排仓中贮料的地震响应特性与仓体所处位置呈相关性。值得注意的是，边仓仓体下部1/3范围超压系数明显大于其他仓体，这一规律尚未在其他相关研究中发现。3）地震作用下边仓与中仓仓体顶部1/3范围内贮料超压系数最大值均大于规范给出的考虑卸料、贮料的崩塌等因素采用的综合修正系数2.0，表明地震作用所引起的贮料超压不能忽略。且规范中规定的综合修正系数仅考虑了独立单仓的情况，并未考虑排仓结构的计算，在对排仓仓壁计算和结构设计时应该考虑对不同位置仓体分别进行计算。

3 结论

1）获得了柱承式立筒排仓和独立单仓的贮料地震响应特性。地震作用时贮料在仓内的运动与仓体存在相位差，并且随着地震动的持续，滞后相位差逐渐累加;排仓中边仓与中仓的贮料与仓体运动相位差存在不同，与测点位置相关。

2）揭示了地震作用下仓壁动态侧压力沿仓壁高度的分布规律。X方向上排仓中仓壁动态侧压力大于Y方向;边仓与中仓的仓壁动态侧压力沿仓壁高度分布规律不同;与独立单仓存在明显差异。独立单仓尚不能全面反映排仓结构在地震作用下的仓壁动态侧压力分布规律。

3）获得了地震作用下贮料对仓壁的超压系数。在筒仓上部1/3范围内，排仓仓壁产生的扭转效应使顶部测点动力反应加强，边仓、中仓超压系数均大于独立单仓;边仓超压系数大于中仓。排仓中各单仓和独立单仓超压系数均大于现行规范采用的综合修正系数。

4）现行规范中未考虑地震作用的仓壁超压计算方法是不合理的，也是偏于不安全的;仅依据独立单仓尚不能全面反映立筒排仓的贮料地震响应特性，提出了立筒排仓结构需要考虑其不同位置单仓及地震作用方向来进行仓壁结构强度设计。

参考文献：

[1] 钢筋混凝土筒仓设计标准： GB 50077—2017[S]. 北京： 中国计划出版社，2017.

Standard for design of reinforced concrete silos： GB 50077-2017 [S]. Beijing： China Planning Press， 2017. （in Chinese）

[2] 建筑抗震设计规范： GB 50011—2010 [S]. 北京： 中国建筑工业出版社， 2010.

Code for seismic design of buildings： GB 50011-2010 [S]. Beijing： China Architecture & Building Press， 2010. （in Chinese）

[3] Eurocode 8： Design of Structures for Earthquake Resistance-Part 1：General rules， seismic actions and rules for buildings： EN 1998-1-2004 [S]. 2004.

[4] American Society of Civil Engineers. Minimum design loads for buildings and other structures [M]. New York， NY： American Society of Civil Engineers， 1996.

[5] 蒋莼秋. 钢筋混凝土高架式贮仓震害综述[J]. 世界地震工程， 1987， 3（3）： 17-23， 51.

JIANG C Q.Summary of earthquake damage of reinforced concrete viaduct silo [J]. World Earthquake Engineering， 1987， 3（3）： 17-23， 51. （in Chinese）

[6] 清华大学， 西南交通大学， 重庆大学. 汶川地震建筑震害分析及设计对策 [M]. 北京： 中国建筑工业出版社， 2009.

Tsinghua University， Southwest Jiaotong University， Chongqing University. Earthquake damage analysis and design countermeasures of buildings in Wenchuan earthquake [M]. Beijing： China Architecture & Building Press， 2009. （in Chinese）

[7] SILVESTRI S， GASPARINI G， TROMBETTI T， et al. On the evaluation of the horizontal forces produced by grain-like material inside silos during earthquakes [J]. Bulletin of Earthquake Engineering， 2012， 10（5）： 1535-1560.

[8] 陈豪. 大直径预应力混凝土筒仓仓壁的受力有限元分析[D]. 武汉： 武汉理工大学， 2007.

CHEN Z H. Finite element analysis of large-diameter prestressed concrete silo[D]. Wuhan： Wuhan University of Technology， 2007. （in Chinese）

[9] HOLLER S， MESKOURIS K. Granular material silos under dynamic excitation： numerical simulation and experimental validation [J]. Journal of Structural Engineering， 2006， 132（10）： 1573-1579.

[10] 施卫星， 朱伯龙. 地震动下煤仓贮料侧压力研究[J]. 特种结构， 1993， 10（1）： 16-18.

SHI W X， ZHU B L. Study on lateral pressure of coal bunker under earthquake [J]. Special Structures， 1993， 10（1）： 16-18.（in Chinese）

[11] 马建勋， 梅占馨. 散粒体的增量型内时本构关系[J]. 土木工程学报， 1995， 28（3）： 17-22.

MA J X， MEI Z X. Incremental endochronic constiiutive relations for granular materials [J]. China Civil Engineering Journal， 1995， 28（3）： 17-22. （in Chinese）

[12] 马建勋， 梅占馨. 筒仓在地震作用下的计算理论[J]. 土木工程学报， 1997， 30（1）： 25-30.

MA J X， MEI Z X. Study on calculating theory of seismic response of silos [J]. China Civil Engineering Journal， 1997， 30（1）： 25-30. （in Chinese）

[13] 楊建勇.柱承式筒仓振动台试验研究及数值分析[D].辽宁 大连：大连理工大学，2018.

YANG J Y. Shaking table test and numerical analysis of column-supported silo [D]. Dalian， Liaoning： Dalian University of Technology， 2018. （in Chinese）

[14] 张华.立筒群仓结构模型模拟地震振动台试验研究[D]. 郑州：河南工业大学，2008.

ZHANG H. Shaking table test study on model simulation of vertical silo group silo [D]. Zhengzhou： Henan University of Technology， 2008. （in Chinese）

[15] 张逯见. 筒承式立筒群仓结构模型模拟地震振动台试验研究[D].郑州：河南工业大学，2010.

ZHANG L J. Shaking table test study on the structural model of tube-supported vertical silo group silo [D]. Zhengzhou： Henan University of Technology， 2010. （in Chinese）

[16] 周颖， 吕西林. 建筑结构振动台模型试验方法与技术[M]. 2版. 北京： 科学出版社， 2016.

ZHOU Y， LV X L. Method and technology for shaking table model test of building structures [M]. Beijing： Science Press， 2016. （in Chinese）

（编辑 章润红）