基于VOF 方法和DFBI 模型的溃坝水流数值模拟

马云飞，李涛，熊进标

上海交通大学 机械与动力工程学院，上海 200240

溃坝问题在计算流体力学(CFD)中由于其自由表面变化多样，常被用来验证数值模拟的可靠性。流体体积函数(VOF)方法和动态流体-刚体相互作用(DFBI)模型的结合多用于船舶工业设计等领域，其在模拟液体自由表面对船舶作用产生的多自由度运动问题中表现良好，基于此本文讨论了VOF 方法结合DFBI 模型处理溃坝冲击问题的数值模拟方法。

近些年来，国内对于溃坝问题的数值模拟方法进行了大量研究。其中，张力方等[1]将光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)和格子玻尔兹曼方法(lattice Boltzmann method，LBM)应用于溃坝问题并进行对比研究，结果表明：SPH方法在自由面捕捉方面有优势，LBM 在水位、压力等参数方面预测效果较好。王兴华等[2]针对溃坝过程中水位变化和溃坝负波对溃坝进程的影响进行研究，使用VOF 方法对溃坝水面流动状态进行数值模拟并与已有数据进行了比对验证。马利平等[3]采用源项法耦合了溃口演变模型DB-IWHR与基于GPU 加速技术的二维水动力模型，他们建立的耦合模型所得结果与实测吻合较好。陈本毅等[4]基于自主研发的紧致插值曲线数学模型研究了溃坝水槽闸门不同抽离方向的影响。曹引等[5]基于结构化网格建立了有限体积模型Hydro M2D，其在复杂地形和不规则边界情境下可以较好地模拟溃坝问题，并就此进行了各方面验证。王笑等[6]、王福良等[7]、董俊哲等[8]都对溃坝数值模拟方向有一定研究成果。可见对于溃坝问题的数值模拟研究成果十分丰硕，但是关于溃坝冲击效应问题的数值模拟方法却较为匮乏。

张力方等[1]研究了SPH 方法和LBM 方法对可运动障碍物位移的模拟，2 种方法均有一定效果。杨哲豪等[9]采用有限体积法和中心迎风格式建立了二位数值模型，该模型在模拟全局溃坝工况方面有良好表现，但却无法模拟实际水流紊动过程。

基于此，本文使用商用CFD 软件Star-CCM+的Overset 网格技术，结合VOF 和DFBI 模型模拟了挡板溃坝问题，还设计了挡板溃坝实验，运用高速可视化装置测量了溃坝液位变化及挡板摆角变化，为进一步验证该数值模拟方法，结合实验数据进行了研究分析。

1 控制方程

1.1 基本控制方程

挡板开启过程满足Navier-Stokes 方程，即

式中：v为t时刻的速度矢量，ρ为密度，p为压力，γ为运动黏度。

1.2 DFBI 模型

为了准确模拟挡板的运动，需要运用DFBI 方法。DFBI 模型用于模拟刚体响应流体施加的压力和剪切力，其控制方程为

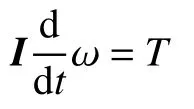
式中：T为挡板的净扭矩；ω是关于旋转轴的角速度；I为关于旋转轴的惯性矩，其展开式为

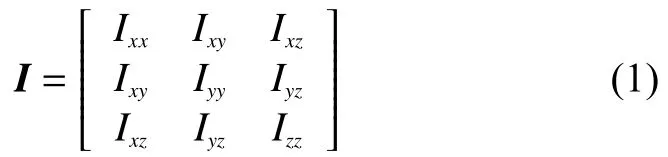
扭矩T主要取决于水流的压力扭矩Tp和剪切力转矩Tτ，满足

式中：f为水流所作用的表面，pf为作用在表面f上的压力，τf为作用在表面f上的剪切力，rf为挡板质心到面f中心的距离向量，αf为面f的面积向量。

考虑到实验装置尺寸不小，仅挡板就有近1 kg，摩擦力矩可以忽略不计，认为摩擦转矩为0。DFBI 模型仅以建立刚体质心的运动来得到整个刚体的运动，简单、有效且方便，但DFBI 模型不适用于刚体质心保持不变的情况。

1.3 VOF 方法

VOF 方法[10]是通过研究网格单元中流体和网格体积比函数来确定自由面，追踪流体的变化，而不是追踪自由液面上质点的运动。其在网格上该相流体质点存在的定义函数如式(2)，质量守恒形式如式(3)，差分形式如式(4)，差分网格如图1 所示。

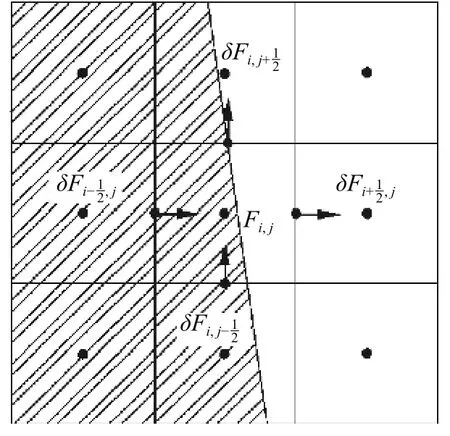
图1 网格单元上的变量表示[6]

VOF 方法形式简单，结果有效，在经过许多发展和改进后能处理越来越复杂的问题，自由面模拟结果也越来越精确，在多个不同领域发挥着重要作用。

2 实验设计

挡板溃坝实验装置的几何尺寸如图2 所示。实验装置通体为有机玻璃所制，左侧水箱内尺寸为300 mm×300 mm×300 mm，右侧蓄水池内尺寸为290 mm×350 mm×600 mm，挡板尺寸为320 mm×320 mm×10 mm，质量为1.21 kg。实验中，采用高速相机(Phantom V710)在挡板侧面和挡板正面分别进行观测。拍摄过程频率为500 Hz，图片分辨率为1 280 px×800 px。在水箱左侧外表面设置了标尺以确定最高液位。对于挡板摆角，取挡板外表面末端像素点作为参考点，根据其在运动过程中关于初始状态挡板外表面和经过外表面轴端点水平线的相对垂直距离得到摆角两直角边，使用反正切三角函数得到摆角值。本文就初始液位为100、150、200 mm 的3 个工况开展了观测实验。

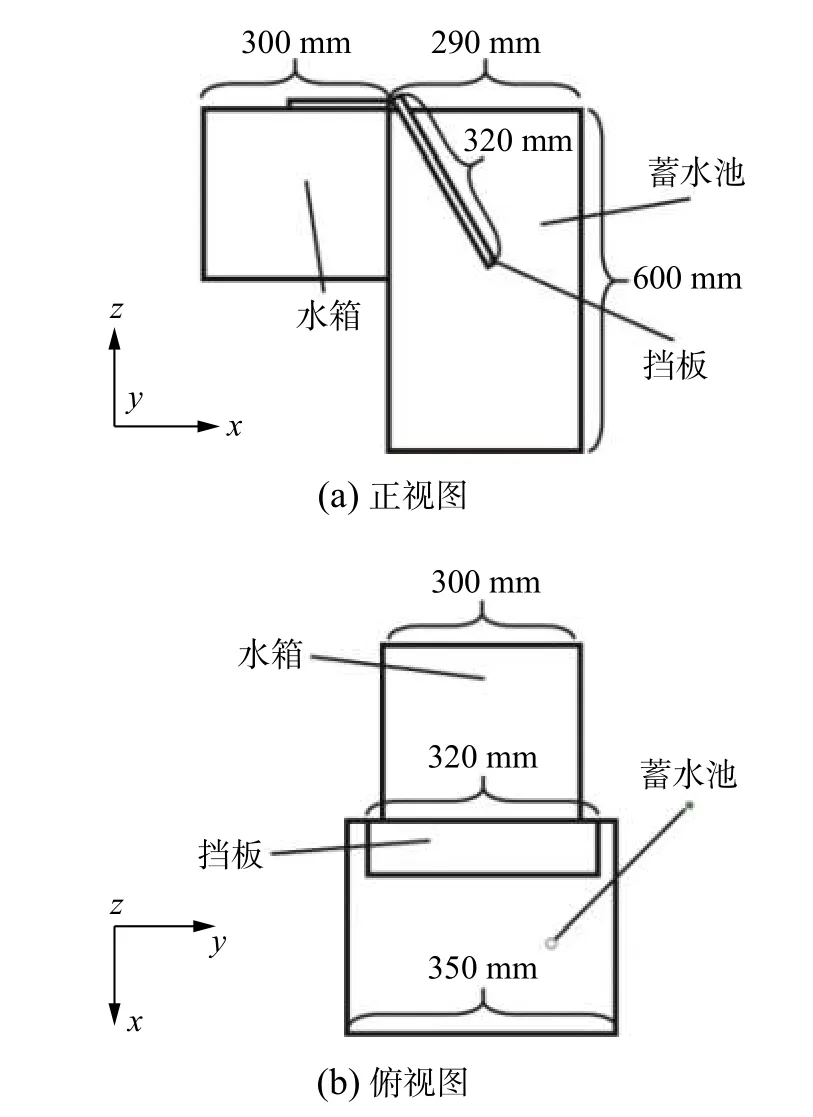
图2 实验装置

3 网格与物理模型

整个计算域由Overset 网格区域和背景网格区域组成：左侧背景网格区域尺寸为300 mm×300 mm×300 mm；右侧为Overset 网格运动的背景网格区域，其面积大于Overset 网格运动过程中扫过的区域面积，尺寸为290 mm×350 mm×325 mm；挡板垂直置于左侧箱体侧面，且高于箱体边缘10 mm。

左侧背景网格区域上表面和右侧背景网格区域下表面设为压力出口边界。在挡板周边设置Overset 边界，形成外尺寸为350 mm×340 mm×50 mm的Overset 网格区域，并与背景区域之间形成Overset 网格界面，使用紧密接近和代替孔切削设置。图3 为以Y轴为法向经过挡板几何中点截面的网格场景。Overset 网格与背景网格均以局部结构化网格处理，采用切割体网格外加棱柱层，网格尺寸为7 mm，注意Overset 网格尺寸需与背景网格尺寸尽量保持一致，否则在受体网格单元层的数据插值精度将受到影响。对溃坝流体主要活动区和挡板运动掠扫区域这2 个重点区域特意进行了局部网格加密。使用体积控制加密，其网格绝对尺寸为5 mm 与2.5 mm。生成背景区域85.8 万网格，重叠区域16.2 万网格。

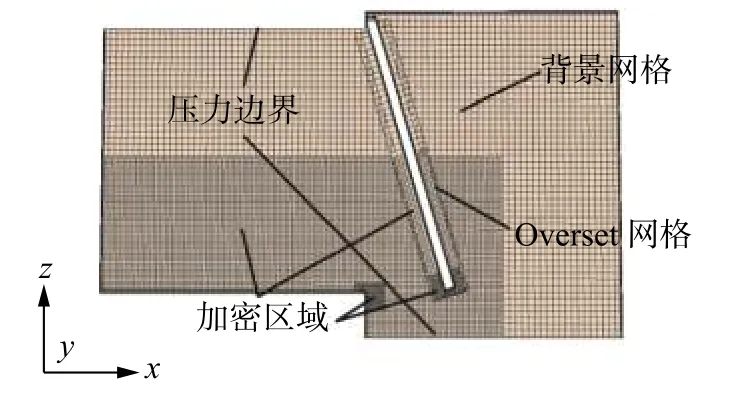
图3 网格与几何条件

物理模型采用可实现的双层k-ε湍流模型与VOF 流体域体积方法，外加重力影响。挡板设置DFBI 单自由度旋转运动，旋转轴设于挡板上表面中线，方向为-Y轴方向，质心为挡板几何中心，惯性矩对角分量根据式(1)计算。

隐式不定常设置为一阶时间离散，由于受体网格单元层会根据刚体运动更新边界，原则上在一个时间步长内刚体运动最大距离为网格单元尺寸。设置时间步长为0.002 s。为了每个时间步长内部迭代收敛完全，将最大内部迭代次数设置为20，最大物理时间设置为3 s。

4 模拟结果与分析

4.1 网格敏感性

为了分析网格敏感性，于初始液位150 mm 工况下加密区域网格，分别采用了3 种不同的基础尺寸，即0.006 m/0.003 m、0.005 m/0.002 5 m、0.004 m/0.00 2 m(采用较大尺寸标识)。图4 为挡板摆角和最高液位对网格的敏感性。

图4 最高液位与挡板摆角的网格敏感性

从挡板摆角来看，网格尺寸对模拟结果精度有一定影响。与0.006 m 网格相比，0.005 m 网格、0.004 m 网格结果有些许偏差；而0.004 m 网格结果显示与0.005 m 网格结果相差无几。从溃坝最高液位来看，网格尺寸越小，曲线越平滑。3 种网格尺寸情况下，网格越细越接近实验值，最高液位对网格尺寸要求较高。综合考虑精度和计算效率，模拟取加密区域0.005 m 网格尺寸计算较为合适。

4.2 计算结果验证

挡板溃坝实验中，溃坝水流泄出箱体，水流静压力作用在挡板上，挡板受到溃坝水流冲击产生旋转，在脱离冲击后，挡板受重力作用开始做回复运动，在回复至一定角度受到溃坝水流泄出形成的溃坝水流冲击，如此周期往复，如图4(b)中摆角运动曲线。以下将以第一、二周期的方式来表述振荡峰所在周期。

为了验证模拟的有效性，需要将实验结果与模拟结果进行比对。图5 为在初始液位150 mm工况下，t=0.2 s 时，实验和模拟在同一时间节点下的Y轴方向视角液位曲面形状与挡板运动状态的比对结果。图6 为在初始液位150 mm 工况下，t=0.2 s 时，-X轴方向视角液位曲面形状的实验和模拟结果。图5 和图6 中能明显观察到溃坝水流泄出时镜面水舌[11]两侧在前视窗上产生的液膜和完全润湿区域。

图5 Y 轴方向视角可视化结果示意

图6 -X 轴方向视角可视化结果示意

图7 为挡板角速度曲线，图8 为初始液位150 mm 工况下，挡板受力、力矩图。由图7 和图8 可以清晰地观测到受力和力矩曲线有4 个峰，表明溃坝挡板受流体的影响具有周期性，且逐渐减弱。

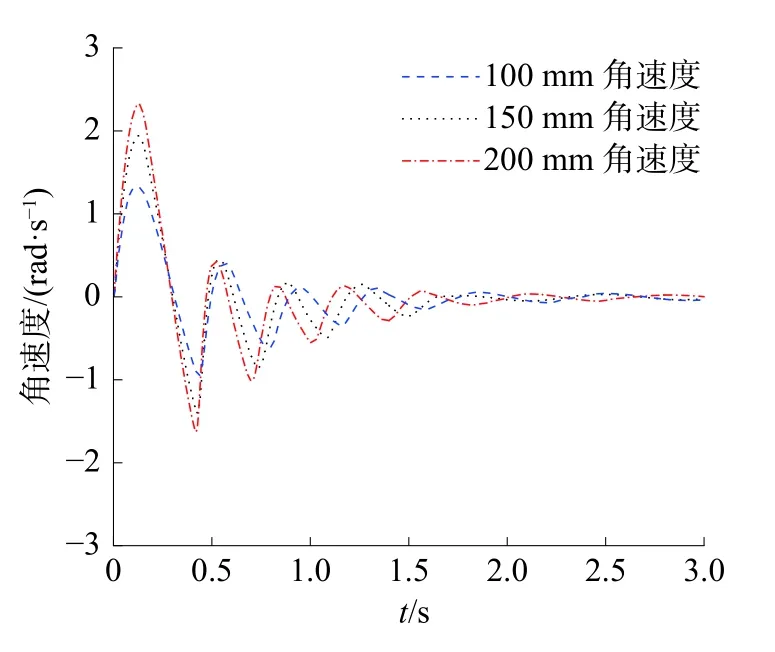
图7 挡板角速度

图8 挡板所受力、力矩

图9 为受力曲线峰值处挡板内表面压力云图。图9 中：第一峰值处压力大、受力面积大、压力云图梯度边缘稳定平滑；第二、第三峰值处压力较小、受力面较小、梯度边缘出现紊乱；第四峰值处所受力和受力面积均进一步减小。

图9 各峰值时刻挡板内表面总压力

4.3 最高液位变化分析

对挡板开启运动过程中水箱最高液位变化进行分析，将液相体积份额为0.95 等值面的最高点作为最高液位，得到数值模拟最高液位数据。液面变化的实验结果与模拟结果比对如图10 所示。由图10 可以看到总体趋势模拟结果与实验数据符合较好，说明VOF 方法适用于溃坝问题自由界面的模拟，本文模拟结果可信有效。在初始液位高度为100、150、200 mm 工况下，前期模拟值与实验值符合较好；在约0.5 s 后，模拟值开始与实验值产生些许偏差。

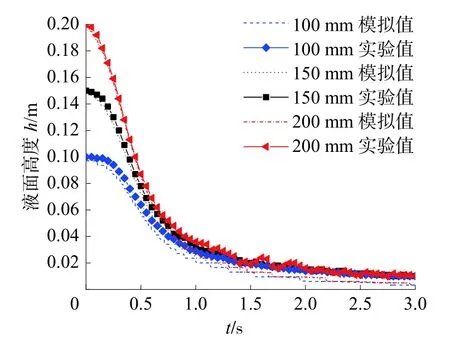
图10 3 种工况下液面高度实验值与模拟值

图10 模拟结果呈阶梯状，这可能是由于溃坝水流经挡板开口泄出形成的体积变化传导至最高液位变化过程较缓，响应较慢，无法形成较平滑的变化曲线；另一方面，由于求解区域网格化的影响，使最高液位变化曲线呈阶梯状分布。结合图4 网格敏感性分析结果，这说明VOF 方法对于时间响应较慢和自由界面捕捉情况下，对网格尺寸和时间步长要求较高，除非网格够细或时间步长够长，否则溃坝最高液面曲线无法平滑。

4.4 挡板开启角度变化分析

图11 对比了挡板开启角度实验结果与模拟结果，模拟结果反映了挡板运动角度变化趋势，与实验结果符合较好。

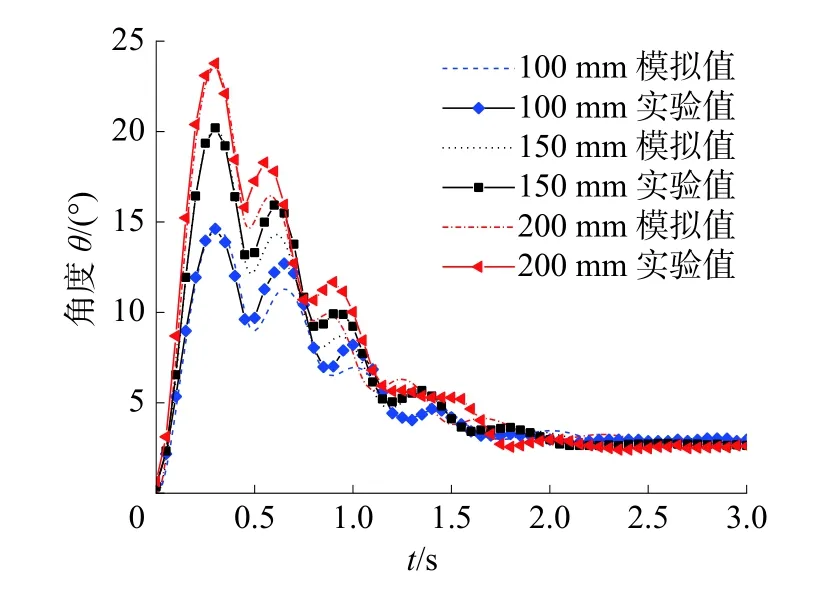
图11 3 种工况下开启角度实验值与模拟值

挡板受溃坝水流形成的射流冲击，其摆动呈现一定的规律性。如图12 所示，随初始液位的线性增加，挡板振动幅度呈递增态势，且递增幅度逐渐减小。这是因为初始最高液位逐渐接近挡板旋转轴，流体静压提供挡板的转矩并非满足线性递增关系。振荡周期越靠前，初始液位对振荡幅值的影响越小，幅值递增曲线越缓。

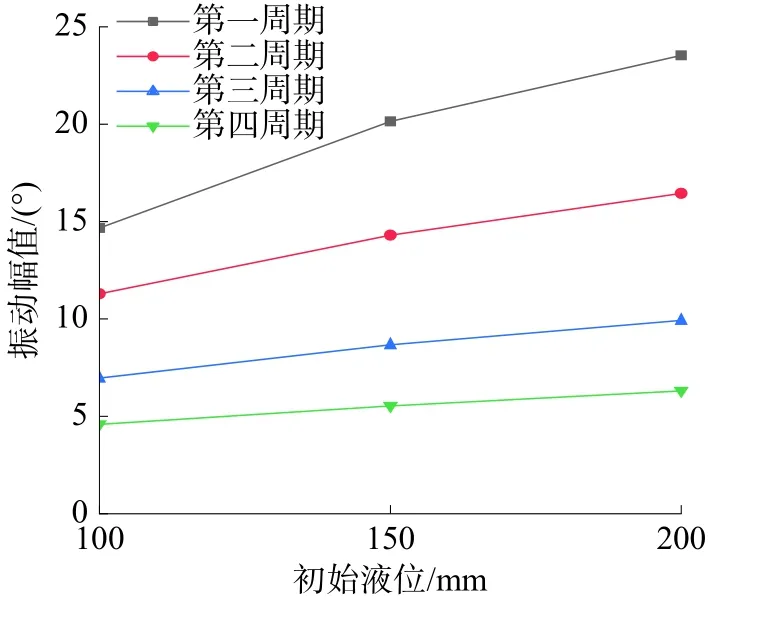
图12 各周期振动幅值

随初始液位的增加，周期时长呈递减趋势，如图13 所示。值得注意的是，第二、第三周期时长较为接近，但第四周期时长却远大于第二、第三周期。这是由于第四周期处于挡板运动末期，挡板所受动压较小，做功功率低，引起挡板运动状态变化需要更长时间。

图13 各周期时长

在初始液位递增条件下，振荡周期发生时间出现了明显时延现象，如图14 所示。振荡周期越靠前，时延现象越不明显，第一周期几乎不会随初始液位变化而时延。

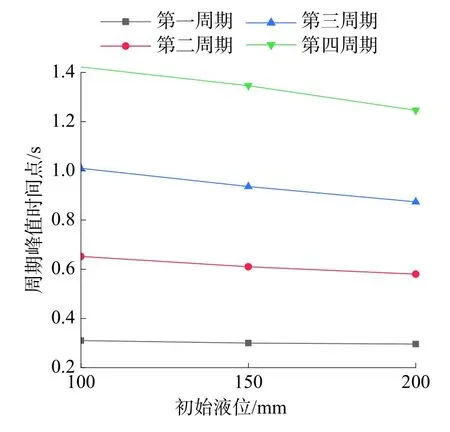
图14 各周期峰值时间点

与图10 中溃坝最高液位曲线一样，注意到初始液位100、150、200 mm 工况下，挡板摆角模拟值也均于约0.5 s 后开始偏离实验值。结合图11，偏差从挡板第一次回落受到射流冲击时刻开始，根据图9 压力云图峰值处出现压力梯度边缘不清晰现象，推测可能为VOF 模拟冲击射流界面不够精细导致DFBI 转矩计算产生偏差，说明VOF 结合DFBI 模型对于溃坝水流形成的冲击射流冲击刚体运动还有进一步提升空间。

5 结论

1)本文通过将模拟与实验结果对比，证明了VOF 方法结合DFBI 模型的CFD 数值模拟方法可以较精确地描述溃坝冲击问题，为今后使用该数值模拟方法求解类似问题提供了有力的实验依据。

2)溃坝挡板振荡呈现周期性。振荡幅度随着初始液位的增加而增加，且随初始液位增高，振荡幅值增加程度逐渐降低，周期时长逐渐减小，时延现象逐渐减轻。

3)使用VOF 方法模拟溃坝水流自由表面，在时间响应较长和界面捕捉方面对于网格尺寸要求较高，适当加密网格会对结果大大改善。

4)VOF 方法和DFBI 模型结合对溃坝水流形成的冲击射流冲击刚体运动还有一定提升空间。