天目山地区重污染天气预测模型及其环流特征研究

李 云， 张 莹， 许金萍， 蒋晓梅， 杨 聃， 梁明珠

(1.浙江省安吉县气象局,浙江 安吉 313300； 2.浙江省湖州市气象局,浙江 湖州 313000)

引 言

在全国污染物减排的大背景下，气象条件显然已成为大气污染浓度变化的最重要因子[1-7]。包括地面气象观测要素及天气形势场及其相关物理量在内的气象条件，是研究地区大气重污染事件的主要对象。然而污染物浓度变化的主要驱动因子不同研究区域之间有较大的差别。Zhang等[8]研究发现，环流形势是北京地区污染物浓度逐日变化的主要驱动因子。杨茜等[9]探究了降水对重庆市大气污染物浓度的影响，发现PM2.5、PM10浓度随降水量增加逐渐降低，降低趋势线较为明显。马格等[10]对郑州市气象因子对大气颗粒物浓度的影响研究发现，降水、风向、湿度与大气颗粒物浓度相关。刘雯等[11]对武汉市观象台2013—2016年PM2.5质量浓度变化及其与气象因子的相关分析发现，PM2.5质量浓度变化与降水量、风速和气温等气象因子明显相关。王景云等[12]分析了2012—2015年北京市空气质量指数变化及其与气象要素的关系，发现整体上空气质量指数与风速、日照时数、降水量、平均气温和最高气温呈负相关，与湿度呈正相关。李德平[13]、孙燕[14]等通过分析发现，风是重污染的主要因子之一。刘郁珏等[15]对北京市房山区大气污染物时空分布特征及气象影响因素分析发现，在不同季节条件下，局地气象要素与污染天气发生概率之间有着很好的相关关系；Pearce等[16-17]研究也指出，局地气象条件而非天气形势是污染物日变化的主要驱动因子。大气污染物浓度的变化与多个非独立因子的气象条件有着非线性关系。何建军等[18]利用ANN技术，构建了气象条件、污染物排放变化和污染物浓度的预测模型，其对NO2模拟准确度最好，其次是SO2的模拟，对PM10的模拟结果最差。宋丹等[19]通过多元线性逐步回归和BP神经网络方法，分季节建立空气质量指数预报模型，夏季指数准确率近99%，冬季超过或接近80%。

为构建一个较高准确度的重污染天气时PM10及PM2.5最优预测模型及其气象条件特征，本文以浙江天目山为例开展研究。

天目山地区位于浙江西北部，西接皖南，经浙、皖边境过杭嘉湖平原西缘，呈西南—东北走向。山脉主体在安吉、临安境内，余脉还延伸至德清、余杭境内。由于浙江省内的重污染天气西部比东部的多，持续时间长，北部又比南部的多，加之天目山山脉影响，致使天目山地区成了省内冬、春空气污染的重灾区之一。由于地处天目山山脉的安吉和临安，都是国家级生态建设示范区，因此本文重点探讨天目山地区重污染时期气象条件与污染浓度预测模型及其气象条件特征。

天目山地区空气污染监测数据时间序列普遍偏短，重污染天气数量少。李云等[20]研究发现，安吉地区大气颗粒物浓度及气象要素数据的多元线性回归方程拟合度差，与显著性要素偏少有密切关系。

据有关研究和大量的使用结果显示，支持向量机(SVM)[21-24]是一种优秀的浅层学习方法，在小样本训练集上有着无可比拟的优势，能够得到比其他算法好很多的结果。LIBSVM是台湾大学林智仁教授开发设计的一个快速有效的SVM模式识别与回归方法。因此本文尝试使用支持向量机(LIBSVM)方法，以期解决重污染时期气象条件与污染浓度预测模型精确度问题。

1 研究方法

在针对2015年1月—2018年10月天目山地区出现的重污染天气(AQI大于等于151)，分别建立PM2.5、PM10日数据最优预测模型，并对其环流特征进行分析。

1.1 基于LIBSVM最优预测模型构建

择优选取天目山地区8个大气成分监测站，以及安吉、临安、德清及余杭气象国家站小时数据，对天目山地区地面气象观测要素(包括雨量、气温、最高气温、最低气温、本站气压、海平面气压、湿静力能量、最大风速、极大风速、露点温度、温度露点差、水汽压、相对湿度、最小湿度、能见度、最小能见度、地面温度、地面最低温度)、NECP再分析(FNL)资料(包括30°-31°E、120°-121°N的1000、850、700、500 hPa形势场及边界层高度、最大纬向风、最大经向风、2 m温度、地表温度等相关物理场)及对应的PM2.5、PM10浓度进行数据预处理和日数据统计，利用LIBSVM方法,对PM2.5、PM10分别建立预测模型及参数(主要是惩罚参数c和核函数g)寻优。

建立基于LIBSVM方法预测模型及参数寻优，首先对PM2.5、PM10、地面气象要素、FNL再分析资料分别归一化处理，然后进行PCA降维，最后用交叉验证(CV)、粒子群优化(PSO)和遗传(GA)等算法分别进行预测模型参数对比寻优。

1.2 最优预测模型c和g参数寻优

关于SVM参数的优化选取，国际上没有公认的统一方法，目前常用的是利用K-CV算法进行交叉验证[25]。

K-fold Cross Validation(K-CV)是常见的CV方法之一。它将原始数据分成K组，将每个子集数据分别作一次验证集，其余的K-1组子集数据作为训练集，这样会得到K个模型，将K个模型最终的验证集的分类准确率的平均数作为此K-CV下分类器的性能指标。K-CV可以有效地避免过学习及欠学习状态的发生，最后得到的结果比较具有说服性。

K-CV算法需要遍历网格内所有参数点参数寻优，相对费时。PSO和GA等启发式算法的参数寻优可更快找到最优解。GA是一种基于生物遗传和进化机制的适合复杂系统优化的自适应概率优化技术，也是一种实用、高效、鲁棒性强的优化算法。PSO是一种基于群体智能的演化算法，通过粒子在解空间追随最优的例子进行搜索。

1.3 对应最优环流形势场及物理量指标特征分析

利用构建PM2.5、PM10最优预测模型的地面气象观测要素、FNL再分析资料结果，对参与最优预测模型的环流形势场及相关物理量进行k-means聚类分析，根据相关研究和本地经验选取k=4、5、6进行对比择优；根据择优结果，将相同类型的环流形势场进行合成计算，得到重污染天气PM2.5、PM10对应的最优环流形势场，并分析重污染天气环流特征。

2 结果分析

2.1 重污染天气下PM2.5日数据最优预测模型及参数寻优

根据与PM2.5的相关系数的绝对值与显著性特点，将55个气象条件按照顺序进入模型参与预测，在训练值占比69%，相关性与显著性最好的27个要素参与时得到了重污染天气下PM2.5日数据最优预测模型(表1)。由表1可知，最佳c为2.7114，g为3.6141，训练值和测试值的R2分别达到了0.9992和0.7196。对比分析预测值与初始值发现(图1)，不仅训练值与趋势都很好吻合，测试值也取得了很好的检验结果。因此本文构建的模型考虑要素合理，方法合适，取得了很好的预报效果。

表1 PM2.5最优预测模型参数寻优

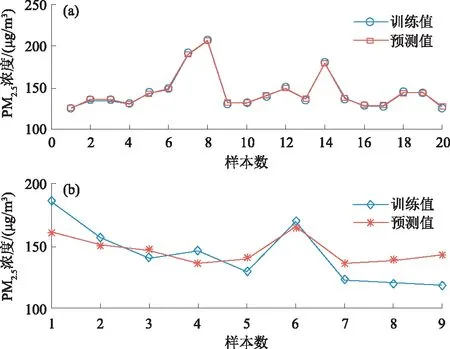
图1 基于支持向量机的训练集(a)和测试集(b)PM2.5最优预测模型

2.2 重污染天气下PM10日数据最优预测模型及参数寻优

与PM2.5一样的方法与步骤，在训练值占比69%，相关性与显著性最好的24个要素参与时得到了重污染天气下PM10日数据最优预测模型(表2)。由表2可看出，最佳c=30.3874，g=1.6613，训练值和测试值的R2分别达到了0.9978和0.7792。对比分析预测值与初始值发现(图2)，不仅训练值与趋势都较好吻合，虽然测试值的趋势不如PM2.5的好，但明显优于何建军等[18]得到的R值0.67(R2值0.4489)。因此本文构建的模型考虑要素合理，方法合适，取得了更好的预报效果。

图2 基于支持向量机的训练集(a)和测试集(b)PM10最优预测模型

表2 PM10最优预测模型参数寻优

2.3 对应最优环流形势场特征分析

聚类有效性的评价标准有两种：一是外部标准，通过测量聚类结果和参考标准的一致性来评价聚类结果的优良；另一种是内部指标，用于评价同一聚类算法在不同聚类数条件下聚类结果的优良程度，通常用来确定数据集的最佳聚类数。

最佳聚类数判定的方法，对于内部指标，通常分为三种类型：基于数据集模糊划分的指标，基于数据集样本几何结构的指标，基于数据集统计信息的指标。基于数据集样本几何结构的指标根据数据集本身和聚类结果的统计特征对聚类结果进行评估，并根据聚类结果的优劣选取最佳聚类数。本文主要介绍Calinski-Harabasz(CH)指标、Davies-Bouldin(DB)指标和silhouette(SI)指标。

(1)CH指标

CH指标通过类内离差矩阵描述紧密度、类间离差矩阵描述分离度，指标定义为

(1)

其中，n表示聚类的数目,k表示当前的类,trB(k)表示类间离差矩阵的迹,trW(k)表示类内离差矩阵的迹。CH越大,代表着类自身越紧密，类与类之间越分散，即更优的聚类结果。

(2)DB指标

DB指标描述样本的类内散度与各聚类中心的间距，定义为

(2)

其中，K是聚类数目，Wi表示类Ci中的所有样本到其聚类中心的平均距离，Wj表示类Ci中的所有样本到类Cj中心的平均距离，Cij表示类Ci和Cj中心之间的距离。可以看出，DB越小,表示类与类之间的相似度越低，从而对应越佳的聚类结果。

(3)SI指标

对于D中的每个对象o,计算o与o所属的簇内其他对象之间的平均距离a(o):

(3)

b(o)是o到不包含o的所有簇的最小平均距离

(4)

轮廓系数定义为

(5)

Si越接近1，则说明样本i聚类越合理。

2.3.1 PM2.5环流形势场分类

利用构建PM2.5最优预测模型的地面气象观测

要素、FNL再分析资料，对参与最优预测模型的环流形势场及相关物理量进行k-means聚类分析。根据相关研究和本地经验选取k=4、5、6进行对比择优[26],其中k=5时,DB指标、SI指标最优，CH指标次优。YC最优污染天气环流类型分5类(表3)，第四类最多，第五类次之，第二、三类最少。其中第一类5天，占17.2%；第二类、第三类各2天，各占6.9%；第四类11天，占37.9%；第五类9天，占31.0%(表略)。

表3 PM2.5和PM10不同k值聚类有效性指标比较

2.3.2 PM2.5环流特征

利用k-means聚类方法，最优归类出5类，根据相关性较好的700 hPa合成环流形势分别是第1类弱脊型(图3a),第2类低槽南压型(图3b),第3类浅槽东移型(图3c),第4、5类均属于高压脊控制(影响)型(图3d和3e)，而第4类的脊线更密，脊区更深厚。

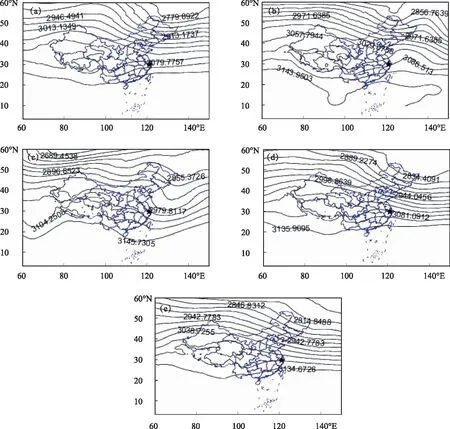
图3 第1—5类700 hPa合成环流形势(a)为第1类弱脊型，(b)为第2类低槽南压型，(c)为第3类浅槽东移型，(d)(e)为第4、5类高压脊控制(影响)型；图中★指天目山地区

第2、3类天目山地区分别属于槽前、槽后天气，是5种类型中最少的一类，第2类容易出现降水，污染持续时间较短；第3类气温低,露点低，湿静力能量小，大气边界层高度较低，不利于污染扩散；第1类弱脊型，湿度大，温度露点差小，容易出现降水，不利于污染持续；第4、5类均属于高压脊控制(影响)型，天目山地区处在西北或偏西气流控制，容易出现长时间持续污染，是天目山地区影响PM2.5浓度的最主要天气类型。

2.3.3 PM10环流形势场分类

对参与最优预测模型的环流形势场及相关物理量进行k-means聚类分析，根据相关研究和本地经验，选取k=4、5、6进行对比择优。其中k=6时，DB指标、CH指标最优。因此最优污染天气环流类型分5类(表3)，第1类最多，第2、3类次之，第6类最少。其中第1类9天，占31.0%；第2类、第3类各6天，各占20.7%；第4类5天，占17.2%；第5类、第6类分别为2天、1天，合计10.3%(表略)。

2.3.4 PM10环流特征

利用k-means聚类方法最优归类出的6类，根据相关性较好的700 hPa环流进行分析，对应500 hPa合成环流形势分别是第1、3、4类均属于高压脊控制(影响)型(图4a、4c和4d)，而第4类的脊区更深厚、宽广；第2类为低槽南压型(图4b)；第5类低涡东移型(图4e)；第6类低涡南压型(图4f)。

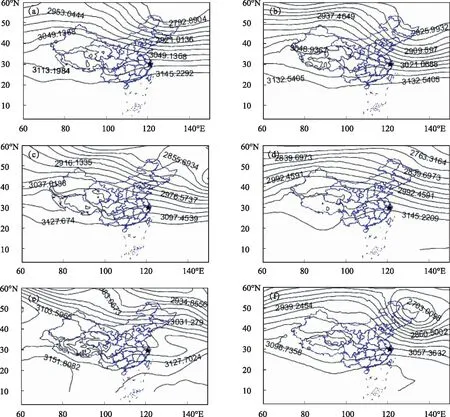
图4 6类700 hPa合成环流形势(b)为第2类低槽南压型，(e)为第5类低涡东移型，(f)为第6类低涡南压型，(a)(c)(d)为第1、3、4类高压脊控制(影响)型；图中★指天目山地区

第5、6类天目山地区分别属于槽(涡)后天气，是6种类型中最少的两类，容易出现降水，污染持续时间较短；第2类气温低，露点低，湿静力能量较小，大气边界层高度较低，不利于污染扩散；第1、3、4类均属于高压脊控制(影响)型，天目山地区处在西北或偏西气流控制，容易出现长时间持续污染，是天目山地区影响PM10浓度的最主要天气类型。

3 结 论

针对2015年1月-2018年10月天目山地区出现重污染天气(AQI大于等于151)，建立基于LIBSVM方法的预测模型及参数寻优；对参与最优预测模型的环流形势场及相关物理量进行k-means聚类分析，得到重污染天气PM2.5、PM10对应最优环流形势场并分析重污染天气环流特征，得到如下结论。

(1)根据与PM2.5的相关系数的绝对值及显著性特点，将55个气象条件按照顺序进入模型参与预测，在训练值占比69%，相关性与显著性最好的27个要素参与时得到了重污染天气下PM2.5日数据最优预测模型，训练值和测试值的R2分别达到了0.9992和0.7196，训练值与趋势都能很好吻合，测试值也取得了很好的检验结果。因此本文构建的模型考虑要素合理，方法合适，取得了很好的预报效果。

(2)由相关性与显著性最好的24个要素参与，得到了重污染天气下PM10日数据最优预测模型，虽然测试值的趋势不如PM2.5的好，训练值和测试值的R2分别达到了0.9978和0.7792，训练值与趋势吻合较好。因此本文构建的PM10模型考虑要素合理，方法合适，也取得了更好的预报效果。

(3)PM2.5最优预测模型对应最优5类700 hPa合成环流形势中第4、5类均属于高压脊控制(影响)型，容易出现长时间持续污染，是天目山地区影响PM2.5浓度的最主要天气类型。PM10最优预测模型对应最优6类700 hPa合成环流形势中第1、3、4类均属于高压脊控制(影响)型，容易出现长时间持续污染，是天目山地区影响PM10污染的最主要天气类型。

虽然构建的天目山重污染天气预测模型取得了较好的预报效果，但缺少要素个数、训练与测试比率等对预测模型影响因子的量化分析，对预测模型的稳定和推广有较大的制约。另外，研究更小尺度，如1 h、3 h等，以及非重污染天气的预报模型和构建无缝预报体系是今后研究重点之一。