基于故障树的军机复杂系统任务可靠性建模预计方法研究

刘世华，黄轶华，邹 蕊，阿西达

（航空工业洪都，江西 南昌，330024）

0 引言

任务可靠性预计是估计产品在执行任务过程中完成其规定功能的概率。目前军机系统级任务可靠性预计常见形式为绘制任务可靠性框图，通过串联、并联、表决和旁联等数学模型进行计算。随着军机系统复杂性的提高，关键系统具备功能重构设计，余度设计，系统内部的交联关系更加复杂，系统之间接口关系复杂，使得此种传统预计方法已不能保证对于复杂系统可靠性预计的完整性、精确性及与系统设计的一致性要求。因此，本文以某型机航电系统为例，建立以顶层任务失败为顶事件，以单元的输入端口功能失效状态和单元自身的失效状态为底事件的故障树，以形式化建模语言Altarica为核心，实现接口、输入端口、输出端口失效的故障树拼接，建立与系统设计一致的形式化模型，通过Saftylab、Rellab等常用软件在此基础上实现自动化的故障树生成并计算系统任务可靠性指标。

1 任务可靠性建模方法

按照系统在执行任务剖面中的具体任务，梳理系统顶层功能及各功能对任务阶段的影响，明确系统任务失败判据，即在各任务阶段，哪些功能发生故障会对任务阶段产生影响，进而影响整个任务的完成。通过对系统功能建模和故障逻辑建模，建立以顶层任务失败为顶事件，以单元的输入端口功能失效状态和单元自身的失效状态为底事件的故障树模型。

2 系统故障建模

2.1 系统功能建模

2.1.1 系统故障判据建模

系统故障判据建模，是以系统顶层功能的故障模式为底事件，以任务阶段失败为顶事件，建立故障树，确定任务阶段失败与系统顶层功能故障模式之间的逻辑关系，得到系统任务失败判据。

以某型机训练剖面中“地面试车后起飞滑跑”阶段为例，相关功能为飞机航姿感知功能、飞行高度感知功能、侧滑角感知功能、位置导航功能等19个二级功能组成，组合逻辑为任一功能失效，则该任务阶段失败。“地面试车后起飞滑跑”任务阶段失败判据建模见图1。

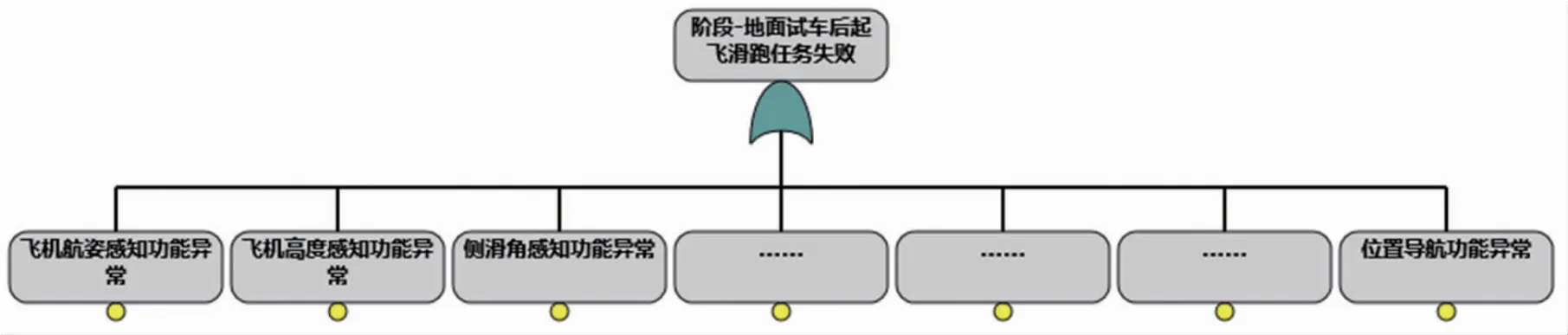
图1 “地面试车后起飞滑跑”任务阶段失败判据建模

2.1.2 系统顶层功能建模

航电系统最终输出的端口包括显示功能、数据采集记录功能、通信功能、攻角指示功能、武器外挂功能、训练功能、照明功能、控制功能、飞行信息感知功能、导航等。功能模型如图2所示。

图2 航电系统顶层功能模型

2.1.3 系统内部构架建模

航电系统由显示控制管理子系统、武器外挂子系统、通信导航子系统、大气数据子系统、惯导子系统等9个子系统组成，根据系统功能原理，构建系统内部功能模型，由于航电系统内部功能模型较大，无法全部展示，仅以惯性导航子系统为例，根据惯性导航子系统所含模块创建内部结构，根据系统功能流图创建功能交联关系。惯性导航子系统功能模型见图3。

图3 惯性导航子系统功能模型

2.2 故障逻辑建模

2.2.1 功能失效状态定义

在功能模型中，系统或单元的每个输出端口都代表一个系统或单元的功能，称为“功能端口”，功能端口的类型中，就定义了这个功能的所有故障模式。这里以“导航功能”为例，示例功能失效状态定义，如图4所示。

2.2.2 单元失效状态定义

在功能模型中，除了功能端口的失效定义外，还有单元的失效状态定义。单元的失效状态是指单元自身的功能故障模式，这些故障模式可能会影响到单元输出功能的状态。图5是惯性导航部件的单元失效状态定义。

2.2.3 故障逻辑建模

故障逻辑建模就是以单元的输出端口功能失效状态为顶事件，以单元的输入端口功能失效状态和单元自身的失效状态为底事件，建立故障树，描述它们之间的逻辑关系，如图6所示。

图6 某单元故障逻辑建模示例

3 任务可靠性预计

在系统功能建模和所有单元的故障逻辑建模完成后，整个系统的故障建模就完成了，通过Saftylab、Rellab等软件自动生成以顶层任务失败为顶事件，以单元的输入端口功能失效状态和单元自身的失效状态为底事件的故障树模型，由系统内各成品失效率自底向上计算顶事件发生概率，然后基于故障树进行最小割集分析及任务可靠性指标预计。

4 应用实例

以航电系统为例，运用上述方法构建先以系统顶层功能的故障模式为底事件，以任务阶段失败为顶事件的故障树，再以单元的输出端口功能失效状态为底事件，以系统顶层功能的故障模式为顶事件的故障树，最后以单元的输入端口功能失效状态和单元自身的失效状态为底事件，单元的输出端口功能失效状态为顶事件的故障树。通过将此三层故障树拼接，建立与系统设计一致的形式化模型，由系统内各成品组成及各成品失效率，得到航电系统训练剖面任务失败为顶事件的故障树的最小割集及任务可靠性指标，如图7和图8所示。

图7 航电系统任务可靠性分析结果

图8 航电系统任务可靠性预计结果

5 结语

本文通过以某型机航电系统训练任务失败为顶事件，以单元的输入端口功能失效状态和单元自身的失效状态为底事件构建故障树，以形式化建模语言Altarica为核心，建立与系统设计一致的形式化模型，通过Saftylab、Rellab等评估软件在此基础上实现自动化的故障树生成并且对任务可靠性给出定量和定性分析，弥补了传统预计方法的不足，可保证复杂系统可靠性预计的完整性、精确性及与系统设计的一致性要求，使得复杂系统任务可靠性预计结果更准确。