基于网络可控性的地铁客流控制站点识别研究

吴开信，吴子航，冯家汇

（1.五邑大学 轨道交通学院，广东 江门 529020；2.深圳地铁运营集团有限公司，广东 深圳 518040）

地铁在优化城市空间布局、缓解道路交通拥堵、改变居民出行方式等方面发挥了重要的作用，已成为城市居民出行的首选，但在北上广深等一线城市早晚高峰期，地铁有限的运输能力与迅猛增长的客流需求之间的矛盾日渐突出，给车站运营和乘客安全带来了严重挑战.对部分站点实施客流控制，使其服务水平保持在合理的范围之内是城轨系统高峰期采取的常见措施之一.控流方案的制定主要是基于对客流时空特征的分析，从单个站点[1-2]、整条线路[3-4]、关联网络[5-6]等角度对站点选择、控流时间、控流强度等指标进行优化，这种采取优化模型的方法在遇到大规模问题时，需要以较大的计算代价来获得问题的满意解，其控流效果有待提升.

地铁运营线路和客流加载过程可用赋权的复杂网络描述，而目前网络科学与工程的研究对象集中于随机网络、小世界网络和无标度网络，多基于网络拓扑结构对网络的脆弱性、鲁棒性、可靠性等结构特性进行研究，将控制理论与网络科学相结合的研究起步较晚，且其中的控制策略也由传统控制理论中的蜂拥控制转到现在的牵制控制[7].Kalman[8]指出，一个动态系统只需找到合适的驱动节点集并加以控制，就能从初始状态到达任意理想状态.Liu等[9-10]首次将线性时不变系统的可控性应用于网络控制，并提出复杂网络控制中心分布取决于网络的度分布.Meng[11]基于改进的LB模型研究了铁路列车服务网络在出现应急情况下的可控性问题，但对网络节点和边权等属性特征的探讨不够深入.综上，既有文献大多是基于复杂网络的物理结构、侧重于网络特性指标分析，从系统可控性角度提出网络控制方法和应对策略并应用于实际的文献较少；另外，既有研究的网络多数是静态网络，对节点之间的交互作用和时效特征等缺乏考虑.选择合适的站点进行客流控制有利于提高城轨系统高峰期客流时空分布均衡度和运力资源的有效利用率，本文基于网络可控性原理采取定量分析方法，从有向网络结构特性分析入手，综合考虑各车站客流状态及其动态变化过程，以有效识别客流控制站点的个数与具体站点.

1 模型的构建

1.1 有向客流网络的动力学建模

根据地铁物理网络拓扑结构以及客流特性，构建有向网络图G=（V,E），图中节点集V=｛v1,v2,…,vi,…,vj,…,vN｝对应于车站集 ｛1,2,…,i,…,j,…,N｝，如果从车站i去往车站j存在客流量，则连接一条有向弧E（vi,vj）.定义网络中几个指标：节点vi的度是0-1变量，当nij=1时，表示E（vi,vj）存在，否则表示不存在；度的值反映了网络节点之间的可达性，值越大说明乘客有更多的出行路径选择.网络平均路径长度表示i站和j站之间的最短路径距离，L反映了从车站i去往车站j平均经过的车站数，是网络连通性的一个指标.pij（t）分别表示t时刻i站的进站乘客数、出站乘客数以及从i站去往j站的乘客数.由于高峰期常态大客流通常以通勤通学为目的，乘客起讫点相对固定，的值可由AFC实时数据统计分析获得，设为常数.考虑地铁对居民职住地选择和通勤出行行为的影响，本文利用在路网规划中常用的基于旅客空间相互作用的重力模型对pij（t）进行估计，即：

大多数复杂网络虽然具有非线性特征，但是在结构上与线性系统有相似性质[9].假设对限流的时间段进行细分，在一个充分小的Δt时间段内，系统参数不随时间的变化而变化，则客流网络系统可用线性时不变动力系统微分方程表示为：

模型具有线性和时不变性两个特征，向量x（t）=（x1（t）,x2（t）,…,xN（t））T表示t时刻网络内各车站的客流状态，xi（t）可看作车站i实际客流强度；A=（aij（t） ）N×N为基于网络拓扑结构的客流转移矩阵，其中aij（t）≠ 0 表示网络图中存在从节点vj指向节点vi的边，其值表示站间的客流转移情况；式（2）刻画了Δt时间段内客流变化过程.

在［t,t+Δt］区间内，若存在一个分段连续的输入u（t），使系统由初始状态x（t）转移到期望状态x（t+Δt），则称系统在此状态是可控的.若所有状态皆可控，则称系统可控.高峰时段的客流分布和运能之间通常不匹配，若以外界实施的控流措施作为输入条件，则控流效果可表示为：

其中，输入矩阵B=（bij（t） ）N×M表示t时刻被选择进行客流控制的M（M≤N）个车站；输入信号u（t）=若t时刻j站限流，则取b（t）=1 （i=j），否则为0；u（t）为j ijj站的控流强度.

1.2 客流网络可控性分析

在有向网络中，带有控制输入的节点为控制节点，只有单一输入的控制节点为驱动节点，如果从控制节点到状态节点至少存在一条链，则称此状态节点为被控节点.系统可控情形下，输入信号可通过某条路径到达所有的节点.基于系统可控性优化主要解决两个问题：最少需要多少驱动节点数Nd使系统可控；如何进行驱动节点的选择以使控制效果更好.

文献[8]提出，线性系统完全可控的充分必要条件是由A和B构成的 Kalman判别矩阵c的行秩是满秩，即满足：

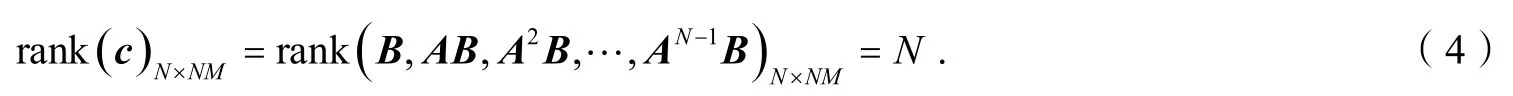
以图1的网络为例，在图1-a中：

图1 有向网络可控性判别

此时rank（c）=4，网络可控.而图1-b中 rank（c）=3＜4，网络处于不可控状态.

文献[9]提出了网络可控性与最大匹配相关联的最小输入理论，即控制一个有向网络所需的最少输入数量(驱动节点数)等于二分图的最大匹配中未匹配节点数量.若存在完全匹配，则最少驱动点Nd=1；如果不存在完全匹配，则Nd为网络最大匹配集所对应的未匹配节点的个数.

本文将地铁客流控制站点的识别问题转化为：如何从网络中找出有限个驱动节点，使不可控网络转化为可控网络.基于以上分析，可采取如下思路：将图G（V,E）转化为二分图，节点vi分为由此构成两个不同的节点集边集E=设M为二分图边集的一个子集，若M中的任意两条边都没有公共的起点和终点，则称M是一个匹配，如果一个节点是M中的一条边的终点，则该节点就是匹配节点，否则为非匹配节点，非匹配节点即为驱动节点.网络的所有边没有共享的头节点或尾节点时，网络达到最大匹配.图2给出了图1-b所示网络到二分图之间的映射关系，根据最大匹配原理求得非匹配节点为｛v1,v4｝.对非匹配节点（驱动节点）给予相同数量的输入信号，可实现对整个网络的有效控制.

图2 网络到二分图的映射关系

从示例可以看出，系统可控与否主要取决于其拓扑结构和外界输入条件，但在实践运用中会遇到以下问题：1）对于简单有向网络，可以利用枚举法通过不断添加和判断两个过程寻找最少控制点，计算其复杂度为2N-1，对于大型网络此方法在理论上可行，实际却不可行；2）由于客流是动态变化的，aij（t）的实时数据具有滞后性，只能取得近似值.针对以上两种情形，本文进一步提出优化算法.

2 基于最小驱动点集的控流车站识别优化方法

由于在地铁网络高峰期，不同线路、同一线路的上下行方向以及线路各断面之间会存在客流空间分布不均衡现象；另外由前面分析可知，客流的实时精确数据难以获得.为了解决问题的主要矛盾，针对有向弧上的流量引入阈值q0，基于q0对初始网络矩阵中的有向弧进行删减，当pij≥q0时，取aij（t）=pij（t），保留弧E（vi,vj）；当pij（t）＜q0时，取aij（t）=0，剔除弧E（vi,vj），将初始网络转化为骨干网络.

当r ank （c）=ra nk （B,AB,A2B,…,AN-1B） ＜N时，说明系 统处 于不可 控状 态，此 时添 加新的 虚 拟输入节点vk，连接有向弧E（vi,vk），新系统的输入-输出模型可定义为：

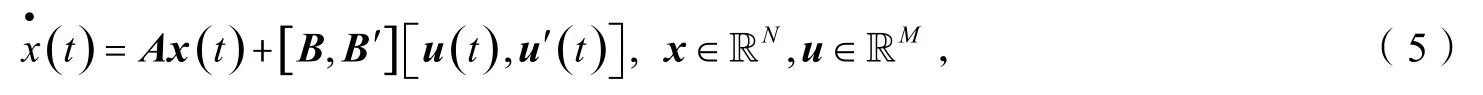
其中B'=（Ek），Ek为单位矩阵的第k列的列向量，u'（t）为新增的输入信号.令 r ank （c'）=rank([B,B'],A[B,B'],A2[B,B'],…,AN-1[B,B'])，称f（i）=ra nk(c')-r ank（c）为节点vi的控制能力.若f（i）≠ 0，则称节点vk的添加为节点vi的有效添加，否则为无效添加.遍历vk的所有有效添加的节点，称max{f(i)i=1,2,…,N}对应的连接为节点vk的最优连接.

具体算法如下：

步骤1：构造骨干网络矩阵A.

步骤2：对化简后的骨干网络求最小驱动点集.

1）初始化，令S=0,U=[ ],b=[ ],v={}.计算节点vi（i=1,2,…,N）的控制能力f（i），按值的降序对节点进行排列.

2）添加新的输入节点vk，按下列规则寻找最优连接：若vk是关于某节点的无效添加，则考虑下一个点，直至找到所有有效添加节点集合，选择vk的最优连接E（vi,vk）.此时有：S=vi,U=

3）循环，直到所有添加的输入节点都找到最优连接.

4）终止条件：判别矩阵行秩为满秩.

高峰期客流控制时间设为[0,T]，将其等分成长度为δ的个小时间段，满足=T.在每个δ时间段内，依据本文提出的算法对控制站点进行识别，重复上述过程，可得出整个高峰时段的最优控流策略.由于车站客流强度是时间的函数，因此，控流车站的选择在实施过程中也是一个动态的过程.

3 算例实验

深圳地铁目前已运营线路共设有283座车站，为减少问题复杂度，本文以客运量较大的3号线为例.3号线全长42 km，共30座车站，采用6节编组的B型地铁列车，早晚高峰期列车追踪间隔时间已缩减至150 s，区间最高运营速度85 km/h.某4个连续工作日18:30到18:45实测15 min断面客流分布如图3所示，沿线潮汐客流特征明显，小时客流不均衡系数和区间断面客流不均衡系数皆较大，其下行方向部分区间拥挤度峰值高达121%.

图3 晚高峰断面客流分布

根据换乘节点所通过线路的条数，针对所有换乘节点，添加相应个数相关联的虚拟节点，以表示线网间存在的客流转换关系.基于沿线各站进出的平均数据及站间距离，依据式（1）估计出晚高峰15min内客流OD数据，可得状态矩阵：

取车站日均客流量15 min内的平均值为阈值(q0=0.0213)，算得骨干矩阵为：

根据Kalman可控性判别条件可知系统处于不可控状态，主要原因在于：当q0的值逐渐增大时，骨干网络中有向弧逐渐减少，许多点会变成孤立点，对应的驱动节点数也将随之增多；其次，该线路有11个换乘节点，由最大匹配理论可知，换乘节点周围的不匹配节点较多，所需驱动节点的数量不够.

根据本文提出的搜索算法，当添加的输入节点达到7个及以上时，系统处于可控状态，此时限流车站达到 23%以上，路网在可控状态下的最优连接，即最小控流车站集合为{莲花村、老街、晒布、翠竹、田贝、布吉、六约}，这与该线路目前常态化限流车站的站点数量和实际站点基本吻合.

4 结论

本文结合图论和系统可控性原理研究了地铁高峰期客流控制站点的选择问题，给出了网络可控与否的判别方法，针对不可控情形，基于节点的控制能力提出最小驱动节点集合的搜索算法，算例验证了算法的合理性和有效性.

本文对客流控制只作了宏观方面的研究，具体的控流强度和控流措施没有涉及；在将原始客流网络转化为骨干网络时，阈值的选取也带有一定的主观性；另外，驱动节点数目与节点的度分布之间的关系值得进一步探讨.这三个方面在今后的地铁客流控制量化分析中再作深入研究.