基于遗传算法的非球面眼镜片设计

李念宁，项华中，高健东，张 露，郑 刚,4，陈家璧，王 成,4，张大伟,3，庄松林,3

（1.上海理工大学 医疗器械与食品学院 生物医学光学与视光学研究所，上海 200093；2.上海理工大学 教育部光学仪器与系统工程研究中心，上海 200093；3.上海理工大学 光电信息与计算机工程学院，上海 200093；4.上海理工大学 上海市介入医疗器械工程研究中心，上海 200093）

引 言

眼镜是用于矫正屈光不正的光学器件，通过改变入射光线的聚散度使像成于视网膜上。设计眼镜片时，可以将镜片和人眼的组合视为一个光学系统，人眼的瞳孔直径约3～8 mm，眼球的水平视场可达120°，垂直视场可达80°，常用视场范围为0°～30°。因此这是一个小孔径、大视场的光学系统，可以忽略球差和彗差[1-2]，像散和畸变作为两种视场相关性像差是影响人眼视觉的主要因素。畸变不会影响像的清晰度，但当配戴者使用镜片周边区域视物时会感到不适，甚至眩晕[3-4]。球面透镜的中心光度准确，可以较好地矫正人眼屈光问题，但是其周边区域的像差较大，且镜片边缘较厚，而非球面镜片可以改善这些缺陷[5]。

引入非球面可以改善眼镜片的光学性能，因为非球面本身存在的像散可以与系统的像散抵消。非球面眼镜片的设计基于几何光学的基本原理，根据光线追迹可以计算出镜片的像散和畸变。选择合适的结构参数来降低这两种像差是设计过程中的重点。在前人的研究中，阻尼最小二乘法（DLS）是光学设计中最常用的优化算法[6]，该算法简单易行，在许多领域有着广泛应用，但是这种算法也存在容易陷入最小值、运算速度慢、依赖初始结构的选择等缺点。遗传算法可以解决这些问题[7-8]。Yen和Jin[9]将遗传算法与商业光学设计软件相结合，设计出了可减小人眼像差的人工晶状体；Yen和Ye[10]在设计接触镜时将遗传算法与神经网络相结合，提升了镜片的球差、彗差和调制传递函数（MTF），使配戴者戴镜时更舒适；唐运海等[11]将遗传算法用于渐进多焦镜子午线的优化设计，并采用加工测试的方法验证了算法的可靠性。虽然遗传算法在设计眼用设备方面已有许多应用，但是目前还没有用于设计单光眼镜片的研究。

本文从理论角度优化了前弯和非球面系数以平衡像差和畸变，再根据设计结果对镜片进行仿真和加工，并测量出镜片的光度分布情况和边缘厚度。对比测试结果与设计结果，得到最佳的结构参数。设计过程主要分为两步：首先将前弯和后表面非球面系数p同时作为自变量，用遗传算法优化得到像差较小时对应的参数，根据毛坯库存等实际生产情况，确定镜片前弯；接着将镜片后表面非球面系数p再次作为变量，寻找该前弯下像差和畸变最小时对应的p。本文主要对-8 D(1 D = 1 m-1)眼镜片进行了设计、仿真和加工，将理论结果与测量结果进行对比，验证设计方法的可靠性。

1 非球面眼镜片设计理论基础

1.1 旋转对称非球面

二次曲面由圆锥曲线绕z轴旋转而成，其表达式为

式中：z是表面的矢高；y是镜片到光轴的距离；r0是曲线顶点处的曲率半径；p是二次曲面系数，且p=1-e2(e2表示与球面的偏移量)。p的取值决定了整个曲面的形状，当p＞1时为扁椭圆，p=1时为球面，0＜p＜1时长椭圆，p＜0时为双曲面，p=0时为抛物面[2,6,12]。

根据式（1）可以发现，确定镜片直径大小后，r0和p是影响镜片设计的主要因素，而r0的大小由前弯决定，因此，选择合适的前弯是设计镜片的基础[13]。

1.2 光线追迹

考虑到人眼瞳孔直径较小，进入眼内的光线可视为细光束，在此条件下，Antonin等[14]提出可以采用Seidel理论来表示像差，在此基础上设计单面非球面眼镜片。该理论是像差的近似表达，只适用于涉及角度小于15°的计算，虽然能反映设计过程中像差的大致走势，但并不精确。采用光线追迹的方法可以准确计算出系统像差的大小，避免上述问题。

图1是在设计眼镜片时所用到的眼用透镜光路示意图[2,15]。其中，Z是人眼旋转中心，由于连接瞳孔中心和中央凹的线总是穿过Z，而与注视的方向无关，主光线折射后也经过该点，因此可以在Z处设置一孔径光阑来替代人眼的复杂结构，限制光束进入。O是镜片后表面的顶点，镜片位于转动中心O前27 mm处，物距设为无穷远。人眼转动角度为u2′，在此模型下可简化为轴外光线斜向入射到Z点，与光轴形成u2′的夹角，后续像差都是基于此角度下的计算。主光线和近轴边缘光线分别交像面于Q′和q′点。

图1 眼用透镜光路示意图Fig.1 Geometry of the ophthalmic lens

像散ΔFO（OAE）描述了子午面和弧矢面屈光力之间的差异，可用式（2）表示；平均斜轴差ΔFM（MOE）描述了子午面和弧矢面的平均屈光力与后顶点屈光力之差，可用式（3）表示。这两个概念均可用于评价眼镜片的光学性能。

式中：FT′和FS′分别为子午和弧矢方向的屈光力；Fv′为镜片后顶点屈光力。

为确定光线在各表面的入射角和折射角，采用式（4）所示光路计算基本公式对光线进行反向追迹。可以看作由Z点斜向出射的光线与光轴的夹角为u2′，先后在镜片的后表面、前表面发生折射，而后在前表面D点处出射。

式中：i和i′分别为入射角度和出射角度；n和n′分别为入射和出射介质的折射率。

完成初步的反向追踪计算后，可以得知光线在每个面上的入射、出射角度等信息，在此基础上计算子午、弧矢方向上的屈光力FT′和FS′，其值为镜片在子午和弧矢方向焦距的倒数。为计算人眼转动u2′时两个方向的焦距，采用如式（5）所示的Coddington方程对光线进行正向追迹：

式中：s和t分别为弧矢和子午方向的焦距；rS和rT分别为弧矢和子午方向的曲率半径，其表达式可由式（1）推导得出。根据计算所得的s和t可推导得到两主方向上的屈光力，进而可计算出OAE的值。

如图2所示，理想像MQ和真实像MQ′之间的距离QQ′即为畸变q′，MQ和MQ′的大小可由图中的几何关系推出，其表达式为

图2 镜片畸变示意图Fig.2 Distortion of the lens

上述方法适用于单面非球面和双面非球面镜片，本文选择将眼镜片的内表面作为非球面来优化其光学性能，减薄边缘厚度。

1.3 遗传算法

由于像散对视觉清晰度影响较大，因此将其作为优化的首要目标。尽管非球面镜片的畸变比球面镜片的畸变更小，但当像散被消除后，畸变会变得明显，尤其是对于高度近视患者而言，周边区域的畸变会导致配戴者视物扭曲严重，产生强烈不适感。因此降低畸变对于眼镜片的设计而言是有意义的。然而，完全消除畸变的条件较为苛刻，难以实现，且畸变减小的同时像散会增加，因此无法通过改变镜片结构参数同时消除像散和畸变。

平衡这两种像差的问题可视为多目标优化问题，非支配排序遗传算法（NSGA-Ⅱ）可用于解决此类问题，帮助平衡像差之间的关系。该算法的基本原理是模拟自然选择和遗传中选择、交叉和基因突变的现象，虽然不能得到单一的解使得两目标函数均达到最小值，但通常有一组解可以使各个目标值折衷，称为Pareto解集。每次迭代过程中只保留优秀的个体，经过上百次的迭代，即可进化出最符合设计目标的结构参数[16]。

在设计过程中，将前弯和后表面非球面系数作为变量，将OAE和q′作为优化目标函数。类比于遗传过程，个体就像染色体，自变量就像基因，随机生成N组变量，就构成了初始种群P0。通过非支配排序法对P0进行排序，计算目标函数的拥挤度后，用二进制竞标赛法将N个个体进行比较，筛选出适应度值最好的个体，即能使像散和畸变均较小的结构参数，将这些优秀个体转移到下一种群中，进行选择、交叉、变异三项遗传基本操作后，可得到第一代子代种群Q0。

将父代种群Pi和子代种群Qi合并，形成一个种群大小为2N的新种群，对其中的个体进行快速非支配排序，同时计算每个支配层的个体拥挤度，采用精英策略按照Pareto等级从低到高、每层中个体拥挤度从大到小的顺序将前N个个体放入新的父代种群Pi+1中，确保只有接近设计目标的结构参数才能进入下一迭代。对种群继续进行基本遗传操作，不断生成新的子代，直至程序满足结束条件[7,8,17]。NSGA-Ⅱ算法的流程如图3所示。经过Gen次迭代，可优化出最符合设计要求的结构参数。

图3 NSGA-Ⅱ算法流程图Fig.3 Algorithm flow chart of NSGA-Ⅱ

2 结果与讨论

2.1 参数设置

本文以-8 D眼镜片为例，镜片和模型基本参数如表1所示。

表1 非球面镜片的基本参数Tab.1 Basic parameters of the aspheric lens

NSGA-Ⅱ模型中的基本参数如表2所示，OAE和MOE线性相关，因此为保证算法的优化效率，只将OAE和q'作为优化目标。遗传算法不依赖于初始结构的选择，只需根据以往文献报道给出各参数的取值范围[6,18-19]。

表2 NSGA-Ⅱ模型参数设置Tab.2 Settings of NSGA-Ⅱ Model

2.2 仿真和实验结果

-8 D球面透镜的前弯在0 ～6 D范围内变化时，其像散和畸变变化情况如图4所示。随着前弯的增大，30°处的像散逐渐减小，在4.80 D时像散为0，随后继续增大；畸变随前弯的增大而减小，在-6%时趋于饱和。这说明当前弯为4.80 D时该球镜为无像散系统，然而这个弯度对于眼镜片而言过大，形状较凸，从安全性和美观性的角度而言，不适合用于眼镜片设计中。

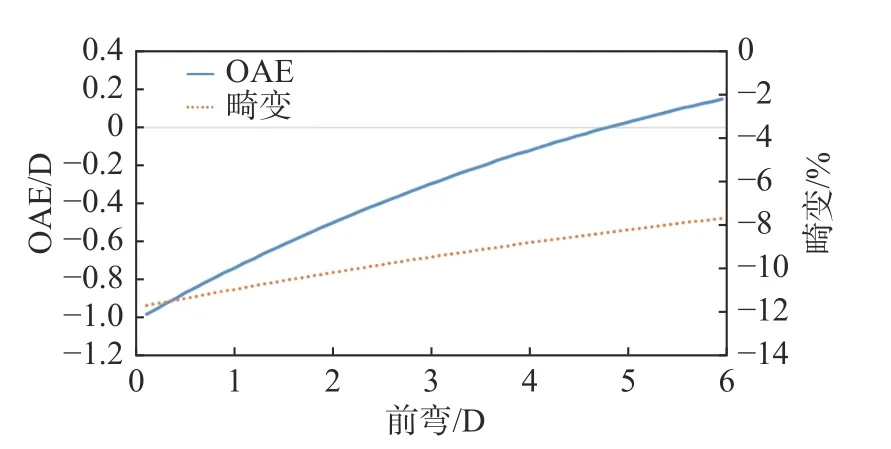
图4 球面透镜前弯变化时像散和畸变的变化情况Fig.4 Trend of astigmatism and distortion when the base curve of the spherical lens changes

本研究将前弯范围设置为0.50 ～2.60 D来避免上述问题，此时前表面相对而言较平，对于负透镜而言，后表面对镜片光学性能的影响更大，因此将后表面设为非球面。首先采用NSGA-Ⅱ多目标优化算法优化得出该范围内符合设计要求的前弯，并粗略计算其对应的非球面系数p，结果如表3所示。

表3 不同前弯的－8D非球面透镜对应像散和畸变大小Tab.3 Astigmatism and distortion corresponding to different base curve of -8D aspherical lens

从表3可以发现，当前弯为1.7～2.60 D时，OAE的绝对值均小于0.20 D，畸变在8.8%～9.5%之间浮动。而在相同的前弯下，球面透镜的OAE绝对值和畸变分别为0.30～0.55 D和9.7%～10.4%，这表明相比于球面镜片，非球面镜片的光学性能有显著提升。

在实际生产过程中，会根据订单的需求选择前表面为球面的毛坯，这些毛坯的前弯往往是几个固定值，用自由曲面车床对毛坯的后表面进行切削后得到所需镜片。由于遗传算法中初始种群是随机生成的，因此每次计算得到的前弯都不尽相同，但都集中在某一范围内，根据实际毛坯的库存情况，选择前弯在该范围内的毛坯进行加工。对于-8 D镜片，选取2.19 D作为镜片的前弯。

再次将p作为变量进行优化，可得到光学性能更优的镜片结构。优化后的p集中于-0.35～0.1范围内，这说明在2.19 D的前弯下，当p处于该范围内，镜片的像散和畸变都较小。OAE的绝对值均小于0.20 D，即便畸变在9%～9.35%间浮动。如表4所示，根据OAE的不同，选取了三组结果，其OAE分别为0 D、0.1 D和0.2 D。在-0.35～0.1范围内，随着p值的增大，OAE不断减小，而畸变随之增大。当p为0.093时，OAE为0，最小弥散圆位于视网膜上，而对应的畸变为9.33%，相对而言略大。但相比球面镜片，三组镜片的像散和畸变均有所减小。

将表4中的三组数据代入式（1）中，可计算出镜片前后表面的矢高分布。镜片的边厚可根据矢高计算得到。相比球面透镜，A、B、C三组镜片的边厚分别减少了7.88%，9.80%和10.76%。根据矢高对镜片的光焦度分布情况进行仿真，结果如图5所示，左图和右图分别为镜片在60 mm直径范围内球镜度、柱镜度的分布情况。可以发现镜片A没有像散，但畸变相对较大，边厚也是三组中最厚的，柱镜度最小，为-1.51 D；镜片C是最薄的，但其最大柱镜度为-1.98 D，是三组中最大的，这意味着镜片光焦度从中心到边缘变化最快，这会使配戴者用边缘区视物时产生眩晕等不适感；镜片B的光焦度变化程度相比镜片C更平缓，厚度比镜片A更薄。

图5 不同设计的-8 D镜片仿真图Fig.5 Simulation of -8 D lenses with different design parameters

表4 优化后三组镜片的光学性能Tab.4 Three groups of structural parameters with different optical performance

从镜片的边缘厚度来看，镜片B比镜片A薄0.18 mm，镜片厚度越薄，重量就越轻，配戴时对鼻梁的压迫就越小，这对高度屈光不正患者尤其有意义。但镜片A的光学性能更好，其像散为0，MOE也是三种设计中最小的，这意味着镜片所成的最小弥散圆最接近人眼视网膜，成像质量更佳。根据图6可以发现，虽然本设计方法是针对30°角度处光学性能的优化调整，但在该范围之内的OAE最大不超过0.1 D，而球镜的OAE则随转动角度的增大而增大，在30°边缘处OAE可达0.45 D；子午和弧矢方向的屈光力很接近，在30°处重合；两种设计镜片的畸变均随角度的增大而增大，在10°范围以内基本一致，但在10°之外的区域非球面镜片畸变比球镜更小。这说明镜片A设计的周边区域像散比球镜小，全视场范围内的成像质量都符合设计要求。

图6 30°区域内镜片光学性能对比Fig.6 Optical performance comparison of lenses in 30° region

Sun等[6]采用阻尼最小二乘法来优化镜片，虽然镜片的像散几乎为0，厚度也显著降低，但畸变甚至比球面透镜更大；且镜片的前表面是一个平面，并不是作为眼镜片的最佳选择。且采用阻尼最小二乘法前，需要确定初始结构参数，以此作为基础进行优化，这需要设计者有一定的设计经验，否则会使优化陷入局部最小值，从而无法获得满足设计要求的结构。根据李蕊等[20]所采用的镜-眼模型，采用光学设计软件设计一个同样的-8 D镜片，其前表面曲率半径r1初步定为300 mm，后表面曲率半径r2采用光焦度求解方式确定，人眼转动角度为30°，中心厚度、折射率等参数与表1中的数据一致。将镜片后表面的非球面系数和r1作为变量，在默认评价函数中将边厚最大值限制为9 mm，将降低光斑半径作为优化目标，用阻尼最小二乘法对其进行优化，易得到图7所示结果。优化后的r1为79.5 mm，换算成前弯为8.4 D，前表面形状过凸，导致整个镜片边缘处越过了人眼前表面；且该镜片后表面周边区为平面，平面和曲面之间存在连接点，不光滑，不利于加工；虽然整个系统的均方根（RMS）光斑半径为9.9 μm，光学性能有所提升，但该结构不适合作为眼镜片使用，需要对系统作进一步调整后才能得到符合要求的设计结果。而遗传算法不需要构建初始结构，降低了对设计人员的要求，把目标评价函数代入程序即可进行设计，操作简单且结果更优。将镜片A的设计参数代入上述模型中，系统结构如图8所示。-8 D近视状态下的裸眼RMS半径为95.7 μm，而戴镜后RMS光斑半径为13.5 μm，成像质量显著提升；虽然提升幅度不如最小二乘法所得结果，但镜片结构更为合理，面型光滑，无反曲点，易于加工，更适合作为眼镜片使用。

图7 采用阻尼最小二乘法优化后的光路结构Fig.7 Optimized structure with damping least squares

图8 镜片A的光路结构Fig.8 Structure of lens A

从仿真结果看，镜片C的光度分布情况最不符合设计要求，因此只将镜片A、B和球面透镜用数控自由曲面加工车床进行加工，并用面型测量仪（VM-2000）来测量60 mm直径内的光度分布情况，测量结果如图9所示。镜片A和B的球镜度从中心向边缘分别改变了2.00 D和2.50 D，镜片边缘处最大柱镜度分别为-1.25 D和-1.75 D。与仿真结果相比，变化趋势相同，变化量约有0.25 D的误差，但在可接受范围内。使用焦度计（NIDEK LM-600P，日本）测量镜片A和B的中心光焦度，结果分别为-7.98 D和-7.99 D，与设计值的误差为0.02 D和0.01 D，在允差范围内。

图9 不同设计的-8D镜片测量光度分布图Fig.9 Measurements of power of -8D lenses with different design parameters

通过设计-8 D镜片，可以发现NSGA-Ⅱ算法可以有效优化非球面眼镜片的光学性能。为进一步验证设计方法的有效性，利用该方法设计了-5～-12 D的透镜，并计算对应的像差和厚度，结果如图10所示，可以看到所有镜片的轴外像差均有所降低，边缘厚度平均减少了8.5%。

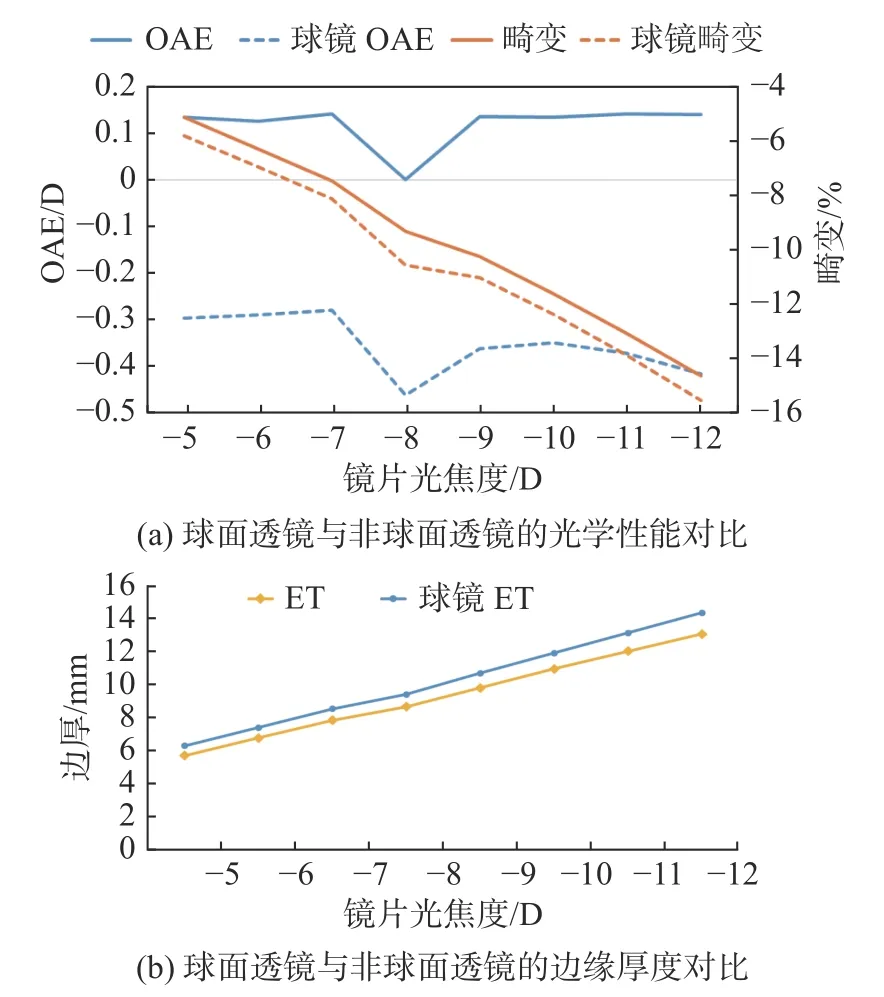
图10 -5～-12 D镜片设计结果Fig.10 Design results of lenses with different power of -5 to -12 D

本研究采用的设计方法中，像散虽然并没有完全消除，但仍在人眼可接受范围内，且畸变比球面透镜小；对前弯进行了优化，使镜片呈新月形，不仅有助于提升镜片的光学性能，也使镜片外观更美观。此外，大部分研究进行理论分析和仿真，而本研究中对设计的镜片进行了加工和测试，通过实践证明了理论的可行性，对镜片实际生产具有指导意义。

3 结 论

本文重点研究了通过改变非球面镜片的结构参数来降低其像散和畸变，采用光线追迹计算眼镜片的像差，改变前弯和非球面系数后像差得以减小，然而随着像散的减小，畸变随之增大。为解决该多目标优化问题，引入NSGA-Ⅱ算法来平衡像差以获得更好的视觉效果。本文重点阐述了-8 D镜片的设计过程，并得出以下结论：

1）眼镜片的畸变随前弯的增大而减小，并趋于一个固定值，不能完全消除；

2）对于单面非球面透镜，不能同时消除多个像差，本文将像散作为最主要的像差进行校正；

3）采用双曲面作为镜片后表面是最适合负透镜的形式；

4）通过模拟自然选择的过程，将光线追迹与NSGA-Ⅱ算法相结合，可以有效计算出多组参数，从中筛选出像差小、厚度薄的镜片结构参数。

本文还将理论结果与实际生产情况相结合，具有实际应用价值。该算法也适用于其他眼用透镜，如正透镜和柱镜。此外，还可以对高阶系数进行优化，以进一步研究其对非球面透镜设计的影响。本文中仅将后表面作为非球面，该设计方法也可应用于双面非球面镜片的设计，可获得光学性能更好、厚度更薄的镜片。