基于致灾因子对称法分级的信息量模型在地震滑坡危险性评价中的应用

凌晓，刘甲美，王涛，朱月琴，袁玲玲，陈扬洋

(1.中国地质大学(北京)信息工程学院，北京 100083；2.中国地质科学院地质力学研究所，北京 100081；3.新构造运动与地质灾害重点实验室，北京 100081；4.中国地质调查局发展研究中心，北京 100037)

0 引言

地震是诱发滑坡的重要因素，强震可在短时间内诱发大量滑坡，加剧地震所造成的损失，因此对于地震滑坡的研究具有很强的社会和学术意义[1-2]。滑坡危险性评价方法大体上可分为定性评价[3-5]与定量评价。定量评价方法又可分为传统的统计量评价法[6-8]与机器学习评价法[9-11]。定性评价依赖于专家经验[12]，客观性较差，而机器学习方法对于样本的数量、质量要求较高，且需要频繁进行迭代运算与参数调整，不适用于较大的研究区。因此，传统的统计量评价法仍被广泛应用于地震滑坡的危险性评价。

1948年Shannon[13]发表的著名论文《通信的数学理论》标志着信息科学的诞生，Shannon把信息定义为“随机事件不确定性的减少”，并把数学统计方法移植到了通信领域，提出了信息量的概念及信息熵的计算公式。在此基础上,Van[14]提出了信息量模型，这是一种较为客观、适用性较强的统计预测方法，具有分析尺度大、建模流程简单等优点。国内外已有很多学者利用信息量模型进行滑坡危险性评价[15-19]。在信息量模型建模过程中，首先应制定因子分级标准，为了确保结果的准确性，需预先进行单因子统计分析。大部分研究者结合单因子分析结果，采用等间距法进行因子分级，少数研究者则采用自然间断法进行因子分级[19]。这些方法具有一定的科学性，但忽略了因子的复杂性和多样性，不能最大限度地发挥单因子分析的优势。如何充分考虑致灾因子的特征，结合单因子分析结果制定出最合适的因子分级方法，提高评价结果的准确性，是利用信息量模型评价滑坡危险性时亟待解决的问题。为了加强对单因子分析的利用，从而提高信息量模型的评价精度和适用性，本文提出了一种新的合并对称区间进行分级的方法，并以汶川地震滑坡密集区为研究区，用该方法构建的信息量模型进行了地震滑坡危险性评价。

1 对称法分级与信息量模型构建

1.1 模型构建原理

在信息论中，信息熵是接收到每条消息中包含的信息的平均量；在信息量模型中，地质灾害危险性可由信息熵度量。信息预测的观点认为，滑坡的发生是多种致灾因子相互耦合、共同作用的结果[20]。因此在应用信息量模型评价滑坡危险性时，可将滑坡危险性视为多个因子的信息熵叠加值。信息熵以概率倒数的对数函数计算，即

(1)

式中：I(y，x1x2…xn)为在(x1x2…xn)组合下产生的总信息量；P(y，x1x2…xn)为在(x1x2…xn)组合下事件发生的概率；P(y)为事件发生的实际概率。

在进行滑坡危险性研究时，信息量模型公式中的条件概率可简化为样本频率，即滑坡面积与研究区总面积的比值。信息量模型的表达式为：

(2)

式中：x为任一致灾因子；n为因子x的分级总数目；I(x,H)为x因子对滑坡发生提供的信息量值；S为研究区评价单元的总数；Si为x的第i级区域内覆盖的评价单元数；N为研究区内滑坡单元的总数；Ni为x的第i级区域内覆盖的滑坡单元数。

当存在m种致灾因子时，总信息量I的计算公式为：

(3)

式中：I为信息量总和；m为参与评价的因子总数。总信息量值I是滑坡危险性的量化表达，信息量值越大，代表其危险性越高。

本文的研究目的为利用对称法对因子进行分级以构建信息量模型，以进行滑坡危险性评价，并验证该方法的合理性，技术流程图如图1所示。

图1 基于信息量模型的汶川地震滑坡危险性评价技术流程Fig.1 Workflow of landslide hazardness analysis in Wenchuan area using information value model

1.2 因子分级原理

由式(2)可知，因子分级是信息量模型建模过程中的必要步骤。为了使有限的分级区间包含尽量多的信息，本文参照正态分布相关的统计学知识，提出了一种对称分级法。该方法以标准差分级法为基础，可有效减少分级数目，能以尽可能少的分级数突出与滑坡相关性更高的部分。标准差计算公式为：

(4)

式中：μ为均值；σ为标准差。

本文首先以标准差分割法对因子进行预分割，标准差分割法结果中往往会存在一个中心区间(定义为μ±1/2nσ，其中，n为σ的倍数，可为整数或小数)，并在此中心区间之外以nσ为间隔进行区间划分。在经过预分割后，本文对区间进行合并，以中心区间为对称轴，从外到内对左右对称的区间依次进行合并，所得到的结果即为对称法分级结果，如图2所示(以标准正态分布为例)，图中相同填充色的区间被划分为同一级。本文将预分割间隔设定为1/2σ。

图2 对称法分级示意图(以标准正态分布为例)Fig.2 Schematic diagram of the symmetrical classification method (e.g. standard normal distribution)

2 实验

2.1 研究区概况及数据源

本文选择汶川地区北川-映秀断裂带及其周边地区作为研究区，覆盖范围为E102°17′18″～105°43′12″,N30°20′6″～33°15′19″。研究区范围较广，高程范围在0～6.25 km之间，山势陡峻，地表起伏大，地形地貌变化多样；研究区内岩性种类丰富，地质构造复杂，地震烈度范围为Ⅶ～Ⅺ度；区内河流众多，包含岷江、白龙江、小泾川及其细小径流，沟谷河流遍布于山体之中，易积水，存在土壤结构疏松的区域，因此广泛具备滑坡发生的基本条件。

许冲等[21]利用2008年汶川特大型地震前后获取的高分辨率遥感影像，制定了客观、详尽的滑坡编录，该编录包含195 290个矢量面，覆盖面积达到1 160 km2。本文基础数据包括该滑坡编录、1∶25万数字地质图(公开版)、1∶100万河网图、1∶100万断裂数据、25 m空间分辨率DEM、汶川地区地震烈度矢量图等。原始数据如图3所示。

图3 研究区内基础地理数据Fig.3 Original geographical data of study area in Wenchuan

在开始实验之前，首先对多源数据进行预处理，本文对于矢量数据中冗余的属性进行了清洗，统一了数据格式、栅格分辨率、参考系；随后，将多源数据处理为多源致灾因子，因子图均为栅格格式，空间分辨率为25 m。由于坡度0°～10°之间的区域地势较为低缓，发生滑坡的可能较低，多分布滑坡堆积物，本文研究中没有对该区域进行分析。

2.2 单因子统计分析

根据对前人研究的整理归纳[4～27]，本文选取了9个致灾因子，选取依据与数据源见表1。本文采用ArcMap10.2软件将栅格化后的滑坡图与对应的致灾因子图相叠置，以获取各个致灾因子与滑坡面积的关系。由于本文研究区面积较大，滑坡分布广泛，因此在进行单因子分析时，需要进行由粗放到细致的多次叠置分析，以达到精细分析的目的。

表1 致灾因子的详细数据源与选取原则Tab.1 Selection principles and original data resources of hazardness factors

(续表)

2.2.1 坡度

研究区内的坡度范围由10°～89.3°。由图4可知，滑坡的面积随着坡度的增大呈现正态分布变化趋势，其中，分布于坡度35°～45°区域内的滑坡面积所占比例最大。

2.2.2 坡向

本文将坡向以45°为间隔分为8个方向，以337.5°～22.5°为北坡。坡向的单因子统计分析结果如图5所示，大部分滑坡发生在东坡与东南坡上，与前人的研究结论[24]相吻合。

图5 坡向与滑坡之间的关系Fig.5 Statistical analysis results between landslide and aspect

2.2.3 高程

在本文研究区内，滑坡大多分布在高程0.522～5.307 km的区域内。由图6可以看出，随着海拔高度的增加，滑坡面积呈现先上升后下降的趋势，滑坡集中分布在高程1～2 km范围内，在这个区间内存在较为明显的拐点；在高程超过4 km后，滑坡显著减少。

图6 高程和岩性与滑坡之间的关系Fig.6 Statistical analysis results between landslide and height

2.2.4 到断层距离

本文围绕汶川地震主发震断裂北川-映秀断裂构建了25 km的缓冲区，分析了不同断层距离范围内滑坡面积的分布，结果如图7所示。随着到断层距离的增加，发生的滑坡面积相应减小，曲线有较明显的拐点，分别位于5 km，11.5 km以及15.5 km处；在超过15 km后，滑坡面积的变化幅度减小，基本不会随着到断层距离的增加而明显下降。

图7 到断层距离与滑坡之间的关系Fig.7 Statistical analysis results between landslide and distance to fault

2.2.5 地表曲率

在研究区内，大部分滑坡发生在曲率范围为-0.05～0.05之内。本文选取该部分，以0.003为间隔再次对区间细分，进行统计。由图8可知，地表曲率与滑坡面积的关系近似呈正态分布。大部分滑坡分布在水平曲率-0.01～0.01、剖面曲率-0.015～0.015的范围内。

(a)水平曲率 (b)剖面曲率

2.2.6 岩性

本文以汶川地区地质图为底图，将岩性由坚硬到软弱分为5个大组，编号1—5，依次代表极坚硬岩组、较坚硬岩组、坚硬岩组、较软弱岩组、极软弱岩组；每个大组又按相对强弱细分为3个小分组，编号Ⅰ—Ⅲ，分组与对应的典型岩性类型如表2所示。分析结果如图9所示，可以看出，滑坡高发地区的岩性大多为极坚硬岩组的坚硬组，坚硬岩组的较软组，较坚硬岩组的坚硬组和软弱岩组的坚硬组。

表2 岩性分组及其对应的部分代表岩性Tab.2 Classification result of lithology and examples matching each group

图9 岩性和岩性与滑坡之间的关系Fig.9 Statistical analysis results between landslide and lithology

2.2.7 到河流距离

本文将河流缓冲区设置在0～3 km之内；在3 km之后，可认为受河流的影响基本可以忽略不计，分析结果如图10所示。随着到河流距离的增加，发生的滑坡面积相应减小；在距离1.7 km以外，曲线呈较为平缓趋势。

图10 到河流距离与滑坡之间的关系Fig.10 Statistical analysis results between landslide and distance to river

2.2.8 地形湿度指数

地形湿度指数计算公式为：

(5)

式中：ITW为地形湿度指数；As为汇水面积，可通过流量得到；β为坡度，在实际计算中，需将坡度由角度制转为弧度制。

本文根据式(5)计算地形湿度指数。经分析后可知，滑坡大部分分布在地形湿度指数值为3～10的区域内。本文选取该范围，以0.3为间隔对区间进行细分，结果如图11所示。地形湿度指数与滑坡面积的关系呈现正态分布，地形湿度指数在6～8之间区域内的滑坡面积较大。

图11 地形湿度指数与滑坡面积之间的关系Fig.11 Statistical analysis results between landslide and topographic wetness index

2.2.9 地震烈度

本文采用汶川地震发生后中国地震局实地调查获取的地震烈度分布图，分析结果所如图12所示。可以看出，随着地震烈度的增大，滑坡面积呈现增加趋势，在地震烈度为Ⅺ度的区域内，发生的滑坡总面积最大。

图12 地震烈度与滑坡面积之间的关系Fig.12 Statistical analysis results between landslide and intensity

2.3 信息量模型构建

在实验中，坡向、岩性、地震烈度可根据属性分类结果进行分级，无需进行分级方法探究。其余因子按照单因子统计分析结果，分为呈近似正态分布的因子(坡度、地表曲率、地形湿度指数)与非正态分布的因子(高程、到河流距离、到断层距离)。对于呈近似正态分布的因子，采用对称法进行分级；呈非正态分布的因子，遵循区间异质性最大化原则选择分级方法。

为了验证对称法的合理性，探究不同分级方法对模型评价结果的影响，本文选取了5种标准分级法进行对比试验，分别为等间距分割(equal interval，EI)、分位数分割(equal quantile，EQ)、自然间断分割(natural break，NB)、几何间断分割(geometric break，GB)和标准差分割(standard deviation，SD)。部分分级结果如图13所示(以地形湿度指数为例)。EQ，NB和GB分级数目均为10级。可以看出，对称法(图13(f))用最少的分级等级，包含了最多的信息，突出了地形湿度指数因子中与滑坡相关性更大的区域。

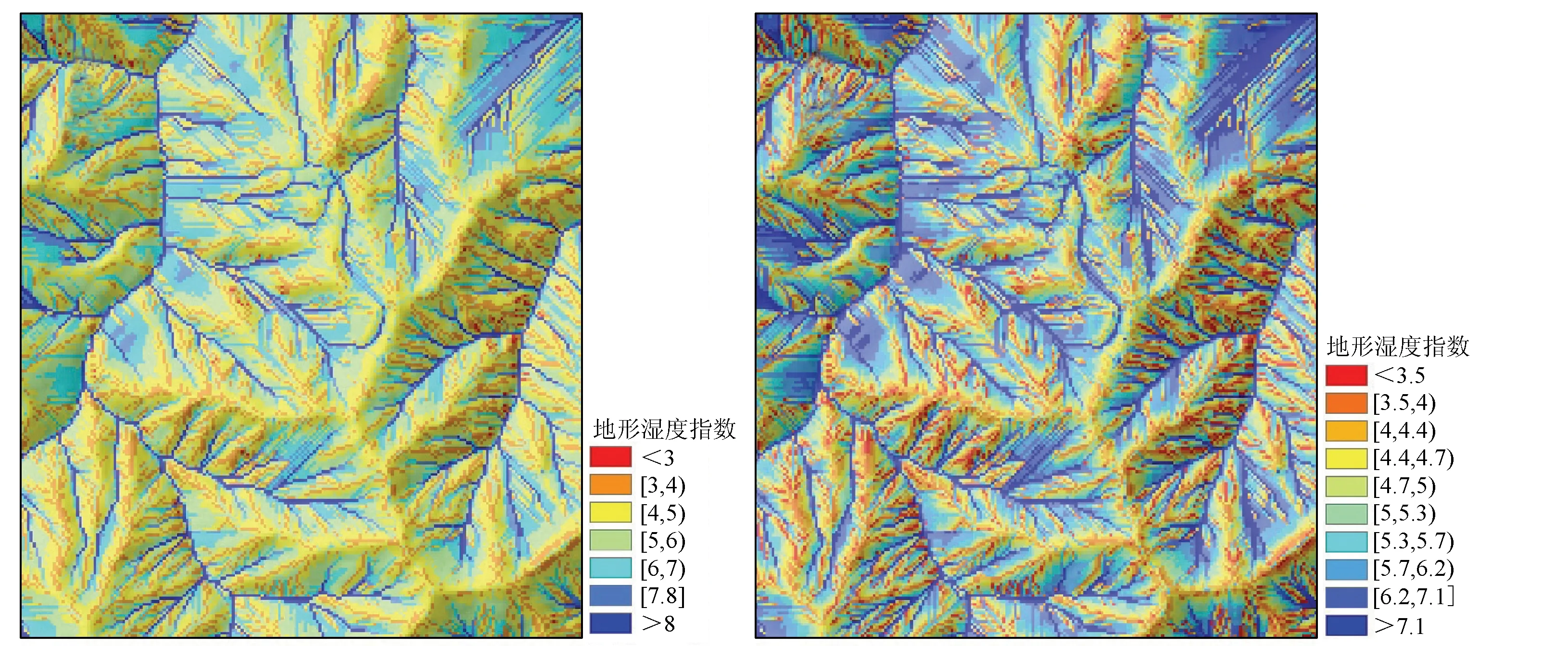
(a)EI法 (b)EQ法

(c)NB法 (d)GB法

在对因子进行分级后，按式(3)对因子的各个等级对应的滑坡面积进行统计与信息量计算。当信息量值为正值时，说明该因素对于滑坡灾害的发生有正向贡献，而信息量值为负值或0时，说明该因素对于滑坡灾害的发生有负向贡献或没有贡献。

3 实验结果与分析

将信息量计算结果乘1 000转为整形，通过重分类将因子的信息量赋值给相应的等级，随后通过叠置分析，得到结果图。由于计算结果值范围相差较大，为了方便对比，需统一范围。本文采用归一化处理，将结果范围归纳至0～1，再以0.2为间隔，将危险性图从高到低划分为危险性极低(0～0.2)、较低(0.2～0.4)、中等(0.4～0.6)、较高(0.6～0.8)、极高(0.8～1)5个等级，如图14所示。

(a)EI法 (b)EQ法 (c)NB法

(d)GB法 (e)SD法 (f)对称法

由图14可以看出，研究区内滑坡危险可能性较高的区域集中在北川-映秀断裂带两侧。其中，断层分布较为密集的地区多为山区，海拔也相应较高，地势较为陡峭，因此滑坡发生的危险性最高。将致灾因子图与该结果图对照可发现，滑坡危险性高的地区与地震烈度的Ⅹ～Ⅺ级覆盖地区、断层缓冲区0～15 km内、岩性的第一大类分布地区重合度较高。将该结果与信息量值的正值部分相对照，可发现危险性较高的地区与正向贡献的因子及其对应等级基本相吻合。

图14(f)表明，利用对称法分级所得到的滑坡危险性评价图中较高、极高危险性区划地域所占面积比例相对较大，因此危险性等级的区分度更高。为进一步验证对称法的优越性，本文统计了6种分级方法的结果中危险性较高、极高区域内的实际滑坡面积的比例(表3)。

表3 危险性较高和极高区域内实际发生滑坡面积的大小和比例对比Tab.3 Comparison of the proportion of actual landslide area in high-risk and extremely high-risk areas (%)

通过将表3中较高、极高危险区划内滑坡面积比例相加可以得到6种分级方法的结果，分别为：EI法79.24%，EQ法79.61%，NB法74.79%，GB法68.65%，SD法68.81%，对称法80.87%。利用对称法构建模型的制图结果中，覆盖于危险性较高和极高区域中的实际发生滑坡面积比例最高，说明对称法充分利用了单因子分析的优势，具有较好的分级效果。

4 结论与讨论

为最大限度地发挥单因子统计分析的优势，提高信息量模型的评价准确性与适用范围，本文提出了一种合并对称区间进行分级的方法，并利用该方法构建信息量模型，对汶川地区的地震滑坡危险性进行了评价。为了验证对称法的合理性，本文选取了5种标准分级进行建模，将所得到的结果进行对比，得出结论：

1)通过单因子分析可知，滑坡面积与坡度、地表曲率(水平曲率和剖面曲率)、地形湿度指数之间的关系呈现正态分布，即分布于因子范围两侧区域内的滑坡面积较小，分布于中部区域中的滑坡面积较大。

2)研究区内滑坡危险较高、极高的区域集中在北川-映秀断裂带两侧，该范围内山区分布众多，地势较为陡峭，海拔也相对较高，与灾害信息量值呈正值的区域大致相同。

3)对称法得到的危险性区划图中，较高、极高危险区覆盖实际滑坡面积比例最大，达80.87%，高于其他标准分级方法所得的结果。这表明，对称法分级结果能够充分利用单因子分析的优势，突出危险性较高的地区，便于决策者快速锁定危险性较高和极高的区域。

应该指出，对称法存在着一定局限性，即假定因子与滑坡的关系呈近似正态分布状。然而，因地质灾害规模的不同，滑坡面积与因子的关系大多不符合标准正态分布，甚至可能呈现离散分布(地质灾害规模较小)，在这些情况下对称法是否仍旧适用，还有待进一步研究与讨论。

志谢：本文所使用的汶川地震滑坡编录数据由中国地震局地壳应力研究所许冲研究员提供，对此深表谢意。