基于全角模式下硅微轴对称陀螺调频控制技术
杨颖慧,刘 靖,卜 峰,樊 波,徐大诚,郭述文
(苏州大学电子信息学院,江苏苏州 215006)
0 引言
MEMS陀螺仪作为测量运动物体惯性的器件,因其具有成本低、尺寸小和质量轻等特点,广泛应用于汽车工业,惯性导航和智能手机等领域[1]。轴对称MEMS陀螺的工作模式分为速率模式[2-3]和速率积分模式(又称全角模式)[4]。全角模式通常采用幅度调制(amplitude modulation,AM),将角速率信息调制到2个振动模态的位移上,通过幅度解调来得到进动角。相比速率模式,它具有量程大、宽带宽和标度因子稳定等优点。然而,MEMS陀螺存在结构加工工艺误差带来阻尼和刚度不匹配问题[5],会导致较大阈值。2018年,T. Parsa等[6]提出使用与进动角相关偏置误差进行补偿来降低阈值的方法,最终阈值为3(°)/s,但是该阈值仍然较大且补偿方法比较复杂。
除了幅度调制工作模式之外,T. Tsukamoto[7]提出一种全差分频率调制(frequency modulation,FM)陀螺,在单个谐振子上独立控制顺时针(clockwise,CW)和逆时针(counter clockwise,CCW)的叠加模式,使用CCW和CW解调器,同时控制这2种模式。该控制系统可以检测输出角度或角速率。但是该方法存在顺逆时针模式相互耦合的问题,导致阈值较大。在高Q值陀螺中还存在系统稳定时间长问题。该学者后面提出算法补偿来降低顺逆时针模式相互耦合[8],但是方法比较复杂且不能实现实时补偿。
针对以上问题,本文在调频陀螺控制系统基础上对其进行了优化。在现有调频全角控制系统上添加了AGC模块,用于控制顺逆时针振动模式幅度,从而实现振动模态频率的迅速稳定并且减小了顺逆时针模式相互耦合,显著降低了角度检测阈值。
1 调频控制技术
1.1 轴对称类蛛网式陀螺
本文以轴对称类蛛网式圆盘谐振陀螺(cobweb-like disk resonator gyroscope,CDRG)[9]为实验对象,陀螺结构如图1所示。CDRG的特点是结构对称性好,频差小且Q值高,初始频差仅为1.66 Hz,Q值可达到13万,频差和Q值测量曲线如图2所示。经过静电调谐之后,频差能降低到0.1 Hz以下[10]。

(a)CDRG的结构示意图(b)x和y模态的振型图图1 陀螺结构图
1.2 全角模式下的调频技术
MEMS陀螺通常以二维弹簧阻尼振动系统来建模,模式匹配下的陀螺动力学方程为:

(1)
式中:x和y分别为x模态和y模态方向上的振动位移;Ω为输入角速度;ω0为共振频率;k为角增益,由陀螺的几何结构决定。
式(2)是陀螺动力学方程对应于旋转坐标系的幅度归一化通解:
x=sin(ω0t)cos(kΩt)+sin(ω0t+φ)sin(kΩt)
y=-sin(ω0t)sin(kΩt)+sin(ω0t+φ)cos(kΩt)
(2)
式中φ为x模态和y模态方向上振动位移的初始相位。
通过三角恒等变换,式(2)可重新表示为:
x=Aω+Ωsin((ω0+kΩ)t+φ1)+Aω-Ωsin((ω0-kΩ)t+φ2)
y=Aω+Ωsin((ω0+kΩ)t+φ3)+Aω-Ωsin((ω0-kΩ)t+φ4)
(3)
式中:

(4)
式(3)中,表达式的x和y可以看做是2个正弦波信号的叠加,频率分别是ω0+kΩ和ω0-kΩ,其中角速率信息Ω就被调制到共振频率上ω0。式(4)是正弦波的振幅表达式,每个正弦波的振幅通过参数φ来决定陀螺运动轨迹。图3是陀螺质量块运动轨迹图,可以看出,对于不同的φ,有3种不同的陀螺运动轨迹,分别是直线、椭圆和圆形。

图3 在不同初始相位下陀螺质量块的运动轨迹图
本文选择的陀螺质量块运动轨迹是顺时针圆形轨道频率为ω0+kΩ和逆时针圆形轨道频率为ω0-kΩ来进行调频全角操作,通过对ω0+kΩ和ω0-kΩ差分读出可以消除共振频率ω0的影响。
2 调频全角控制技术的分析与改进
在本文控制系统中,设定ωcw=ω0+kΩ,ωccw=ω0-kΩ。在1个谐振子上,用cosωcwt和cosωccwt驱动x模态,-sinωcwt和sinωccwt驱动y模态,2个锁相环(phase lock loop,PLL)将顺逆时针模式控制在谐振状态,2个AGC分别控制顺逆时针幅度。根据2个PLL频率信息,进行相干解调和三角函数运算得到角度输出,控制框图如图4所示。

图4 调频全角模式系统控制框图
顺时针闭环控制中PLL频率输出是ωcw,逆时针闭环控制中PLL频率输出是ωccw,角度检测过程如下:
(5)
(6)
将上述2个信号经过低通滤波器滤除频率为2ω0的高频信号,经过三角函数运算得到角度:

(7)
根据上述分析过程可以看出,PLL的频率输出(ωccw和ωcw)直接反映角度信息,差分读出消除共振频率ω0的影响同时频率稳定影响角度检测输出。
为此,本文添加2个AGC环路,目的是让陀螺的振动幅度迅速稳定,并且让顺逆时针模式振幅相等。在实际情况下,陀螺存在各种误差,如阻尼和刚度误差等,陀螺的动力学方程实际为:

(8)
式中mx,my,bx,by,kx,ky分别为陀螺x模态和y模态的质量,阻尼和刚度。
由于顺逆时针振动模式是对称的,这里以逆时针模式分析为例。当逆时针模式单独工作时,假设系统的解为正弦信号,这里将x和y模态方向上位移的解表示为向量形式,即x=xccw(t)ejωccwt,y=jyccw(t)ejωccwt,xccw(t)和yccw(t)代表x模态和y模态方向上位移的振幅,反馈力Fx=jFxccwejωccwt,Fy=-Fyccwejωccwt用于控制振幅和相对相位,将这些公式带入式(8),利用欧拉公式将系统分为实部和虚部,可以得到:
(9)
(10)
通过向量分析,计算出频率的表达式[11],在不考虑阻尼误差的情况下,最终得到逆时针模式的频率表达式为
(11)
同理分析可以得到顺时针模式的频率表达式为
(12)
xcw(t)和ycw(t)为顺时针模式下x模态和y模态方向上的振幅。xccw(t)、yccw(t)、xcw(t)和ycw(t)都是与e指数相关的时间函数,随着时间上升,它们会趋近于一个常数。由式(11)和式(12)可以看出顺逆时针模式的PLL频率输出与x和y模态振幅相关,即振幅会影响频率输出准确性,进而影响角度检测。为此,需要保持振动幅度快速稳定。
在调频全角控制系统中,顺时针振动模式振幅为
(13)
逆时针模式振动振幅为
(14)
式(13)和(14)可以看出顺逆时针模式振幅与x模态和y模态方向上振幅之间的关系。顺逆时针模式的振幅rcw和rccw值越接近,意味着顺逆时针模式的相互耦合越小,使角度检测输出的线性度越好[7-8]。所以本文添加2个AGC环路来控制顺逆时针模式的幅度,减小它们之间的相互耦合来降低阈值,同时使x和y模态方向上振幅快速稳定,让PLL的频率输出能够快速地跟随角速率的变化而变化。
3 测试结果与分析
3.1 测试平台与实验环境
本文实验是基于FPGA数字化测控平台实现,以CDRG为实验对象。测控电路由3部分组成:信号拾取电路、AD/DA电路及FPGA电路。测试平台如图5所示,陀螺及电路参数如表1所示。

图5 测试平台
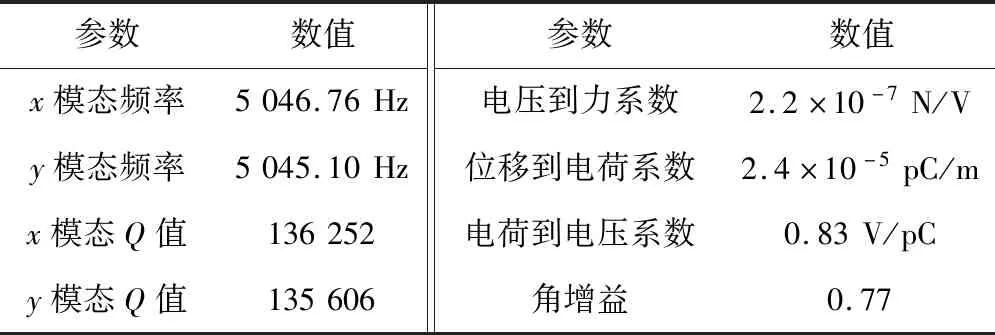
表1 陀螺及电路参数
3.2 测试结果
在Vivado上编写FPGA程序,基于测试平台上进行验证。首先,不添加AGC模块进行实验,直接给一个恒定幅度(50 mV)的正弦信号来激励顺逆时针振动模式,逆时针模式幅度输出如图6所示。可以看到在4 s处幅度趋于稳定,但是幅度输出有波动,波动幅度大小在70 mV以内。在同样实验条件下,添加AGC模块进行幅度闭环实验,结果如图7所示。逆时针模式幅度在0.4 s快速稳定,波动幅度大小在20 mV以内。逆时针模式的幅度输出有波动主要是因为陀螺2个模态间的频差,导致顺逆模式相互耦合而产生波动。实验结果证明AGC模块可以使振动模态幅度快速稳定。顺逆模式是对称的,通过实验观察,AGC能够使顺逆时针振动幅度非常接近,降低它们之间的相互耦合。

图6 未添加AGC的逆时针振动模式振幅

图7 添加AGC模块的逆时针振动模式振幅
在不同输入角速率下(±50(°)/s、±100(°)/s、±150(°)/s)检测角度输出,结果如图8所示。表2是相应的角增益 (即标度因子),可以看出,输入角速率越大,标度因子越接近陀螺结构的理论角增益0.77。

图8 不同输入角速率下的输出角度
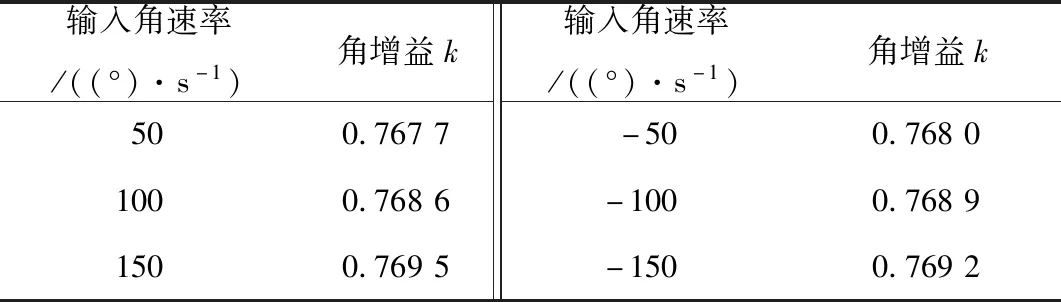
表2 不同输入角速率下的角增益
3.3 检测阈值对比
添加AGC模块后,最低角速率阈值可以达到0.5(°)/s,测试结果如图9所示,从图9可以看出,在0.5(°)/s输入角速率的情况下系统虽然可以正常输出角度,但是测试的输出角度线性度较差。未添加AGC模块能测得的最低角速率阈值是11(°)/s,且在阈值附近的角度输出线性度非常差。图10是2种控制方法的角度检测输出在角速率输入为11(°)/s时的对比实验结果,实验结果表明添加AGC模块后,显著改善了全角模式控制系统的性能。

图9 阈值附近的角度输出

图10 11(°)/s输入角速率下的2种方法角度输出
4 结束语
本文介绍了一种频率调制全角陀螺的控制系统。在单个谐振子上同时叠加陀螺质量块顺逆时针的运动轨迹,通过添加AGC闭环使顺逆时针振动幅度快速稳定且接近相等,减小顺逆时针模式相互耦合,降低了角度检测阈值。实验证明了控制系统的有效性。然而,本文控制系统中没有完全解决频差的问题,而不能完全消除顺逆时针振动模式相互耦合的影响,导致频率输出有波动。为此,在今后工作中,拟采用双陀螺控制方法来解决波动问题。

