含多类型分布式电源的主动配电网三相动态潮流算法

刘小恺，范晓龙，房文轩，米 夏，安 东

（1.内蒙古电力科学研究院，内蒙古 呼和浩特 010020；2.国网内蒙古东部电力有限公司经济技术研究院，内蒙古 呼和浩特 010010）

0 引言

为实现国家“碳达峰、碳中和”的目标，随着以清洁能源为代表的新能源被广泛开发利用，正驱动传统电网朝着高效、灵活、智能的能源互联网方向发展［1-2］，主要表现为分布式电源（Distributed Generation，DG）特别是大规模间歇式可再生能源的接入与应用。随着配电网向含大量不同类型分布式电源的主动配电网（Active Distribution Network，ADN）转变，配电网变为有源网络，由配电管理系统（Distribution Management System，DMS）进行在线实时监控。当ADN 孤岛运行时，若负荷突然增加或网络结构发生变化，松弛节点的容量可能不足以承担全部功率缺额。因此，如何通过分布式电源的调节控制对网络潮流进行管理，同时提高清洁能源的利用率，是主动配电网优化运行研究中的难点之一［3-5］。动态潮流（Dynamic Power Flow，DPF）算法可以在系统中设置多个平衡节点来共同承担系统的不平衡功率，所以能够满足分布式电源接入后主动配电网的潮流计算要求［6-8］。

文献［9-11］较早提出了基于分布式松弛节点模型的配电网三相潮流算法，通过定义参与因子使各电源动态分配网络损耗，但采用相分量形式的三相潮流算法计算时间较长，导致计算效率不高。文献［12］提出基于网损灵敏度的参与因子计算方法，在潮流计算中由降压变电站和各个分布式电源共同分担配电网有功网损，但未考虑主动配电网三相不平衡的特点。文献［13-14］仅考虑了PQ节点类型DG接入，且未考虑DG出力的限值约束条件。

基于序分量形式的潮流算法可以实现三相解耦并行计算，能够大幅提升计算速度［15-17］。因此，提出一种基于序分量的主动配电网三相动态潮流算法，并给出功率缺额分担系数的概念，由不同控制策略的DG参与分担系统的有功和无功功率缺额，同时考虑了各种DG的出力限制，使主动配电网的潮流计算更接近实际在线运行情况。

1 基于序分量的三相动态潮流算法

含DG接入的配电网系统结构如图1所示。

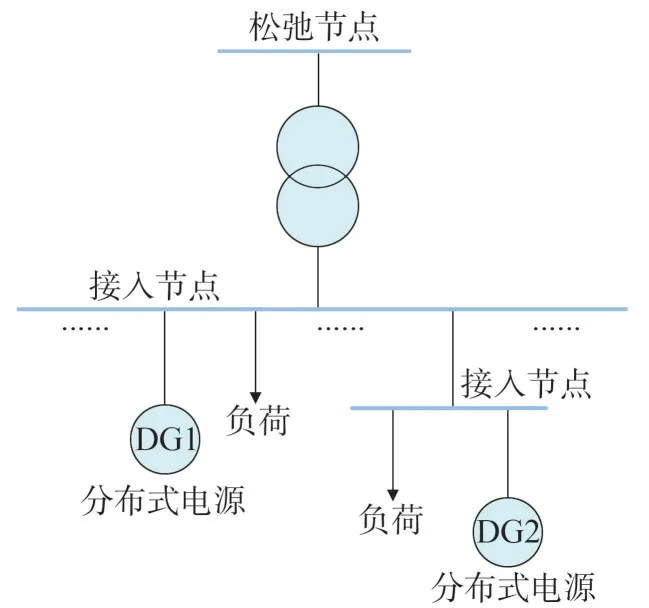
图1 含DG的配电网系统结构

在传统配电网的潮流计算中，将输配电网的公共连接点定义为松弛节点，该节点有两层含义，一是作为系统节点电压相位的参考节点；一是承担系统的功率不平衡量，即作为平衡节点。当DG 接入后，可由各类分布式电源承担平衡节点的作用，共同分担系统的功率不平衡量。

首先，利用对称分量变换矩阵T将系统状态变量由相分量形式转换为序分量形式，如式（1）所示。

式中：V120和Vabc分别为节点序分量电压向量和相分量电压向量。

1.1 功率缺额分担系数

假设节点i为主动配电网中有DG 接入的节点，在潮流计算过程中，每次迭代后DG 出力与负荷功率、线路功率损耗的正序功率缺额为：

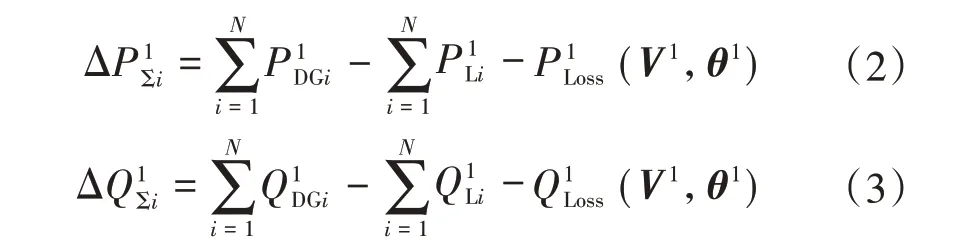
式中：N为系统的节点总数；和分别为节点i处DG 的有功出力和无功出力；和为 节 点i的负荷功率；s和分别为正序系统的有功损耗和无功损耗；V1和θ1分别为正序系统的节点电压幅值向量和相角向量。

定义Kp1和Kq1为松弛节点的有功功率缺额分担系数和无功功率缺额分担系数；Kpi和Kqi分别为DG的有功功率缺额分担系数和无功功率缺额分担系数，i=m，…，N，表示m号至N号节点有DG接入。则有：

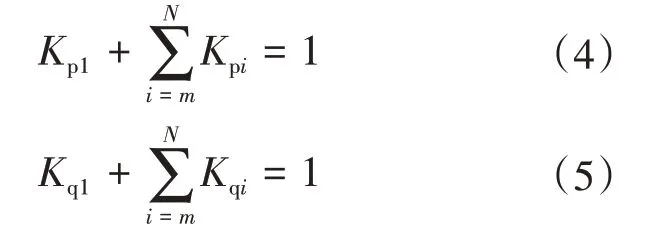
式中：当Kp1=Kq1=1时，即为常规潮流计算模式。在实际情况下，Kpi可根据DG 的频率调节特性选取，Kqi可根据DG的电压调节特性选取［8］。

1.2 序分量三相动态潮流方程

在动态潮流计算中，每次迭代后的功率缺额由松弛节点和DG按分担系数共同承担，则正序系统的动态潮流方程为：

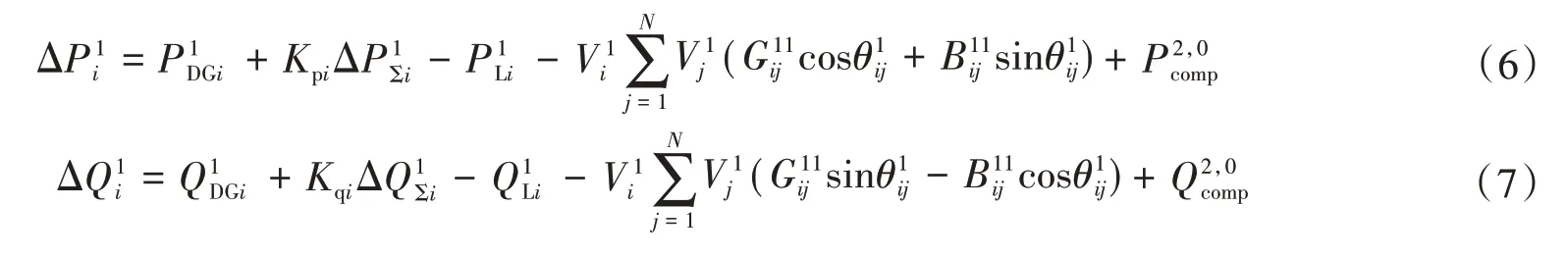
式中：和分别为节点i和节点j正序节点电压；为节点i和节点j的正序电压相角差；和分别为正序节点导纳矩阵中的电导和电纳；和分别为负序、零序系统对正序系统的补偿功率。

式（6）和式（7）与常规潮流方程的区别在于，利用牛顿-拉夫逊法进行每次迭代计算之前，需要先通过式（2）和式（3）计算功率缺额，然后按分担系数加入DG接入节点的功率平衡方程中，即可解算出正序系统的状态变量V1和θ1。

1.3 DG出力越限处理方法

在动态潮流计算中，若分担功率缺额后的DG 出力越限，则须对DG的分担系数进行如下修正：

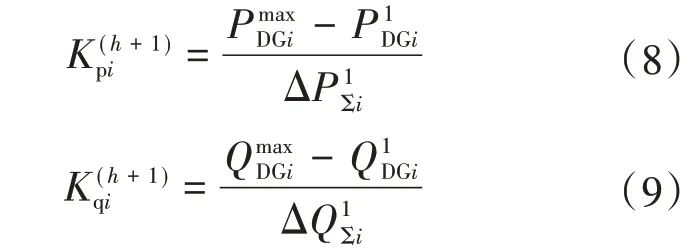
式中：h为当前的迭代次数；和分别为DG 有功出力和无功出力的上限值。

当发生DG 出力越限时，为满足式（4）和式（5），还须对松弛节点的分担系数进行调整，如式（10）和式（11）所示。

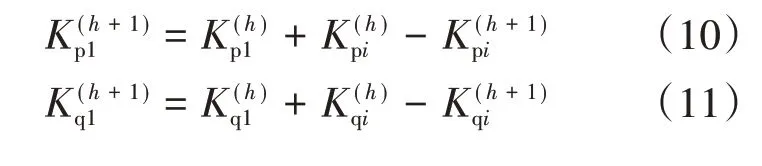
2 DG潮流模型

DG 有燃料电池、风机、光伏发电、储能装置、微型燃气轮机等多种类型，主要通过电力电子逆变器并网，如图2 所示。根据不同DG 的并网控制特性，将其分为功率控制型、电压控制型和功率因数控制型［17］。图2中，和分别为DG的三相有功功率和无功功率。

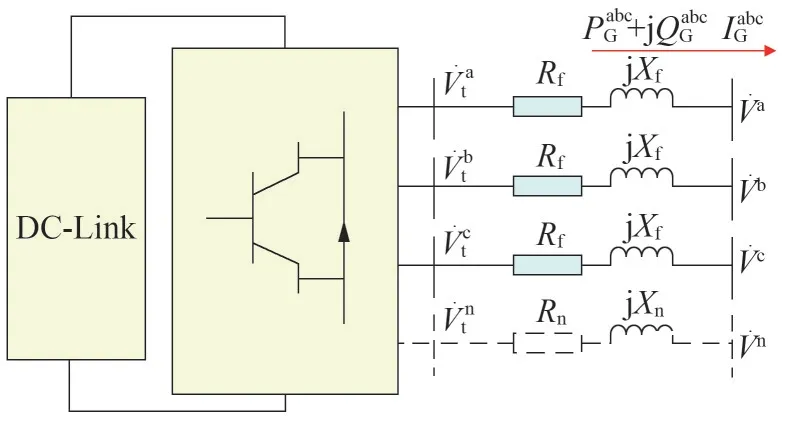
图2 电力电子逆变器并网接口

对于功率控制型DG，按PQ 节点处理，正序有功功率和无功功率的计算公式为

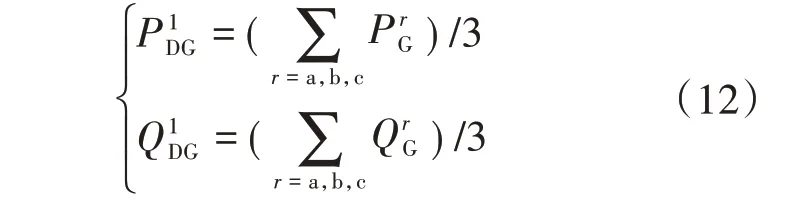
对于电压控制型DG，按PV 节点处理，正序有功功率和节点电压幅值的计算公式为

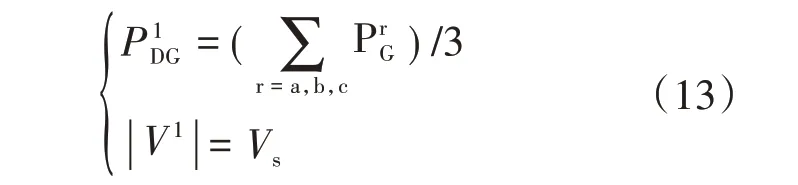
式中：V1为正序系统的节点电压；Vs为正序节点电压给定值。

对于电流控制型DG，按PI 节点处理，在潮流计算中可将其转化为PQ节点形式

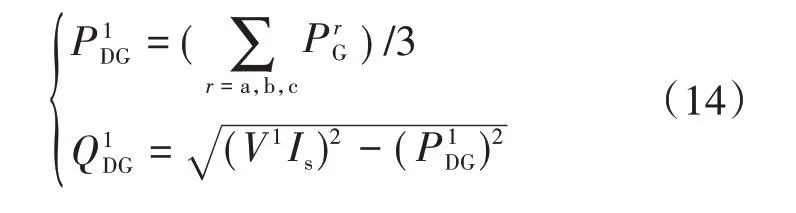
式中：Is为正序注入电流给定值。在动态潮流计算过程中，将式（12）—式（14）直接代入式（6）和式（7）中即可。

3 算法流程

基于序分量的主动配电网三相动态潮流算法可以实现三相解耦并行计算，其中正序系统采用牛顿-拉夫逊法进行迭代计算，负序和零序系统可以通过节点电压方程直接解算，从而大幅提高了计算效率，具体计算流程如图3 所示。首先，形成节点导纳矩阵，同时初始化各节点电压、功率、分担系数等初始变量，其次，计算出分担功率缺额后的分布式电源的出力，并判断节点电压是否越限，若越限，则调整松弛节点和分布式电源的分担系数，最后通过所得计算功率失配量和雅克比矩阵，求解系统各项参数，直至系统收敛。

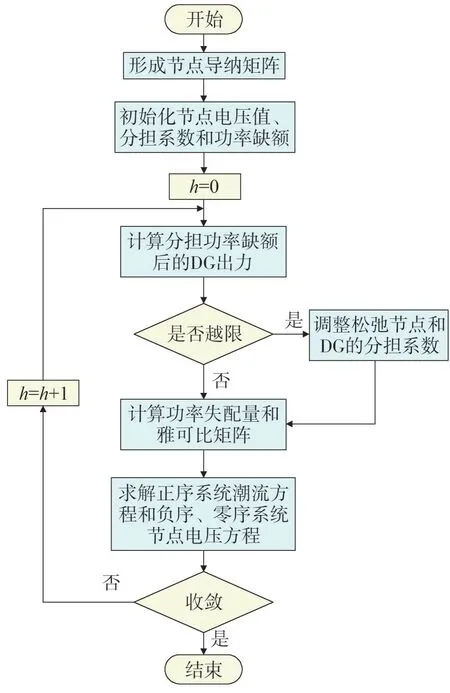
图3 基于序分量的主动配电网三相动态潮流算法流程

4 仿真算例

4.1 算例1

对蒙西某地区35 kV 配电网进行仿真，分析单DG 接入的情况。额济纳220 kV 变电站的低压节点为整个配电网的松弛节点，天风哈日布勒风电场为接入的分布式电源，如图4所示。

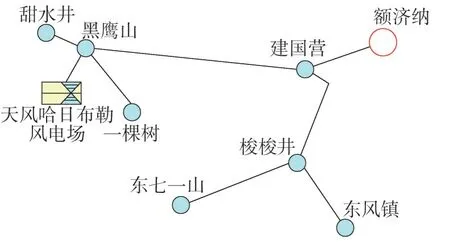
图4 蒙西某地区35 kV配电网

设定方案1 为基态负荷运行方式，DG 不参与分担功率缺额；方案2 相对基态运行方式负荷有所增加，DG不参与分担功率缺额；方案3研究负荷增加且DG参与分担功率缺额的情况。对3个方案进行仿真计算，结果如表1所示。

表1 3种方案计算结果

从表1 可以看出，相比于方案1 的计算结果，方案2 中系统负荷增加后，造成了网络损耗同步增加，同时DG 接入节点电压出现了下降；方案3 中，DG 参与分担功率缺额后，不仅降低了系统网损，而且提高了节点电压。

4.2 算例2

对IEEE33节点三相配电系统进行仿真，分析多种DG接入的情况。在系统中接入4台DG，如图5所示。电压基准值取为12.66 kV，功率基准值取为10 MW。

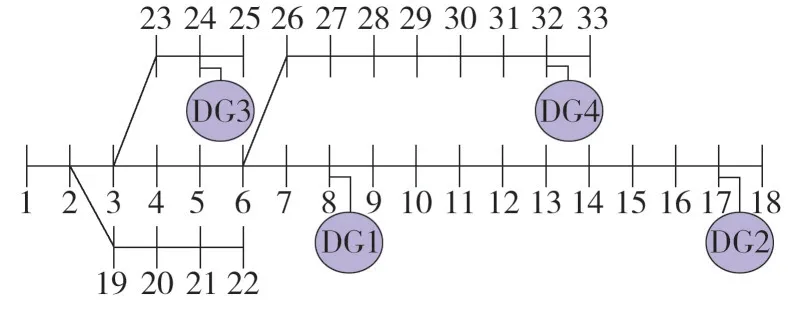
图5 多DG接入的IEEE33节点配电系统

DG 的类型、接入位置和参数如表2 所示。设定方案1 即为常规潮流计算方式，DG 不参与分担功率缺额；方案2—方案4 研究DG 参与分担功率缺额的情况，且DG 的功率缺额分担系数逐渐上升，同时按出力裕度的比例确定各DG 的分担系数，如表3所示。

表2 DG接入情况

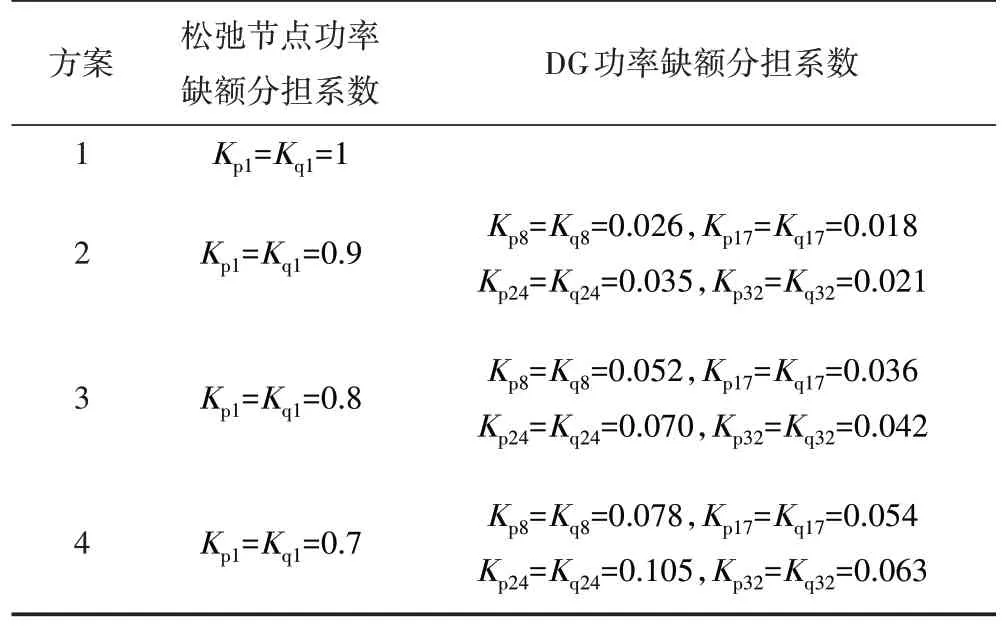
表3 4种方案参数设置

对4 种方案进行仿真分析，计算其系统松弛节点的出力、系统有功网损、节点电压水平，如图6—图8所示。

对比分析4 种方案的仿真计算结果，可以得出如下结论：

1）根据图6可知，DG分担系数的逐步增加，表明DG 在参与分担功率缺额中的作用越来越大；与此同时，松弛节点分担的功率越来越小，表明在动态潮流计算中，DG 参与分担功率不平衡量可以减轻松弛节点的分担压力，从而释放更多容量，保留足够裕度，以应对系统其他突发情况。

2）根据图7 可知，当DG 分担系数增加后，使DG的出力同步增加，即向系统注入了更多功率，对三相配电系统起到了功率补偿作用，从而降低了系统的网损。

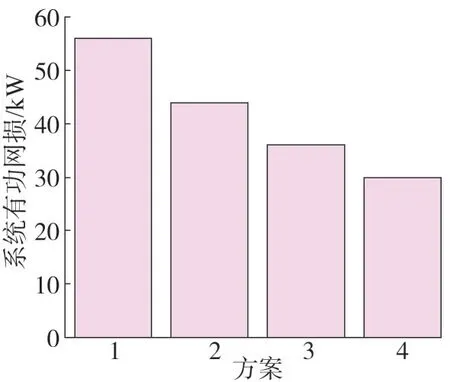
图7 4种方案中系统有功网损

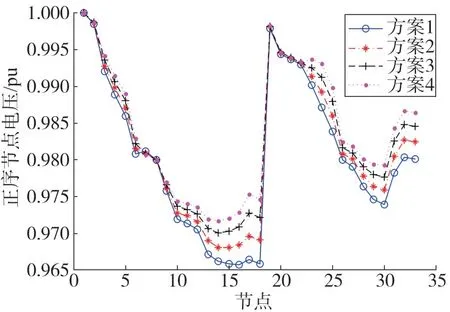
图8 4种方案中系统节点电压分布

3）根据图8可知，DG出力增加后，一方面降低了支路功率损耗，同时向接入节点注入了更多无功功率，从而对周围节点电压起到了支撑作用；当多DG接入时，便能够提升整个系统的电压水平。

需要指出的是，对于实际运行中的主动配电网，若DG本身无调节能力或调节能力有限，如果此时赋予DG 较大的功率缺额分担系数，以至于超出DG 的调节能力时，将对系统的频率稳定性造成影响。

5 结语

提出一种基于序分量的主动配电网三相动态潮流算法，通过定义功率缺额分担系数，使不同控制策略的DG能够参与分担系统的有功和无功功率缺额，并给出了DG出力越限后的处理方法，克服了传统常规潮流计算中全部功率缺额均由松弛节点承担的弊端，从而更好地模拟主动配电网实际运行情况。通过对蒙西某地区配电网和IEEE33 节点配电系统进行仿真，对比分析了多种不同方案，仿真结果表明DG 参与分担系统功率缺额后，能够减轻松弛节点的分担压力、降低网络损耗、提升系统电压水平。