融合拓扑势的有向社交网络关键节点识别模型

李 慧

(首都师范大学 教育学院，北京100048)

1 引 言

复杂网络系统的非同质拓扑结构，决定了网络中节点的重要度不同.与普通节点相比，复杂网络的重要节点对网络的结构与功能具有更明显的影响[1]，采用定量方法评估网络节点重要度、识别网络中的关键节点意义重大，已成为复杂网络理论研究的热点之一.作为典型的复杂网络，社交网络通常指以各种连接或相互作用的模式而存在的一组人或群体[2-5]，如朋友关系网络、科研合作网络、在线社交关系网络等，可以抽象为一个由节点(代表社会成员)和连边(代表节点间关系)构成的网络图.在社交网络中，每位社会成员扮演着不同的社会角色，反映了该用户与其邻居甚至与整个网络中所有用户之间的行为关系.识别用户角色尤其是关键节点对于用户行为预测、组织网络分析、舆情监测、网络营销等具有重要的理论意义和实用价值.

目前已提出许多复杂网络关键节点识别算法，基于网络拓扑结构的经典方法包括度中心性[6]、介数中心性[7]、接近中心性[8]、特征向量中心性[9]等.最直观最基本的方法是度中心性，其计算简单有效，但仅反映复杂网络的局部信息，没有考虑节点的自身特性和节点之间的相互影响[10].Chen等考虑节点及其邻居节点的度提出半局部中心性[11].介数中心性描述了节点对网络所传播信息流的控制能力，接近中心性描述了节点到达网络其他节点的快慢程度，二者考虑了网络的全局信息，但算法时间复杂度过高.特征向量中心性则以相邻节点的重要度作为衡量某节点重要度的指标.基于随机游走思想的关键节点识别算法主要包括PageRank算法[12]、LeaderRank算法[13]、HITS[14]等.PageRank算法假设节点具有相同的跳转概率，将PageRank值平均分配给相邻节点，存在排序结果不唯一的缺陷.LeaderRank算法很好地解决了上述问题，收敛性更好，鲁棒性更强，但标准的LeaderRank算法不能直接应用于加权网络[15].HITS算法采用节点的权威值和枢纽值综合评价节点的重要性.此外，还有基于节点移除的算法和基于D-S证据理论[16]的算法等，但算法时间复杂度高，在非连通网络中的识别效果不理想.

上述算法大多从网络拓扑结构的角度衡量节点重要度，忽略了每个节点的自身特性[17，18]和节点之间的相互影响.但Fowler和Christakis提出的三度影响力原则认为节点既对其直接相连的邻居节点产生直接影响，还对三度以内的邻居节点产生间接影响[19].因此，本文采用节点的有向拓扑势，综合考虑节点的属性以及节点与其近邻节点之间的相互影响力，提出一个新的节点重要度指标—拓扑势距离(Topological Potential Distance，TPD)，并将其应用于关键节点识别；进而提出了基于二维有向拓扑势的用户角色识别算法.在真实网络中的对比实验结果表明：与度中心性、介数中心性、接近中心性、PageRank、HITS等相比，拓扑势距离能有效识别有向加权网络中的关键节点，合理区分重要度相当的节点，并识别网络中的用户角色.

2 基本概念

2.1 节点拓扑势

根据有源物理场的思想，网络G=(V，E)可以看作一个包含n个节点及其相互作用的物理系统，每个节点周围存在一个拓扑场，对场中的所有节点产生一定的拓扑势，其拓扑势值随网络距离的增长而快速衰减[20].基于数据场理论提出的节点拓扑势，反映了节点受自身及其近邻节点共同影响的程度.

定义1.无向拓扑势.假设无向网络拓扑为G=(V，E)，V={v1，v2，…，vn}为节点的非空有限集，E⊆V×V为边的非空有限集，节点vi的拓扑势为：

(1)

其中，N为网络中的节点数|V|；mj≥0代表节点vj的质量，可映射为实际网络中的固有属性；dji表示节点vj到节点vi的最短路径长度；σ为影响因子，用于控制节点的影响范围，可根据节点拓扑势熵进行优选.

定义2.无向拓扑势熵.给定无向网络G=(V，E)及拓扑势场，其拓扑势熵为：

(2)

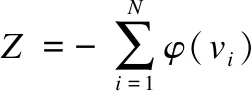
2.2 有向拓扑势

定义3.有向拓扑势.设有向加权网络G=(V，E，W)，V为节点集，E为有向边集，W为有向边的权重集合，节点vi的入度拓扑势φin(vi)和出度拓扑势φout(vi)分别定义为：

(3)

(4)

其中，dwji为在有向边的权重影响下节点间的最短距离，mj为节点vj的固有属性.在实际网络中，边权重越大表明节点间的联系越密切、距离越小.设节点vj到节点vi的最短路径为e1→e2→…→em，dr为第r段的距离长度，wr为对应边er的权重，则：

(5)

根据影响因子σ确定的影响范围l不再针对节点间的跳数而是针对dwji，即dwji≤l的节点都在影响范围之内.

在有向网络中，节点vi的入度拓扑势φin(vi)代表该节点受其他节点影响的程度，出度拓扑势φout(vi)则反映了节点vi对其他近邻节点的影响能力.

2.3 用户角色

用户角色是社交网络中用户行为和关系的划分，即对用户位置、用户行为或虚拟身份的刻画.如：在线社交网络中的不同用户拥有不同ID，每位用户的参与方式、互动行为和语言风格等迥然不同，决定了该用户的角色.本文把入度拓扑势和出度拓扑势作为用户角色识别的关键特征，建立二维拓扑势图(横坐标轴为入度拓扑势，纵坐标轴为出度拓扑势，如图1所示)，定义4类用户角色.①桥接用户：具有较大的入度拓扑势和出度拓扑势，在网络中具有承上启下的关键作用，位于图1的I区；②贡献用户：具有较大的出度拓扑势，主动与其他用户交互，对其近邻用户产生较大影响，位于图1的II区；③接收用户：具有较大的入度拓扑势，通常是网络中用户交互行为的被动接收者，易受其他用户的影响，位于图1的III区；④普通用户：出度拓扑势和入度拓外势均不显著，位于图1的IV区.

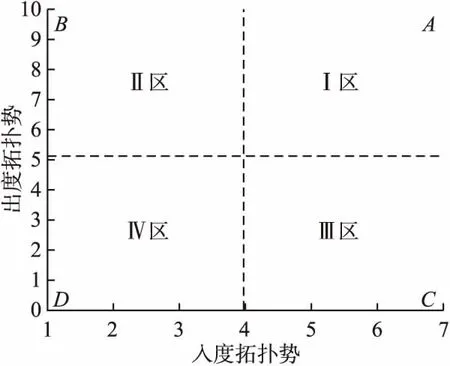
图1 二维拓扑势图Fig.1 2D topological potential distribution map

定义4.用户角色分布向量.给定有向加权网络G=(V，E，W)，节点vi从属于4类角色的概率定义为角色分布向量Pi=，其中分量pik为角色从属概率：

(6)

dik是节点vi到二维拓扑势图(如图1所示)中4个顶点A(maxφin，maxφout)、B(minφin，maxφout)、C(maxφin，minφout)和D(minφin，minφout)的欧式距离，minφin，minφout，maxφin，maxφout分别为网络中所有节点入度拓扑势和出度拓扑势的最小值和最大值.

在获得节点vi的角色分布向量Pi=后，比较角色从属概率pik的大小，选择概率最大的角色作为节点vi的角色.

定义5.拓扑势距离.在二维拓扑势图中，离顶点A距离越近的节点，在网络中发挥的作用越大，因此定义节点vi的拓扑势距离Ti为：

(7)

节点vi的拓扑势距离越小，离顶点A越近，其重要度越高；反之，节点的重要度越低.

3 算 法

本文针对有向社交网络，以入度拓扑势和出度拓扑势作为分析节点重要度及识别用户角色的主要特征，提出节点重要度的度量指标——拓扑势距离，根据节点的有向拓扑势及局部影响力将节点划分为4类角色.

3.1 基于有向拓扑势的关键节点识别

算法1.基于有向拓扑势的关键节点识别算法

输入：网络G=(V，E，W)，影响范围的增量Δl

输出：所有节点的拓扑势距离T及排名

1.初始化，l=0；

2.计算网络中所有节点对之间的最短距离，得到矩阵Q；

3.H=minH=log(N)；

4.whileH≤minHdo

5. minH=H；

6.l=l+Δl；

8. 根据l、σ分别计算所有节点的入度拓扑势和出度拓扑势；

9. 计算H，并保存l、σ和H；

10.endwhile

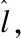
13.forvi∈Vdo

14. 计算节点vi的入度拓扑势φin(vi)和出度拓扑势φout(vi)；

15.endfor

16.forvi∈Vdo

17. 计算节点vi的拓扑势距离Ti；

18.endfor

19.根据拓扑势距离，对所有节点进行排序；

20.ReturnT、节点排名

3.2 基于二维拓扑势的用户角色识别

有向加权网络中，用户角色识别的基本思想为：计算节点vi的角色分布向量Pi=，其最大分量对应的角色就是节点vi的角色；根据各分量值的大小，判断节点vi隶属于该角色的程度.具体过程如算法2所示.

算法2.基于二维拓扑势的用户角色识别算法

输入：网络G=(V，E，W)中所有节点的入度拓扑势φin和出度拓扑势φout

输出：所有节点的角色分布向量P及对应的角色

1.根据φin和φout的最大值和最小值，得到二维拓扑势图的4个顶点；

2.forvi∈Vdo

3. 计算节点vi到4个顶点的欧式距离dik；

4.endfor

5.forvi∈Vdo

6. 计算vi的角色分布向量Pi=；

7.endfor

8.获得所有节点的所属角色及其程度；

9.ReturnP、用户角色及程度

4 实验与分析

4.1 实验数据

为了验证拓扑势距离在有向社交网络的用户角色识别和节点重要度评估的效果，本文针对3个不同规模、不同类型的真实网络数据集Strike、Polblogs和豆瓣话题回复网络设计对比实验.

Strike是由24个节点和38条边组成的有向网络[21]，节点代表一家木材加工厂的工人，有向边表示工人之间的联系，边权值均为1.Strike网络描述了一场罢工运动中工人之间的沟通情况，说西班牙语的工人和说英语的工人之间的沟通较少；在说西班牙语的工人中，Alejandro最精通英语；Bob会讲西班牙语，与Norm关系密切；Ozzie是Karl的父亲.

Polblogs[22]是2004年美国大选期间美国政治博客之间的超链接形成的有向网络(1490个节点和19090条有向边)，以不同的政治博客为节点，每个节点具有1个表示其政治倾向的属性(即民主党或共和党)；各博客之间的超链接为有向边，边权值均为1.主要拓扑参数为：平均度12.768、网络直径9、聚类系数0.172、平均路径长度3.39.

豆瓣话题回复网络来源于采用网络爬虫自主下载的豆瓣网人文经典阅读小组2014年2月-2016年5月的话题回复数据，以用户为节点、用户之间的话题回复关系为有向边、回复次数为边权，构建而成的有向加权网络(有6260个节点和16833条有向边).主要拓扑参数为：平均度3.862、网络直径11、聚类系数0.113、平均路径长度3.709.

4.2 用户角色识别结果分析

选取7种经典的节点重要度指标：①中心性指标，包括加权度、介数中心性、接近中心性、特征向量中心性；②链接分析法，包括PageRank、HITS-Authority、HITS-Hub，实现拓扑势距离与7项指标的对比分析.表1-表3分别列出了在3个真实网络上不同方法得到的前10/15个重要节点，表中括号前数值为节点编号，括号内为对应方法计算所得的数值(即节点排序的依据).

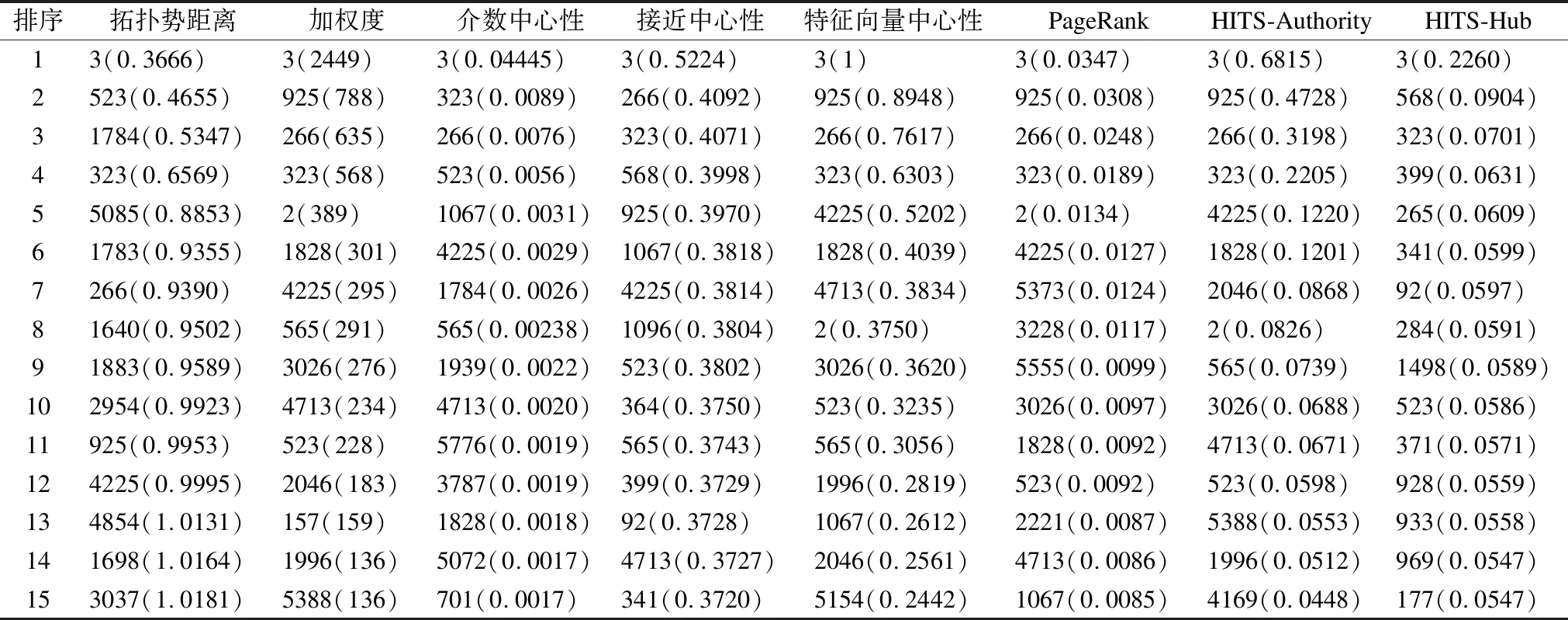
表3 豆瓣话题回复网络中节点重要度排序结果Table 3 Ranking results of user influence in DouBan reply network

4.2.1 Strike网络的用户角色识别结果

表1列出了Strike网络在8项指标上的节点重要度排序结果，可以看出：拓扑势距离排名前5的节点，被其他重要度指标认可；例如，拓扑势距离排名第1的节点7(Bob)，被其余5项指标选为第1名；拓扑势距离排名第2的节点12(Norm)，被其余4项指标选为第2名.与加权度、接近中心性、PageRank、HITS-Authority、HITS-Hub相比，拓扑势距离的精度更高，如节点2、节点11、节点18和节点19的加权度值相同，并列第4，而拓扑势距离无并列排名、区分度高.

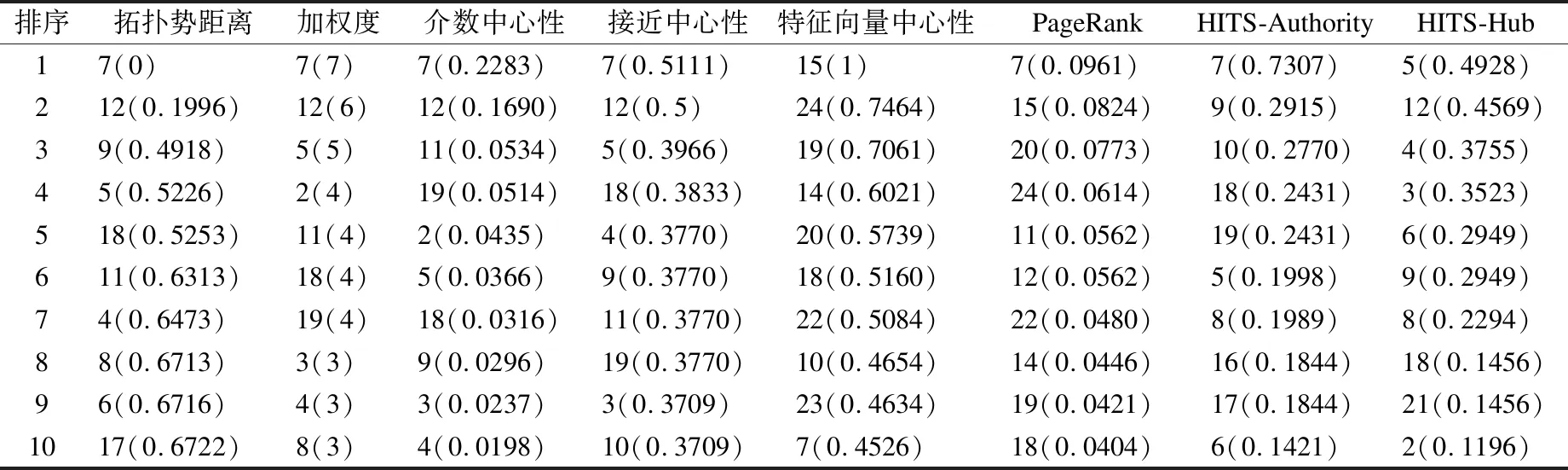
表1 Strike网络中节点重要度排序结果Table 1 Ranking results of user influence in Strike network

图2是Strike网络的二维拓扑势图，可以看出：节点7(Bob)和节点12(Norm)属于“桥接用户”，具有较大的入度拓扑势和出度拓扑势.其中，节点7(Bob)的有向拓扑势最高，是罢工运动中的领导、核心；节点12(Norm)的入度拓扑势和出度拓扑势均不突出，但在图2中能清晰表明该节点的重要程度.入度拓扑势大、出度拓扑势小的“接收用户”，在网络中人数最多，通常是听从指挥的人员，例如节点15(Domingo)从不联系别人、只有别人联系他.仅出度拓扑势相对较大的“贡献用户”，对其近邻节点具有较大的影响力.入度拓扑势和出度拓扑势均较小的“普通用户”，如节点21(Quint)，在罢工运动中的作用相对较小.入度拓扑势或出度拓扑势最小的节点，处于罢工网络的边缘，如节点1(Frank)、节点24(Wendle)等.

图2 Strike网络的二维拓扑势图Fig.2 2D topological potential distribution map of Strike network

根据Strike 网络的用户角色识别结果，得出结论：从二维拓扑势图中能有效识别4类用户角色，进而判断不同用户在网络中的作用；本文提出的拓扑势距离能反映用户的影响力(即节点重要性).

4.2.2 Polblogs网络的用户角色识别结果

表2列出了Polblogs网络在8项指标上的节点重要度排序结果，可以看出：拓扑势距离排名前5的节点，被其他重要度指标认可；例如，拓扑势距离排名第1的节点855，被其余2项指标选为第1名；拓扑势距离排名第3的节点55，被其余7项指标选为前10名.与介数中心性相比，拓扑势距离的精度更高，如节点1000和节点1153的介数中心性相同，并列第12，而拓扑势距离无并列排名、区分度高.

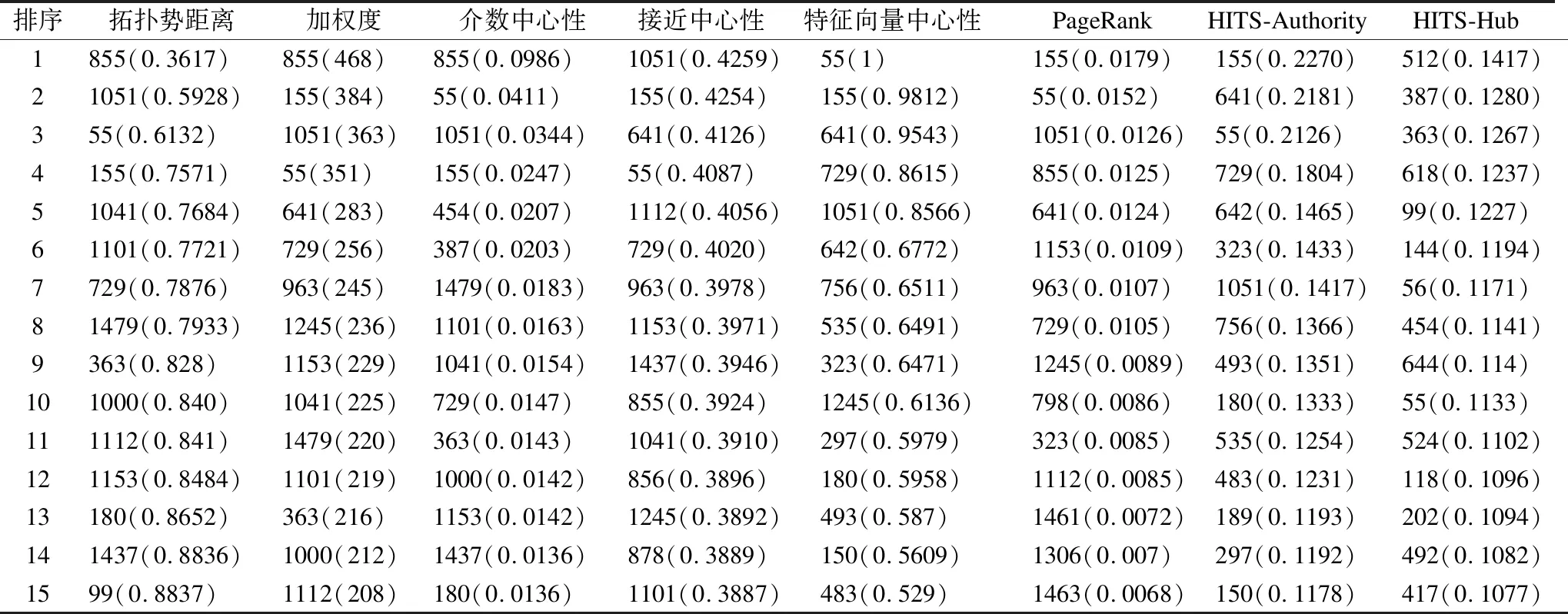
表2 Polblogs网络中节点重要度排序结果Table 2 Ranking results of user influence in Polblogs network

图3是Polblogs网络的二维拓扑势图，可以看出：节点855属于“桥接用户”，具有较大的入度拓扑势和最大的出度拓扑势，是拥有超链接数最多的政治博客，属于Polblogs网络中承上启下的核心节点.入度拓扑势大、出度拓扑势小的“接收用户”有12个，出度拓扑势大、入度拓扑势小的“贡献用户”有9个，其中拓扑势距离排名第2-15位的节点中有11个属于典型的“接收用户”或“贡献用户”.入度拓扑势和出度拓扑势均较小的“普通用户”，在网络中占比最大，其作用相对较小.

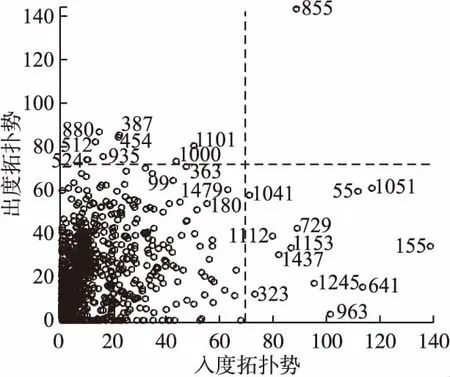
图3 Polblogs网络的二维拓扑势图Fig.3 2D topological potential distribution map of Polblogs network

4.2.3 豆瓣话题回复网络的用户角色识别结果

表3列出了豆瓣话题回复网络在8项指标上的节点重要度排序结果，可以看出：入度拓扑势和出度拓扑势排名前5的节点，被其他重要度指标认可；例如，出度拓扑势排名第1的节点3，被其余7项指标均列为第1名.与加权度、介数中心性、PageRank、HITS-Hub相比，拓扑势距离的精度更高，如节点5776和节点3787的介数中心性相同，并列第11，而拓扑势距离无并列排名、区分度高.

由豆瓣话题回复网络的二维拓扑势图(如图4所示)可以看出：网络中绝大多数节点的入度拓扑势和出度拓扑势均较小，约98.43%的用户属于“普通用户”.节点3、节点523和节点1784是“桥接用户”；其中，节点3是管理员，经常发表新话题和回复别人的话题，共发表1116个新话题，回复1775个话题；节点523和节点1784各发表了198个、101个新话题，经常回复其他用户的话题，在网络中活跃程度较高，与其他用户互动频繁，具有相对较大的入度拓扑势和出度拓扑势，虽然有向拓扑势排名不突出，但在网络中具有重要的桥接作用.35个“贡献用户”的出度拓扑势较高，在网络中属于经常回复话题的用户；例如节点1714是管理员，回复的话题数较多，没有发表过新话题.60个“接收用户”的入度拓扑势较高；其中，节点925的入度拓扑势最高，发表131个新话题并被其他用户多次回复，但只回复过2个话题；节点1939是组长，其入度拓扑势高于出度拓扑势，发表85个新话题，回复30个话题；节点364、节点1828是管理员，经常发表新话题并被其他用户多次回复，但很少回复其他用户的话题.

图4 豆瓣话题回复网络的二维拓扑势图Fig.4 2D topological potential distribution map of DouBan reply network

结合实际数据背景，进一步分析：本文提出的用户角色识别模型找出了豆瓣话题回复网络中1.57%的重要成员，其中包括1名组长和8名管理员.管理员在豆瓣话题小组中的作用很多，如管理版务、引导话题导向、贡献原创资源、调节纷争等.1.57%的重要成员中有些用户是豆瓣话题小组中的普通成员，但却是领袖人物或某领域的专家，其“发帖数”、“回复帖数”、“被回复帖数”、“参与话题数”等均高于平均水平，体现了他们在论坛中的活跃程度，表明他们是论坛中的代表性用户.

综上所述，结论如下：拓扑势距离越小的节点，与二维拓扑势图的顶点A(maxφin，maxφout)距离越近，在网络中发挥的作用越大，如Strike网络中的节点7是罢工运动中的领导、核心，Polblogs网络中的节点855是拥有超链接数最多的政治博客，豆瓣话题回复网络中的节点3是管理员.入度拓扑势或出度拓扑势最小的节点，处于网络的边缘.拓扑势距离在节点重要度评估上的区分度最好，主要体现在表1-表3中仅有拓扑势距离指标没有出现并列排名的情况，其区分度明显优于其他7项指标.从计算复杂度来看，拓扑势距离比加权度高，比介数中心性低，与其他5项指标基本相当.

4.3 拓扑势距离与其他节点重要度指标间的关系

拓扑势距离能实现对有向加权社交网络的所有用户进行重要性评价，拓扑势距离值越小的用户越重要、排名越靠前.为验证拓扑势距离识别有向加权社交网络中关键节点的合理性，分别对3个真实网络数据集中节点的加权度、介数中心性、接近中心性、特征向量中心性、PageRank值、HITS-Authority值、HITS-Hub值和拓扑势距离进行相关分析，如图5所示.

在统计学中，Kendall等级相关系数τ[23]常用于度量两种排序结果相关性的强弱.τ的取值范围为[-1，1]，τ=1表明两种排序的等级相关性一致，τ=-1表明两种排序的等级相关性完全相反；τ=0表明两种排序相互独立.Kendall等级相关系数τ有三种计算方式：τA、τB和τC.由于不同社交网络用户可能拥有相同的拓扑势距离值或中心性指标值(即等级相同)，本文采用τB度量拓扑势距离与其他7项指标排序结果的相关性强弱，结果见表4.

表4 拓扑势距离与7项指标之间的τBTable 4 τB between topological potential distance and 7 indexes

假设两个n维随机变量X、Y的第i(1≤i≤n)个元素分别表示为Xi、Yi，X和Y对应元素组成的元素对集合为XY.当XY中任意两个元素(Xi，Yi)与(Xj，Yj)的排名相同，即满足Xi>Xj且Yi>Yj或满足XiXj且YiYj时，认为二者不一致.当出现Xi=Xj或Yi=Yj时，认为二者既非一致也非不一致.定义τB如下：

(8)

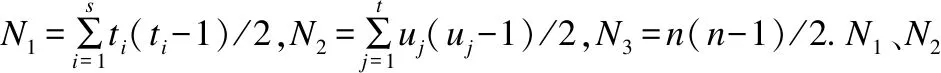
图5是拓扑势距离与7项指标(加权度、介数中心性、接近中心性、特征向量中心性、PageRank、HITS-Authority、HITS-Hub)分别在Strike、Polblogs和豆瓣话题回复网络中用户重要

图5 拓扑势距离与7项指标的关系图Fig.5 Relation between topological potential distance and 7 indexes

性排序间的关系图，显然拓扑势距离与7项指标均呈现明显的负相关性.使用τB度量拓扑势距离与7项指标排序结果的相关性，见表4.在Polblogs网络和豆瓣话题回复网络中，拓扑势距离与7项指标间具有显著性水平0.01的强负相关性；在Strike网络中，拓扑势距离与特征向量中心性、HITS-Authority间具有显著性水平0.05的强负相关性，与其他5项指标间具有显著性水平0.01的强负相关性.表明拓扑势距离在3个有向社交网络中识别出的关键节点具有合理性.

4.4 节点重要度评估结果分析

4.4.1 评价标准

基于网络鲁棒性与脆弱性分析，评估节点重要度排序算法.采用极大连通系数G与网络效率下降比例μ作为评估指标，计算移除特定用户前后网络结构的变化，进而评价相对应节点的结构重要性.

根据节点重要度排序算法的结果，按顺序对所有节点排序，移除一部分重要节点，计算网络的极大连通系数G，并判断移除节点后网络极大连通子集[24]的变化.

G=R/N

(9)

其中，N为网络的节点总数，R为移除一部分重要节点后极大连通子集的节点数.极大连通系数G∈[0，1]；G取值越大，表明网络的拓扑连接越强；随着节点的删除，极大连通子集的规模逐渐变小，极大连通系数G随之减小，网络的拓扑连接减弱；G变小的趋势越明显，攻击网络的效果越好；当G=0时，网络中将不存在极大连通子集.

网络效率E[25]定义为：

(10)

其中，εij=1/dij，dij为节点vi和节点vj之间的最短路径，N为网络的节点总数.网络效率E能有效度量网络的连通性，E取值越大，表明网络的连通性越强；当移除特定节点时，网络中有些路径被中断，某些节点对之间的最短路径变大，导致网络的平均路径长度增大，网络的连通性变弱；E下降的趋势越明显，表明模拟攻击的效果越好.

网络效率下降比例μ为：

μ=1-E/E0

(11)

其中，E为节点移除后的网络效率，E0为原始网络的网络效率.μ∈[0，1]，μ取值越大，表明移除节点后的网络效率越差.本文通过删除网络中的特定重要节点，计算遭受攻击前后的网络效率下降比例，并以此衡量各节点的重要度.

4.4.2 动态攻击结果

针对3个真实网络，根据拓扑势距离、加权度、介数中心性、接近中心性、特征向量中心性、PageRank、HITS-Authority、HITS-Hub的排序结果，分别删除网络中一定比例排序靠前的节点，模拟网络遭受动态攻击时极大连通系数G与网络效率下降比例μ的变化(如图6、图7所示)，进而评价节点重要度指标的准确性.当网络遭受动态攻击时，由于移除节点后网络拓扑结构发生变化，因此必须重新计算各个节点的8项指标值并排序，然后按照节点的重要度依次删除节点.

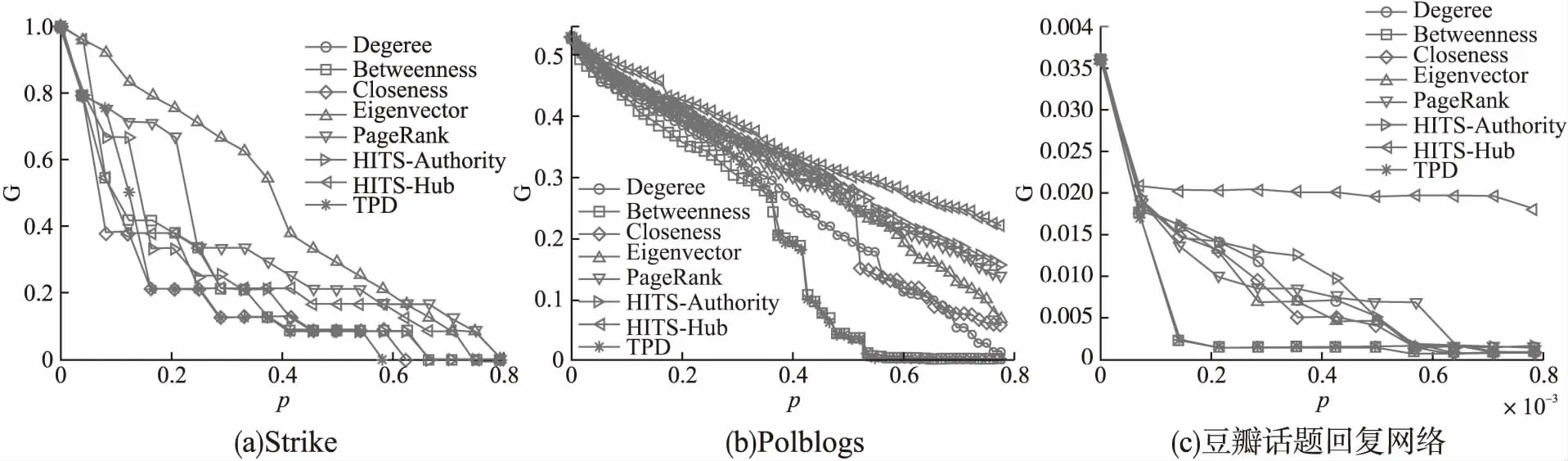
图6 利用不同指标动态删除一定比例排序靠前的节点后极大连通系数G的变化Fig.6 Relation between relative size of giant component G and a certain proportion of key nodes dynamically removed from networks

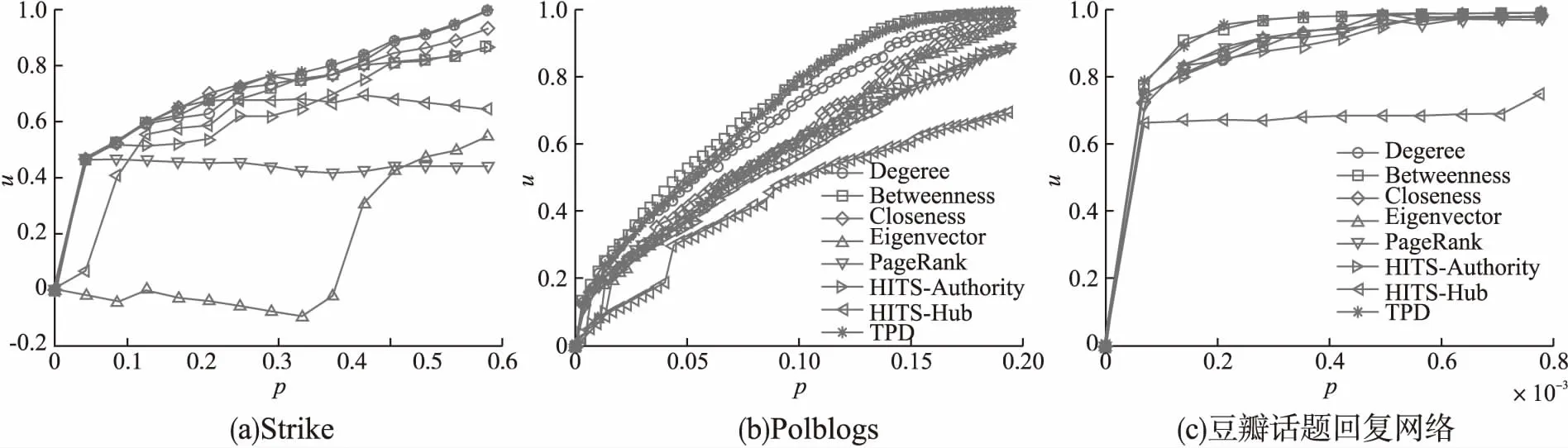
图7 利用不同指标动态删除一定比例排序靠前的节点后网络效率下降比例μ的变化Fig.7 Relation between decline rate of network efficiency μ and a certain proportion of key nodes dynamically removed from networks

如图6所示，动态删除3个网络中排序靠前的节点时，拓扑势距离指标导致网络极大连通系数G变小的趋势最明显.尤其在豆瓣话题回复网络(图6(c))中，拓扑势距离指标在动态攻击的初始阶段表现出比其他7项指标更好的攻击效果，在整个模拟动态攻击过程中对网络结构的破坏性最强；而HITS-Hub指标的动态攻击效果最差，曲线中出现网络极大连通系数G不随节点移除而下降的情况.在Strike网络(图6(a))和Polblogs网络(图6(b))中，虽然拓扑势距离指标在动态攻击的初始阶段表现稍差，但当分别选择性删除排名前16%和9%以上的节点时，拓扑势距离指标使得网络极大连通系数G最小，动态攻击最突出.

由图7(a)可知，在Strike网络中，采用拓扑势距离指标删除排序靠前的节点导致网络效率下降比例μ最大，网络碎片化效果最突出，动态攻击效果最佳，当动态删除到第14个节点时μ为最大值1；采用特征向量中心性、PageRank、HITS-Authority、HITS-Hub等指标动态删除节点时，出现了网络效率下降比例μ局部下降的情况，表明这些指标排名靠前的节点并不是当前网络的核心节点，难以有效评价Strike网络的节点重要度.由图7(b)可知，在Polblogs网络中，选择性删除8项指标中前9%的节点时，介数中心性指标对网络的破坏效果略优于拓扑势距离；但选择性删除前10%以上节点时，拓扑势距离指标使网络效率E下降的幅度最大，对网络的瓦解效果最明显.由图7(c)可知，采用8项指标动态攻击豆瓣话题回复网络时，拓扑势距离指标使网络效率下降比例μ最大，删除排序靠前的节点后导致网络的连通性最差；HITS-Hub指标的动态攻击效果最差，曲线中出现了网络效率下降比例μ不随节点移除而上升的情况，表明这些HITS-Hub排名靠前的节点不是当前网络的核心节点，难以有效衡量豆瓣话题回复网络的节点重要性.

综合来看，移除重要节点后网络的连通性越差，极大连通系数G变小的趋势越突出，网络效率E的下降趋势越明显，网络效率下降比例μ的上升趋势越显著.在3个真实有向社交网络中，与其他7项指标相比，拓扑势距离度量节点重要度的效果最好、最稳定，没有出现随着节点删除比例的增加网络效率下降比例μ下降的现象.

5 结 论

关键节点识别是社交网络研究中的重要研究问题之一，对研究社交网络的结构和功能、分析用户之间的交互过程、预测用户行为、监测网络舆情等具有重要意义.通过用户角色辨识网络中的关键用户有助于改进网络防护策略，提升高影响力用户的安全防护能力，进而提高网络拓扑结构的稳定性.本文针对有向社交网络中节点重要度分析和用户角色发现，提出一个新的节点重要度指标——拓扑势距离，能有效辨识网络中的关键节点；提出一种基于二维有向拓扑势的用户角色识别模型，根据节点的有向拓扑势及局部影响力划分4类用户角色.真实社交网络的对比实验结果表明：二维有向拓扑势图能清晰直观地刻画有向加权社交网络中的4类用户角色，拓扑势距离越小的用户在网络中发挥的作用越大；拓扑势距离与7项节点重要度指标(加权度、介数中心性、接近中心性、特征向量中心性、PageRank、HITS-Authority、HITS-Hub)间具有明显的强负相关性；与7项指标相比，拓扑势距离在节点重要度评估上的区分度最好，当网络遭受动态攻击时，拓扑势距离使网络碎片化程度最高、动态攻击效果最好.下一步工作将拓展本文模型至动态网络中，致力于动态网络的关键节点识别和演化研究.