一种AGV故障诊断方法

刘传家，赵常均，王远航，林贞琼

（1.工业和信息化部电子第五研究所，广东 广州 511370；2.广州智能装备研究院有限公司，广东 广州 510700）

0 引言

随着企业物流运输系统对运行成本、柔性化和信息化等方面的需求，自动导引车（AGV）在物流自动化运输领域中的应用越来越广泛[1]。在实际生产中，作为物料运输工作的主要执行者，如果AGV故障的检测不准确、处理不及时，整个运输系统将工作在无法预测的方式下，轻则影响生产效率，重则给企业造成重大安全事故及财产损失。因此，对AGV故障诊断方法的研究具有重要的实际应用价值。随着AGV故障诊断应用需求的日益提升，部分学者针对相关故障特征提取及诊断方法开展了研究[2-6]。在上述基础上，本文以轮式AGV为研究对象，主要研究了基于卡尔曼滤波的残差预测及故障特征提取方法，以及基于BP神经网络的故障诊断方法。同时，对上述研究进行拓展，提出了一种基于混合粒子群算法的BP神经网络参数优化方法和一套完整的AGV故障诊断方法。

1 算法设计

轮式AGV的主要故障可分为机械故障和传感器故障两类，每一类包括多种具体的故障形式。本文仅针对上述两类中的部分故障形式进行研究，其中，机械故障主要指左、右驱动轮打滑；传感器故障主要指陀螺仪故障。定义故障类型为F1-F4，分别对应正常状态、左侧车轮打滑、右侧车轮打滑和陀螺仪故障4种状态。

1.1 AGV故障特征提取

本文的主要研究对象是轮式AGV，该AGV具有2个驱动轮和4个从动轮，配有2个编码器和1个陀螺仪。AGV的运动学模型如图1所示。

图1 轮式AGV运动学模型

根据图1，上述AGV的运动学模型可以表示如下：

式（1）中：θ——AGV中轴线与x轴的夹角；

θ˙——AGV偏航率；

υL——左轮速度；

υR——右轮速度；

L——驱动轮之间的距离；

V——AGV速度。

根据AGV运动学模型，为通过卡尔曼滤波器计算残差，建立AGV的状态方程如下：

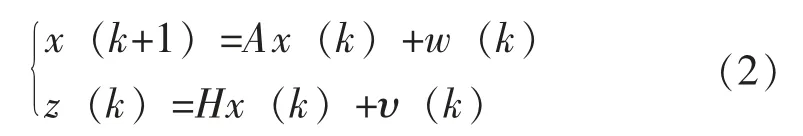
式（2）中：x——系统状态，x=[υLυRθ˙]T；

z——系统观测，z=[υLυRθ˙]T；

w（k）——过程噪声；

υ（k）——测量噪声。

卡尔曼滤波器的迭代方程如下：

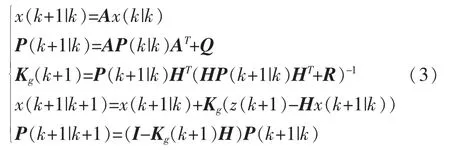
式（3）中：A——系统状态矩阵；

P——状态估计协方差矩阵；

K g——卡尔曼滤波器增益矩阵；

Q——过程噪声协方差矩阵；

R——测量噪声协方差矩阵；

H——观测矩阵；

I——单位矩阵。

系统状态矩阵A和观测矩阵H需要根据所建立的故障模型来定义。对于AGV一侧轮胎打滑，可以认为在运动模型中对应侧的速度对于偏航率不起作用，即对应侧的速度为零。对于陀螺仪故障，可以认为偏航率不再受左、右轮速度的影响。基于上述分析，给出部分故障模型下的A阵及H阵值示例：正常状态时，左侧轮胎发生打滑故障时，A=

式（4）中：r——卡尔曼滤波器预测残差；

1.2 神经网络设计及参数优化

结合BP神经网络预测精度高及应用广泛等特点，本文采用BP神经网络进行故障诊断处理[8-9]。网络设计为包含输入层、隐含层和输出层的3层网络结构，其中输入、输出层各包含4个神经元节点，隐含层包含9个神经元节点。为了提高BP神经网络的收敛速度[10]，避免陷入局部最小值，采用标准粒子群与遗传算法相结合的混合粒子群算法对网络最优参数进行估计。混合算法摒弃了传统粒子群算法中通过跟踪极值来更新粒子位置的方法，引入遗传算法中的交叉和变异操作，通过粒子同个体极值和群体极值的交叉，以及粒子自身的变异的方式搜索最优解，可以有效地改善标准粒子群算法存在的局部最优解问题。算法的具体设计如下。

a）个体编码

粒子个体编码采用实数编码的方式，编码长度根据BP神经网络结构设置为85，初始时每个粒子随机生成。

b）适应度函数

为了使BP神经网络预测值与期望值的残差尽量小，选择样本预测值与期望值的欧氏距离之和作为适应度函数。

c）交叉操作

个体通过和个体极值、群体极值交叉进行更新，这里极值即最优解。首先，在个体长度范围内随机产生一个区间，个体将上述区间内的编码与极值对应区间内的编码执行交叉操作。对上述交叉操作得到的新个体采用优秀个体保留策略，即当新粒子的适应度优于旧粒子时才更新粒子个体。设第i个粒子个体为ai，极值粒子为ao，则两个粒子个体在第j位编码的交叉操作如下所示：

式（5）中：a′ij——新个体第j位编码的值；

b——[0，1]区间的随机数。

d）变异操作

在粒子个体长度范围内随机生成4个位置，然后分别针对这4个位置执行变异操作。与交叉操作类似，在变异操作中仍然采用优秀个体保留策略。第i个粒子个体中第j位编码的具体变异操作如下所示：

式（6）中：amax——aij的取值上界；

amin——aij的取值下界；

g——当前迭代次数；

G——最大迭代次数；

k、r——[0，1]区间的随机数。

基于上述（1）-（4）的设计，利用混合粒子群算法优化BP神经网络参数的具体过程如图2所示。

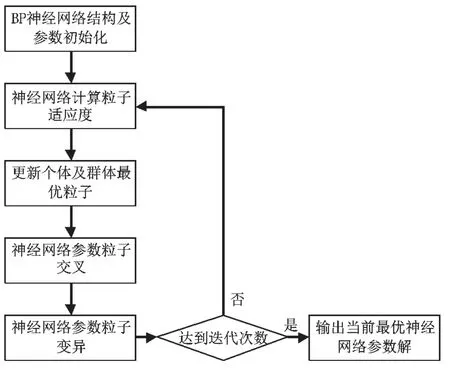
图2 基于混合粒子群的BP神经网络参数优化流程

1.3 故障诊断方法设计

本文设计的基于故障特征和BP神经网络的AGV故障诊断方法的基本框架如图3所示。

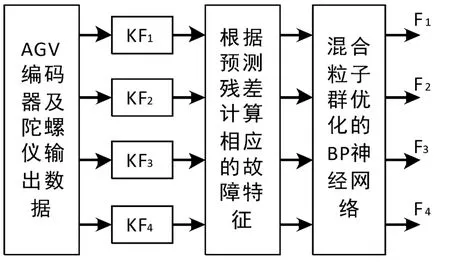
图3 AGV故障诊断方法框架

在图3中，KF1-KF4分别为针对F1-F44个故障状态设计的卡尔曼滤波器，具体的故障诊断方法流程如下：

a）分别获取左、右驱动轮编码器及陀螺仪传感器输出数据；

b）将上述数据分别输入到KF1-KF44个卡尔曼滤波器中，每个滤波器都产生一组对应的残差矩阵；

c）计算每个残差矩阵对应的马氏距离，分别对这些数据进行归一化处理，将处理后的数据作为AGV的故障特征；

d）采集多组数据分别按照步骤a）-c）提取故障特征并对这些故障特征数据进行手动标定，利用标定后的数据对基于混合粒子群优化的BP神经网络进行训练；

e）利用训练好的BP神经网络模型实现轮式AGV的故障诊断工作，给出最终诊断结果。

2 仿真与实验

AGV故障诊断实验主要包括独立实验和统计实验两个部分：在独立实验中，令AGV分别在正常和故障状态下运行，采集5组数据并进行在线分析诊断；在统计实验中，对100组数据进行离线仿真分析，进行两次实验，每次随机分配50组数据，统计故障诊断情况。下面首先给出独立实验的测试结果，具体如表1所示。

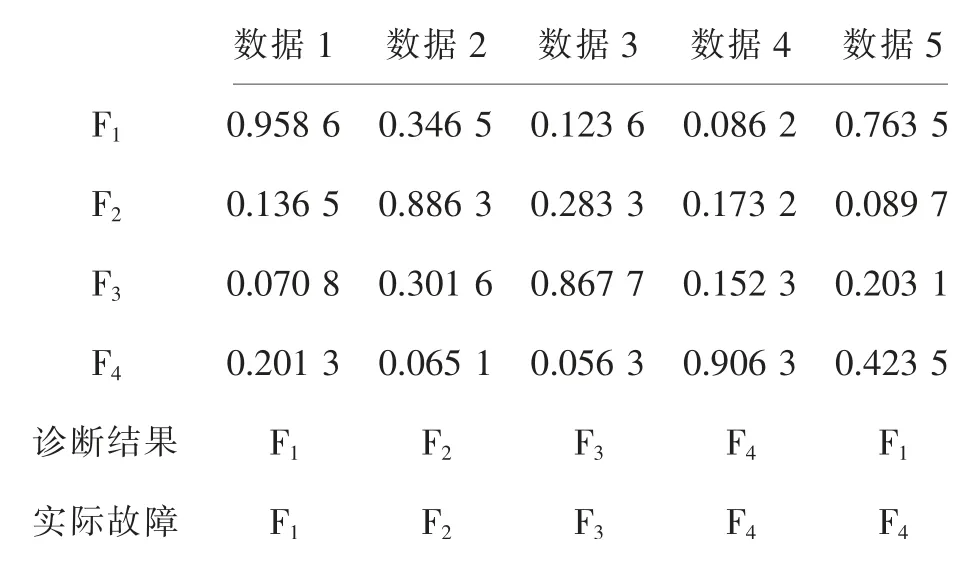
表1 独立实验结果

基于表1可以得出如下结论。

a）本文设计的故障诊断方法基本能够完成AGV车轮打滑及陀螺仪的故障诊断，方法的有效性可以得到初步验证。

b）对于陀螺仪的故障诊断出现了漏诊现象，即将陀螺仪故障诊断为正常状态，出现上述问题的主要原因是由于AGV在进行较长时间的直线运动时其陀螺仪输出会保持一定的数值不变，或在较小的范围内变化，如果此时AGV的陀螺仪传感器损坏并且也表现为输出数据不变，则故障诊断算法难以及时发现，因此出现了表1所示的漏诊现象。

统计实验结果如图4所示。

图4 AGV故障诊断统计实验结果

从图4中可以看出，在两次各50组数据的统计测试实验中，本文设计的故障诊断方法均可以达到85%以上的诊断准确率，该实验结果在独立实验的基础上进一步地验证了AGV故障诊断方法的有效性。

3 结束语

本文主要研究设计了一种AGV故障诊断方法，主要实现步骤如下：1）采集AGV编码器及陀螺仪输出数据，利用卡尔曼滤波器计算预测残差，然后计算残差对应的马氏距离作为故障特征；2）利用混合粒子群算法优化BP神经网络的初始权值及阈值，通过优化后的神经网络根据故障特征输入数据完成故障诊断。最后，通过实验测试验证了本文中所提出的方法的有效性。