大型邮轮大跨度开孔高腹板板架声振特性分析

喻 敏 陈梓恒 吴卫国

(武汉理工大学交通学院1) 武汉 430063) (武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心2) 武汉 430063)

0 引 言

开孔板结构一直是船舶与海洋工程领域的热门研究对象，国内外专家学者对此类结构的声振特性已经进行了广泛而深入的研究，他们运用不同的方法分析了矩形或圆形开孔板结构的声振特性问题[1].Cho等[2]运用假设模态法，Kwa等[3]运用独立坐标耦合法研究了矩形开孔板结构的振动特性.为了得到有椭圆内边界的矩形板的固有频率，Nogavg[4]通过实际模型试验对这种类型的开孔板结构进行了研究.Cho等[5]则运用有限差分法研究了矩形开孔板结构的动力学特性.有限元法在解决结构振动问题时，具有计算速度快，计算精度高，求解问题简单等优势，而在解决结构声辐射问题时，不能很好的处理无限域这一声辐射计算的前提条件，只能计算有限域的辐射声场将导致其辐射声场计算的误差很大；边界元法则能模拟无限域问题，能够弥补有限元法这一缺陷.因此，形成了相对比较成熟的有限元结合边界元分析方法，在Donaldson等[6]对结构固有频率和振型的理论推导的基础上,Zhong等[7]运用等几何法研究了含有大量开孔和不同形状FGM板结构的振动特性，陈美霞[8]运用边界元方法研究了普通平板结构的声辐射特性问题，Zhang等[9]运用FEM/BEM法研究了任意厚度各向同性板的振动与声辐射特性，并与解析结果进行比对，验证了此方法的准确性.

尽管对常规开孔板结构的声振特性有着广泛而深入的研究，但是针对大型邮轮上应用的大跨度开孔高腹板板架这类特殊结构的声振特性研究目前相对较少.文中以邮轮大跨度开孔高腹板板架结构为研究对象，运用有限元与边界元方法研究探索结构参数、边界条件、外部激励等因素对大跨度开孔高腹板板架结构声振特性的影响.

1 有限元理论分析

在有限元方法中，通常将连续的结构体离散为一个个单元，单元与单元之间通过节点相互连接，计算所需要的数据包含在节点上.

系统的整体有限元方程，即

(1)

式中：M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；Ft为系统节点荷载向量.

在经典无阻尼自由振动情况下，系统的整体有限元方程退化为

(2)

其振动形式为自由振动，该方程的解的形式为

(3)

式中：ω为常数.将解代入退化后的方程里，可得

(4)

消去eiω t，有

(5)

该方程有非零解的条件是系数行列式为零，即

|(K-ω2M)|=0

(6)

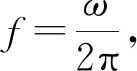
对于经典的板结构，运用瑞利积分，有

p=Zvn

(7)

式中：Z为声阻抗矩阵；p为表面声压矩阵；vn为法向振速矩阵.

结构法向振速与结构有限元节点振速的联系为

vn=Gv

(8)

式中：G为对应的变换矩阵.

有限元法作为目前为止研究结构振动最为行之有效的数值计算方法，可以求解出结构振速与外部载荷的关系.

[(-ω2M+iωC+K)/iω]v=f

(9)

式中：M,C,K分别为结构质量矩阵、阻尼矩阵、刚度矩阵.为了更加直接表示振速和外部载荷的关系，式(9)可变式为

v=[(-ω2M+iωC+K)/iω]-1f

(10)

故：

v=GQf

(11)

由以上分析可知，结构辐射声功率级的二次型矩阵式为

(12)

2 大跨度开孔高腹板架声振特性分析

2.1 有限元模型的建立

根据邮轮大跨度开孔高腹板板架结构特点，选择一典型板架结构为研究对象，计算模型见图1，骨材规格见表1.

表1 大跨度开孔高腹板结构参数

材料属性 板架材料均为钢材，其中甲板板、纵骨、纵桁材料为Q355钢材，密度为7.85×10-9t/mm3，弹性模量E=2.06×105MPa，泊松比为0.3；强横梁材料为Q235钢材，密度为7.85×10-9t/mm3，弹性模量E=2.06×105MPa，泊松比为0.3.其中纵向骨材连续，横向骨材断开.

2.2 结构参数对结构声振特性影响分析

2.2.1典型加筋板与本文结构声振特性对比分析

分别对不同的模型进行有限元前处理，采用SHELL单元进行网格划分，对其进行模态分析，分析结果见图2.

图2 开孔与无孔结构一阶模态振型

由图2可知，腹板开孔虽不会显著改变结构振型，但腹板开孔后，会更易激起开孔腹板处的振动以及与开孔腹板相邻甲板的振动，从而影响整个结构的声振特性.

在模态分析的基础上，为了得到结构在一定激励和边界条件下的动态响应，故对结构进行了谐响应分析.谐响应分析中采用位于甲板板中心位置的垂直于甲板板的集中力激励，载荷幅值为10 N,频率范围为0～100 Hz，步长为5 Hz，由工程经验可知，钢结构的结构阻尼损耗因子取值范围为0.02～0.05，本文结构阻尼损耗因子设为0.03，给予四边固支边界条件.并运用有限元耦合间接边界元方法进行了声辐射分析，结果见图3～4.

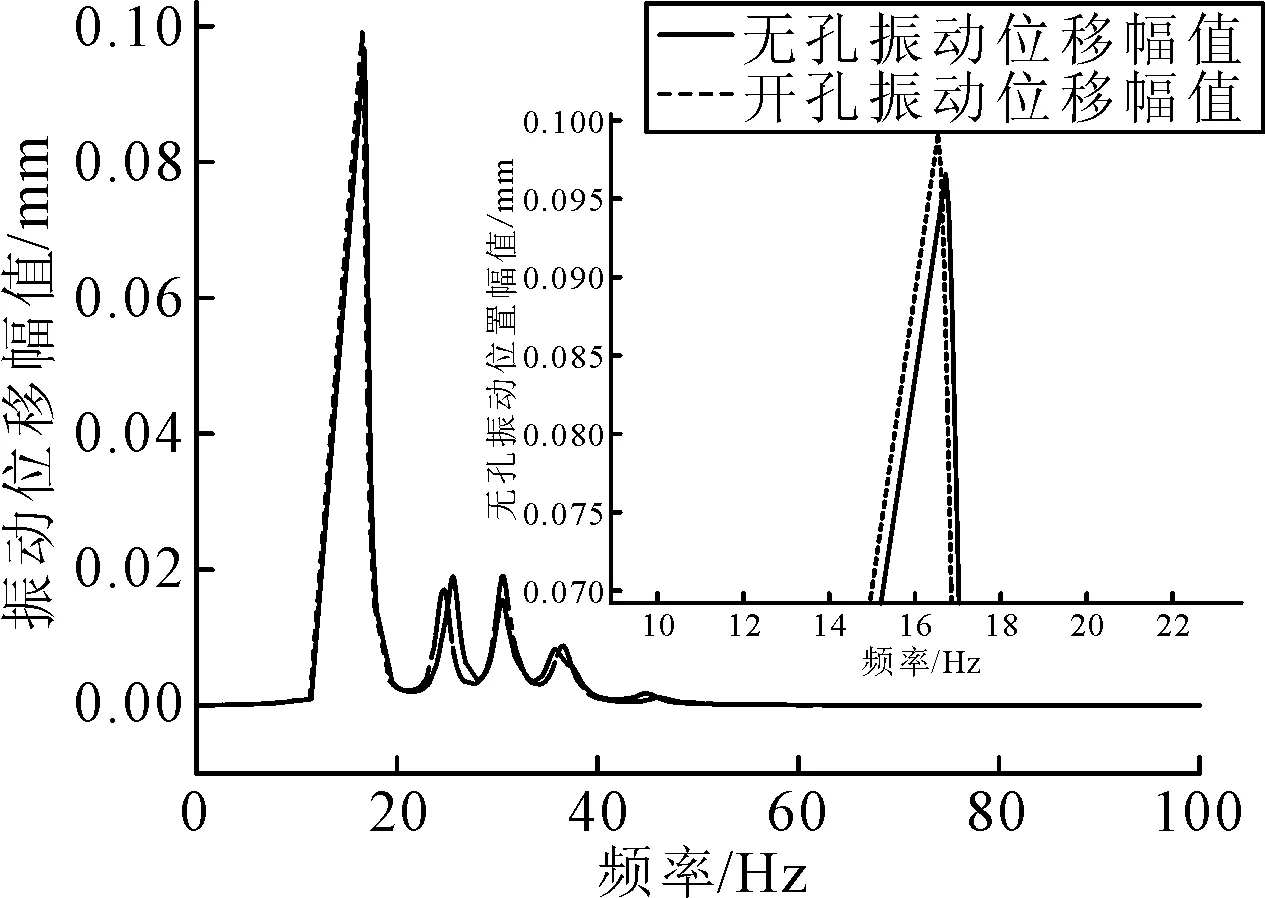
图3 开孔与无孔结构振动特性分析

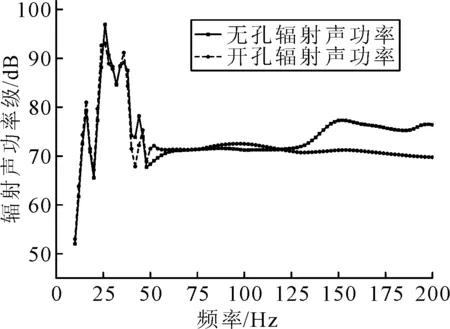
图4 开孔与无孔结构声辐射特性分析

由图3～4可知，大型邮轮所运用的大跨度开孔高腹板板架结构较普通加筋板结构而言，具有更大的振动位移幅值和更复杂的声辐射特性.因此，有必要对此类结构的声振特性进行研究，从而为其减振降噪提供参考.

2.2.2结构参数对结构振动特性影响分析

图5为不同腹板高度、厚度和面板宽度振动位移幅值曲线，由图5可知，激励力频率在结构一阶固有频率附近的时候，结构振动位移幅值存在极大值，说明此时结构更容易产生共振.随着腹板高度的增加,共振峰向右移动，结构振动位移幅值逐渐降低，腹板高度为500 mm时，位移幅值最小，具有最优的振动特性.随着板厚的增大，结构振动的位移幅值具有减小的趋势，同时由于改变了板厚，影响了结构的质量和刚度分布，使得结构的固有频率发生改变，结构振动的峰值点往高频移动.

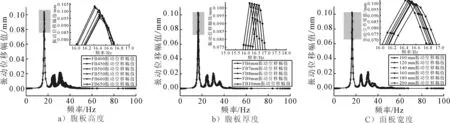
图5 不同腹板高度、厚度和面板宽度振动位移幅值曲线

图6为不同尺寸圆孔、腰圆孔和组合孔振动响应曲线，由图6可知：当开孔率达到62.2%时，虽然结构重量最轻，但是其振动位移幅值最大，说明此种开孔率的孔型具有最差的振动特性，更容易向外辐射噪声.随着开孔率的增大，振动位移幅值的峰值逐渐向高频段移动，并且开孔率为57.7%时，具有最大的共振频率及最小的振动位移，说明此种孔型具有最优的振动特性.当开孔率相同时，组合孔具有较小振动位移幅值，并有较大的共振频率，因此在保持开孔率的前提下，应优先选择组合孔以保证结构具有最优的振动特性.

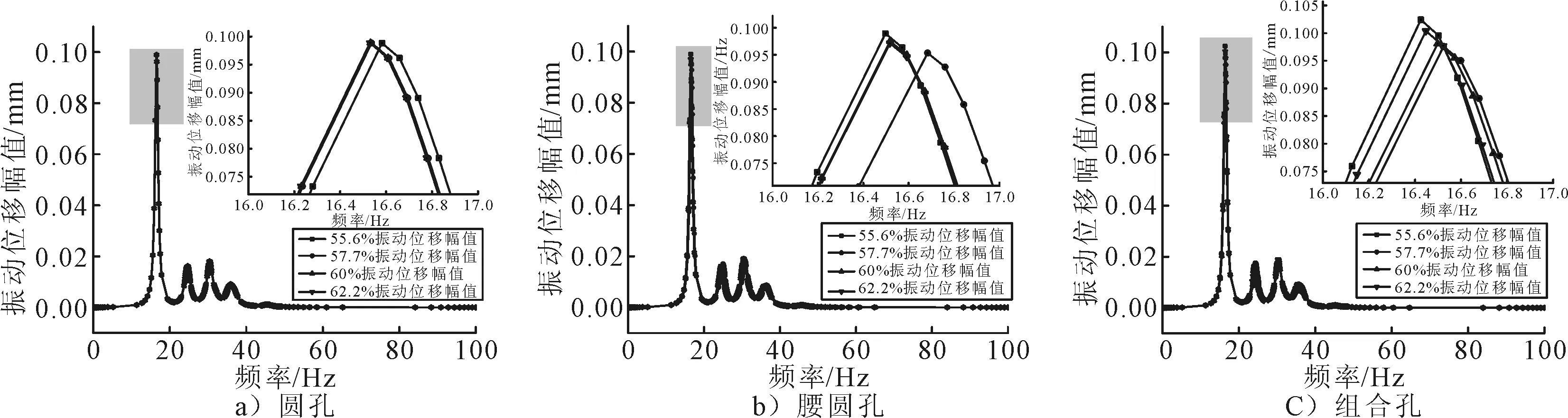
图6 不同尺寸圆孔、腰圆孔和组合孔振动响应曲线

2.2.3结构参数对结构声辐射特性影响分析

将振动响应结果作为声学计算的边界条件，利用边界元方法计算结构声场分布，计算频率范围为10～500 Hz,步长为2 Hz，以甲板板中心为球心，构造半径为10 m的场点，分析得到指定场点的辐射声功率级.

图7为相同尺寸不同孔型振动响应曲线.由图7可知：随着腹板厚度的增加，结构的固有频率随之增大，辐射声功率级也呈下降趋势，但是增加腹板厚度势必会影响结构轻量化设计.

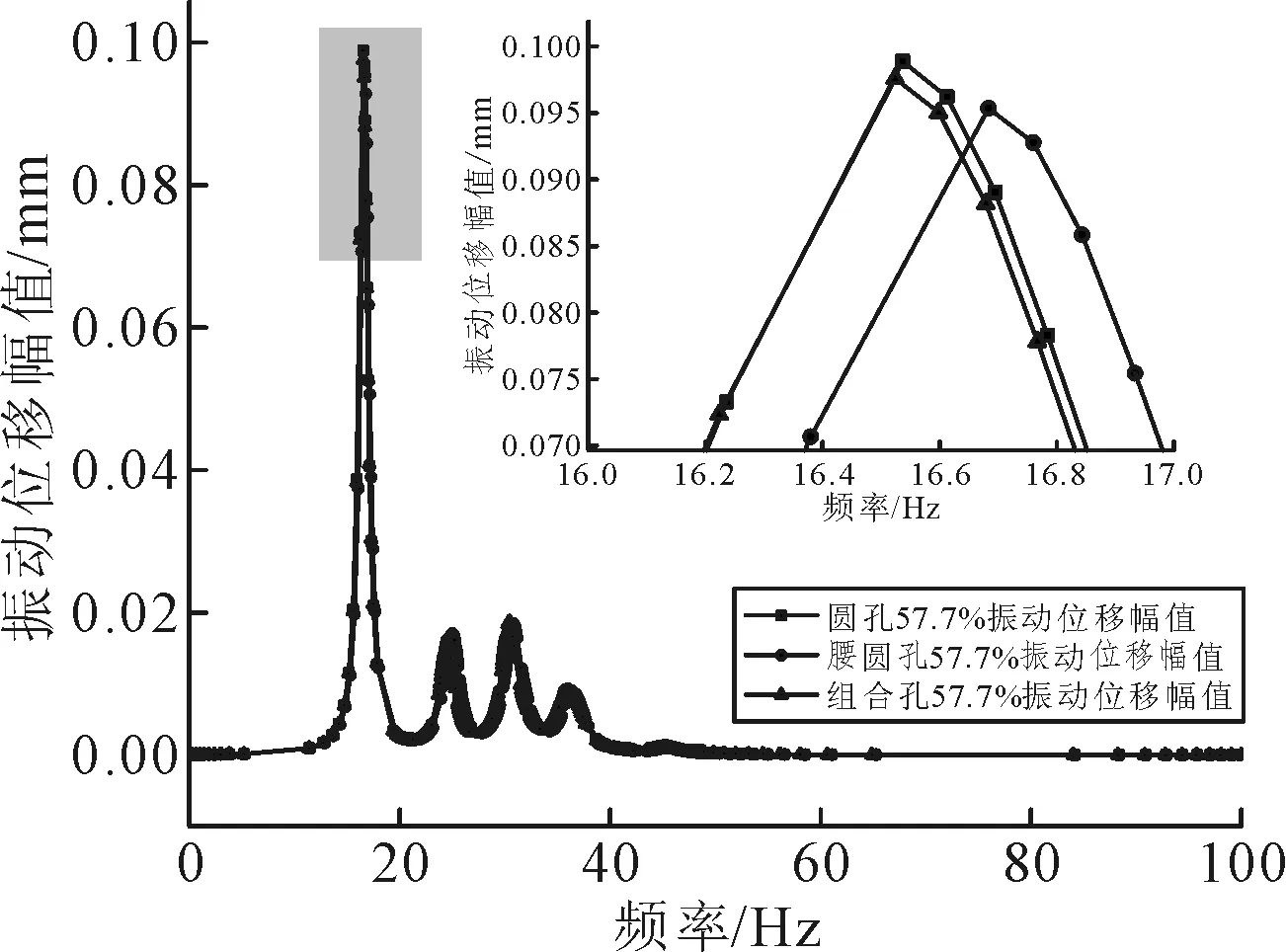
图7 相同尺寸不同孔型振动响应曲线

图8为不同腹板厚度、高度和面板宽度对结构声辐射特性影响曲线.由图8可知：随着腹板高度的增加，结构的辐射声功率级呈现先减小后增大的变化过程，当腹板高度为450 mm时，结构的辐射声功率级最小，腹板高度650 mm时辐射声功率级最大.因此，在需要增高腹板高度来满足结构功能需求时，腹板高度越高，越应注意其振动与声辐射的控制.

由于结构面板对结构刚度矩阵参与较小，面板厚度的变化对结构辐射声功率级影响也相对较小.因此，在满足结构强度要求的基础上，可以适当减小面板厚度来降低结构质量.

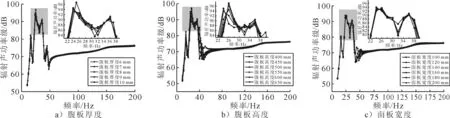
图8 不同腹板厚度、高度和面板宽度对结构声辐射特性影响曲线

图9为不同尺寸腰圆孔、组合孔和相同开孔率不同开孔形式对结构声辐射影响曲线.由图9可知，对于不同开孔率的腹板开椭(腰)圆孔结构而言，当腹板高度一定时，开孔率为57.7%的开孔类型具有最小的辐射声功率级，并且辐射声功率峰值向高频移动.对于不同开孔率的组合孔结构而言，随着开孔率的增大，结构辐射声功率级逐渐增大.与椭腰圆孔类型一样，开孔率为57.5%的组合孔具有最小的辐射声功率级，说明此类开孔率对于特定腹板高度而言，具有最优的声振特性.对于相同开孔率不同开孔形式结构而言，组合孔具有更小的辐射声功率级，但是椭腰圆孔结构具有更轻的质量.因此，在选择开孔形式的时候，应该兼顾舱室振动噪声标准以及轻量化要求.

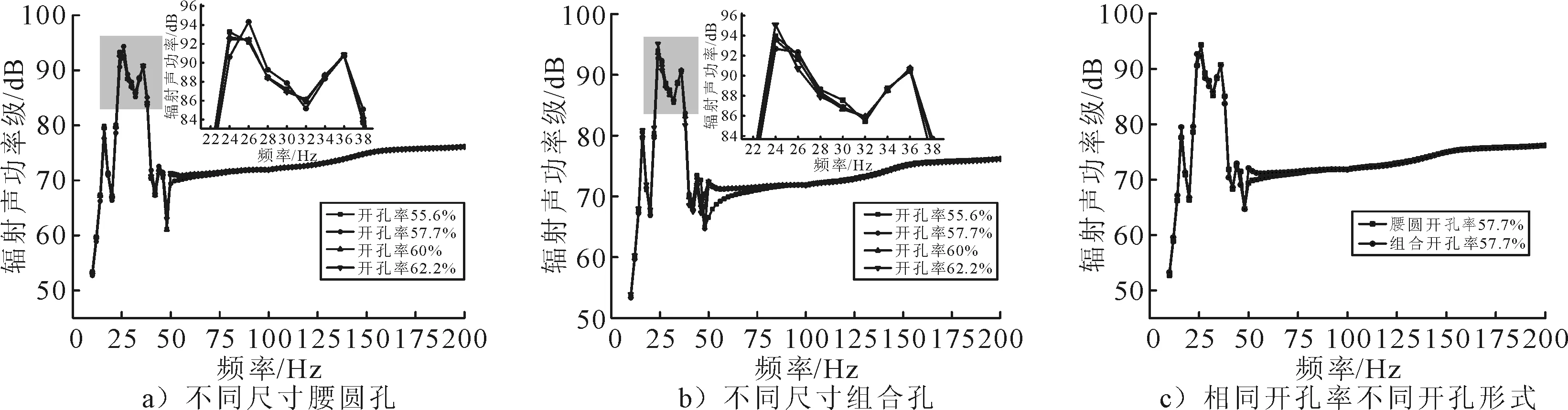
图9 不同尺寸腰圆孔、组合孔和相同开孔率不同开孔形式对结构声辐射影响曲线

2.3 边界条件对结构振动特性影响分析

考虑几种典型的边界条件，从甲板板左边长边开始，按顺时针方向四边固支(CCCC)，三边固支一边自由(FCCC或CFCC)，两边固支两边自由(CFCF或FCFC).运用有限元方法计算结构在不同边界条件下的模态振型以及振动响应结果见图10.

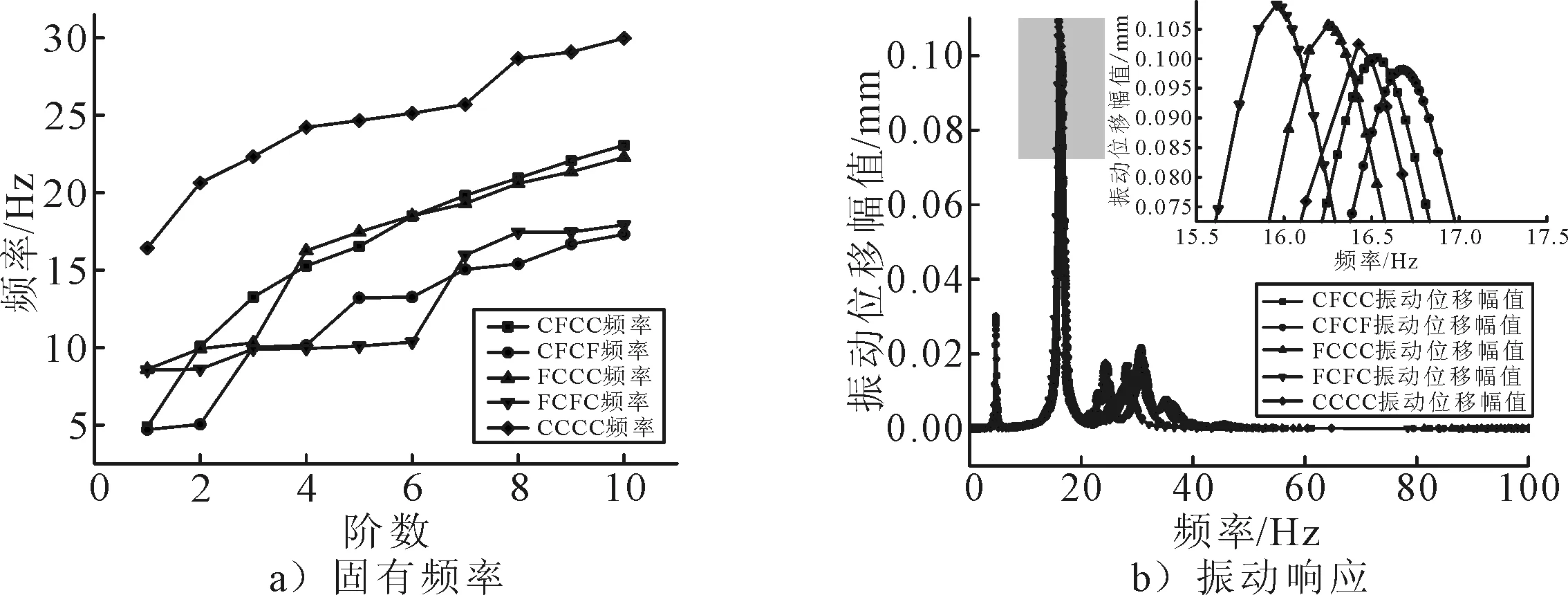
图10 不同边界条件下模态振型以及振动响应结果

基于上文探讨的边界条件，各类边界条件下的结构振动与声辐射计算结果见图11.

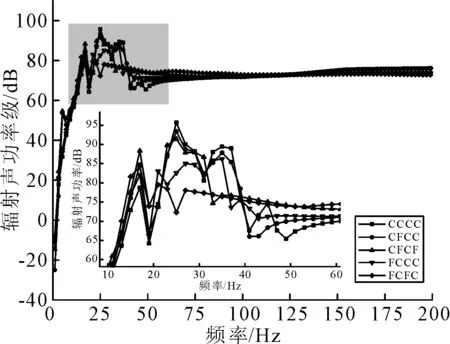
图11 不同边界条件对结构声辐射影响曲线

由图11可知：结构的声辐射特性与其边界条件有很大关系.随着结构固支边数量增加，结构四边的约束相应增强，结构刚度增大使得结构的固有频率相应增大，结构的辐射声功率级以及辐射效率相应降低，自由约束边数越多，结构越易产生振动并向外辐射噪声.当激励频率高于结构固有频率后，边界条件的变化对其声振特性影响较小.

2.4 激励位置对结构声振特性影响分析

分别在甲板板选取强构件处以及非强构件处激励各两处，腹板开孔区域激励两处进行振动响应分析，采取四边固支的边界条件，外部激励力的大小为10 N,频率范围为0～100 Hz，间隔5 Hz，具体激励位置见图12.

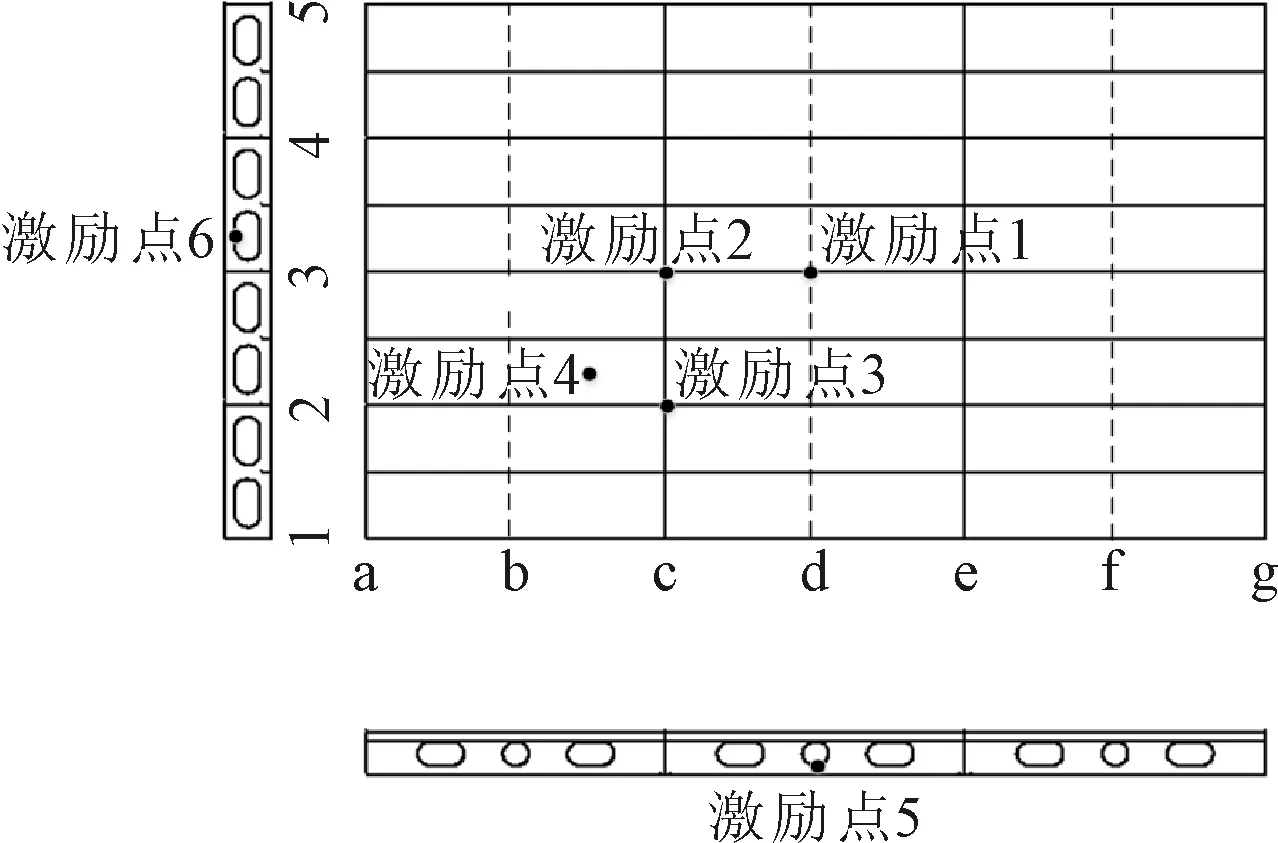
图12 不同位置激励布置图

图13为面板、腹板不同位置激励点振动位移曲线.由图13可知，不同的激励位置在相同的响应点的位移幅值具有较大差异，其中纵骨处的激励所产生的振动位移幅值最大，当激励点位于结构强骨材上方时，结构的振动位移会出现很大程度的下降，这是因为强骨材区域结构强度较非强骨材区域强.对与腹板开孔处的激励来说，横梁腹板振动位移幅值大于纵桁腹板振动位移.

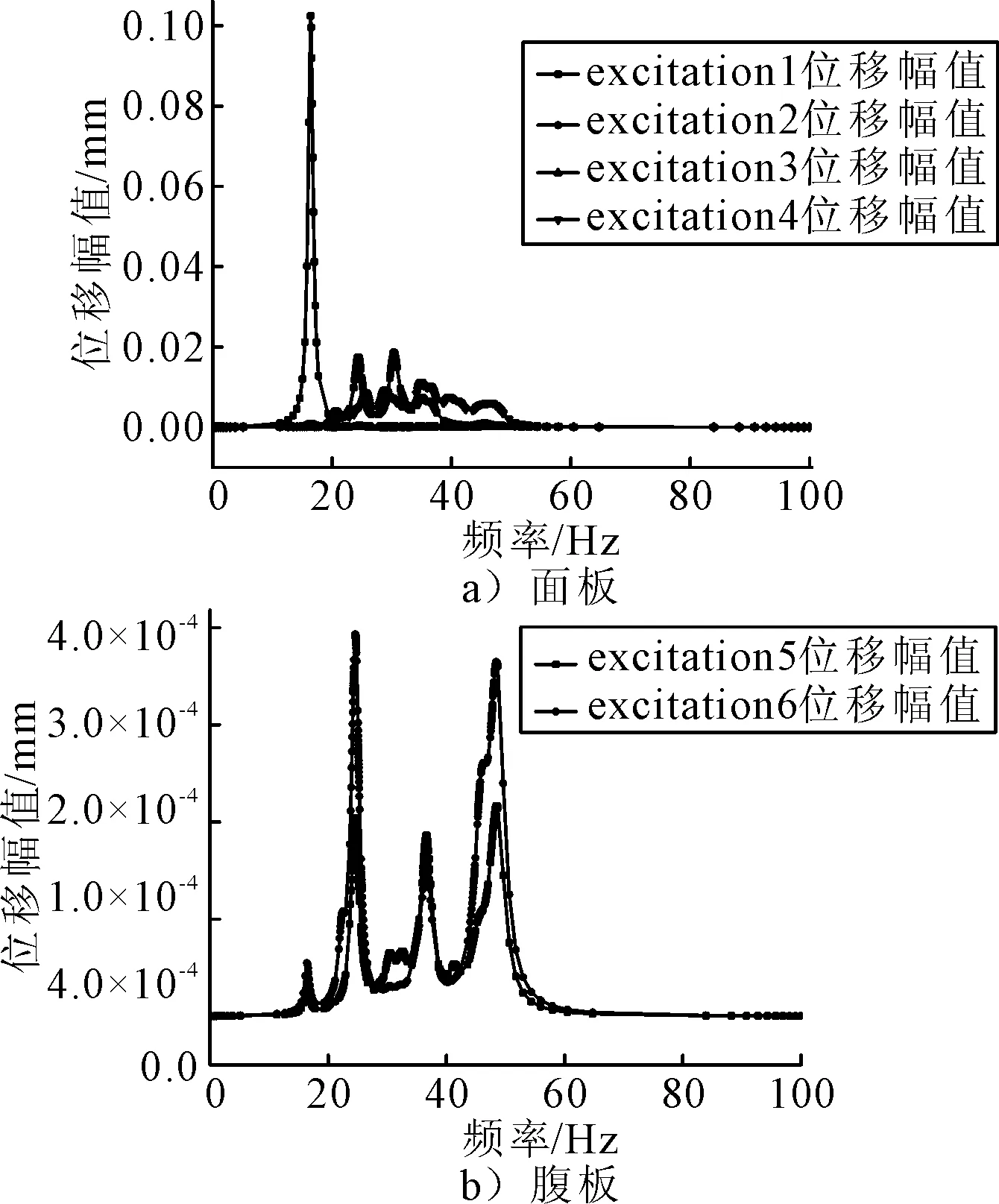
图13 面板、腹板不同位置激励点振动位移曲线

在结构振动分析的基础上，进行了不同激励位置下结构声辐射分析，计算结果见图14.

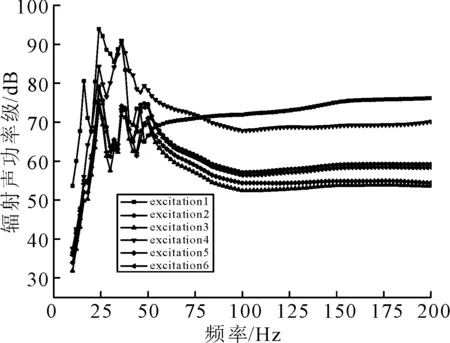
图14 不同激励位置对结构声辐射影响曲线

由图14可知，不同激励位置对结构声辐射特性影响很大.当激励位置处于甲板板弱构件区域时，结构的辐射声功率级大于其他激励位置，当激励位于结构强构件上方时，激励点3辐射声功率级均小于其余激励位置，这是因为激励点3位于横梁和纵桁交叉区域，此区域具有相对于其余区域更强的刚度，因此振动声辐射特性最优.当激励点位于腹板位置时，纵桁激励的辐射声功率级大于横梁位置，当纵桁开孔作为管道布施作用时，应采取更加严格的减振降噪措施.

3 结 论

1) 腹板高度、厚度，开孔率以及开孔形式均对板架结构的振动与声辐射特性产生较大影响，腹板高度为450 mm，开孔率为57.7%时结构具有相对较小的辐射声功率级.面板厚度和宽度对结构的声振特性影响较小.

2) 开孔参数对板架结构具有最优的固有特性.对于具有相同开孔率不同开孔类型而言，圆孔具有最大的固有频率，但是此种开孔类型结构质量最大，椭圆孔虽然能使结构重量减少最多，但是其固有频率最小，组合孔类型结合了另外两种开孔类型的优点，既保证了结构重量的减轻，也兼顾了其对结构固有特性的影响.

3) 增加结构边界约束有利于降低结构的振动与声辐射水平.

4) 当激励处于板架非强构件上方时，会产生较大的声辐射.当布施管道时，沿船体横梁腹板布施具有较小的振动与声辐射水平.