基于卡尔曼滤波的水下航行器水动力系数辨识方法
吕帮俊 黄 斌 明廷涛 彭利坤
(海军工程大学动力工程学院1) 武汉 430033) (上海地区装备修理监修室2) 上海 200136)
0 引 言
在潜艇或水下航行器设计过程中,必须对其操纵和控制性能进行系统的仿真和测试,这些都依赖于精确数学模型的建立.而水下航行器数学模型中大量的水动力和力矩项,将显著影响其性能预报结果,因此必须对描述其水动力和力矩的系数进行准确估计[1].在设计阶段,模型试验和计算流体动力学(computational fluid dynamics,CFD)是获取水动力系数的主要手段,对于实际的水下航行器来说,实尺度试验结果无疑是最为可靠与可信的,但由于其相对较高的成本而不受青睐.水下航行器运动模型中的水动力系数主要可分为两类,其中的惯性类水动力系数,也即附加质量通常可以采用细长体理论进行估算,且能获得足够的精度,因此,影响模型预报精度的核心是粘性类水动力系数,尤其是其中的一阶项也即水动力导数对模型计算结果的影响尤为突出[1],大量的研究工作致力于解决这一具有挑战性的问题.其中,系统识别(system identification,SI)理论,以相对较小的代价即可在线或离线辨识出高精度的水动力系数,成为水下航行器设计阶段获取水动力系数的一种强大且实用的方法[2-4].将基于SI理论的辨识方法与水动力系数测试或自航模试验相结合,已成为利用试验数据建立系统精确数学模型的有力手段[5].
Kalman[6]基于两步贝叶斯过程,即预测更新与测量更新,提出了卡尔曼滤波器(Kalman filter,KF),成为线性系统最优化自回归数据处理算法.然而,大多数水下航行器的运动方程均存在一定程度的非线性,无法直接应用传统KF.扩展卡尔曼滤波(extended Kalman filter,EKF)的提出使得卡尔曼滤波理论的应用拓展到非线性领域,EKF的基本思想是利用泰勒展开将非线性系统线性化,使得原有理论继续适用于非线性系统,而此时的EKF成为一种次优滤波.Abkowitz[7]将其应用于船舶试验试航中,提供了一种“测量”船舶水动力系数的方法,并验证模型方程的准确性.EKF的计算精度依赖于线性近似的有效性,如果线性化处理不当或是系统具有强非线性将会引起算法发散[8].Julier 等[9]结合无迹变换与卡尔曼滤波提出了无迹卡尔曼滤波(unscented Kalman filter,UKF)方法,避免了 EKF 线性简化及求解雅克比矩阵等问题,被广泛运用于非线性系统识别.Sabet等[10]采用UKF来估计AUV空间运动模型中的未知增广状态量(包含10个耦合水动力系数),并与EKF进行比较,表明UKF无论是在估算精度还是收敛速度方面均优于EKF.Chowdhary等[11]研究了扩展UKF、简化UKF以及EKF等三种算法对于飞行系统参数识别的有效性,通过对比发现,三种算法在估算能力上相差无几,UKF在收敛时间和估计可靠性方面具有一定的优势,但要花费更多的计算代价,而EKF算法始终可以返回高质量的计算结果,并且在计算需求方面要求最低.褚式新等[12]采用UKF算法对USV二阶非线性操纵响应模型参数进行了辨识,得到与真实值较为接近的结果,进而对USV的操纵性进行了有效预报.VAN等[13]对UKF算法进行优化提出了SRUKF,采用QR和Cholesky分解等两种高效的矩阵运算,将UKF算法进行N维未知参数向量估计时的计算复杂度由O(N3)降低到O(N2).Belanger等[14]采用SRUKF算法对潜艇标准运动方程中的全部120多个水动力系数进行了辨识,计算结果的平均误差仅约0.2%,具有很高的辨识精度.因此,目前已开展研究集中在水下航行器空间运动方程水动力系数的识别,由于模型具有强非线性,一般都认为UKF或SRUKF算法比其他算法更具优势.本文针对水下航行器垂直面机动非线性数学模型中的水动力导数辨识问题,建立了参数辨识模型,分别采用EKF和SRUKF算法对垂直面运动影响最为显著的6个参数进行了辨识,并对辨识结果进行了分析比较.
1 水下航行器垂直面运动数学模型
采用国际拖曳水池会议(ITTC)推荐以及造船与轮机工程学会(SNAME)术语公报的体系[15],描述水下航行器空间运动的坐标系和主要参数见图1.
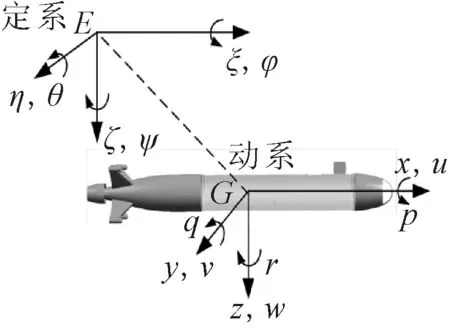
图1 描述水下航行器运动的坐标系和主要参数
对Gertler发表的潜艇标准运动方程进行简化,只考虑垂直面的升沉速度w,纵倾角速度q,纵倾角θ,深度ζ,输入控制量首舵角δb和尾舵角δs,同时假设水下航行器在垂直面内作弱机动,保持较低的航速u=u0不变,w、q、θ、δb、δs为小量,得到垂直面三自由度运动方程.
(1)
(2)
(3)
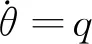
(4)
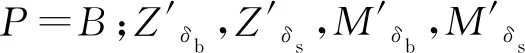

表1 模型艇参数值

表2 无因次水动力系数及测定值
2 水动力系数辨识模型
对于一个实际的非线性系统,通常采用连续-离散混合滤波方法,即采用连续的状态估算模型与离散的测量采样模型
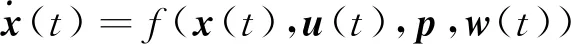
(5)
y(k)=h(x(k),v(k))
(6)
式中:x∈Rn为状态向量;u为输入向量;y∈Rm为观测向量;p∈Rl为未知参数向量;f(·)为系统动力学模型方程;y(·)为测量方程;k为离散的时间序列;w(t)≈N(0,Q)为过程噪声向量,v(k)≈N(0,R)为第k步的测量噪声向量,同时假定w(t)和v(k)都为均值为零的白噪声且彼此不相关.
参考式(5)~(6)给出的状态估算和测量采样模型,将式(1)~(4)所描述的水下航行器垂直面三自由度运动方程改写成矩阵形式

(7)
y=[θ,w,q]T
(8)
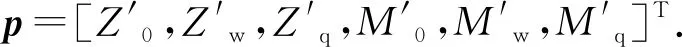
E=T-1S2,F=T-1S3
式(7)给出的运动模型是连续的,要通过计算机实现未知参数的在线估计,或是根据试验数据进行未知参数的迭代估计时,必须对模型进行离散化处理
(9)
式(9)中数值积分可以采用四阶龙格库塔积分算法
式中:b1=f(xk,uk,p)Δt;b2=F(xk+0.5b1,uk,p)Δt;b3=F(xk+0.5b2,uk,p)Δt;b4=F(xk+b3,uk,p)Δt;积分步长Δt=t(k+1)-t(k).
2.1 扩展卡尔曼滤波(EKF)参数辨识模型
当系统存在随机扰动和传感器噪声的情况下,EKF可以最优地估计非线性系统中的状态变量.为了对未知参数进行估计,通常采用的方法是将状态参数向量进行扩展,即把待识别参数作为额外的状态变量来进行估计
(11)
(12)
式中:扩展状态向量x*=[xT,pT]T∈Rn+l;0和I分别为零矩阵和单位阵;F(·)为采用扩展向量时的系统动力学模型方程.
通过EKF进行参数估计时分为两个步骤:第一步为预报,主要计算状态量以及状态误差协方差;第二步为测量更新,计算出所构造的扩展卡尔曼滤波器的增益,进行状态误差协方差矩阵的更新,以及对所预报的状态值进行更新.
1) 状态预测
(13)
(14)
2) 测量更新
(17)
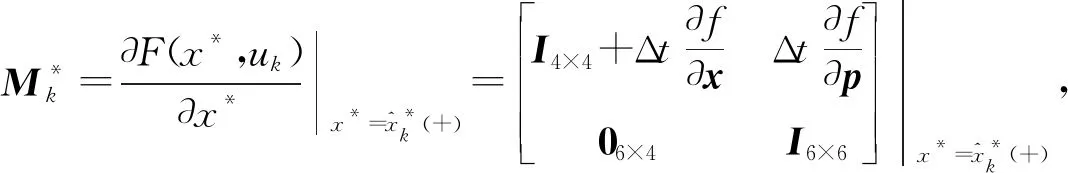
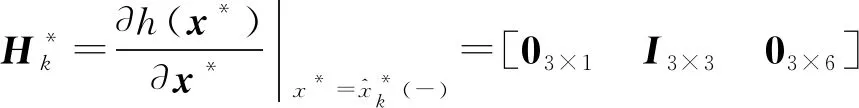
2.2 平方根无迹卡尔曼滤波(SRUKF)参数辨识模型
采用SRUKF进行参数估计时,状态预测与测量更新等基本步骤与EKF类似,但具体实施细节有一定差异.与EKF相比,SRUKF不需要对非线性系统方程进行任何线性化处理,而是利用概率分布构造Sigma点采样的方式,保持了原系统的非线性特征.此外,相对于UKF算法,SRUKF采用了高效的QR分解和Cholesky分解矩阵运算,极大的降低了计算复杂度.
1) Sigma点采样和状态预测
(18)
(19)
Dk|k-1=f(xk,uk,Pk|k-1)
(21)
(22)
2) 测量更新
(23)
(24)
(25)
(26)
(27)
U=κkSdk
(28)
(29)
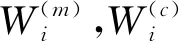
3 仿真算例分析
为了比较EKF和SRUKF两种算法进行水下航行器水动力系数辨识时的性能差异,采用模型艇作为仿真算例,相关参数见表1.进行参数辨识时所需的测量数据由水下航行器垂直面运动模型仿真产生,式(1)~(4)中的水动力系数取表2所列模型艇的无因次水动力系数测定值.
为了准确、迅速的进行水动力参数辨识,需要使水下航行器以一定的形式进行机动,尽可能激发垂直面的全部水动力分量,通常采用z型机动或深度、纵倾周期变化的振荡模式.本文仿真时取无人航行器航速u0=1.1 m/s,采用周期性操舵来实现上述运动,首、尾升降舵按照正弦规律操舵δb=δsin(0.03t),δs=δsin(0.04t),分别取舵角幅值δ=5°和10°,仿真时长t=3 000 s,步长Δt=0.1 s,水下航行器在垂直面的运动轨迹见图2,为了便于比较,两种算法采用同一组测量数据作为水动力系数辨识算法的输入.

图2 分别采用5°/10°幅值正弦规律操舵时无人水下航行器状态参数变化情况
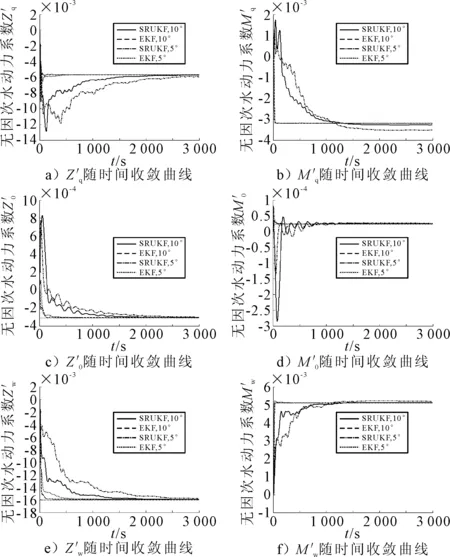
图3 无因次水动力系数随时间收敛情况
此外,从算法的平均收敛时间比较来看,文献[15]应用SRUKF算法辨识潜艇标准运动方程水动力系数所需时间约2 500 s,由图3可知:当操舵幅值分别为5°/10°时,采用SRUKF算法,全部水动力系数收敛到固定值所需时间约2 500 s/3 000 s,而EKF算法仅需要约100 s/600 s即可收敛到固定值.因此,EKF算法相较于SRUKF具有更快的辨识速度,且两种算法都受到操舵幅值的影响,也即水下航行器机动强度越大,水动力系数收敛速度越快
从理论上讲,SRUKF算法采用无迹变换,采样点没有经过线性化,也没有忽略高阶项,在求解非线性系统时具有更高的精度.但由仿真结果来看,对于本算例所涉及的水下航行器垂直面水动力导数辨识,无论是辨识误差还是收敛速度,EKF都优于SRUKF.分析其主要原因,是水下航行器采用低航速在垂直面正常机动时,采用非线性方程和线性方程的求解结果误差在5%之内,可以认为其垂直面运动模型具有较好的线性度,因此采用EKF算法对于其水动力系数辨识具有很好的效果.尽管采用SRUKF与EKF算法用于参数估计时,算法复杂度都为O(N2),但是EKF算法的收敛速度要明显优于SRUKF算法.
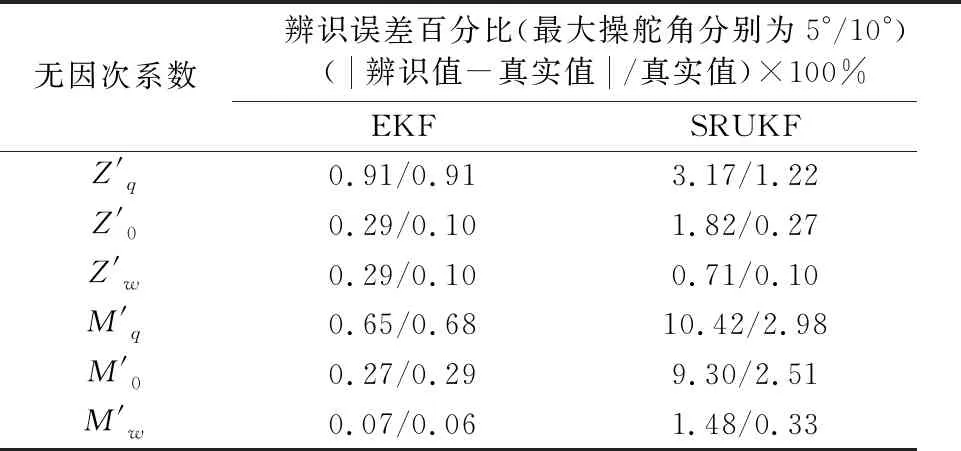
表3 无因次水动力系数辨识误差
4 结 束 语
文中分别采用基于卡尔曼滤波原理的EKF和SRUKF算法,以模型艇在垂直面正弦操舵机动时的纵倾角、垂速和纵倾角速度变化作为测量输入,对水下航行器垂直面运动模型中的6个核心水动力导数进行了系统辨识,取得了理想的辨识效果.尽管SRUKF算法理论上具有更高的计算精度,但通过仿真研究发现,SRUKF算法的辨识精度受模型艇机动强度的影响较大,对于线性度较高的水下航行器垂直面正常机动模型,无论是辨识精度还是收敛速度,EKF算法都要优于SRUKF,更适用于线性水动力系数的在线识别.

