水文地质试验对地下水化学场的影响研究

曹 楠, 张志鹏,孙 东,周亚萍,熊雨霞

(1. 四川省地质矿产勘查开发局成都水文地质工程地质中心，成都 610081;2. 四川省华地环境科技有限责任公司，成都 610081;3. 四川省环境保护地下水污染防治工程技术中心，成都 610081)

前 言

近年来，随着“绿水青山，就是金山银山”的生态文明建设理念的提出，政府加大了对水土污染防治技术的研究。水文渗透系数作为研究地下水污染迁的重要参数，普遍使用抽水试验获取[1～5]。该试验是经典获取水文地质参数的方法，但有以下问题有待解决[6-7]，其一，试验周期较长、效率低[8]，遇到突发地下水污染事件时，不能快速、准确获取小范围的水文地质参数[9-10]；其二，在污染场地内开展抽试验，会扰动加速污染羽的迁移扩散[11]；其三，试验可能改变局部地下水流场，人为扩大污染羽范围[12]；其四，抽水试验排出的水是否会引起二次污染的问题研究较少。

为了解决抽水试验的问题，研究了微水试验是否具备耗时短、效率高、影响半径小的特点[13]，是否是一种可以最大程度的减少对含水层扰动的替代办法[14-15]。

从资料收集入手，查阅获取水文地质参数的技术方法[16-17]，利用室内模拟地下水含水层装置，建立地下水模拟井，并在井中布设自动化水质和水位监测探头，监测抽水试验和微水试验过程中的地下水流场、化学场动态变化，评价两种试验类型对地下水流场、化学场的改变情况及获取渗透系数的准确性，探索替代传统水文地质试验获取水文地质参数的可能性。

1 材料与方法

1.1 材料与设备

主要仪器设备：电导率仪(DDB-303A)15只，定制3m长电导率电极15只；水位计(In-Situ Rugged TROll 100)2只，水位计(In-Situ Rugged TROll 200)1只；特制重锤1个；三维模拟试验装置尺寸为3.0m×1.0m×1.2m。

1.2 实验材料

主要材料：氯化物，化学纯；石英砂20～40目、石英砂10～20目、石英砂40～60目，粘土及泥沙等材料。

1.3 试验方案

三维模拟试验装置内共放置14根长度为1.3m的PVC管，井管直径为5cm，PVC管从下往上均匀布设2mm细眼至1m处，在PVC外围用纱布井钻眼处包裹起来，防止砂砾进入。

装置内由底部到顶部的填料依次为黏土层(0～10cm)、石英砂(10～90cm)、黏土层(90～100cm)，其中石英砂选择10～20目、20～40目混合均匀填放至槽内，每次填放10cm高度，两端放水淹没填埋介质，待介质均匀沉淀后再继续填放，反复操作直至填放高度为1m。填放时注意石英砂与隔板接触面用纱布包裹，以免石英砂或粘土堵住过水孔，模拟实验装置详见图1。

图1 模拟装置示意图Fig.1 Schematic diagram of analog device

1.3.1 系统概况

从三维模拟装置进水口通水，调节两侧水箱高度，左侧水位高度为1m，右侧水位高度为0.9m，让水流过整个装置12h，形成稳定的含水层。

1.3.2 试验条件优化

抽水试验中将抽水速率定为0.2、0.4、0.6、0.8L/min，记录井内水位下降速率，选择抽水速率与回水速率基本一致的速率作为抽水速率。通过抽水试验，获取该系统的含水层渗透系数，实验重复3～5次，验证该条件下获取参数的重现性。

微水试验中将水位计放入待测井中，选择重锤投放高度为10cm、20cm、30cm、40cm，读取水位及数据，选取引起水位计读数变化最大的高度进行微水试验，获取该系统的含水层渗透参数，实验重复3～5次，验证该条件下获取参数的重现性。

1.3.3 背景时间确认

整个系统不进行抽水试验和微水试验时，污染物随水流到达各监测井的时间成为背景时间。用以对比抽水试验和微水试验时污染物到达实验井的时间。

将水位计放入抽水井中，电导率仪放入1#～13#中，每个井放置1根电导率仪记录电导率值。

通过蠕动泵向14#内投入饱和NaCl溶液，加入后开始计时，记录其余13处监测井中电导率上升时的时间作为各井的背景时间，重复完成2～3次。

1.3.4 对化学场影响程度试验

在2#、3#、4#、13#井进行抽水和微水试验，利用最优试验条件进行试验。记录微水试验和抽水试验实验井周边监测井中电导率升高的时间，并与背景时间对比。

1.3.5 渗透系数验证试验

在1#-14#井进行抽水和微水试验，每个监测井试验3～5次，取平均值获得各井渗透系数。

1.4 试验模型

1.4.1 单孔稳定流抽水试验

单孔稳定流抽水试验，当利用抽水孔的水位下降数据计算渗透系数时，Q～s(△h2)关系曲线呈直线时[18]，公式为：

(1)

式中：K-渗透系数(m/d)；

Q-出水量(m3/d)；

H-潜水含水层厚度(m)；

h-潜水含水层在抽水试验时的厚度；

R-影响半径(m)；

r-抽水孔过滤器的半径(m)。

1.4.2 多井抽水试验

单孔稳定流抽水试验，当利用观测孔中的水位下降数据计算渗透系数时，若观测孔中的值s(或△h2)在s(或△h2)-lgr关系曲线上能连成直线，公式为：

(2)

式中：s1、s2-在s～lgr关系曲线的直线段上任意两点的纵坐标值(m)；

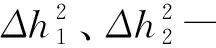
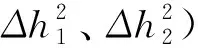
1.4.3 微水试验Hvorslev模型

Hvorslev在1951年通过大量试验后发现井内水位迅速变化后水位恢复的速度和时间成指数关系，水位恢复的时间与地层的渗透系数有关，恢复速率与井孔的结构有关。在此基础上，Hvorslev针对承压完整和非完整井的过阻尼微水试验提出一种半解析的方法[19-20]。Hvorslev模型井结构示意图详见图2。

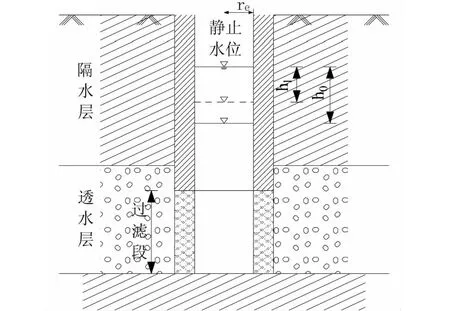
图2 Hvorslev模型井结构示意图Fig.2 Well structure diagram of hvorslev model

针对承压含水层中的地下水，Hvorslev发现当井孔中的地下水位瞬时改变后，流出或流进井孔的水流量与井孔附近含水层渗透系数之间的关系可表示为：

(3)

经过计算变形后，水平渗透系数公式：

(4)

其中形状因子F 根据过滤管与含水层的相对位置可分为3种情况，只要求得F 就可以求得渗透系数。结合本次试验，选择完整井，过滤管穿透整个饱和含水层。当过滤管的长度大于过滤管有效半径8倍时，即L/rwe>8，Hvorslev形状因子通过如下公式计算。

(5)

其中：R-微水试验的影响半径。

在计算第三种形状因子公式中，需要估算微水试验的影响半径R，查阅国外学者研究，取过滤管的长度或200rwe。

将式(5)带入式(4)后，得到Hvorslev模型公式为：

(6)

其中：R-微水试验的影响半径，为200rwe；

基本时间间隔TL，ln(ht/h0)≈-1，所对应的时间。

1.4.4 微水试验Bouwer-Rice模型

H.Bouwer和R.C.Rice建立的均质潜水含水层冲击试验模型是应用最广的潜水完整井冲击试验计算模型之一[21-22]。该模型假设含水层介质是不可压缩的、均质各向同性的，试验过程中，含水层的厚度近似保持不变。潜水井模型建立的示意图见图3。

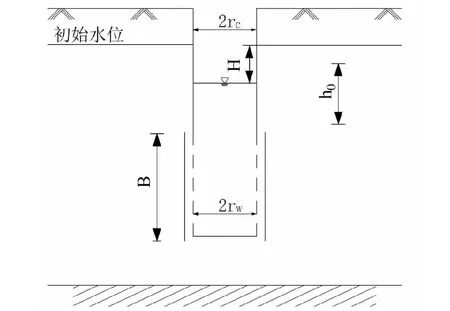
图3 Bouwer&Rice模型潜水井示意图Fig.3 Well structure diagram of Bouwer & Rice model

由于本次实验是瞬时向测井投放重锤引起水位变化，相对于整个测井中的水量来说很少，对测井中的水头改变不明显，对测井周围的含水层也不会产生明显的影响，不会产生越流补给的现象，因而可以假设地下含水层在冲击试验进行的整个过程中水位保持不变，该潜水井模型的理论推导如下：

试验中注入井中的水流运动过程满足变形后的Thiem公式：

(7)

式中：h(t)为测井中水位的位置水头(m)；H(t)为测井中水位的标准水头(m)。

结合初始条件：t=0时，H(t)=H0；以及在t时刻，H=H(t)，可以得到K的表达式：

(8)

式中：rc为井套管有效半径m；

rw井中心到填砾的距离m；

B为测井中滤管的长度m；

Re为微水冲击实验的有效半径，取经验值200rw；

t为测试时间(s)；

H0和H(t)为初始时刻和t时刻的压力水头(m)。

2 实验结果

2.1 条件优化

2.1.1 抽水速率优化

抽水速率分别为0.2L/min、0.4L/min、0.6L/min、0.8L/min观测水位变化，见图4。从图中可见，随着流量增大，水位降深也在增加。鉴于试验器材，降深变化不明显影响观测数据的准确性，因此本次试验采用降深为10cm左右(大致为含水层厚度的1/6)的抽水速率进行试验模拟。

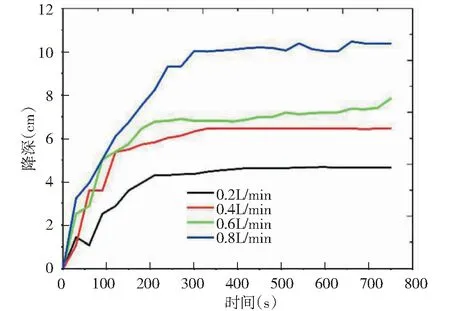
图4 抽水速率与降深关系图Fig.4 Pumping rate and drawdown

2.1.2 重锤高度优化

微水试验中选择不同投放高度10cm、20cm、30cm、40cm释放重锤，水位曲线变化见图5。从图中可以看到随着重锤的高度增加，水位变化幅度随之增大，但在实际观测中，当重锤投放高度超过40cm时，虽然水位变化最为明显，但落锤的一瞬间，受到水面与井管之间距离的影响，会有大量水飞溅溢出井口，后期在利用微水试验计算渗透系数时，重锤投放高度超过40cm时重复试验计算得到的渗透系数偏差最大，因此，选择投放高度为30cm。

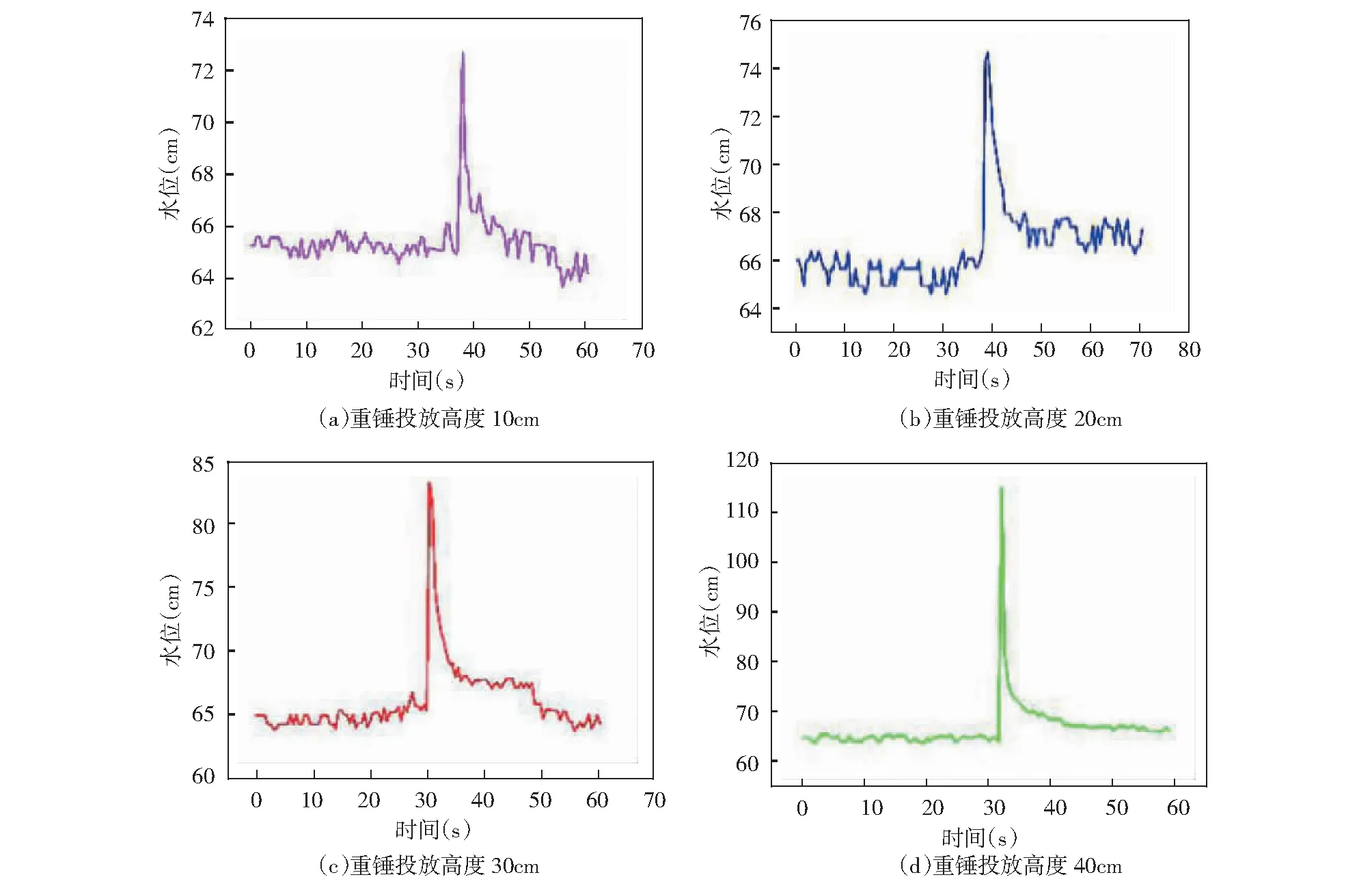
图5 重锤投放高度优化试验图Fig.5 Condition optimizationof slug test

2.2 对化学场影响程度试验

对整个系统进行试验，确定污染物到达各井时间作为背景时间，记录抽水试验和微水试验对污染物迁移时间的改变。

实验结果见表1，从实验结果来看，抽水试验会显著加快污染物的扩散，并改变地下水在区域上的流场。对2#、3#、4#、13#监测井进行抽水，均会缩短污染物到达2#的时间。对3#进行抽水试验时，对面的4#、7#、9#会出现不同程度污染物到达时间变长的情况。同时对4#进行抽水时，对面的3#、6#、8#也会出现污染物到达时间变长的情况。上述两组试验说明抽水试验不仅会加快污染物迁移的速率，还会改变局部地下水流场。

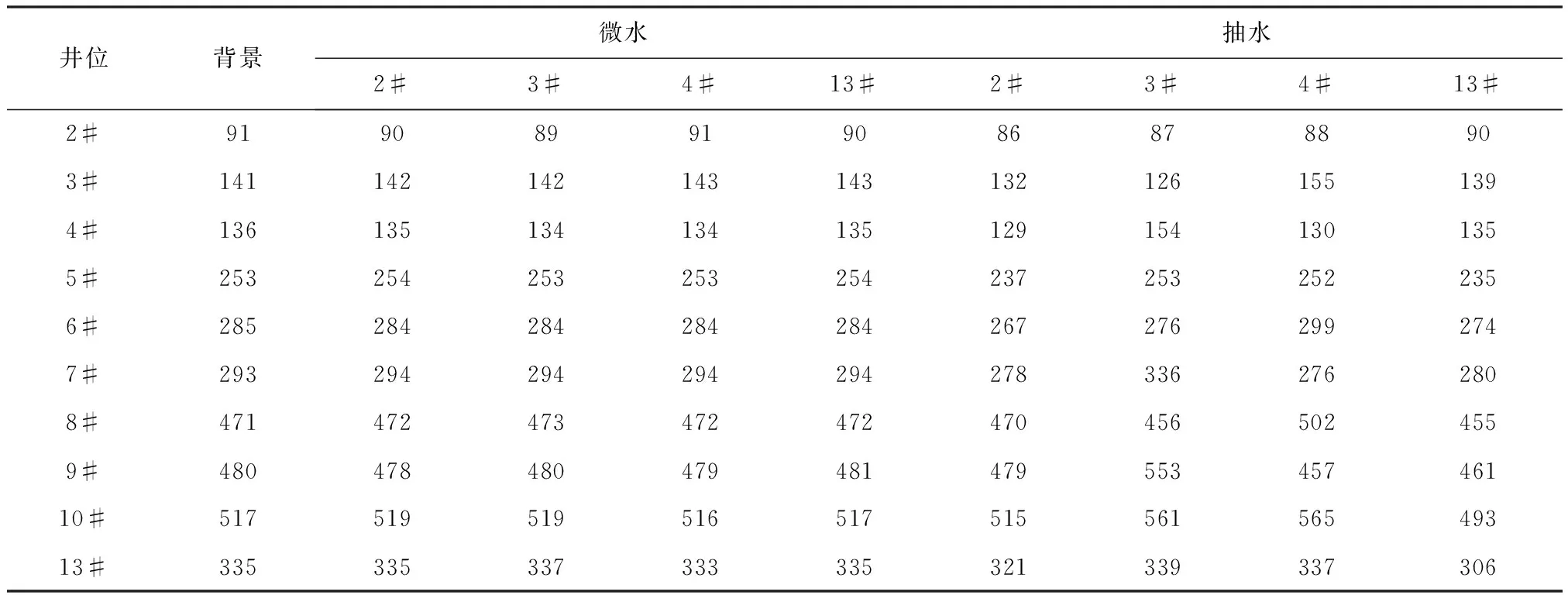
表1 井位电导率变化时间一览表Tab.1 The list of conductivity and time variation (min)

2.3 渗透系数验证试验

三维模拟试验完成了单孔抽水试验和有观测孔的抽水试验，每口监测井均完成了3次试验，取平均值。从表2中分析单孔抽水实验1#～14#渗透系数范围为6.4～13.3m/d，有观测孔的抽水试验1#～14#渗透系数范围为9.0～21.3m/d，微水试验Hvorslev模型1#～14#渗透系数范围为15.0～29.9m/d，微水试验Bouwer&Rice模型1#～14#渗透系数范围为10.5～22.4m/d，三维模式试验槽中渗透系数在6～30m/d这个范围内，试验结果看，槽内介质填充较均一，但也在局部存差异性。从图6中可知2#的渗透系数在不同模型计算下，渗透系数均明显高于其他监测井，这点是由于2#周边孔隙度大，存在局部强透水段。

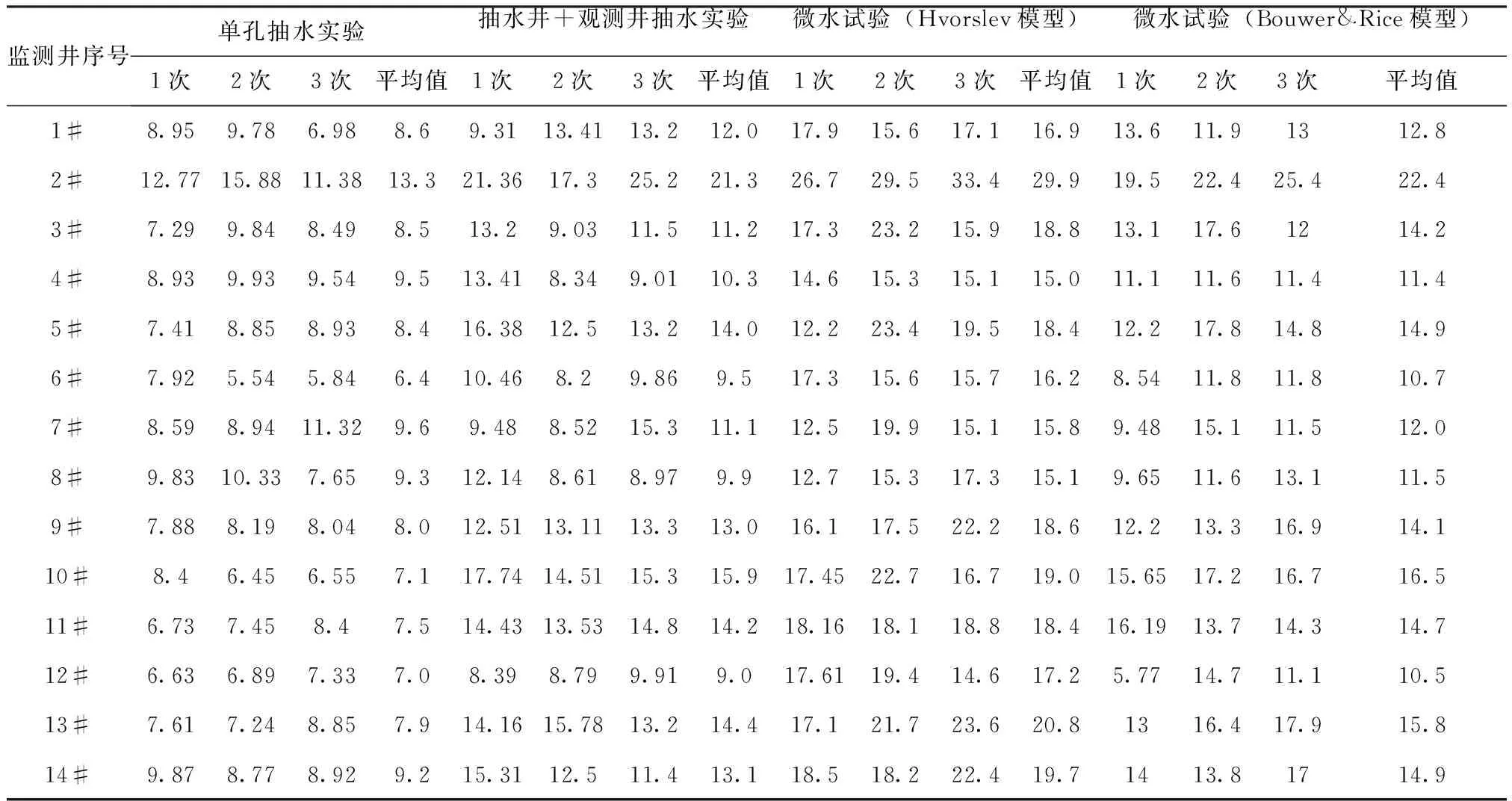
表2 水文地质试验渗透系数一览表Tab.2 The list of permeability coefficient by hydrogeological test (m/d)

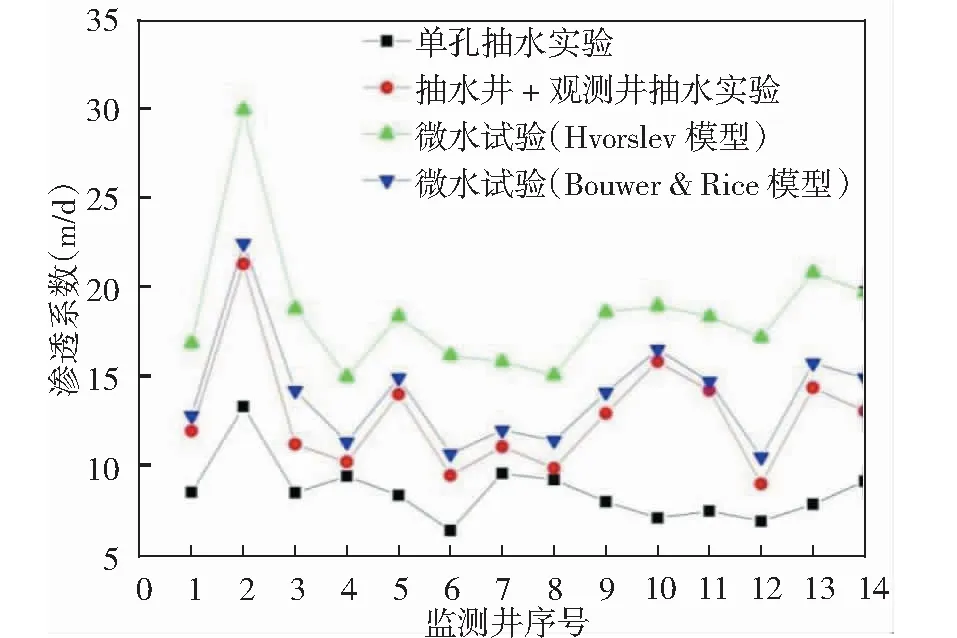
图6 监测井测定渗透系数关系图Fig.6 Permeability coefficient of monitoring well

抽水试验(观测孔)的渗透系数与微水试验中Bouwer&Rice模型获得的渗透系数基本一致。而单孔抽水试验与微水试验Hvorslev模型渗透系数相差较远。以抽水试验(观测孔)的渗透系数的对数为横坐标，其余模型的渗透系数值取对数拟合一元线性回归方程结果见图7和表3可知，Bouwer&Rice模型与抽水试验(观测孔)相关系数R2为0.951 0，从相关性来比较微水试验Bouwer&Rice模型>微水试验(Hvorslev模型)>抽水试验单孔。因此Bouwer&Rice模型更适合于潜水含水层渗透系数的获取。

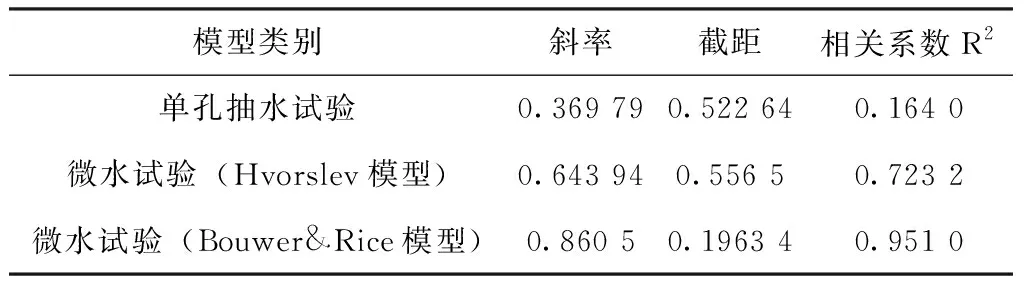
表3 线性关系一览表Tab.3 The list of linear relationship parameter

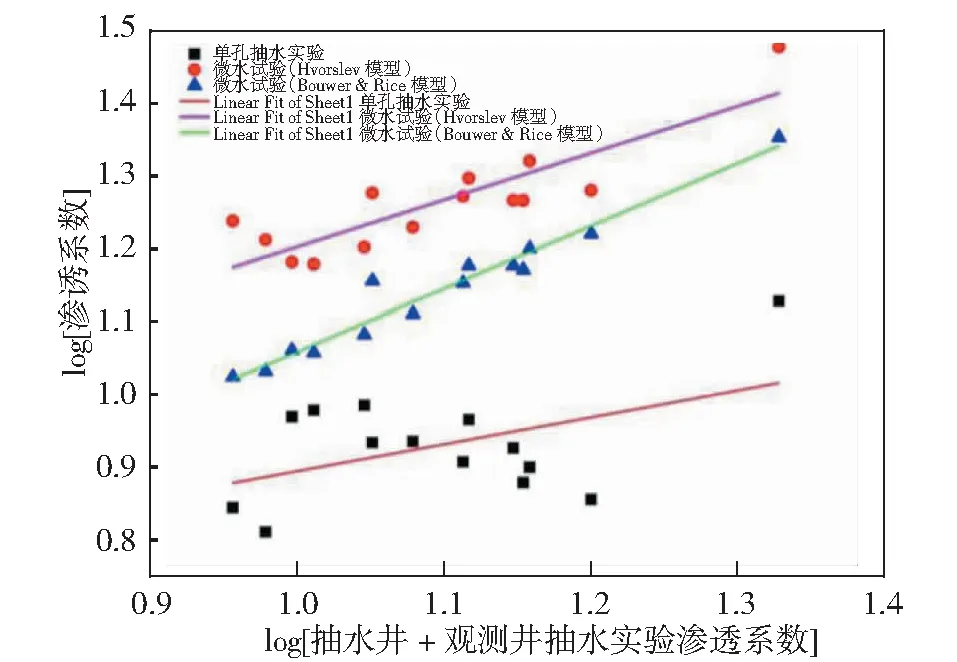
图7 不同模型渗透系数一元线性回归关系图Fig.7 Linear regression of permeability coefficient in different models

3 结 论

3.1 利用三维模拟装置，以饱和氯化钠溶液作为污染源观察监测井中电导率变化情况，通过与背景时间对比发现在相对高渗(中-粗砂)含水层中采用抽水实验会引起化学场及流场改变，加剧污染羽扩散，加快污染物的迁移；而采用微水试验对周边流场影响范围有限，对污染羽扩散的影响小。

3.2 本文创新性的采用水位计验证流场变化，用饱和氯化钠溶液作为污染源，以污染物到达各监测井的时间作为参考，证实了抽水试验加快污染物迁移速率，改变地下水流向的猜想。

3.3 对比抽水试验和微水试验获取的渗透系数，抽水试验获得的渗透系数与微水试验中采用Bouwer&Rice模型(潜水模型)获得的渗透系数进行线性拟合相关系数R2为0.951 0。表明微水试验在潜水相对高渗介质中(中-粗砂)亦可替代抽水试验获取渗透系数参数。

3.4 对比抽水试验和微水试验所需时间，三维模拟试验装置中抽水试验稳定需要480min，而微水试验时间在7～12min便可得到结果，表明微水试验在完成时间方面优势明显，具有推广应用价值。

3.5 通过研究证实微水试验相比传统抽水试验获取渗透系数所需时间更短、对含水层扰动更小、所需设备简单。在调查地下水污染场地，可优先选择微水试验，同时微水试验在反应含水层结构的非均一性方面更具有明显优势。