几种随机模型对北斗定位精度影响研究

孙 鹏

(新疆水利水电勘测设计研究院测绘工程院，新疆 昌吉 831100)

随着最后一颗北斗卫星成功发射，北斗三号全球导航系统正式开通运行。载波双频或者三频是北斗卫星提供的精准测量信号，在北斗二代提供频率为B1I、B3I的信号基础之上，北斗三代MEO卫星与IGSO 卫星将新增3个频点为B1C、B2a、B2b的信号，这五种频率信号为组合模型与双差模型提供数据基础。常见的组成双差方程中，定位解算时选择合适的随机模型至关重要，这关系定位解算中定权的优劣，一个合适的随机模型会大大提高双差方程中质量优的观测值权值，降低噪声或者误差较多的观测值的权。关于随机模型的选择，相关文献都做了大量的研究，其基本都是建立在GPS模型之上，考虑的因素也是GPS方面众多[1-2]，为此有必要将常用的随机模型应用于北斗三号卫星系统。

本文基于北斗开始大规模应用的基础上，以实测数据为例，以常见的四种随机模型为讨论对象，将四种随机模型分别应用在定位解算中，得出了各种随机模型在实际应用中的适用条件。这为双差方程或者单点定位中随机模型的选择提供参考与借鉴，也为北斗卫星全球组网、服务全球提供理论基础。

1 北斗卫星观测数学模型方程

北斗卫星提供的B1I、B3I、B1C、B2a、B2b五种频率信号，在组成观测方程时，不管是双差模型还是组合模型都可应用这五种频率信号组成方程。在应用最小二乘法计算时不仅需要观测值组成的数学模型，还需要观测值的先验信息。这些先验信息与单位权误差构成权值的模型，用来反映观测值自身的误差噪声特性。本文在利用北斗数据时，采用双差模型，即北斗卫星提供的双频数据为例，卫星间与测站间作差，即得到以下双差方程式：

(1)

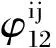
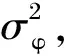
(2)

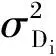
(3)

(4)

由此可见，双差观测值中的方差与协方差矩阵对定位解算结果至关重要，随后将分别介绍常见的四种随机模型在北斗卫星定位解算中的应用条件与适用条件。

1.1 等权随机模型

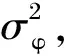
(5)

1.2 高度角随机模型

高度角随机模型是依据某一北斗卫星在某一历元时刻，该卫星相对于测站处的高度角计算建立的随机模型。该模型认为高度角与载波精度有很强的相关性，该理论依据的是高度角不同时，卫星发射信号传播途径也不相同。高度角与对流层延迟、电离层延迟呈正相关性，多路径误差减弱是由于高度角的增加导致的。所以常认为高度角与载波相位精度呈正相关性。载波相位的方差可以表示为高度角函数的形式[3]，如式(6)所示。

(6)

式中，f函数包括余弦函数、正弦函数、正切函数、指数函数等常见函数形式。

指数函数方程式[4]：

σ=σ0(1+ae-ε(t)/ε0)

(7)

式中，σ0为相位观测值的均方差，其满足卫星高度角90°时的数值；a为比例系数；ε(t)为时间与卫星高度角函数数值；ε0为基线两端点接收机公共观测卫星的高度角最大值。国外某学者利用大量的实验数据总结了式(7)中的参考值，如表1所示。

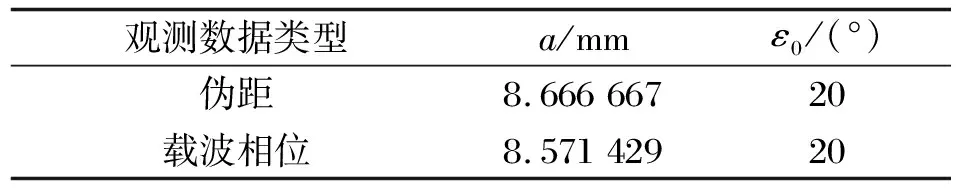
表1 指数函数方程式中系数的借鉴值

正弦函数方程式[5]：

(8)

式中，E为北斗卫星处于某一历元时刻的高度角。该高度角随机模型存在着不能准确反映低高度角卫星精度的缺点，在应用中常常采用改进后的正弦函数模型，该模型如式(9)所示。

σ2=a2+b2/(sin(E))2

(9)

式中，a、b常取经验值a=4 mm、b=3 mm。

正切函数模型[6]:

(10)

式中参数含义如前文。

1.3 载噪比随机模型

载噪比(C/N0)为载波在1 Hz宽带上的能量输出与噪声在1 Hz宽带上的输出比值。该比值与多种噪声有关，如信号传播途径中的电离层、大气延迟、接收机端的多路径误差、接收端的硬件，该数值根据多次试验取45 db-Hz。国外某组织根据该比值推导了如式(11)所示的SIGMA-ε函数模型[7]。

(11)

式中，Ci可用式(12)计算而得：

(12)

式中，Bi为相应频率载波的带宽，Hz；λi为该频率载波的波长，m。北斗三号星通常取CB1I=0.002 24 m2Hz，CB3I=0.000 77 m2Hz。若排除其余干扰因素，或者为一定值时，C/N0与高度角成一成不变的函数关系。当外界影响条件发生变化时，其C/N0值比相同高度角情况下的数值要小。Brunner研究员利用C/N0数值提出了SIGMA-Δ非确定性模型：

σ2=Ci×10-(C/N0measured-aΔ)/10

(13)

式中，Δ为实际获取值与条件值的差值；a为经验系数，一般取2。

1.4 信号强度随机模型

本节阐述的北斗卫星随机模型与前面叙述的随机模型相比较，更能准确反映出载波观测值的质量，但只有接收机能输出C/N0原始值时，才可以应用该模型。RINEX2.1版本以上的方可输出C/N0数值，但由于没有一个输出国际标准统一格式，所以导致很大一部分转换程序不能输出该数值。在标准格式RINEX2.0中，数据排列倒数第一位整数就是相应频率载波的信号强度，对应的C/N0值通过下式得到[8]：

(14)

由于北斗卫星在B1I、B3I、B1C、B2a、B2b这四种频率上的不同，直接导致其输出C/N0数值不同，频率低，输出C/N0值低。为使信号强度保持正负相关性一致，某些情况可在北斗信号接收机的相应低频率信号强度上加一常数4。信号强度本质上就是C/N0值的缩减值，于是信号强度的观测值方差公式为[9-10]：

(15)

2 实验与分析

2.1 实验一

本次实验位于某高校数据采集场地，基线两端接收机位于教学楼楼顶，视线无遮挡，视野开阔。该基线长90.8 m，一端为基站，另一端基线点为流动站，二者高差较小。数据接收采用2台iGMAS型号北斗接收机，该接收机可接收北斗卫星五种频率数据。数据采集时间为2020年6月20日，数据采样率为1 s，本次实验采用500个观测历元，卫星截止高度角为10°。在内业数据处理中，增加了C/N0观测值输出。利用成熟的研究型开源软件GAMIT软件包中Track模块进行解算，本次实验为比较四种随机模型对北斗卫星的适用条件，将四种随机模型利用FORTRAN语言加入到Track模块中，其中双频率数据选择B1C、B2a，定位结果如图1所示。定位结果采用内符合精度统计北(N)、东(E)、高程(U)精度指标，如表2所示。

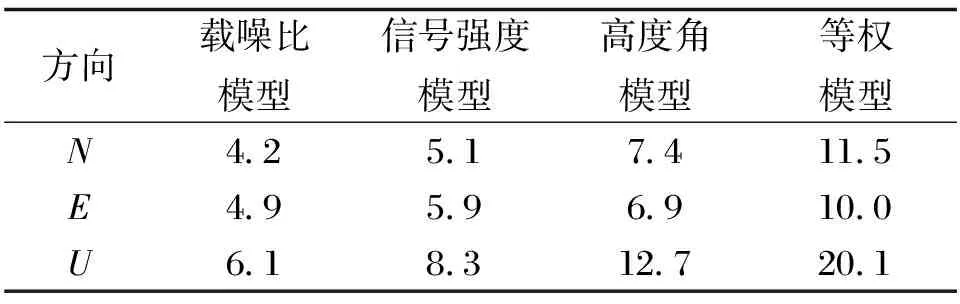
表2 四种随机模型的内符合精度值/mm

由图1可知，北方向、东方向中这四种随机模型均表现出平稳的定位结果，高程方向由于受到更多误差的影响定位结果较为波动。在四种随机模型定位结果中，载噪比定位结果最为平滑，信号强度、高度角定位结果次之，等权随机模型定位结果平滑效果最差。

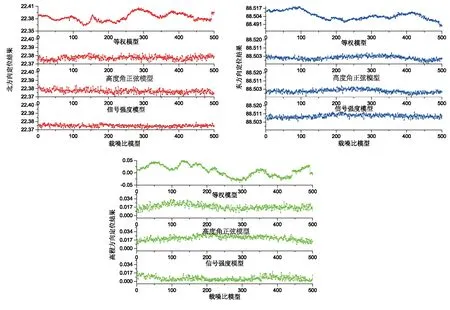
图1 流动站依据不同随机模型获取的坐标值

由表2可知，文中介绍的四种随机模型定位精度由低到高为等权随机模型、高度角随机模型、信号强度随机模型、载噪比随机模型，如北方向载噪比定位精度为4.2，等权模型定位精度11.5，东方向载噪比定位精度4.9，等权模型定位精度10.0。卫星处于低高度角时，大气延迟与多路径加剧了卫星观测值中噪声，所以采用高度角随机模型可有效减弱多路径与大气延迟的影响，如高度角随机模型北方向、东方向、高程方向定位结果分别为7.4、6.9、12.7，均优于等权模型定位结果11.5、10.0、20.1。载噪比模型、信号强度模型定位结果优于高度角模型，可证明载噪比随机模型与信号强度随机模型比高度角模型更能反映观测值质量。

当卫星信号出现失锁或者遮挡情况时，即使卫星此时高度角较大也无法用高度角随机模型反映观测值质量，这时载噪比与信号强度随机模型更能体现观测值质量。从图1与表2的结果可知，载噪比、信号强度二者的定位结果从总体来看大致相同，在无载噪比数据时，可用信号强度随机模型替代[11]。

2.2 实验二

本次实验数据来自某工程测量项目，基准站架设于地基稳固的某楼顶，流动站位于某主干道旁，两站均无遮挡，测站环境良好，基准站与流动站接收机均为M300 Pro型商用北斗接收机。基准站与流动站接收机仪器设置采样率为1 s，卫星高度角为10°，基线长度为1 099.4 m，该基准站与流动站高差为25.69 m。采用1 000个历元数据参与解算，双频数据选择B1I、B3I，解算策略同实验一。定位结果如图2所示，内符合精度如表3所示。

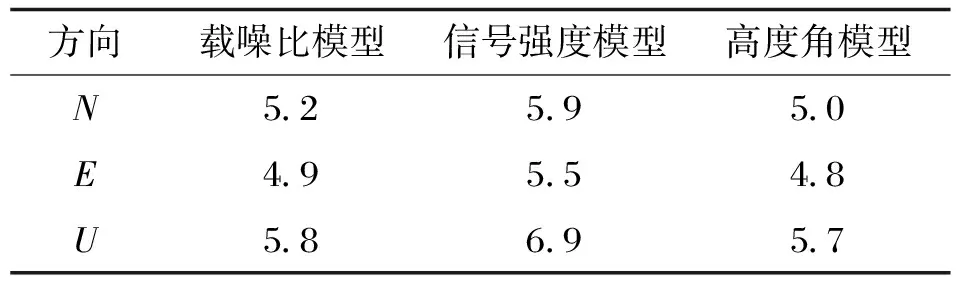
表3 流动站坐标内符合精度统计表/mm

由图2与表3数据可知，这三种随机模型定位结果均较为平滑，其中高程方向定位结果与北方向、东方向定位结果在内符合精度数值上相差较小。其中高度角模型在三个方向的定位结果均优于其余两个随机模型，如高度角模型定位精度北方向、东方向、高程方向分别为5.0、4.8、5.7，均优于载噪比模型和信号强度模型，这归功于两测站之间高差为25.69 m。当组成双差方程时，无法通过双差方法将大气延迟误差消除掉，高差越大残余的大气延迟误差越大，高度角模型可在解算双差方程时，通过高度角这一函数调整权值来削弱残余的大气延迟对定位的影响。

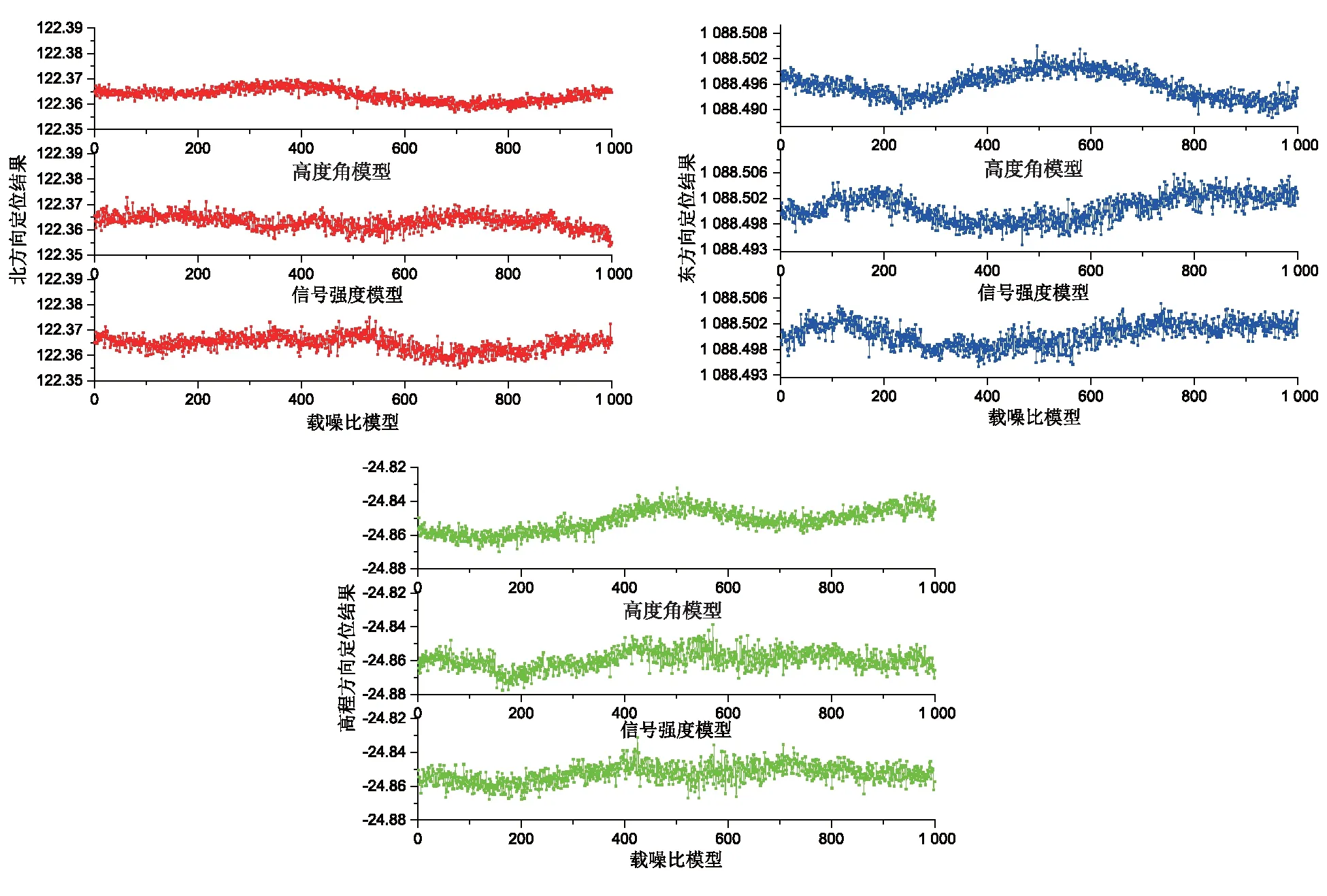
图2 流动站依据不同随机模型获取的坐标值

3 结 论

本文通过基线长度不同、高差不同的两组实验数据，将等权模型、高度角模型、信号强度模型、载噪比模型在Track模块中实现编程并对数据进行处理，以两组具有代表性的实测数据分析了这四种随机模型的应用条件，总结如下：

(1)等权随机模型是一种理想的、简单的随机模型，本文建议在北斗数据处理中采用精度较为优良的载噪比模型、信号强度模型和高度角模型，尽量不要使用等权模型，推荐根据不同情况使用这三种模型；

(2)当基准站与流动站之间高差较大时，推荐使用高度角随机模型，因为该模型能更加有效地减弱大气延迟的影响，定位结果优于其他三种随机模型；

(3)载噪比随机模型、信号强度随机模型定位结果大致相同，信号强度模型可适当代替载噪比随机模型，特别是无载噪比时。