径向孔形状对针栓式喷注器液膜下漏率的影响
王凯,雷凡培,杨岸龙,杨宝娥,周立新
1. 西安航天动力研究所 液体火箭发动机技术重点实验室, 西安 710100
2. 中国船舶工业集团有限公司,北京 100044
近年来使用针栓式喷注器的针栓式发动机成为实现航天器垂直软着陆的一大技术热点和亮点,这是实现运载器重复使用和外行星探索的关键[1],也成为实现低成本、可重复使用运载火箭回收的优选方案之一。
针栓式发动机经过五六十年的研究与发展,已取得了丰硕的工程成果,如著名的阿波罗登月舱下降发动机(LMDE)[2-3]、SpaceX公司的Merlin 1D系列发动机[4-5]以及中国的月球探测器CE-3用的7 500 N针栓式发动机。然而与工程研制的辉煌成就相比,目前针栓式喷注器工作特性的理论研究尚不足,许多机理尚不清楚,相关的研究主要集中于喷雾与燃烧特性研究,例如Ninish等[6]等开展了不同工况下测量雾化角和液滴粒径的试验研究及理论预测,Kim[7]和Sakaki[8]等分别开展了喷注单元的点火特性和燃烧特性试验研究。在针栓式发动机性能提升的过程中,通常通过提高阻塞率来提高燃烧性能,然而往往面临最突出的问题之一就是针栓头烧蚀。在不对针栓头采取额外热防护措施的前提下,通过提高阻塞率提升性能似乎与针栓头的热防护问题是一对矛盾。工程上希望在不降低燃烧性能的前提下,通过采取一定的有效措施达到针栓头的热防护。
目前工程上使用较多的有效方法主要有2种:一种是被动热防护,即针栓头采用如铌钨合金等耐高温的材料制成或者喷涂耐高温抗氧化涂层,然而受材料极限温度限制,单独使用该方式多数情况下仍难以抵抗高热流的冲刷烧蚀。另一种是主动热防护,即通过在针栓头上开孔,将中心一路的推进剂从头部喷出实现主动冷却。为了促使喷出的推进剂能较好雾化,常采用的主动冷却孔形式有直流小孔[9]、自击式喷嘴[10]、小离心式喷嘴[11]等。这种主动冷却方式本质上通过改善流强与混合比分布的方法取得良好的热防护效果。然而主动冷却额外使用了一种推进剂,会降低总体燃烧效率,且难以适应大范围变推要求。这是因为在变推力工况下,主动冷却孔面积不可调,与变推力工况下推进剂主路喷注面积可调不匹配,导致低工况下主动冷却孔路分配的流量占比显著增大,对应的燃烧效率也明显降低,且变比越大,低工况下这种效应越显著。低工况下主动冷却路流量占比可超过30%左右。Vasques和Haidn在研究LOX/LCH4针栓喷注器时用中心氧化剂路10%的流量主动冷却,实现了固定结构工况下针栓头的有效热防护[9]。
经过上述分析可见,主动冷却方式比较适用于固定推力或推力变比不大的情况,可以达到良好的针栓头防护效果,而不太适用于大范围变推力针栓喷注器,故主动冷却方式不能完全满足工程上的需求,即在不降低燃烧性能的前提下,达到针栓头的热防护;然而工程上希望在不降低燃烧效率的前提下,达到针栓头的热防护,即使在大范围变推力的工况下,燃烧效率也不会显著降低。
为了解决上述问题,本研究打算通过合理改变或组织喷雾过程来改善针栓头附近的热环境,从而满足工程需求。LMDE未采用主动冷却,表明依靠合理设计组织喷雾场的方案是可行的。通过合理改变或组织喷雾过程来改善针栓头附近热环境的想法其实源于针栓式喷注器喷雾场结构特征。针栓式喷注器是通过径向液束与轴向环形液膜呈90°垂直撞击,从而使推进剂进行雾化混合[12-13],如图1所示。针栓式喷注器的针栓头伸入燃烧室,位于形成的大喷雾锥结构中心。燃烧状态下针栓头下游流场中存在的大回流区会携带大量热燃气回流至针栓头附近。如果设计不合适,很容易造成针栓头烧蚀。根据前期对针栓喷注器喷雾场的研究,发现轴向环形液膜与径向液束撞击后绕径向液束形成分叉流动[14],从而形成一定的液膜下漏流量。合理地设计并利用这部分下漏流量可达到与主动冷却孔类似的效果,却不用额外消耗推进剂,且在变工况过程中,下漏流量也会随着主路推进剂一起调节变化,故具有较好的大范围变推力流量匹配特性。合理地设计下漏流量,不仅可增加针栓头附近的流强分布,将回流区推离针栓头一定距离,减弱热燃气回流强度;同时还可改变针栓头下游区域混合比分布,使其偏离当量混合比,从而降低该区域燃烧场的温度。
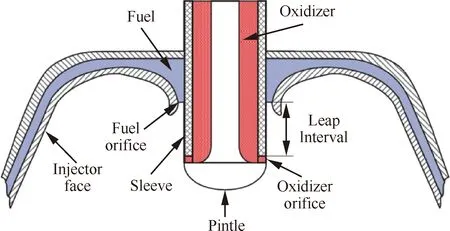
图1 针栓式喷注器原理图
合理设计下漏流量的关键在于预估并控制其大小。如果下漏流量偏小,仍然容易引起针栓头烧蚀;如果下漏流量偏大,过多的液膜下漏又会引起雾化混合效果变差,影响燃烧效率。因此,在设计针栓喷注器时,合理设计并准确预估下漏流量占原轴向液膜流量的比例(即下漏率)是研究如何提高针栓头抗烧蚀能力的关键。
针对以上问题,本文以准确预估下漏率为切入点,以平面针栓多喷注单元为研究对象,基于前期针对径向圆孔液束建立的考虑液膜液束变形和多喷注单元间相互影响的下漏率模型,首先通过类比分析,理论推导建立径向矩形孔的膜束各自相对变形模型;再推导建立对应的不同高宽比矩形孔的下漏率模型;然后通过试验及数值仿真对不同径向孔形状的下漏率模型进行验证;最后通过对比分析为径向孔形状选择给出合理建议,并给出模型中的常系数供工程设计预估使用,这对从设计初期就考虑针栓头的热防护问题具有重要的指导意义。
1 数值物理模型
1.1 数值方法
1.1.1 流动控制方程
对于喷雾计算过程来说,数值求解气液2种流体均采用的是不可压缩的、变密度的、带有表面张力的Navier-Stokes方程[15]。具体的控制方程为
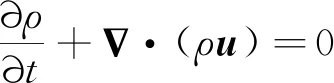
(1)
动量方程:
(2)
式中:u=(u,v,w)为流体速度;ρ=ρ(x,t)为流体密度;p=p(x,t)为流场中的压力;τ为黏性应力;σ为表面张力系数;δ(x-x′)为Dirac函数,表示表面张力项集中在界面上;κ和n分别为界面的曲率和法向方向;S(t)表示气液相界面。
另外,本文计算主要关注撞击变形及流动过程,采用2种液体和气体分别追踪的分三相Volume of Fluid(VOF)方法。为了分别识别两路液体的变形运动过程,定义了2种液相体积分数来进行2种推进剂的分别追踪计算,分别为液相1体积分数α1和液相2体积分数α2,对应得到的流体密度和动力黏性系数为
ρ=α1ρl1+α2ρl2+(1-α1-α2)ρg
(3)
μ=α1μl1+α2μl2+(1-α1-α2)μg
(4)
式中:ρl1、ρl2和μl1、μl2分别为液相1和液相2的密度和黏度;ρg和μg分别为气相的密度和黏度。
每一相液体对应的体积分数输运方程为
(5)
1.1.2 气液相界面捕捉及表面张力
计算中气液相界面捕捉采用两相流计算中最为常用的VOF方法,该方法具有较好的守恒特性[16],且气液相界面重构精度较高[17]。液体表面张力的计算采用常用的CSF(Continuum Surface Force)方法,该方法是通过在式(2)的动量方程中加入体积力源项来实现[15]。表面张力的计算式为
(6)
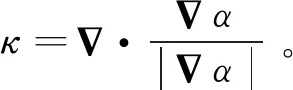
1.2 计算模型
在针栓式喷注器下漏率的计算模型中选取3个 完全相同的喷注单元作为研究对象,计算域模型如图2所示。两路液体均采用速度入口边界,计算域两侧为对称面边界,计算中壁面均为无滑移边界,其余面为压力出口边界,背压设置为大气环境。计算中选用两路介质均为水,环境气体为空气,采用Fluent中标准的k-ε湍流模型和标准壁面函数[15]。计算域网格划分采用880万全结构化网格,对撞击点及液膜流动区域进行加密处理,最小网格尺寸达到约30 μm,时间步长达到10-4ms量级,这样可以快速收敛,进而更好地捕捉相界面和统计下漏流量。
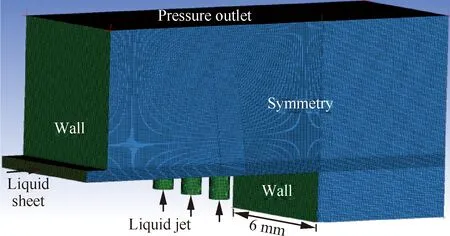
图2 多喷注单元计算域模型
2 多喷注单元试验装置及试验测量系统
2.1 多喷注单元试验装置
冷态试验的喷注器设计借用了文献[8]中平面针栓式喷注单元的设计理念,采用喷嘴结构可更换的方案设计了平面针栓多喷注单元试验装置。平面针栓多喷注单元由一个可更换的液膜生成部分和一个可更换的多液束生成部分组成,试验件如图3所示。液膜生成部分可以产生一定厚度的平面液膜来模拟轴向液膜路,平面液膜足够宽,设计中多孔喷注单元选取液膜宽度为20 mm;液束生成部分可以产生一定孔型型面和一定尺寸的射流。试验中液膜和液束两路单独供应,通过分别改变液膜和液束两路流量及更换不同结构尺寸的液膜和液束构件,从而形成不同的工况[18]。另外,原则上采用3个喷注孔即可模拟多喷注单元间的相互影响,然而试验件中液束构件采用了9个径向孔,这主要是为了增加展向宽度,便于下漏流量收集,同时也为了提高试验中流量控制及下漏流量收集测量精度。
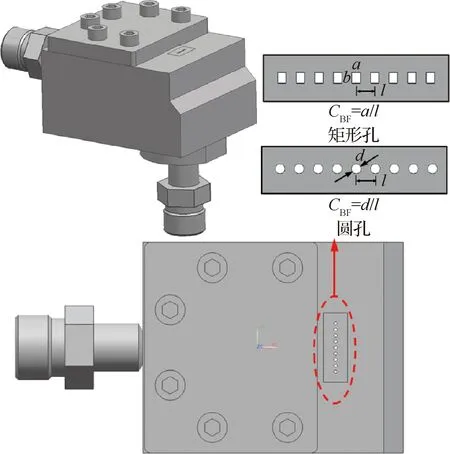
图3 液液平面针栓多喷注单元试验件结构
2.2 试验测量系统
试验系统简图如图4所示,下漏流量采用在喷嘴下方采用容器收集的方案,试验中使用工装严格定位收集容器的位置,具体收集的喷雾场下漏区域与数值仿真统计的方式一致,即与轴向夹角为10°范围内的液体流量,如图5所示。在喷雾场达到稳定状态时,通过收集一定时间的液体进行称重来获得收集的流量。试验中分别对比了收集30、40、50、60、90 s的结果,分析发现收集时间超过50 s以上,换算得到的收集流量相差不多,相对误差5%以内,收集30 s的结果与其有一定差别,故试验中统一选取收集60 s进行试验,且对于每个工况重复收集2~3次,取试验平均值进行统计分析获得下漏流量。
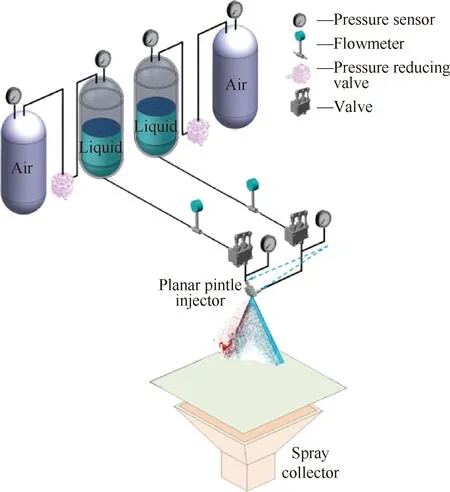
图4 下漏流量收集试验系统
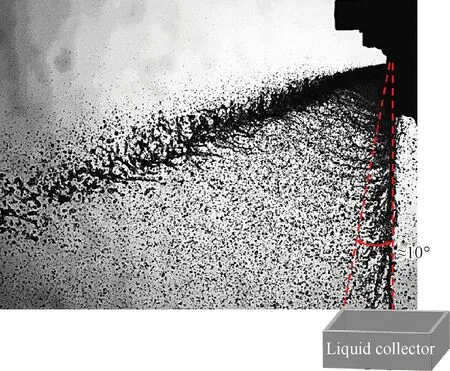
图5 试验结果获取下漏率示意图
2.3 试验数据处理
通过收集一定时间t内的液体,并称重得到其质量为m,然而试验中轴向液膜是具有一定宽度的,边缘处存在无效撞击液膜,直接无法测得有效的下漏流量。假设液膜在整个W=20 mm宽度内均匀,考虑到两侧的边缘效应,统计时通过换算去除两侧的影响,如图6所示,试验件选用9孔也是为了降低边缘效应的影响。于是有效下漏流量为8l+d宽度范围内的流量,换算得到的下漏率计算公式为
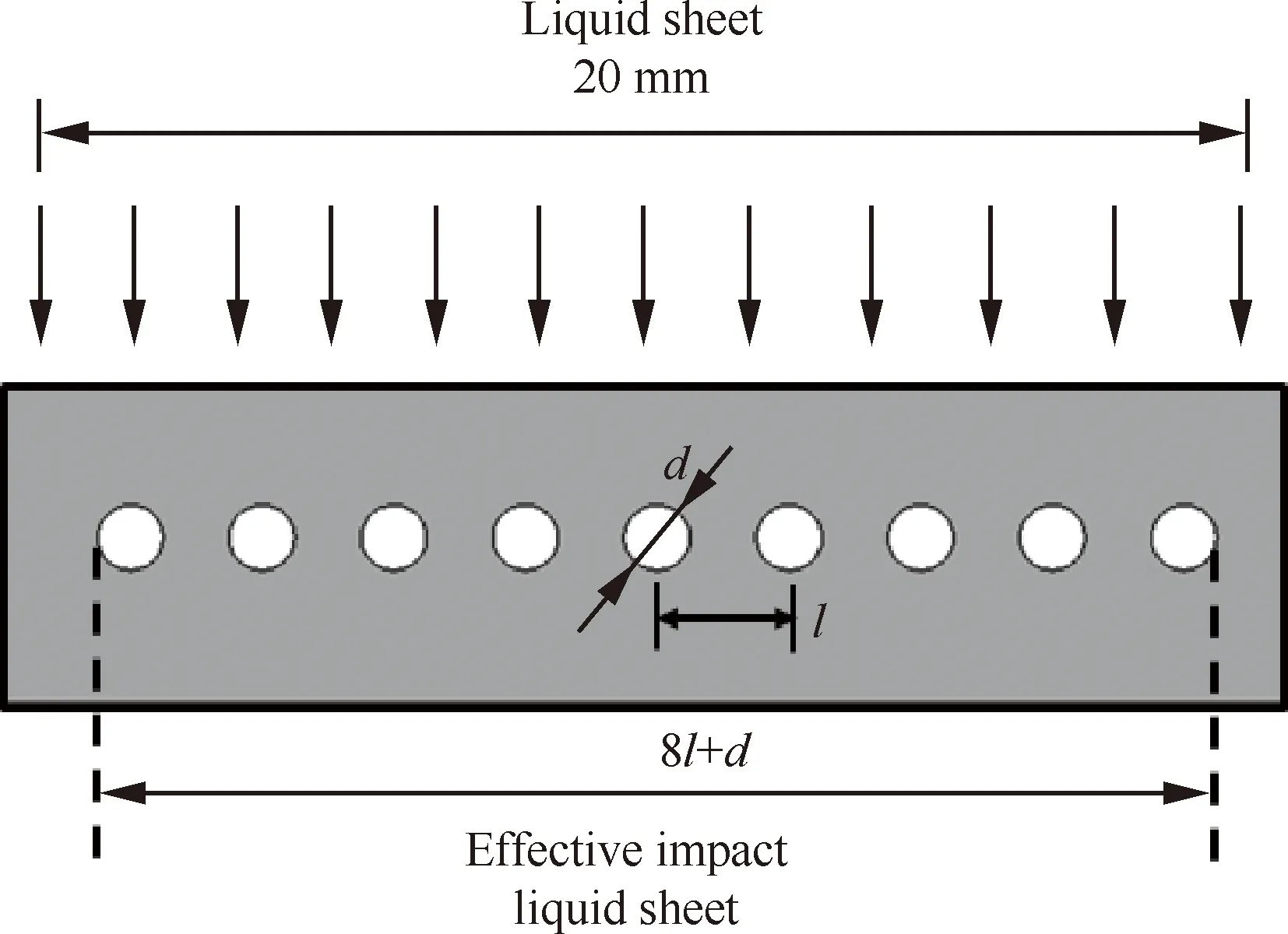
图6 下漏流量换算示意图
(7)
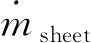
3 理论建模分析
3.1 径向圆形孔的下漏率基本定义及相关分析
对于针栓式喷注器,液膜与液束撞击后部分液膜绕过液束会从相邻液束孔之间下漏,形成液膜下漏流量。下漏过程如图7所示,根据图7中关系可以得到液膜下漏流量为
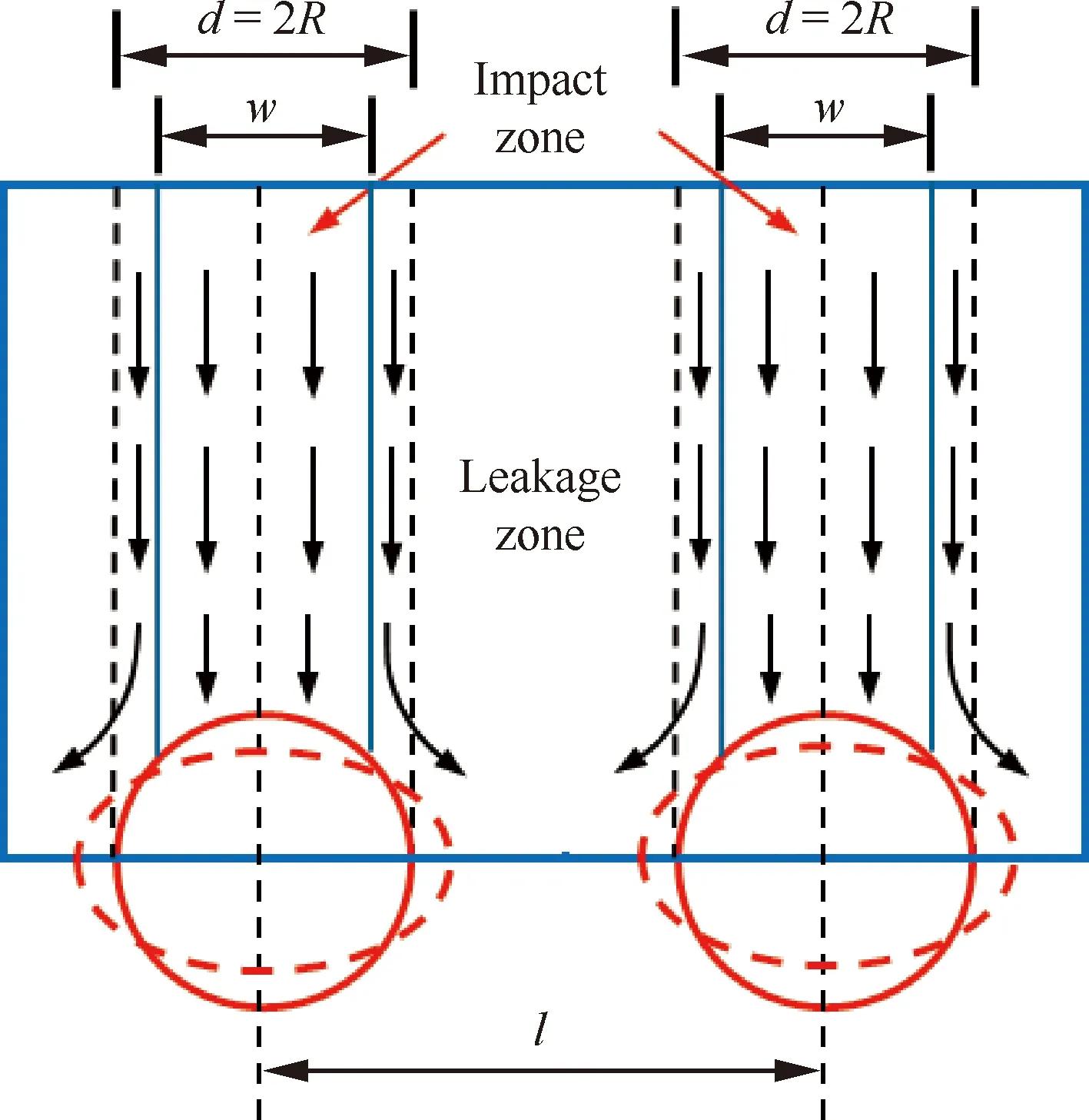
图7 液膜/液束撞击下漏过程示意图
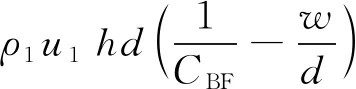
(8)
式中:ρ1为轴向路液体密度;u1为轴向路液膜速度;h为轴向路液膜厚度;w为与液束发生有效撞击的液膜宽度。对应的阻塞率CBF=d/l。
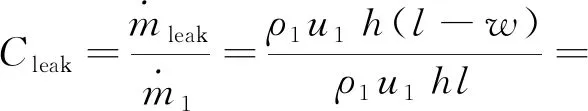
(9)
式(9)是基于液束不变形建立的,实际中液束受撞击后会发生变形,如图7中虚线所示。随着撞击过程中液束的展向变形增大,更多的液膜流量被液束撞击带离轴向,实际液膜下漏流量及下漏率会较式(8)和式(9)预估的偏小,且液束变形越大,偏小程度越大。该影响主要体现在阻塞率上,由于液束的变形,展向宽度增加,实际阻塞率C′BF比几何阻塞率CBF更大。
于是用实际阻塞率替换式(9)中的几何阻塞率可得到考虑液束变形的下漏率预估模型:
(10)
式中:实际阻塞率C′BF=d′/l,d′为液束变形后的展向宽度(即长轴直径)。可以发现,d′/d描述的是液膜/液束撞击过程中液束的变形,w/d描述的是液膜/液束撞击绕流过程中液膜的变形。
从式(10)可以看出下漏率与阻塞率CBF、w/d和d′/d有关。一旦确定了阻塞率CBF和液膜液束相对变形参数(d′/d和w/d),便可预估出实际液膜下漏率。
3.2 径向圆形孔的下漏率建模过程
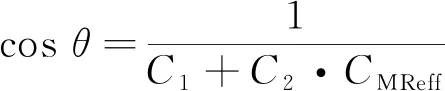
(11)
从式(11)分析可以得出,w/d主要与动量比有关,即w/d=f(CMReff),其在之前研究中已得到试验换算结果及数值仿真结果的验证,具有较好的准确性。另外,采用最小二乘法对试验数据拟合得到了w/d与CMReff的关系式为
(12)
式中:a1为常系数。
通过数值仿真结果发现,液束受到液膜撞击作用后从两侧开始变形,圆截面被压扁,展向宽度逐渐增加,液束的撞击前缘在液膜正压和剪切作用下向下游移动,而后缘在液膜厚度范围内几乎未移动。因此,假设液束根部横截面受到液膜撞击作用后由圆形变成椭圆形,液束后缘位置保持不变,展向宽度d′增加(即为椭圆的长轴),短轴可根据如图8所示的几何关系计算得到为d-h/tanθ,同时可假设液束流速大小保持不变,仅速度方向发生改变。
根据图8的几何关系及质量守恒可得
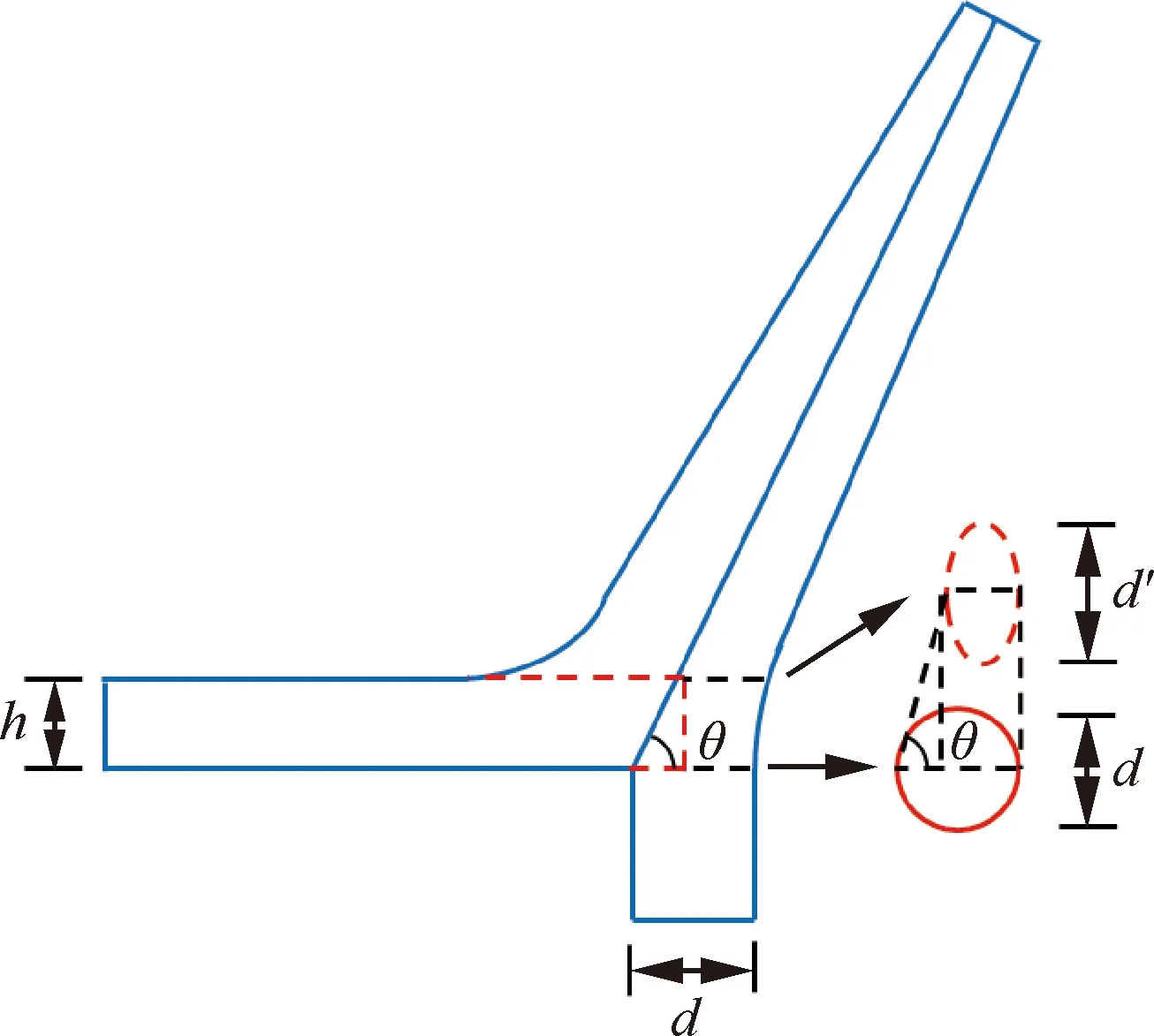
图8 圆形孔液束根部变形过程模型示意图
(13)
式中:θ′=(θ+π/2)/2,表示撞击后液束中心速度方向为前后缘角度的平均值。
由式(13)可得液束的相对变形量为
(14)
实际的液束根部横截面变形后虽然不是严格的椭圆形,与式(14)模型存在一定的差异,式(14)将变形后的横截面当作椭圆处理,低估了变形量d′/d,但式(14)可以近似反映液束的相对变形d′/d与液膜/液束几何特征参数h/d和有效动量比CMReff有关,可以近似地描述d′/d与h/d及CMReff的关系。式(14)也得到了如图9所示的数值仿真结果的验证,从添加流线的体积分数云图上使用GetData软件获取边界,测量获取d′/d的定量数据。
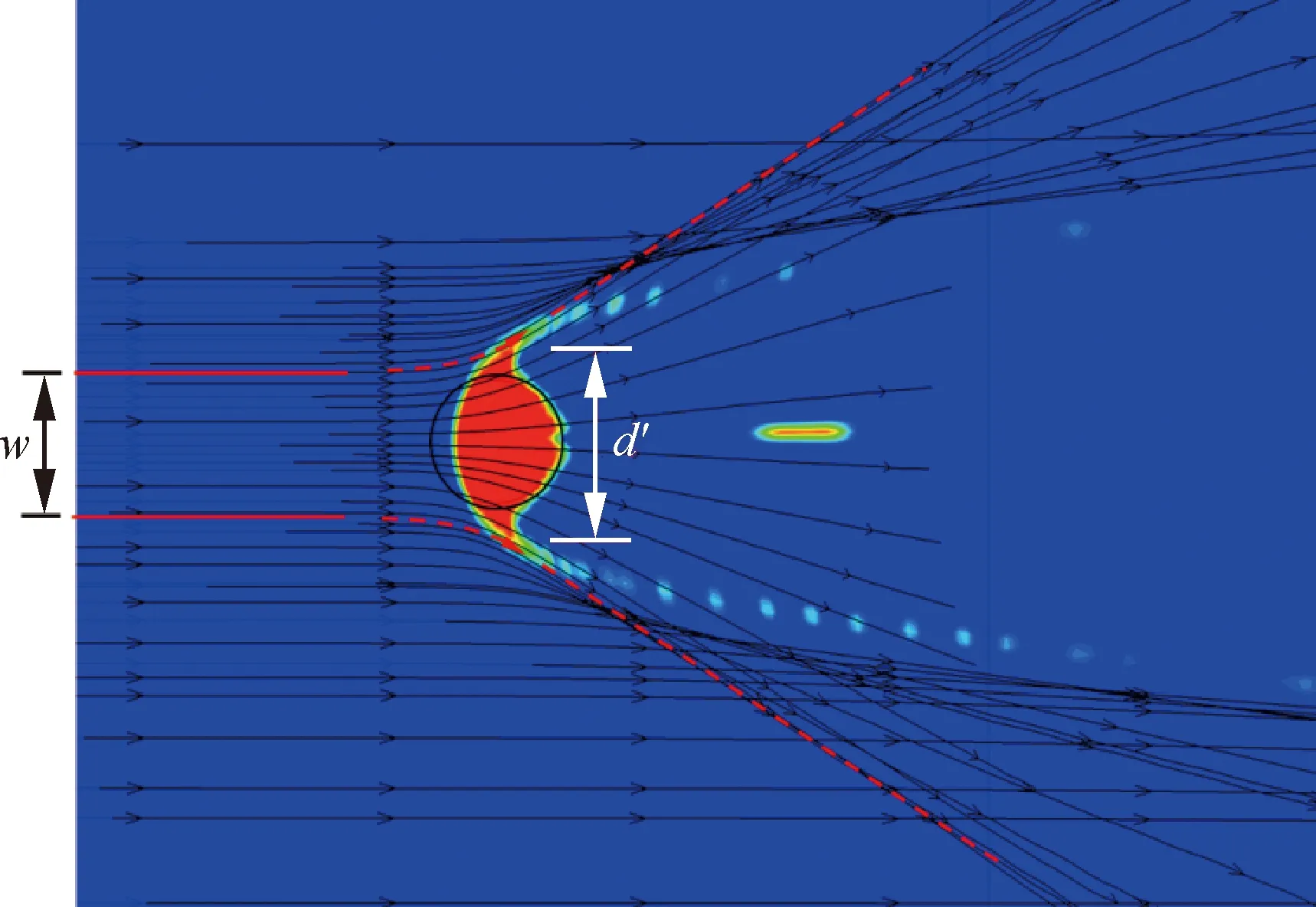
图9 添加流线的体积分数云图
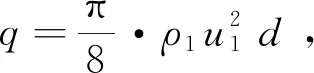
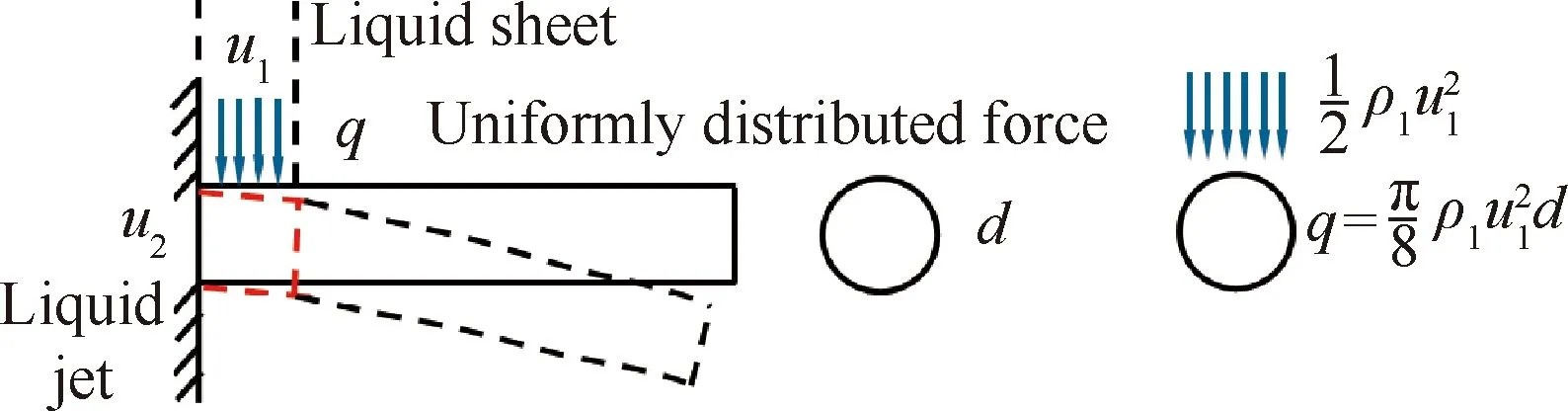
图10 液膜撞击液束根部受力变形分析
(15)
根据式(15)可对有效动量比很小时的情况做一定的修正。
以上述获得的液膜相对变形量式(12)和液束相对变形量式(14)或(15)为基础,将其代入下漏率表达式(10)中,并考虑常系数C0可得
(16)
另外,考虑到相邻喷注单元之间的相互影响,引入相互影响系数来表征实际相互影响下的液束相对变形量与单个单元的比值,并假设其随孔边距(l-d)的增大而增大,取值范围为0~1,即
(17)
相邻多喷注单元之间的相互影响通过式(17)对液束的变形量进行修正,对液膜的变形量修正体现在指数a1中。修正后式(16)变为
Cleak=1-C0·CBF·
(18)
式(18)即为考虑多喷注单元间相互作用的液膜与径向圆形孔液束撞击的下漏率模型。
3.3 径向矩形孔的下漏率建模过程
针对径向孔为矩形的多喷注单元,类比上述径向圆形孔,可得到类似的下漏率模型。液膜相对变形模型不变,只需将式(12)中的圆孔直径d替换为矩形孔的宽度a,则式(12)变为
(19)
同样,假设矩形孔受到液膜撞击作用后横截面仍近似为矩形,仅高宽比发生变化,即变扁,展向宽度a′增加,截面高度减小为b-h/tanθ,高宽比减小,如图11所示。根据几何关系计算可得到液束相对变形模型为
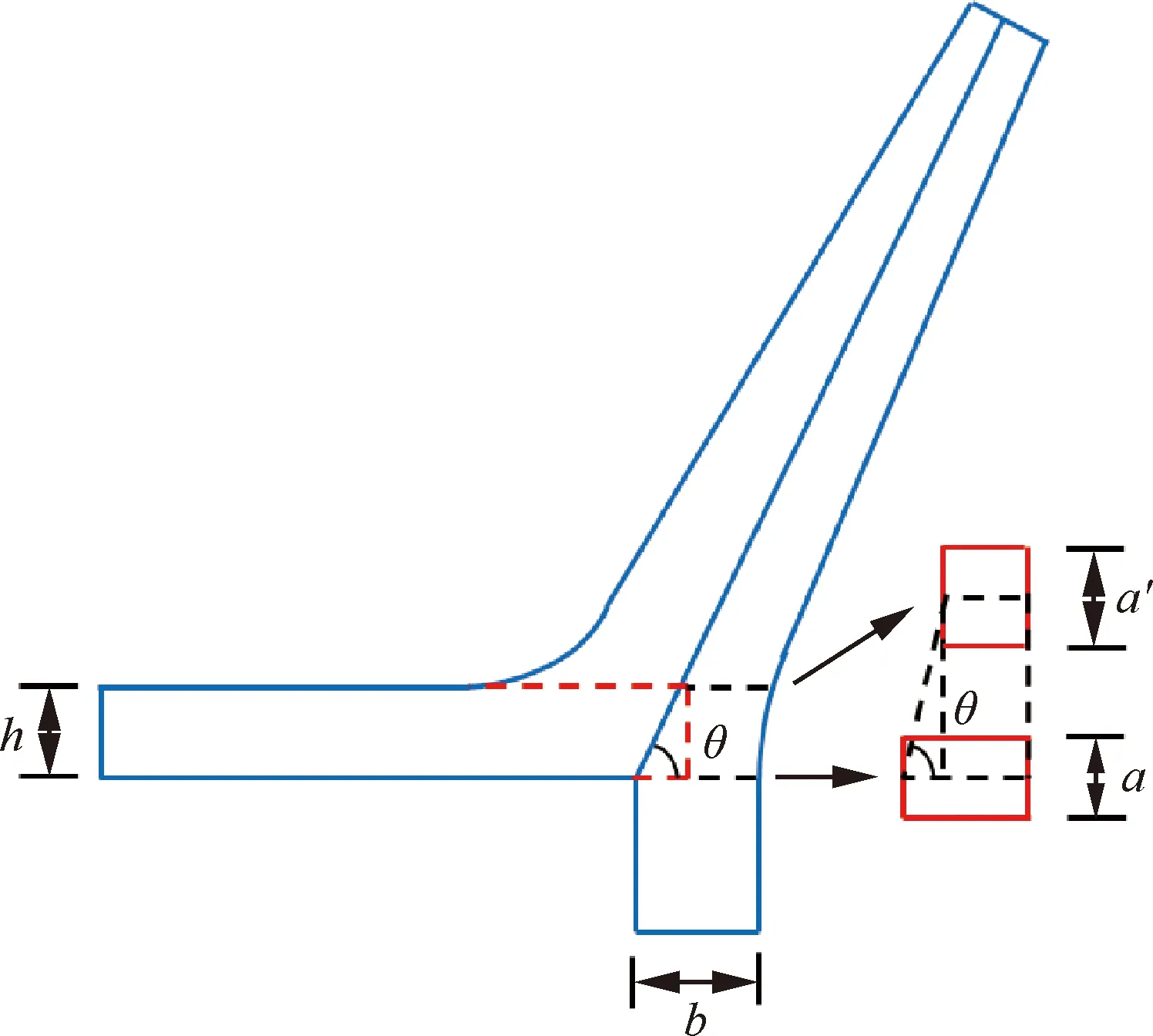
图11 矩形孔液束根部变形过程模型示意图
(20)
采用与径向圆形孔同样的思路,考虑小动量比下液束后缘移动效应的液束相对变形模型为
(21)
考虑多喷注单元间的相互影响后的下漏率模型变为
(22)
式中:阻塞率为CBF=a/l。
另外,液膜与径向矩形孔液束相互作用过程中存在侧边效应的影响,参考文献[6]中对矩形孔绕流侧边效应影响的表征,引入不同高宽比的矩形孔影响系数(1+CRb/a),其中CR为对应的矩形孔系数,将其代入式(22)可得
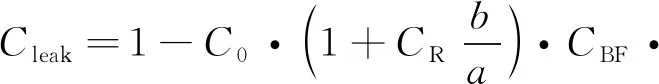
(23)
式(23)即为液膜与矩形孔液束撞击的下漏率模型。
4 模型验证与结果分析
针对径向圆形孔的液膜下漏率模型在之前的研究中已得到有效验证[19],分别对比了2种不同阻塞率结构下下漏率随有效动量比的变化,均吻合较好。另外,在保证相同结构参数和有效动量比下,还对比了3种不同喷射速度下的下漏率,数值仿真、试验结果与理论模型预测值均不随喷射速度绝对值的变化而变化,进一步表明了下漏率理论模型的准确性。然而研究结果表明,径向圆孔的下漏率随着工况的降低会减小,这使得低工况下液膜下漏流量更低,造成低工况下热防护风险增高,因此径向圆孔似乎不太适合工况大范围变化下的需求。
下面主要针对上述径向矩形孔的下漏率模型开展不同有效动量比下的数值仿真算例验证,研究对象为3种不同高宽比的矩形孔,孔的横截面积均与d=1.0 mm的径向圆孔相等。轴向液膜厚度为h=0.45 mm,径向矩形液束孔宽度和高度分别取a=0.9 mm和b=0.9 mm、a=0.704 mm和b=1.15 mm、a=1.15 mm和b=0.704 mm,对应的高宽比b/a分别为1.0、1.63和0.61。相邻孔中心间距均选取为l=2.0 mm,此时对应的阻塞率分别为CBF=0.45,CBF=0.35和CBF=0.575,具体的算例参数如表1所示,径向圆孔对应的算例参数如表2所示。
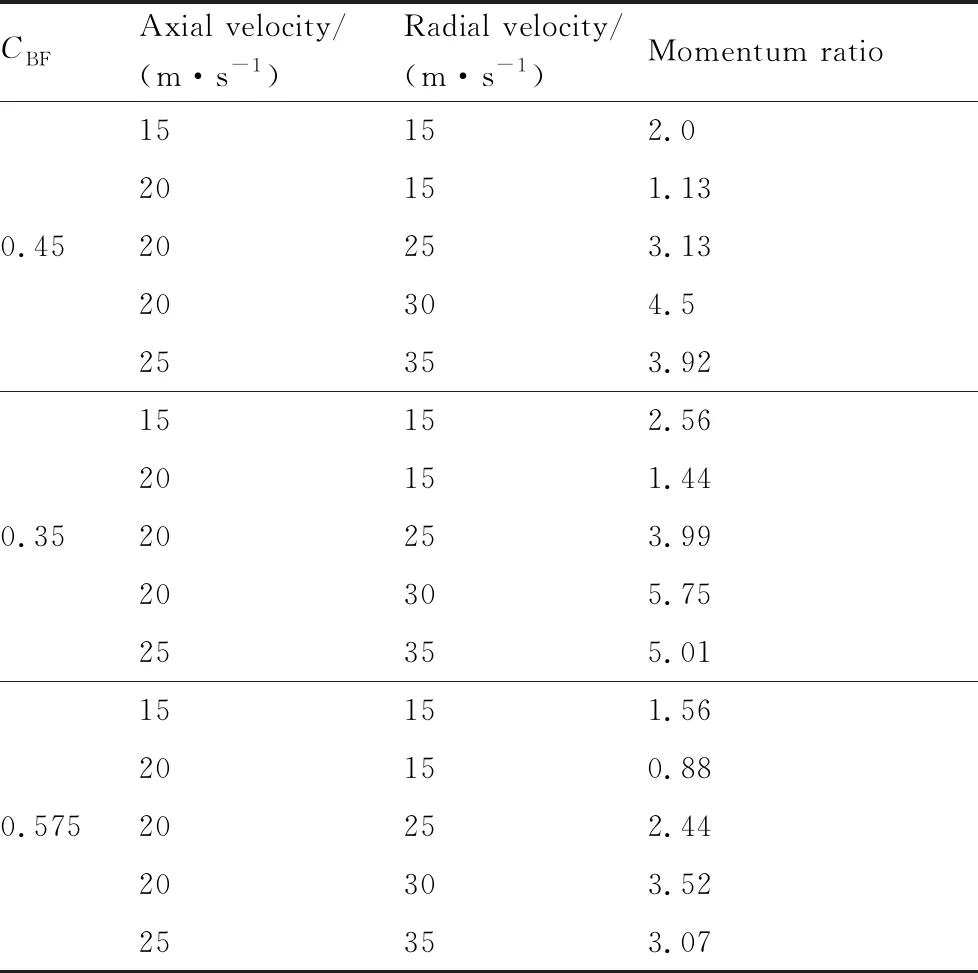
表1 3种不同高宽比的矩形孔在不同有效动量比下的算例参数
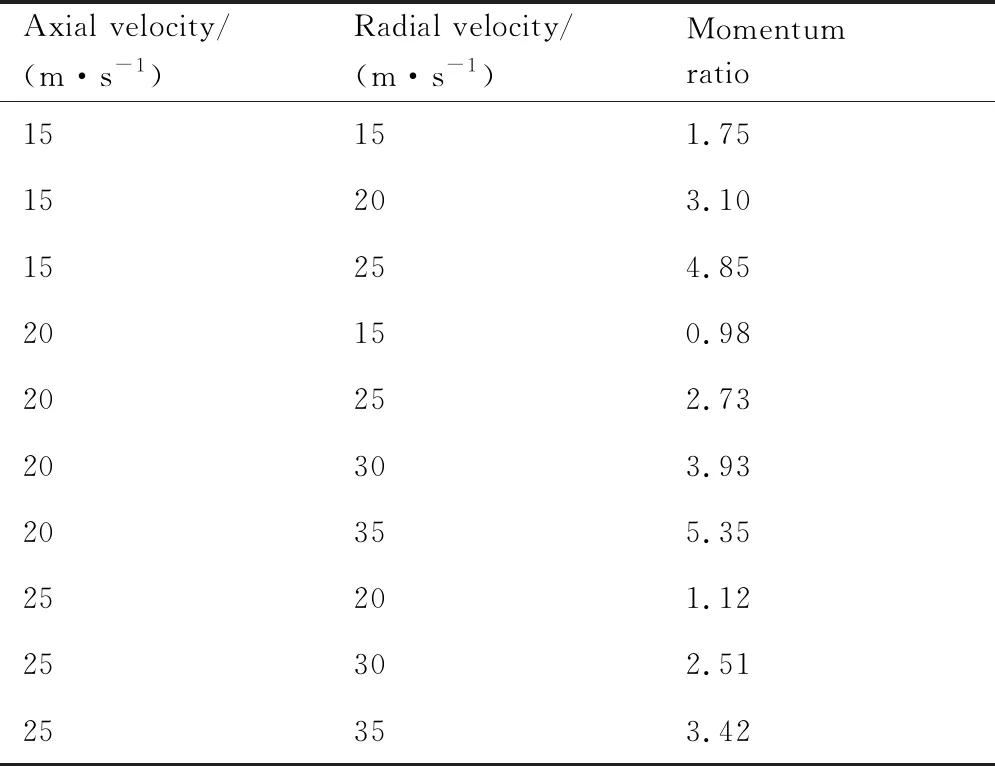
表2 径向圆孔在不同动量比下的工况参数表(CBF=0.5)
与径向圆孔时一样,根据数值仿真结果获取下漏流量及下漏率的示意图如图12所示,提取与轴向夹角为10°范围内的轴向液膜流量认为是下漏流量。为了减小采样误差,分别选择6个横截面位置作为采样截面,即x0、x1、x2、x3、x4和x5,其中x0为径向矩形孔液束中心所在截面位置,其余位置依次间隔1 mm。(注:此处选取10°夹角范围与径向圆形孔是一致的,这样可以保证定量对比评估的准确性,这也是根据液膜下漏后的流场结构确定,且这样选取可使得6个采样截面的下漏流量接近,也与x0截面的下漏流量参考值相近)。试验收集的喷雾场区域与数值仿真完全一致,详见前文2.2节,通过式(7)统计分析得到对应的下漏率。
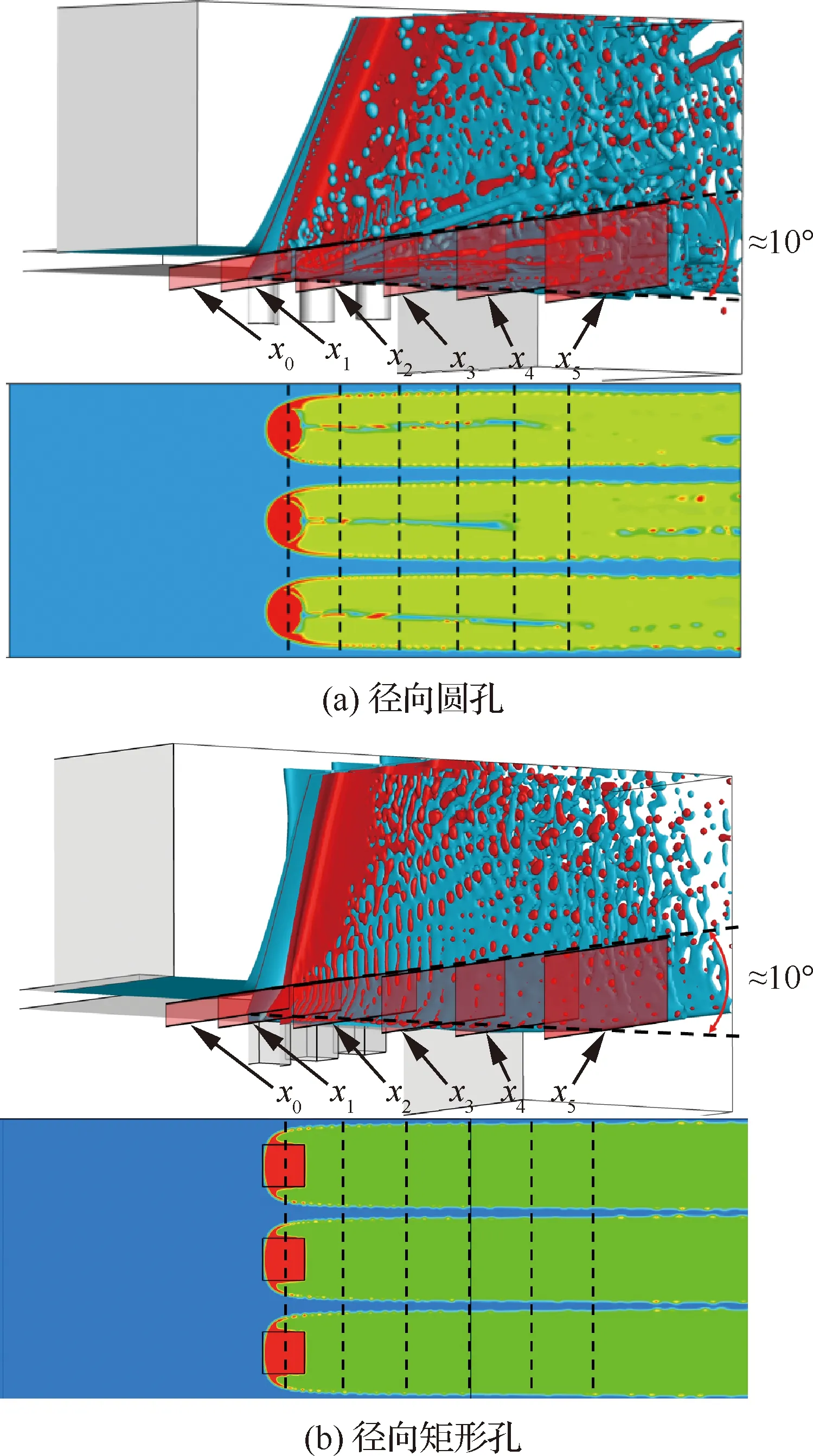
图12 数值仿真结果获取下漏率示意图
获取3种不同高宽比矩形孔的下漏率随有效动量比的变化如图13所示,分别对比了x0截面的下漏率、6个截面的平均下漏率、试验测量下漏率及式(23)考虑喷注单元间相互影响模型的下漏率。式(23)模型中系数根据数值仿真结果拟合获得,从图13中可以发现数值仿真及试验结果与理论模型预测值吻合较好,下漏率模型具有较高的准确性。同时可以发现3种不同高宽比情况下的下漏率均显著小于几何下漏率,即1-CBF。在所研究的工况下,下漏率均小于0.35。另外,下漏率随有效动量比增大而增大的趋势均较缓,特别是有效动量比大于2~3时。与如图14所示的相同横截面积的d=1.0 mm径向圆孔相比,下漏率显著减小,表明在孔心间距一定时,对于相同的径向孔面积,矩形孔的下漏率小于圆孔的。从模型中的系数a1变小及C0(1+CRb/a)变大也可以看出,这正好说明矩形孔时的轴向液膜绕流效应相对较弱,液膜相对变形量随有效动量比变化范围较小,对应的实际阻塞率和实际下漏率随有效动量比变化也较平缓。然而由于不同高宽比的矩形孔存在侧边效应,故高宽比b/a越大,几何阻塞率越小,轴向液膜被带到径向的流量越小,使得下漏率越大。另外,通过径向圆孔与矩形孔的对比,也可以推论得到矩形孔前缘两侧倒角可使得下漏率在原基础上增大。
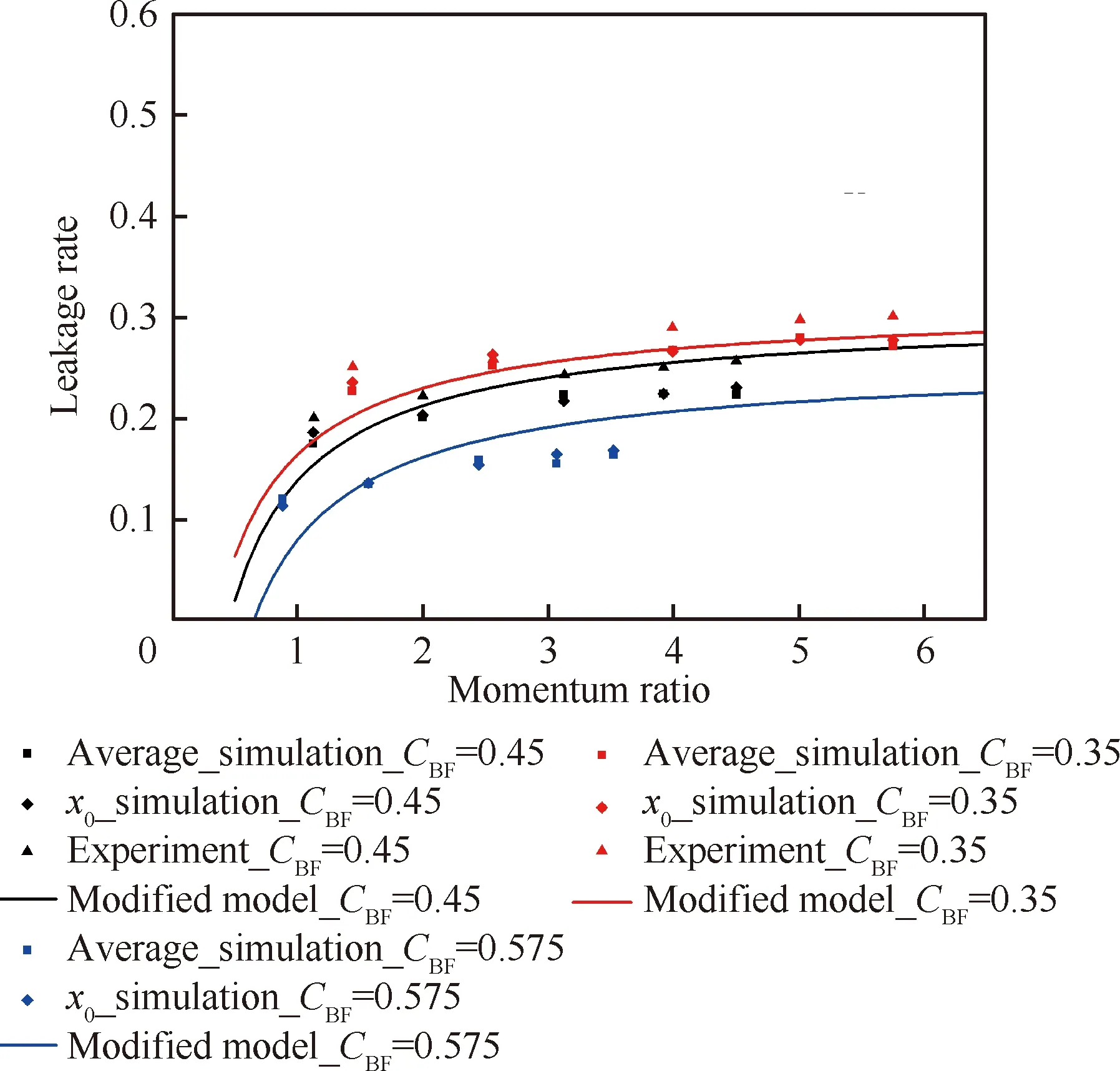
图13 不同高宽比矩形孔的下漏率随有效动量比的变化
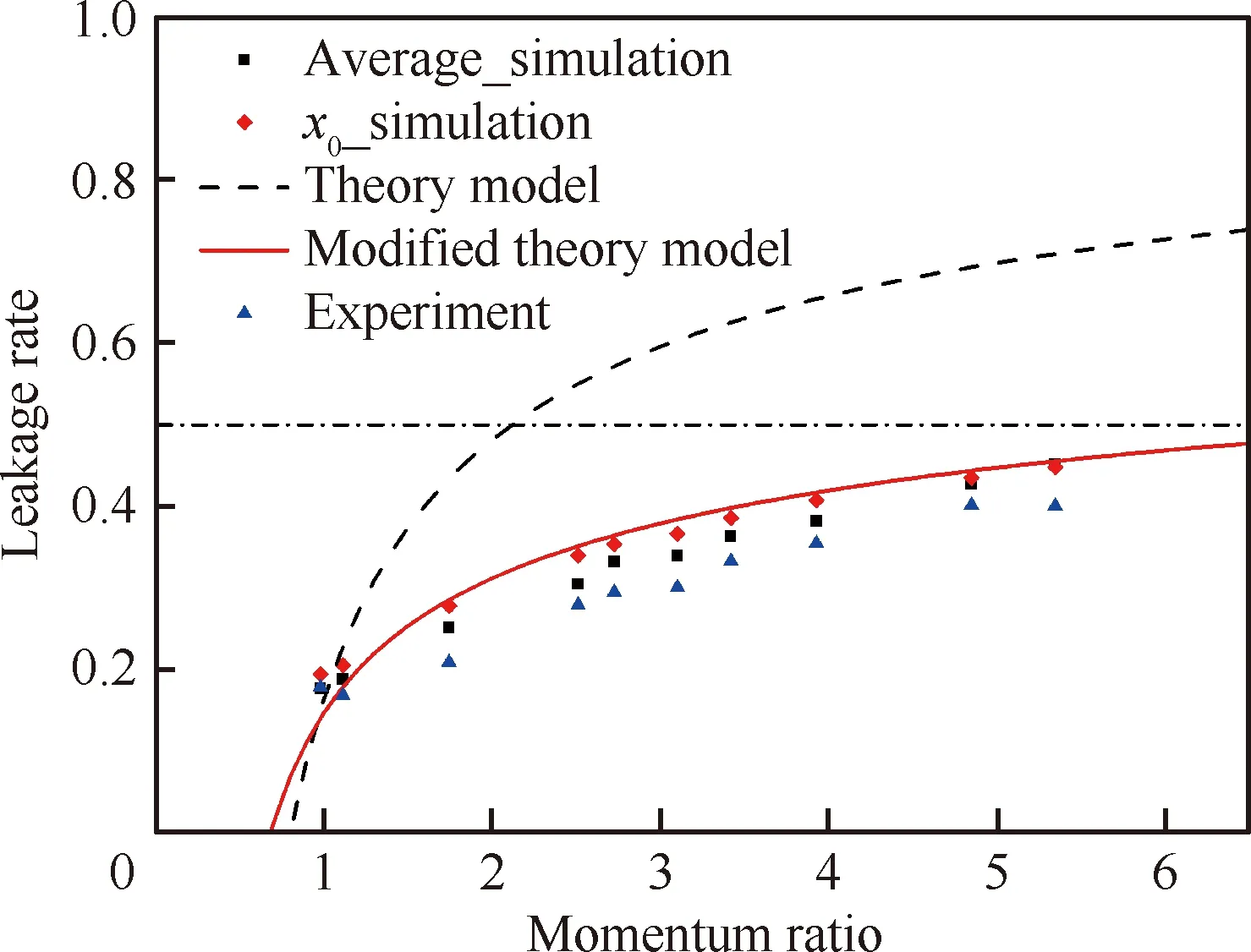
图14 径向圆孔下漏率随有效动量比的变化规律(CBF=0.5)
综上所述,可以发现在径向孔横截面积及流量等工况参数完全一样的情况下,径向孔的形状对下漏率有显著的影响,矩形孔的下漏率低于圆形孔的;矩形孔的高宽比越大,下漏率越大。在实际应用中选择矩形孔更有利于控制下漏率,并可通过改变高宽比来控制下漏率;同时在变工况调节过程中,只要保证h/b的值基本不变,无论改变喷注面积还是喷注压降,下漏率均保持变化不大,下漏流量也会随着主路推进剂一起调节变化,故具有较好的大范围变推力流量匹配特性。
5 结 论
为了研究径向孔形状对针栓式喷注器液膜下漏率的影响并对其进行准确预估,考虑液膜液束各自变形和多喷注单元间相互影响推导建立了径向圆形孔和不同高宽比矩形孔的实际下漏率模型,并通过试验及数值仿真对模型进行了验证分析。
1) 通过类比分析,基于径向圆孔相对变形模型,推导建立了径向矩形孔的相对变形模型及下漏率模型,并考虑了不同高宽比的矩形孔的绕流侧边效应,得到的理论预估结果与数值仿真及试验结果吻合较好,表明针对矩形孔建立的相对变形模型及下漏率模型具有较好的准确性。
2) 针对矩形孔的研究表明,下漏率除了与几何阻塞率、有效动量比及h/b有关外,还与高宽比有关。3种不同高宽比情况下的下漏率均显著小于几何下漏率,即1-CBF;高宽比b/a越大,下漏率越大。下漏率随有效动量比增大而增大的趋势均较平缓;且下漏率显著低于相同横截面积的径向圆孔的。
3) 综合分析径向圆孔和3种不同高宽比矩形孔的结果发现,在工况参数完全相同的情况下,径向孔的形状对下漏率有显著的影响。在实际中选择矩形孔更有利于控制下漏率,并可通过改变高宽比控制下漏率;同时在变工况过程中,下漏流量也会随着主路推进剂一起调节变化,保持下漏率变化不大,故具有较好的大范围变推力流量匹配特性。

